文档内容
{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}学年第二学期三市联合期末检测
2023—2024
高一数学参考答案
.【答案】
1 D
【解析】 根据题意 集合A满足 x x 集合B满足y x -1
, - +2>0⇔ <2, =e +1>1,
所以A B x x .
∩ = 1< <2
.【答案】
2 C
【解析】 根据题意z 2023 2022 .
,=2i -i =1-2i
.【答案】
3 B
【解析】 根据题意 利用分层抽样方法可知 人样本也应该按照 来分配
, ,20 5∶2∶3 ,
所以抽取的职工中属于青年的职工人数为 人.
6
.【答案】
4 C
【解析】 根据线面平行的判定定理可得 选项 正确
, A ;
根据线面垂直的性质 可得两条直线平行 选项 正确
, , B ;
由于不清楚直线a是否在平面α上 选项 错误
, C ;
由于a αaβ 所以存在b' α使得b'b又因为b β 所以b'β
⊂ ,∥ , ⊂ , ∥ , ⊂ , ∥ ,
ab为两条异面直线 因此a b' A 所以αβ 选项 正确.
, , ∩ = , ∥ , D
.【答案】
5 C
T
【解析】 根据题意 AB π T 所以2π ω
, = = ⇔ =π, ω=π⇔ =2,
4 4
因为fx x φ 过点 2π
()=2cos(2 + ) ,0 ,
3
所以f2π 4π φ 4π φ 3 k φ π k
=2cos + =0⇔ + = π+2π⇔ = +2π,
3 3 3 2 6
又因为 φ 所以 φ π 所以fx x π f π 2π π .
<π, = , ()=2cos2 + ⇔ =2cos + =-3
6 6 3 3 6
.【答案】
6 D
c b c
【解析】 根据题意 利用正弦定理 33 C
, C= B= =6⇔sin = ,
sin sin 3 6
2
c
该方程在C 2π 有两个解 所以 3 c .
∈0, , ∈ ,1 ⇔ ∈ 33,6
3 6 2
.【答案】
7 C
【解析】 若事件A与B互斥 则PA B . . . 选项 错误
, ( + )=03+06=09, A ;
若PA B . . 则 AB一定有公共部分 选项 错误
( + )=08<09, , , B ;
若事件A与B相互独立 所以A与B相互独立
, ,
则PAB PA PB . . . 选项 正确
( )= ( )· ( )=07×04=028, C ;
若PAB . PAPB 所以事件A与B相互独立 则不互斥 选项 错误.
( )=012= ( ), , , D
.【答案】
8 A
【解析】 根据题意 设点O到平面ABC的距离为h
, ,
利用等体积法V 1 1 1 h 1 3 h
,O - ABC = ×3× ×3×3= × × × ×32×32⇔ =3,
3 2 3 2 2
高一数学参考答案 第 页(共 页)
1 5
{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}取点D为等边三角形ABC的中心 则OD
, =3,
分析可得点P的轨迹为圆 该圆的半径为r2 OP2 OD2
, = - =6-3=3,
所以点P的轨迹为以D为圆心 以 为半径的圆 此圆在三角形ABC内部只有部分轨迹
, 3 , ,
分析可得 此圆在三角形ABC内部的轨迹占整个圆的1
, ,
4
所以点P的轨迹长度为1 3π.
×2π×3=
4 2
.【答案】
9 BC
【解析】 若z为虚数a2 a a 且a 选项 错误
, +2 -3≠0⇔ ≠1 ≠-3, A ;
a
若复平面内表示复数z的点位于第二象限 则 -1<0 a 选项 正确
, a2 a ⇒ <-3, B ;
+2 -3>0
若z 所以z为实数a2 a a 或a
>-2, , +2 -3=0⇔ =1 =-3,
当a 时z 满足题意 当a 时z 不满足题意 选项 正确
=1 ,=0, , =-3 ,=-4, , C ;
若a 且a 则z是虚数 则z2 z2 选项 错误.
≠1 ≠-3, , ≠ , D
.【答案】
10 AC
【解析】 a b ab ab 1 选项 正确
1= +2 ≥2 2 ⇔ ≤ , A ;
8
a2
+4
b2 a
+2
b2
a2 b2 1 选项 错误
≥ ⇔ +4 ≥ , B ;
2 2 2
b a
8 1 a b 16 选项 正确
a+b +2 =8+2+a +b≥18, C ;
因为a b b a 又因为ab为正数 a
+2 =1⇔2 =1- , , 0< <1,
所以a2 b a2 a a 2 选项 错误.
+4 = +2-2 = -1 +1>1, D
.【答案】
11 BCD
【解析】 分析可知A B DM不共面 选项 错误
,1,1, , , A ;
几何体M ABBA可以放到一个 的长方体内
- 1 1 2×2×1 ,
所以几何体M ABBA的外接球与 长方体的外接球相同
- 1 1 2×2×1 ,
该外接球的直径为
2 2 2
2+2+1 =3,
所以该外接球的半径为3
,
2
该外接球的体积为V 4 3 3 9 选项 正确
= ×π× = π, B ;
3 2 2
根据题意 取点NQ分别为AD AA的中点 分析可得平面MNQ 平面ACD
, , 1 1,1 , ∥ 1,
所以点P的轨迹为NQ NQ 选项 正确
, =2, C ;
在正方体的左边作一个相同的正方体
,
利用对称性可得 MP PC 的最小值为 2 2 2 选项 正确.
, + 1 4+2+1 = 21, D
高一数学参考答案 第 页(共 页)
2 5
{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}.【答案】
12 43
【解析】 根据题意可得 设扇形的半径为r所以1 r2 r
, , ×4× =6⇔ =3,
2
所以该扇形的弧长l .
=43
.【答案】 3
13
5
b aa a
【解析】 根据题意 向量b a在a上的投影向量为 - 3a.
, - a ·a =
5
.【答案】 79
14
288
【解析】 根据题意 若甲队得 分 乙队得 分 若甲队得 分 乙队得 分或 分
, 2 , 1 , 3 , 1 2 ,
所以满足本题的概率为1 1 1 2 2 3 1 1 3 1 2 1 1 1
× × ×3× × × + × × + × × + × ×
2 2 2 3 3 4 3 3 4 3 3 4 2 2
1 2 1 1 1 2 3 79.
×1- × × - × × =
2 3 3 4 3 3 4 288
.【答案】 见解析
15
【解析】 fx m n x x π
(1)()= · =1+2cos ·sin +
6
x x π x 3 x 1 x
=2cos ·sin + +1=2cos sin + cos +1
6 2 2
x
x x 2x 3 x 1+cos2
=3sincos +cos +1= sin2 + +1
2 2
3 x 1 x 3 x π 3 分
= sin2 + cos2 + =sin2 + + ;……………………… (6 )
2 2 2 6 2
fA 5 A π 3 5 A π
(2)( )= ⇔sin2 + + = ⇔sin2 + =1,
2 6 2 2 6
A π π k k N 所以A π k k N
2 + = +2π(∈ ), = + π(∈ ),
6 2 6
因A在第三象限 所以A π n n N
, = +(2 +1)π(∈ ),
6
A π π n n N 分
+ = +(2 +1)π(∈ ), …………………………………………………………… (9 )
6 3
所以 A π π 1. 分
cos + =-cos =- ……………………………………………………… (13 )
6 3 2
.【答案】 见解析
16
【解析】 因为点M为BC的中点 点O是AB的中点
(1) , ,
所以OM AC
∥ ,
OM 平面SOMAC 平面SOM
⊂ , ⊄ ,
所以AC 平面SOM 分
∥ ; ……………………………………………………………………… (5 )
因为该圆锥的轴截面是 SAB
(2) △ ,
S 1 SA SB ASB ASB π或2π 分
△ SAB =43⇔ × × ×sin∠ =43⇔∠ = ……………………… (7 )
2 3 3
当 ASB π时 可得SO OB
∠ = , =23, =2,
3
高一数学参考答案 第 页(共 页)
3 5
{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}所以该圆锥的表面积为 2 1 分
π×2+ ×4×2π×2=12π,…………………………………… (10 )
2
当 ASB 2π时 可得SO OB
∠ = , =2, =23,
3
所以该圆锥的表面积为 2 1 . 分
π× 23 + ×4×2π×23=(12+83)π ……………… (15 )
2
.【答案】 见解析
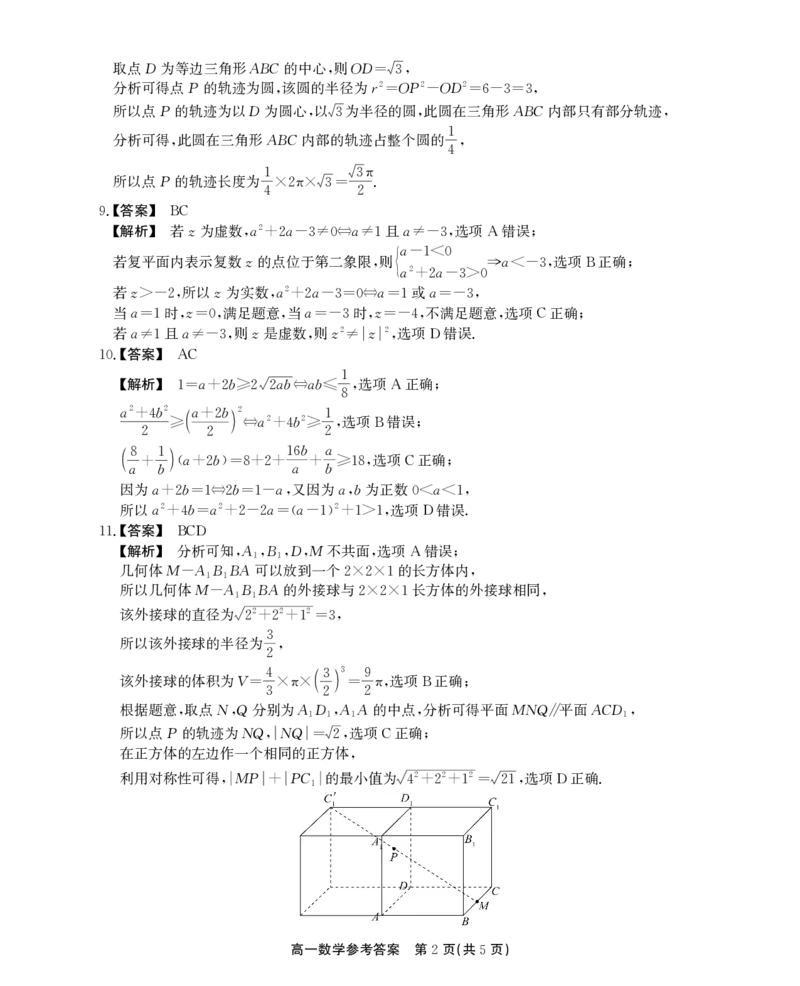
17
【解析】 根据题意 设此估计分数线为t
(1) , ,
则 . t . . t
(100-90)×001+(90- )×003=025⇔ =85,
分
………………………………………………………………………………………………… (3 )
所以此次考试成绩优胜的估计分数线为 分
85;……………………………………………… (4 )
根据分层抽样可得 抽出这 人 第二组 人 分别为a a 第四组 人 分别为b b
(2)① , 6 , 2 , 1,2, 4 , 1,2,
bb
3,4,
所以从中抽取 人 一共aa ab ab 种 满足条件的为ab ab 种
2 , 1 2,1 1,1 2,……,15 , 1 1,1 2,…,8 ,
所以概率为8 分
; ……………………………………………………………………………… (8 )
15
设第二组 第四组抽取学生的成绩的平均数与方差分别为x x s2s2
② 、 1,2;1,2,
.
且两组频率之比为015 1 分
. = ,……………………………………………………………… (10 )
030 2
则第二组和第四组所有抽取的学生成绩的平均数x 1×65+2×83 分
= =77,…………… (12 )
3
第二组和第四组所有抽取的学生成绩的方差
s2 1s2 x x2 2s2 x x2
= 1+ 1- + 2+ 2-
3 3
1 2 2 2 . 分
= 40+(65-77) + 70+(83-77) =132 …………………………………… (15 )
3 3
.【答案】 见解析
18
设 ABD的边长为 a 连接AO与OC
(1) △ 2 , ,
所以AO a 分
=3 ,……………………………………………………………………………… (1 )
又因为BC CD 所以OC 1BD a 分
⊥ , = = ,…………………………………………………… (2 )
2
又因为AC BD a 所以AO2 CO2 AC2 分
= =2 , + = ,…………………………………………… (4 )
所以AO OC 分
⊥ ;……………………………………………………………………………… (5 )
因为BC CD 所以CO BD 所以BD 平面AOC
(2) = , ⊥ , ⊥ ,
连接OE 根据题意 BEO为BE与平面AOC所成角
, ,∠ ,
OE aOB a 所以 BEO π
= , = , ∠ = ,
4
所以 BEO 2 分
cos∠ = ; ……………………………………………………………………… (9 )
2
由于BC CD在底面补成矩形BCDM 连接AMBM
(3) ⊥ , , ,
分析可得BM CD
= ,
则 ABM为异面直线AB与CD所成角或其补角 分
∠ , …………………………………… (12 )
AB2 BM2 AM2
ABM + -
cos∠ = AB BM ,
2× ×
高一数学参考答案 第 页(共 页)
4 5
{#{QQABAYYUogggAoBAAAgCAQWoCgIQkAAAAagGwBAIsAIAABNABAA=}#}点O为BD的中点 则点O为CM的中点 所以OM OC
, , = ,
又因为 AOC AOM °AO AO
∠ =∠ =90, = ,
所以 AOC AOM 所以AM AC a 分
△ ≌△ , = =2 , …………………………………………… (14 )
AB2 BM2 AM2
所以 ABM + - 1 BM CD a 分
cos∠ = AB BM = ⇔ = = ,…………………………… (16 )
2× × 4
BC
又因为BC CD 可得BC a . 分
⊥ , =3 ,CD=3 ……………………………………………… (17 )
.【答案】 见解析
19
【解析】 连接AMCN 点M N分别为边BCAB的中点
(1) , , , , ,
AM→ 1AB→ AC→ 1AB→ 1AC→
= + = + ,
2 2 2
CN→ 1CA→ CB→ 1 AC→ AB→ AC→ 1AB→ AC→ 分
= + = (- + - )= - ……………………………… (2 )
2 2 2
AM→ CN→ 1AB→ 1AC→ 1AB→ AC→
· =0⇔ + - =0
2 2 2
1AB→2 1AB→ AC→ 1AC→2 分
⇔ - · - =0, ……………………………………………………… (4 )
4 4 2
可得c2 bc A b2 分
- cos -2 =0,………………………………………………………………… (6 )
b2 c2 a2
利用余弦定理 A + -
cos = bc ,
2
b2 c2 a2
c2 bc + - b2 a2 c2 b2
- × bc -2 =0⇔ + =5 ,
2
a2 c2
所以 + 分
b2 =5;……………………………………………………………………………… (7 )
因为 ABC为锐角三角形
(2) △ ,
所以a2 b2 c2b2 c2 a2c2 a2 b2 分
+ > , + > , + > ,………………………………………………… (8 )
所以 a2 c2 c2 a2 则2
c2
3 即 6
c
6. 分
3 >2 ,3 >2 ,