文档内容
格致课堂
6.2.3 向量的数乘运算
(用时45分钟)
【选题明细表】
知识点、方法 题号
线性表示 1,2,5,7,8
向量共线 3,4,6,9
综合应用 10,11,12
基础巩固
1.下列各式计算正确的个数是( )
①(-7)·5a=-35a;②a-2b+2(a+b)=3a;③a+b-(a+b)=0.
A.0 B.1 C.2 D.3
【答案】C
【解析】根据向量数乘的运算律可验证①②正确;③错误,因为向量的和、差及数乘运算的结果仍为一个
向量,而不是实数.
2.如图所示,D是△ABC的边AB上的中点,则向量CD=( )
A.BC-BA
B.-BC+BA
C.-BC-BA
D.BC+BA
【答案】B
【解析】 ∵D是AB的中点,∴BD=BA,
∴CD=CB+BD=-BC+BA.
3.已知向量a,b,且AB=a+2b,BC=-5a+6b,CD=7a-2b,则一定共线的三点是( )
A.A,B,D B.A,B,C C.B,C,D D.A,C,D
【答案】A
【解析】 AD=AC+CD=AB+BC+CD格致课堂
=(a+2b)+(-5a+6b)+(7a-2b)
=3a+6b=3AB,
∴A,B,D三点共线.故选A.
4.若AB=3e,CD=-5e,且|AD|=|BC|,则四边形ABCD是( )
1 1
A.平行四边形 B.菱形
C.等腰梯形 D.不等腰的梯形
【答案】C
【解析】因为AB=-CD,所以AB∥CD,且|AB|≠|CD|.而|AD|=|BC|,所以四边形ABCD为等腰梯形.
5.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F.若AC
=a,BD=b,则AF等于( )
A.a+b B.a+b
C.a+b D.a+b
【答案】B
【解析】如图所示,∵E是OD的中点,∴OE=BD=b.
又∵△ABE∽△FDE,∴==.
∴AE=3EF,∴AE=AF,
在△AOE中,AE=AO+OE=a+b,
∴AF=AE=a+b.故选B.
6.设e,e 是两个不共线的向量,若向量ke+2e 与8e+ke 方向相反,则k=________.
1 2 1 2 1 2
【答案】-4
【解析】∵ke+2e 与8e+ke 共线,
1 2 1 2
∴ke+2e=λ(8e+ke)=8λe+λke.
1 2 1 2 1 2
∴解得或
∵ke+2e 与8e+ke 反向,∴λ=-,k=-4.
1 2 1 2
7.若a=-e+3e,b=4e+2e,c=-3e+12e,则向量a写为λb+λc的形式是________.
1 2 1 2 1 2 1 2
【答案】-b+c
【解析】 若a=λb+λc,则-e +3e =λ(4e +2e)+λ(-3e +12e),∴-e +3e =(4λ -3λ)e +(2λ +
1 2 1 2 1 1 2 2 1 2 1 2 1 2 1 1格致课堂
12λ)e.
2 2
∴解之,得
8.如图所示,向量OA,OB,OC的终点A,B,C在一条直线上,且AC=-3CB.设OA=p,OB=q,OC
=r,那么r用 p, q怎么表示?
【答案】r=-p+q.
【解析】∵OC=OB+BC,AC=-3CB=3BC,
∴BC=AC.
∴OC=OB+AC=OB+(OC-OA).
∴r=q+(r-p).
∴r=-p+q.
能力提升
9.已知向量a,b是两个非零向量,在下列四个条件中,一定可以使a,b共线的是( )
①2a-3b=4e且a+2b=-2e;
②存在相异实数λ,μ,使 =0;
③ =0(其中实数x,y满足x+y=0);
④已知梯形ABCD,其中
A.①② B.①③
C.② D.③④
【答案】A
【解析】由2a-3b=-2(a+2b)得到b=-4a,故①可以;λa-μb=0,λa=μb,故②可以;x=y=0,有
xa+yb=0,但b与a不一定共线,故③不可以;梯形ABCD中,没有说明哪组对边平行,故④不可以.
10.如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若
AB=mAM,AC=nAN,则m+n的值为________.格致课堂
【答案】2
【解析】在△ABC中,连接AO.由于O是BC的中点,因此AO=(AB+AC)=AB+AC.
由于AB=mAM,AC=nAN,
则AO=mAM+nAN.
由于M,O,N三点共线,则m+n=1,
从而m+n=2.
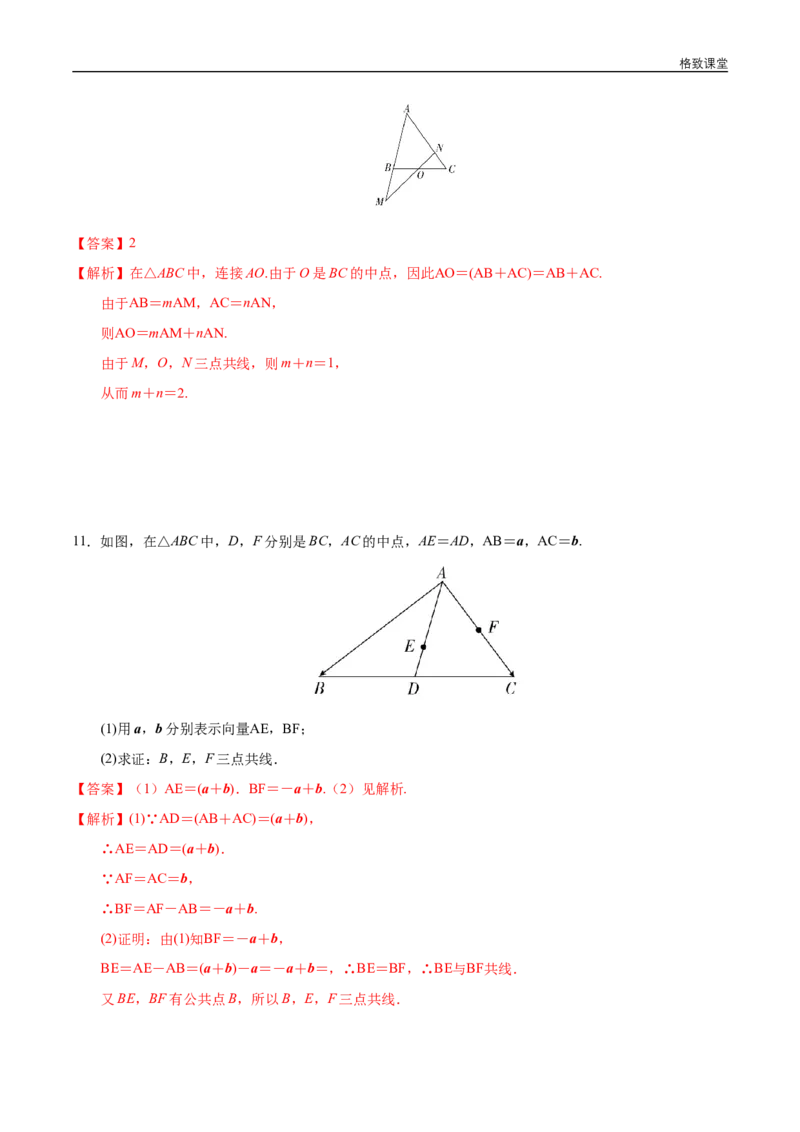
11.如图,在△ABC中,D,F分别是BC,AC的中点,AE=AD,AB=a,AC=b.
(1)用a,b分别表示向量AE,BF;
(2)求证:B,E,F三点共线.
【答案】(1)AE=(a+b).BF=-a+b.(2)见解析.
【解析】(1)∵AD=(AB+AC)=(a+b),
∴AE=AD=(a+b).
∵AF=AC=b,
∴BF=AF-AB=-a+b.
(2)证明:由(1)知BF=-a+b,
BE=AE-AB=(a+b)-a=-a+b=,∴BE=BF,∴BE与BF共线.
又BE,BF有公共点B,所以B,E,F三点共线.格致课堂
素养达成
12.设e,e 是两个不共线的向量,如果AB=3e-2e,BC=4e+e,CD=8e-9e.
1 2 1 2 1 2 1 2
(1)求证A,B,D三点共线;
(2)试确定λ的值,使2λe+e 和e+λe 共线;
1 2 1 2
(3)若e+λe 与λe+e 不共线,试求λ的取值范围.
1 2 1 2
【答案】(1)见解析.(2)λ=±.(3)当λ≠±1时,e+λe 与λe+e 不共线.
1 2 1 2
【解析】 (1)证明:因为BD=BC+CD=4e+e+8e-9e=12e-8e=4(3e-2e)=4AB,
1 2 1 2 1 2 1 2
所以AB与BD共线.
因为AB与BD有公共点B,所以A,B,D三点共线.
(2)因为2λe+e 与e+λe 共线,
1 2 1 2
所以存在实数μ,使2λe+e=μ(e+λe).
1 2 1 2
因为e,e 不共线,所以
1 2
所以λ=±.
(3)假设e+λe 与λe+e 共线,则存在实数μ,使e+λe=μ(λe+e).
1 2 1 2 1 2 1 2
因为e,e 不共线,所以所以λ=±1.
1 2
所以当λ≠±1时,e+λe 与λe+e 不共线.
1 2 1 2