文档内容
2024~2025 学年度第二学期期中学业水平诊断
高一数学
注意事项:
1.本试题满分150分,考试时间为120分钟.
2.答卷前,务必将姓名和准考证号填涂在答题纸上.
3.使用答题纸时,必须使用0.5毫米的黑色签字笔书写,要字迹工整,笔迹清晰;超出答题区
书写的答案无效;在草稿纸、试题卷上答题无效.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符
合题目要求.
1. 已知复数z满足 ,则z的虚部为( )
A. B. C. D.
【答案】B
【详解】设 ,
由 ,得 ,
所以 ,即 ,解得
所以 ,所以复数 的虚部为 .
故选:B.
2. 若 ,则 ( )
A. B. C. D.
【答案】B【详解】由 ,
因为 ,所以上式 ,
故选:B.
3. 在平面直角坐标系中,已知 ,则向量 在 上的投影向量为( )
A. B.
C. D.
【答案】C
【详解】由已知得:
根据 在 投影向量公式可得:
,
故选:C.
4. 在 中, ,M是AN上一点,且 ,则实数 的值为( )
A. B. C. D.
【答案】D
【详解】因为 三点共线,设 ,
又因为 ,可得
,
因为 ,可得 ,可得 .
故选:D.
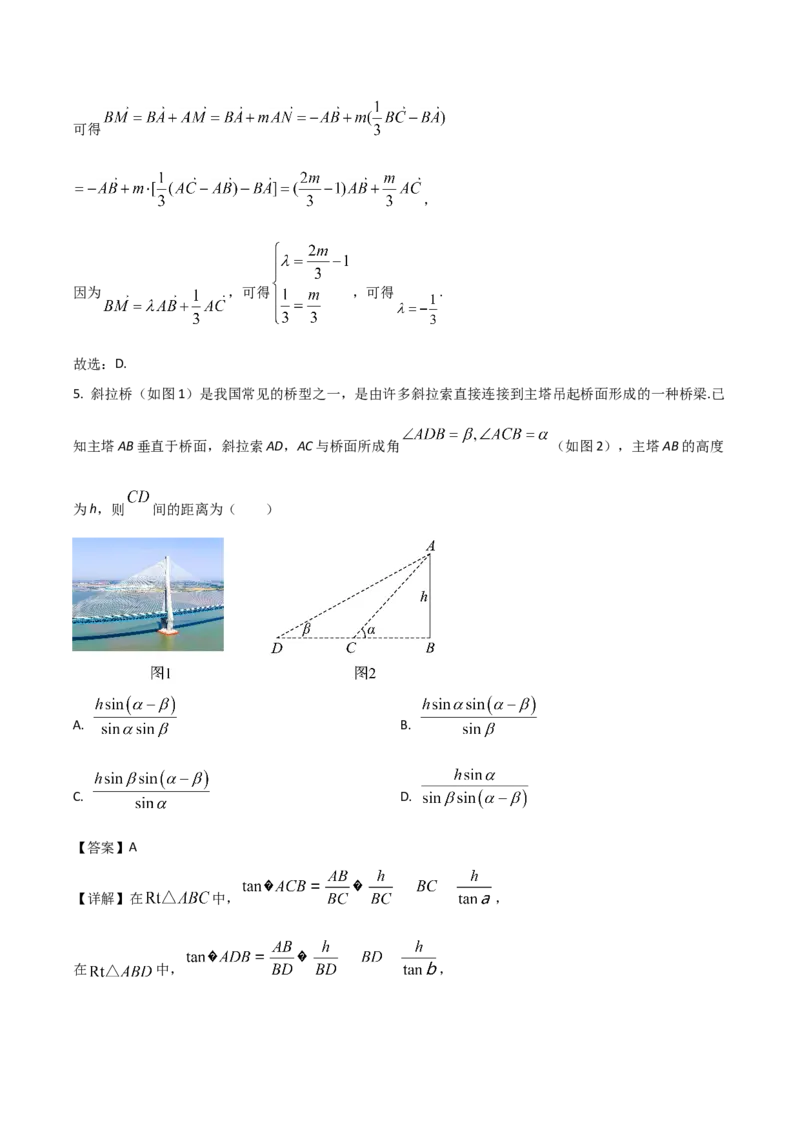
5. 斜拉桥(如图1)是我国常见的桥型之一,是由许多斜拉索直接连接到主塔吊起桥面形成的一种桥梁.已
知主塔AB垂直于桥面,斜拉索AD,AC与桥面所成角 (如图2),主塔AB的高度
为h,则 间的距离为( )
A. B.
C. D.
【答案】A
【详解】在 中, ,
在 中, ,所以
,
故选:A.
6. 若函数 在 上的最小值为 ,则t的最大值为( )
A. B. C. D.
【答案】D
【详解】由 ,可得 ,
因为 ,
要使得 上 最的小值为 ,则满足 ,
解得 ,所以 ,所以 的最大值为 .
故选:D.
7. 若 ,则 ( )
A. B. C. D.
【答案】C
【详解】由题得 ,所以 ,
整理得 ,解得 或 (舍),
所以 ,
故选:C.
8. 的内角 的对边分别为 ,已知 ,且 ,
边上的中线 相交于点P,且 ,则四边形 的面积为( )
A. 1 B. C. 2 D.
【答案】D
【详解】由 ,结合正弦定理边化角得: ,
因为 ,所以上式化为 ,再由内角和为 可化为 ,
利用三角恒等变形得: ,因为 ,所以 ,
即上式变形为 ,又因为 ,所以 ,再由余弦定理得:
即 ,解得 ,
可得 或 ,因为 ,所以 ,
则 的面积为 ,
因为 边上的中线 相交于点P,所以点P是 的重心,
即 , ,
由 ,所以 ,
即四边形 的面积为 ,
故选:D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合要求.
全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的有( )
A. 若向量 满足 且 ,则
B. 对于任意向量 ,都有C. 对于任意向量 ,都有
D. 若向量 共线,则存在实数 ,使得
【答案】BC
【详解】对于A,若 ,则 ,
若 ,则 ,显然 ,故A错误;
对于B, ,因为 ,所以 ,
所以 ,故B正确;
对于C,根据向量三角不等式, ,故C正确;
对于D,若 ,则不存在实数 ,使得 ,故D错误;
故选:BC.
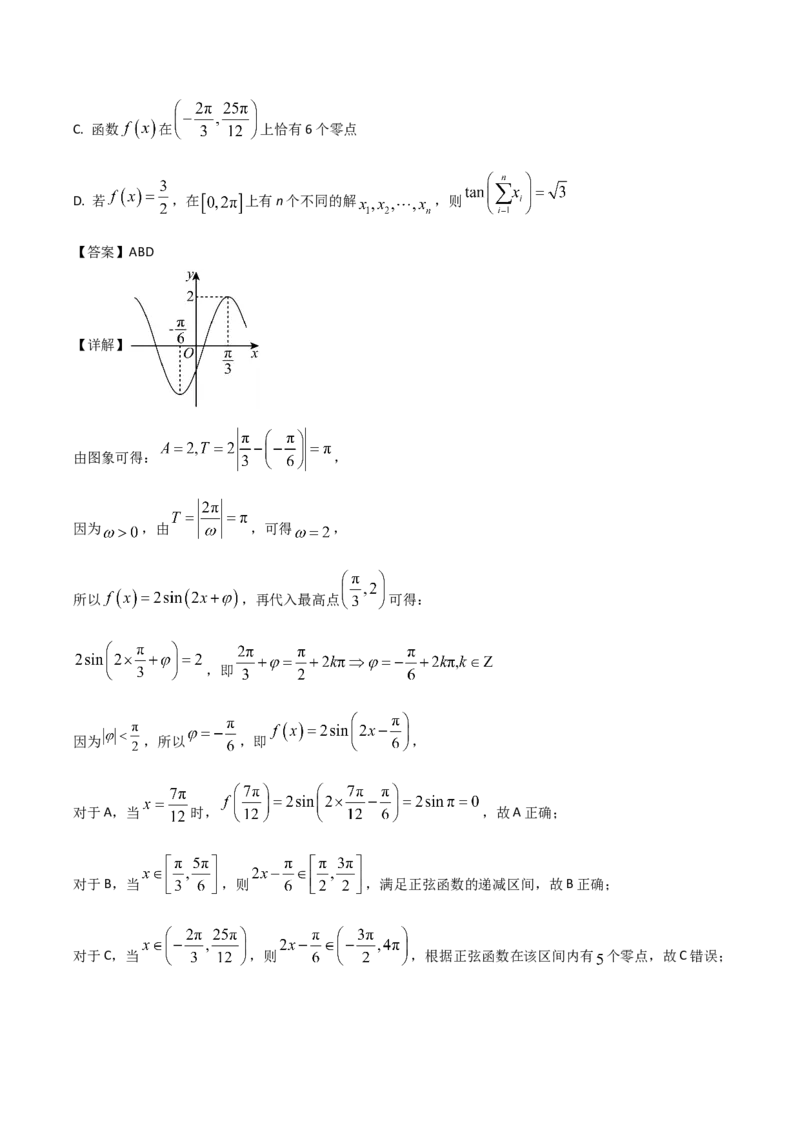
10. 函数 的部分图象如图所示,则( )
A. 函数 的图象关于点 对称
B. 函数 在 上单调递减C. 函数 在 上恰有6个零点
D. 若 ,在 上有n个不同的解 ,则
【答案】ABD
【详解】
由图象可得: ,
因为 ,由 ,可得 ,
所以 ,再代入最高点 可得:
,即
因为 ,所以 ,即 ,
对于A,当 时, ,故A正确;
对于B,当 ,则 ,满足正弦函数的递减区间,故B正确;
对于C,当 ,则 ,根据正弦函数在该区间内有 个零点,故C错误;对于D,当 ,作图分析可知;
方程 在 上存在四个解,可知它们分别关于直线 对称,
即有 所以有
即 故D正确;
故选:ABD.
11. 已知 的面积为S,角A,B,C的对边分别为a,b,c,且 ,则下列说法正确的有(
)
A. B. 若 ,则
C. 若 ,则 D. 的最小值为
【答案】ACD
【详解】对于A中,由余弦定理得 ,
因为 ,可得 和 ,可得 ,
又由正弦定理,可得 ,即 ,所以 ,所以A正确;
对于B中,由 ,
可得 ,解得 ,
因为 ,所以 或 ,所以B不正确;
对于C中,由 ,且 ,可得 ,所以 ,
因为 ,由正弦定理 ,可得 ,
又由 ,
所以 的面积为 ,所以C正确;
对于D中,由 ,可得
可得 ,
则 ,
当且仅当 时,即 时,即 ,等号成立,所以D正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知向量 ,且 ,则 _________.【答案】
【详解】因为 ,所以 ,解得 ,
所以 ,则 ,
故答案为: .
13. 已知 ,则 _________.
【答案】
【详解】由 ,可得 ,
因 为 ,可得 ,
又由
.
故答案为: .
14. 如图,在四边形ABCD中, , ,设 .
①当 时,BF的长为______,②四边形BFDE面积的最大值为__________.【答案】 ①. ②.
【详解】解:由 ,且 ,
所以 为 的中点,且 为 的平分线,
因为 ,可得 ,
所以 ,
则 ,
所以 .
由 ,可得 ,且 ,
所以 , ,
因为 为 的中点,可得 ,
所以 ,
因为 ,可得 ,则 ,当 时,即 时,可得 的最大值为 .
四、解答题.本题共5小题,共7分.解答应写出文字说明、证明过程或演算步骤.
15. 已知复数 .
(1)若 为纯虚数,求复数 的值;
(2)若 为虚数且在复平面内对应的点在直线 上,求 的值.
【答案】(1) ;
(2) .
【小问1详解】
由 为纯虚数,
可得 ,解得 ,此时 ,
则 .
【小问2详解】
由 为虚数且在复平面内对应的点在直线 上,
则 ,解得 或 ,
由于 为虚数,所以 舍去,故 则 ,
则 .
的
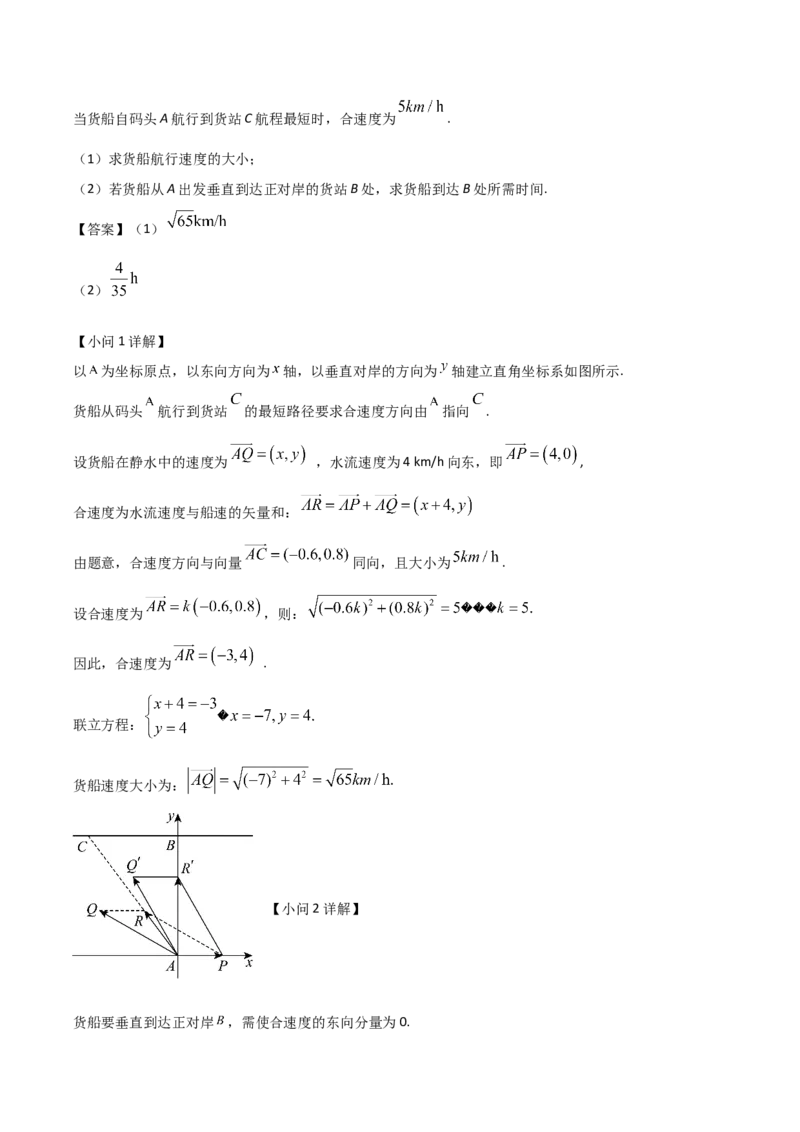
16. 一条东西方向 河流两岸平行,河宽800m,水流的速度为向东 .河南岸有一码头A,码头A正
对面有一货站B(AB与河的方向垂直),B的正西方向且与B相距600m另有货站C,已知一货船匀速航行,当货船自码头A航行到货站C航程最短时,合速度为 .
(1)求货船航行速度的大小;
(2)若货船从A出发垂直到达正对岸的货站B处,求货船到达B处所需时间.
【答案】(1)
(2)
【小问1详解】
以 为坐标原点,以东向方向为 轴,以垂直对岸的方向为 轴建立直角坐标系如图所示.
货船从码头 航行到货站 的最短路径要求合速度方向由 指向 .
设货船在静水中的速度为 ,水流速度为4 km/h向东,即 ,
合速度为水流速度与船速的矢量和:
由题意,合速度方向与向量 同向,且大小为 .
设合速度为 ,则:
因此,合速度为 .
联立方程:
货船速度大小为:
【小问2详解】
货船要垂直到达正对岸 ,需使合速度的东向分量为0.设船速为 ,则:
由(1)知船速大小为 ,故:
合速度的北向分量为 ,河宽 ,所需时间为:
17. 已知函数 图象的相邻两条对称轴间的距离为 .
(1)求 的值及函数 的单调递增区间;
(2)将函数 的图象向右平移 个单位长度,再把各点的横坐标缩小为原来的 (纵坐标不变),
得到函数 的图象,若对任意的 ,不等式 恒成立,求实数 的取值范
围.
【答案】(1) ;
(2)
【小问1详解】
由 ,
由其图象的相邻两条对称轴间的距离为 ,可知最小正周期为 ,
因为 ,所以 ,即 ,
由 , ,解得 , ,所以函数 的单调递增区间为 , .
【小问2详解】
将函数 的图象向右平移 个单位长度可得, ,
再把各点的横坐标缩小为原来的 (纵坐标不变),得到函数 的图象,
即 ,
对任意的 ,有 ,此时 ,
此时有 ,
要使得不等式 恒成立,则只需要满足 ,解得 或 ,
故实数 的取值范围这 .
18. 在 中,内角 所对的边分别为a,b,c.从下面两个条件中任选一个作答,如果选择多个
条件分别解答,按第一个解答计分.① ;② .
(1)求角B;
(2)若 ,求 的取值范围.
【答案】(1) ;
(2)
【小问1详解】选①:
由 ,利用正弦定理边化角得: ,
因为 ,所以有 ,
可得 ,
因为 ,所以 ;
选②:
由 ,利用正弦定理边化角得: ,
因为 ,所以有 ,
可得: 因 为,所以 ,且 ;
【小问2详解】
若 ,求 的取值范围.
用正弦定理边化角可得:
,
因为 ,所以 ,即 ,则 ,所以 ,即 ,
则 .
19. 在 中, .
(1)求 ;
(2)若 的面积为18, 的平分线与边BC交于点D,求AD的长.
【答案】(1)
(2)
【小问1详解】
解:在 中,可得 ,
所以 ,
且 ,
因为 ,可得 ,
所以 ,
又因为 ,所以 ,
因为 ,可得 ,解得 ,
又因为 ,可得 ,所以 .【小问2详解】
解:由 的面积为18,可得 ,所以 ,
因为 ,且 ,可得 为锐角,所以 ,
又由 ,
所以 ,
由正弦定理,可得 ,即 ,
联立方程组 ,可得 ,
因为 ,可得 ,
又因为 的平分线与边BC交于点D,设 ,
因为 ,所以 ,
即 .