文档内容
山东省青岛第五十八中学2025-2026学年高一上学期期中考试
数学试题
一、单选题
1.设集合 , ,则 ( )
A. B. C. D.
2.“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若幂函数 的图象经过点 ,则 ( )
A. B. C. D.4
4.若 ,则 的大小关系是( )
A. B. C. D.
5.函数 的大致图象是( )
A. B.
C. D.6.关于 的不等式 的解集中恰有2个整数,则实数 的取值范围是( )
A. B.
C. D.
7.已知 , , ,若 恒成立,则实数 的取值范围为( )
A. B. C. D.
8.已知 ,对任意的 , 恒成立,则实数 的最小值是( ).
A. B. C. D.
二、多选题
9.下列各式化简正确的是( )
A. B.
C. D.
10.若一个函数的定义域与值域相同,则称这个函数为同域函数,则下列函数为同域函数的是( )
A. B.
C. D.
11.已知 是定义在 上的函数;对于任意实数 满足 ,当 时, ,
则( )
A.
B.C.方程 有3个实数根
D.若 ,则 或
三、填空题
12.若函数 的定义域为 ,则函数 的定义域是 .
13.若不等式 的解集为 ,则 的值为
14. ,若 在定义域内单调递增,则实数a的取值范围是 .
四、解答题
15.求值:
(1) ;
(2) .
16.已知集合 , .
(1)若 ,求 , ;
(2)若 ,求实数 的取值范围.
17.中山市翠亨新区现有一人工智能企业,生产制造人形机器人.每月的成本t(单位:万元)由两部分构成:
①固定成本:1000万元;②材料成本: 万元,x为每月生产人形机器人的个数.
(1)该企业每月的产量为多少时,平均每个人形机器人的成本最低,最低为多少万元?(2)若每个人形机器人的售价为 万元,假设生产出来的每个人形机器人都能够售出,则该企业应如
何制订生产计划,才能确保每月的利润不低于400万元?附:利润 售价 销量 成本.
18.已知函数 .
(1)求 的定义域,并求 , 的值;
(2)观察(1)中的函数值,请猜想 具有的两个性质,并选择其中一个加以证明;
(3)解不等式: .
19.对于定义域为 的函数 ,如果存在区间 ,使得函数 在x∈ 时,值域是
,则称 为 的“k倍美好区间”.特别地,若函数函数 在x∈ 时值域是 ,
则称 为 的“完美区间”.
(1)证明:函数 在定义域里存在“完美区间”;
(2)如果二次函数 在(0,+∞)内存在“2倍美好区间”,求出a,b;
(3)是否存在实数 ,使得函数 ( )在区间 单调,且 为 的
“k倍美好区间”,若存在,求出k的取值范围;若不存在,请说明理由.
20.在 中, ,求 的取值范围.参考答案
1.D
【详解】 , ,
则 .
故选:D
2.A
【详解】因为 ,所以 或 ,
则 可以推出 ,但 不能推出 .
故“ ”是“ ”的充分不必要条件,
故选:A.
3.D
【详解】设幂函数 ,由于图象经过点 ,所以 ,即 ,
所以 ,则 .
故选:D.
4.C
【详解】由 在 上单调递减可知, ,即
由 在 上单调递增可知, ,即 ,
综上所述, .
故选:C.
5.D
【详解】由函数 ,
当 时,根据函数 与函数 在 上单调递增,则函数 在 的单调递增,故排除BC;
当 时, ,故排除A,则D正确.
故选:D.
6.A
【详解】由 可得 ;
若 ,则不等式解集为空集;
若 ,则不等式的解集为 ,此时要使不等式解集中恰有2个整数,
则这两个整数为2、3,则 ;
若 ,则不等式的解集为 ,此时要使不等式解集中恰有2个整数,
则这两个整数为 ;所以 ;
综上 或 ,
故选:A
7.A
【详解】因为 恒成立,所以 .
又因为 , , ,
所以 ,
当且仅当 ,即 时等号成立,
所以 ,即 ,所以 .
故选:A.
8.C
【详解】由题意,函数 ,可得 为奇函数,且在 上单调递增,由 恒成立,即 恒成立,
又由 ,
所以 ,即 ,
把不等式的恒成立转化为“对任意的 , 恒成立”.
当 时显然不成立,
当 时,则满足 ,解得 .
故选C.
9.AC
【详解】对于A, ,A正确,
对于B, ,B错误,
对于C,因为 , , , ,
所以 ,C正确,
对于D,因为 ,
,
所以 ,D错误,
故选:AC.
10.ABD
【详解】对于A,因为 的定义域与值域均为 ,所以 是同域函数,A选项正确;
对于B,因为 的定义域与值域均为 ,所以 是同域函数,B选项正确;对于C,对于函数 ,其定义域为 ,当 时, ,所以 不是同域函数,C选
项错误;
对于D,因为 ,由 得 ,
所以 的定义域与值域均为 ,所以 是同域函数,D选项正确.
故选:ABD.
11.ACD
【详解】对于A:令 ,则 ,所以 ,故A正确;
对于B:令 , ,
所以 ,令 ,所以 ,
所以 ,所以 为奇函数,故B错误;
对于C:令 ,所以 ,所以 ,
当 时,所以 ,则 ,
当 时, ,所以 , ,又 ,
所以 为奇函数,且定义域为 ,所以 ,又 ,
所以方程 有3个实数根,故C正确;
对于D:由 , ,
又 ,若 ,则 ,
当 时,所以 ,则 ,满足题意,当 时, ,所以 , ,不满足题意,
当 时, , ,
又 为奇函数,所以 ,满足题意,
当 时, ,
由 为奇函数,所以 ,不满足题意,
所以,若 ,则 或 ,故D正确,
故选:ACD.
12.
【详解】因为函数 的定义域为 ,
则对于函数 ,令 ,解得 ,
所以函数 的定义域是 .
故答案为:
13.
【详解】因为不等式 的解集为: ,得: ,
即方程 的两个根为 和 ,
由根与系数的关系得 , ,
解得: , ,所以: .
故答案为: .14.
【详解】解:由于函数 在 和 上递减,在 的 上递增,
∵ 在定义域内单调递增;
∴ ,解得 ;
∴实数a的取值范围为: .
15.(1)
(2)
【详解】(1)
;
(2)
.
16.(1) ,
(2) 或 .
【详解】(1)当 时, ,
,
或 ,.
(2) , ,
则当 时, ,解得 ,满足题意;
当 时, ,解得 ,
综上,实数 的取值范围为 或 .
17.(1)每月的产量为100个时,平均每个人形机器人的成本最低,最低为30万元
(2)每月生产不小于70个人形机器人,才能确保每月的利润不低于400万元
【详解】(1)设平均每个人形机器人的成本为 万元,根据题意有
,
当且仅当 ,即 时取等号,
所以该企业每月的产量为100个时,平均每个人形机器人的成本最低,最低为30万元.
(2)设月利润为 万元,则有 ,
由题知 ,整理得 ,解得 (舍去)或 ,
所以该企业每月生产不少于70个人形机器人,才能确保每月的利润不低于400万元.
18.(1)
(2)答案见解析
(3)
【详解】(1)由 ,得 ,即函数 定义域为 ,
则 ,;
(2)猜想性质1: 为奇函数;
证明:函数 定义域为 ,
则 ,故 为奇函数;
猜想性质2:函数 在定义域 上单调递减,
证明:取 ,
则
,
因为 ,故 ,
则 ,故 ,
即 ,
故 在定义域 上单调递减.
(3)由(2)知 为奇函数,故 即 ,
又 在定义域 上单调递减.,
故 ,解 ,即 ,
解 ,即 ,
解
得 ,故 的解集为 .
19.(1)证明见解析
(2) , .
(3)存在,
【详解】(1) 在 与 上均为增函数,若 存在完美区间 ,则有
,即 为 的两根.
即 的根,故 ,即存在“完美区间”.
(2)若 存在“2倍美好区间”,则设定义域为 ,值域为
当 时,易得 在区间上单调递减,
则 ,两式相减可得 ,得 ,
则 ,即 ,因为 ,解得 , .
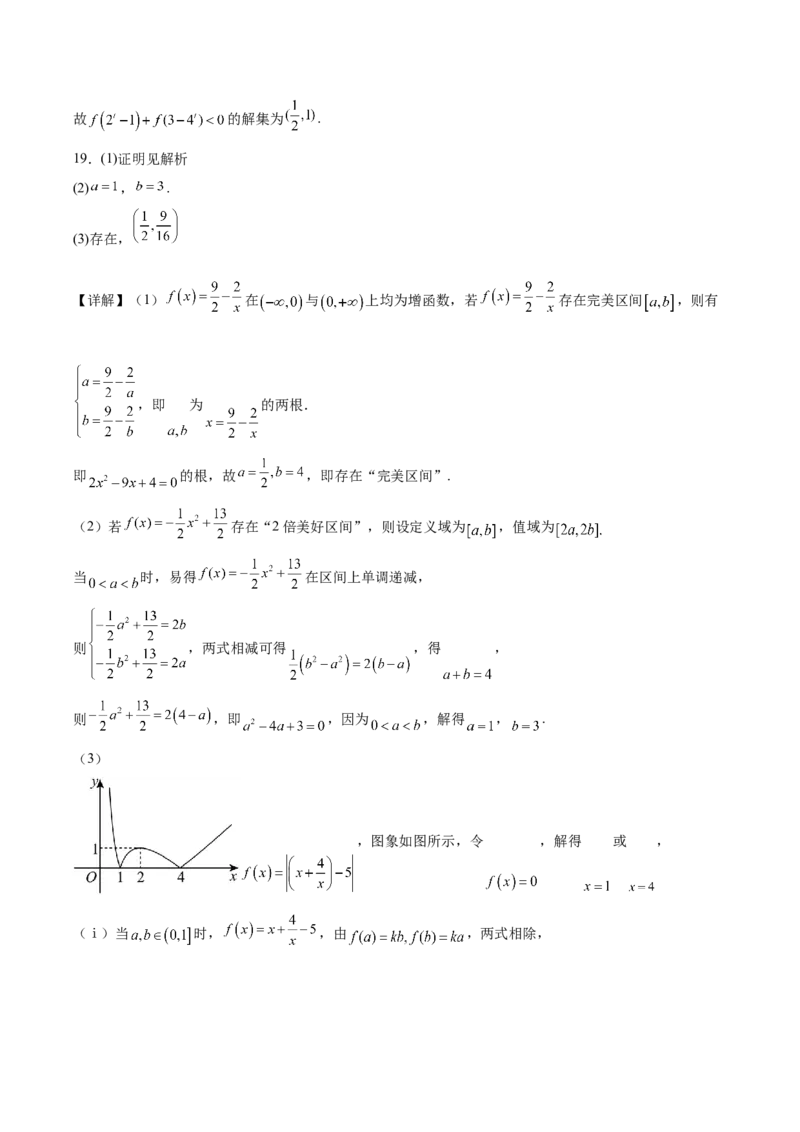
(3)
,图象如图所示,令 ,解得 或 ,
(ⅰ)当 时, ,由 ,两式相除,,
,
,可得 ,与a,b范围矛盾,即实数 不存在
(ⅱ)当 时, ,由 可得, ,即
,
,由 ,即 ,解得 ,
又 , , ,
由 ,可得 ,
综上,符合条件的k的取值范围为 .
20.
【详解】因为 , ,
所以 ,所以 , , ,
因为 ,所以 ,且 ,且 ,
所以因为 ,且 ,且 ,
所以 ,且 ,且
所以 ,且 ,
令 ,
所以 ,
令 ,易知 在 上是增函数,
所以 在 上单调递增,
所以 ,
故 ,