文档内容
2023-2024学年广西南宁市高一(下)期末数学试卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1.(5分)若复数z=1+i﹣2i3,则|z|=( )
A. B. C. D.
2.(5分)已知全集U={﹣2,﹣1,0,1,3,5},0,1,3},B={﹣2,0,则( A)∩B=( )
U
A.{﹣1,5} B.{﹣2,5} C.{﹣2,0,5} D.{﹣2,﹣∁1,5}
3.(5分)“a>3”是“a2﹣3a>0”成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.(5分)已知平面 ∥平面 ,a,b是平面 , 外两条不同的直线( )
A.若a∥ ,则a∥α β αB.β 若b⊥ ,则b⊥
C.若a∥α,b∥ ,β则a∥b D.若a⊥α,b⊥ ,β则a∥b
5.(5分)已α知球Oβ的半径R=5,球O的内接圆锥的高hα与底面β半径r的比为3:1,则该圆锥的体积为
( )
A.15 B.18 C.27 D.32
6.(5分π)高二(1)班有40名π学生,其中男生有16π名,总平均体重为60.π1kg,则女生的平均体重约为
( )
A.55.8kg B.54.6kg C.52.4kg D.51.8kg
7.(5分)已知函数 (a>1且a≠2)在R上单调递增,则实数a的取值
范围是( )
A.(1,2)∪(2,+∞) B.(2,+∞)
C.[3,+∞) D.[4,+∞)
8.(5 分)已知函数 ,若对任意的实数 t,f(x)在区间
第1页(共20页)
学科网(北京)股份有限公司,3],则 的取值范围为( )
A.(0,2) B.ω(0,3) C.(2,+∞) D.(3,+∞)
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全
部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)已知实数a,b,c满足a>b>c,a+b+c=0,则( )
A.a2>ab B.b2>bc C.bc<c2 D.a2>c2
(多选)10.(6分)在△ABC中,内角A,B,C的对边分别是a,b,c,则( )
A.若 ,则
B.若a=1,c=2,则
C.若 ,则
D.若 ,则
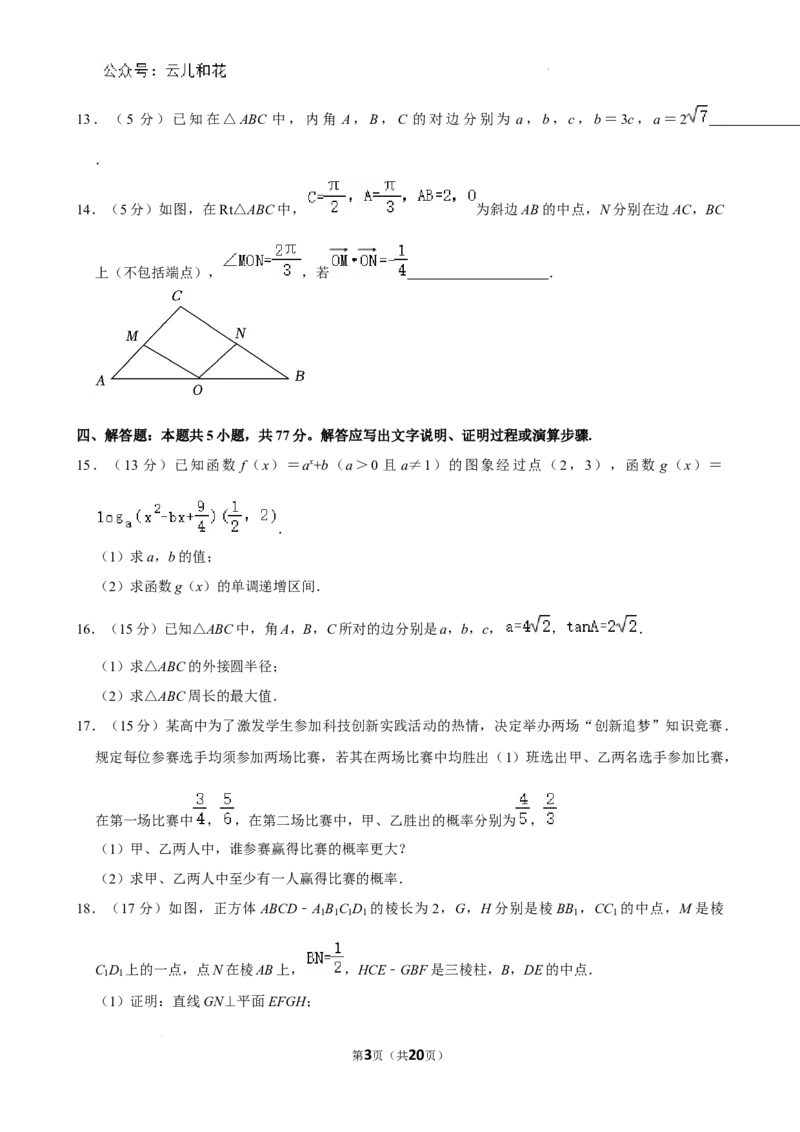
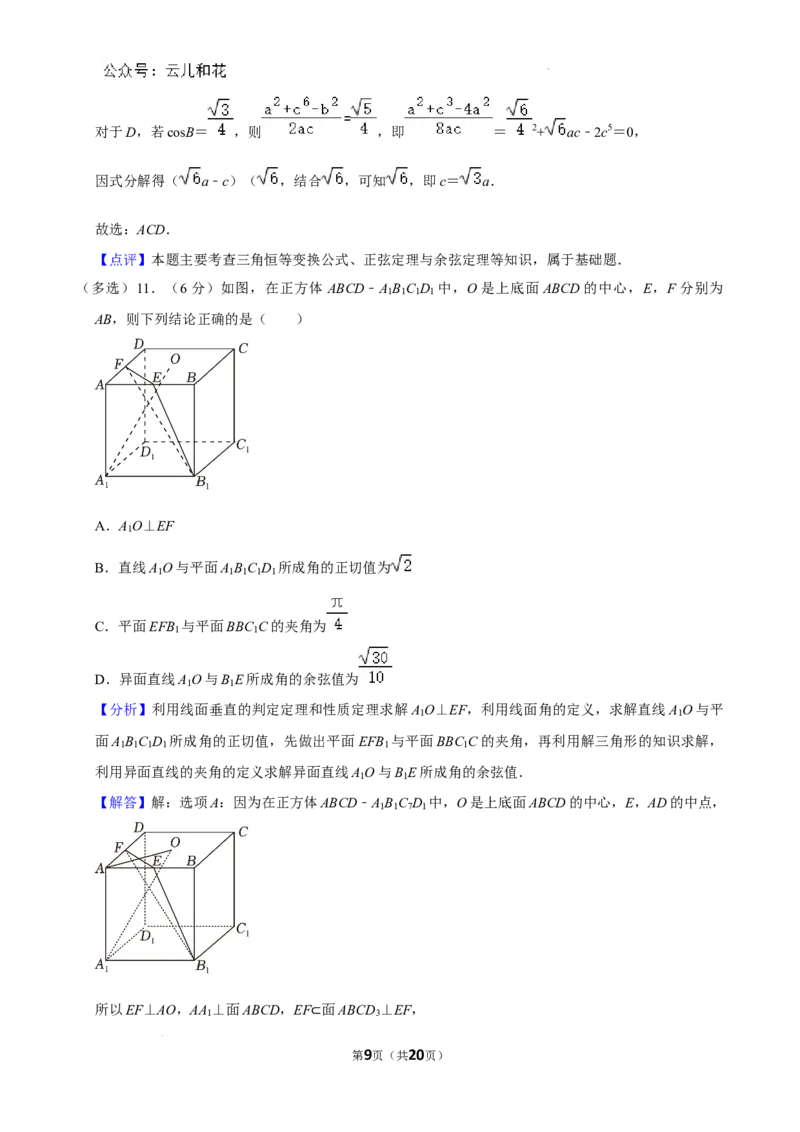
(多选)11.(6分)如图,在正方体 ABCD﹣A B C D 中,O是上底面ABCD的中心,E,F分别为
1 1 1 1
AB,则下列结论正确的是( )
A.A O⊥EF
1
B.直线A O与平面A B C D 所成角的正切值为
1 1 1 1 1
C.平面EFB 与平面BBC C的夹角为
1 1
D.异面直线A O与B E所成角的余弦值为
1 1
三、填空题:本题共3小题,每小题5分,共15分.
12.(5分)样本数据7,11,12,15,19 .
第2页(共20页)
学科网(北京)股份有限公司13.(5 分)已知在△ABC 中,内角 A,B,C 的对边分别为 a,b,c,b=3c,a=2
.
14.(5分)如图,在Rt△ABC中, 为斜边AB的中点,N分别在边AC,BC
上(不包括端点), ,若 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤.
15.(13 分)已知函数 f(x)=ax+b(a>0 且 a≠1)的图象经过点(2,3),函数 g(x)=
.
(1)求a,b的值;
(2)求函数g(x)的单调递增区间.
16.(15分)已知△ABC中,角A,B,C所对的边分别是a,b,c, , .
(1)求△ABC的外接圆半径;
(2)求△ABC周长的最大值.
17.(15分)某高中为了激发学生参加科技创新实践活动的热情,决定举办两场“创新追梦”知识竞赛.
规定每位参赛选手均须参加两场比赛,若其在两场比赛中均胜出(1)班选出甲、乙两名选手参加比赛,
在第一场比赛中 , ,在第二场比赛中,甲、乙胜出的概率分别为 ,
(1)甲、乙两人中,谁参赛赢得比赛的概率更大?
(2)求甲、乙两人中至少有一人赢得比赛的概率.
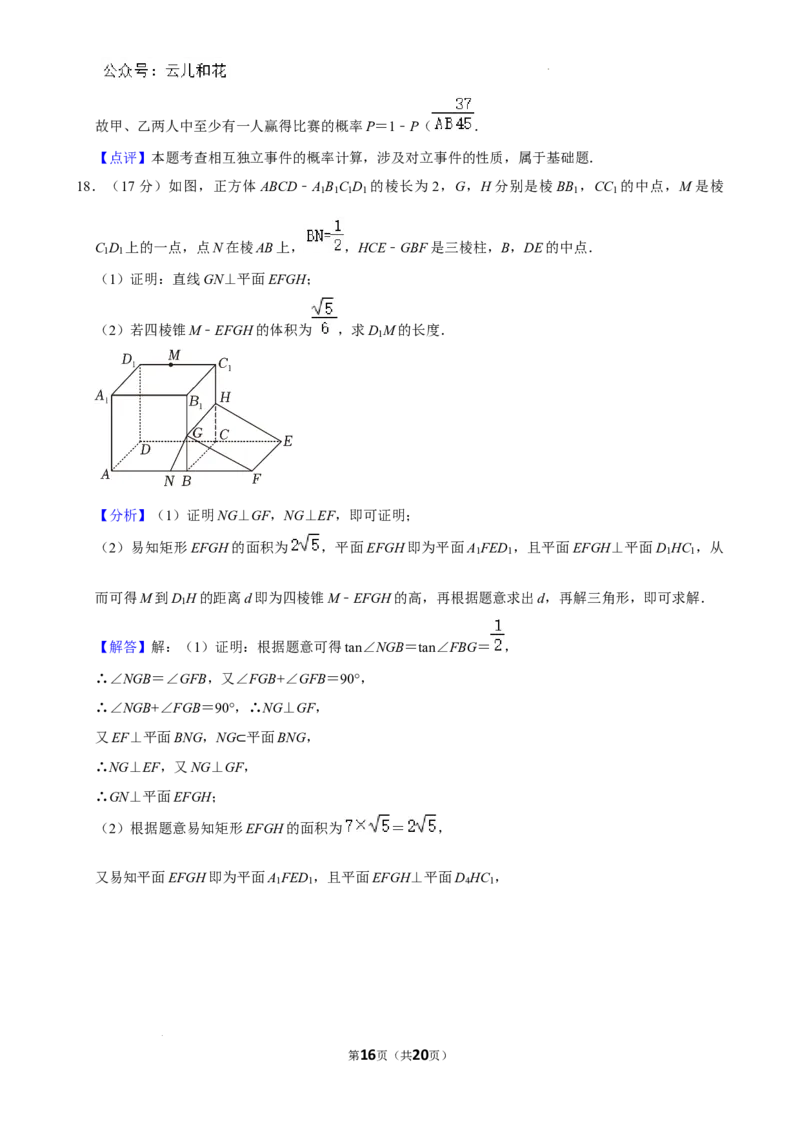
18.(17分)如图,正方体ABCD﹣A B C D 的棱长为2,G,H分别是棱BB ,CC 的中点,M是棱
1 1 1 1 1 1
C D 上的一点,点N在棱AB上, ,HCE﹣GBF是三棱柱,B,DE的中点.
1 1
(1)证明:直线GN⊥平面EFGH;
第3页(共20页)
学科网(北京)股份有限公司(2)若四棱锥M﹣EFGH的体积为 ,求D M的长度.
1
19 . ( 17 分 ) 对 于 平 面 向 量 , 记
, 若 存 在 , 使 得
是 的“k向量”.
m
Ω
(1)设 ,若 是 的“﹣3向量”,求实数l的取值范围;
3
Ω
(2)若 ,则 是否存在“1向量”?若存在,
求出“1向量”,请说明理由;
( 3 ) 已 知 均 为 的 “ ﹣ 1 向 量 ” , 其 中
3
Ω
. 设 平 面 直 角 坐 标 系 xOy 中 的 点 列
( 与原点O重合),且P 与 关
2k
于点P 对称,P 与P 关于点P 对称.求 的取值范围.
1 2k+1 2k+2 2
第4页(共20页)
学科网(北京)股份有限公司2023-2024学年广西南宁市高一(下)期末数学试卷
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1.(5分)若复数z=1+i﹣2i3,则|z|=( )
A. B. C. D.
【分析】由复数的模的运算性质进行计算即可.
【解答】解:z=1+i﹣2i=5+i+2=3+i,
所以|z|= .
故选:C.
【点评】本题考查了复数的模的运算,属于基础题.
2.(5分)已知全集U={﹣2,﹣1,0,1,3,5},0,1,3},B={﹣2,0,则( A)∩B=( )
U
A.{﹣1,5} B.{﹣2,5} C.{﹣2,0,5} D.{﹣2,﹣∁1,5}
【分析】根据题意,先求出 A,由交集定义计算可得答案.
U
【解答】解:根据题意,全∁集U={﹣2,0,5,3,5},6,1,3}
U
A={﹣2,5},
又由B={﹣2,8,5},
则( A)∩B={﹣2,2}.
U
故选∁:B.
【点评】本题考查集合交集、补集的混合运算,注意集合交集、补集的定义,属于基础题.
3.(5分)“a>3”是“a2﹣3a>0”成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【分析】根据题意,由比较法分析充分性成立,解不等式可得必要性不成立,结合充分必要条件的定
义分析可得答案.
【解答】解:根据题意,若a>32﹣2a=a(a﹣3)>0,
反之,若a5﹣3a>0,即a(a﹣2)>0,则a>3不一定成立.
故“a>2”是“a2﹣3a>6”成立的充分不必要条件.
第5页(共20页)
学科网(北京)股份有限公司故选:A.
【点评】本题考查充分必要条件的判断,涉及不等式的解法,属于基础题.
4.(5分)已知平面 ∥平面 ,a,b是平面 , 外两条不同的直线( )
A.若a∥ ,则a∥α β αB.β 若b⊥ ,则b⊥
C.若a∥α,b∥ ,β则a∥b D.若a⊥α,b⊥ ,β则a∥b
【分析】根α据空间β中各要素的位置关系,针对各个选项分α 别判定β 即可.
【解答】解:∵平面 ∥平面 ,a,b是平面 ,
∴对A选项,若a∥ α,∴A选β项正确; α
对B选项,若b⊥ ,α∴B选项正确;
对C选项,若a∥α,则a与b相交或异面或平行;
对D选项,若a⊥α,则a∥b.
故选:C. α
【点评】本题考查空间中各要素的位置关系的判定,属基础题.
5.(5分)已知球O的半径R=5,球O的内接圆锥的高h与底面半径r的比为3:1,则该圆锥的体积为
( )
A.15 B.18 C.27 D.32
【分析π】根据题意建立方程,π可求出r,h,再根据圆π锥的体积公式,即可π求解.
【解答】解:根据题意可得 ,
解得r=3,∴h=9,
∴该圆锥的体积为 = =27 .
故选:C. π
【点评】本题考查圆锥的体积的求解,属基础题.
6.(5分)高二(1)班有40名学生,其中男生有16名,总平均体重为60.1kg,则女生的平均体重约为
( )
A.55.8kg B.54.6kg C.52.4kg D.51.8kg
【分析】根据题意,设女生的平均体重为x,分析可得68.4×16+24x=60×60.1,解可得答案.
【解答】解:根据题意,设女生的平均体重为x,
高二(1)班有40名学生,其中男生有16名,
已知男生平均体重为68.4kg,总平均体重为60.1kg,
第6页(共20页)
学科网(北京)股份有限公司解可得:x≈54.3,即女生的平均体重约为54.6kg.
故选:B.
【点评】本题考查平均数的计算,注意总体平均数的计算,属于基础题.
7.(5分)已知函数 (a>1且a≠2)在R上单调递增,则实数a的取值
范围是( )
A.(1,2)∪(2,+∞) B.(2,+∞)
C.[3,+∞) D.[4,+∞)
【分析】利用分段函数的单调性,列出不等式组,求解即可.
【解答】解:函数 (a>5且a≠2)在R上单调递增,
可得 ,
解得a≥3,即a [3.
故选:C. ∈
【点评】本题考查分段函数的单调性的应用,是中档题.
8.(5 分)已知函数 ,若对任意的实数 t,f(x)在区间
,3],则 的取值范围为( )
A.(0,2) B.ω(0,3) C.(2,+∞) D.(3,+∞)
【分析】根据三角恒等变换化简函数解析式,再根据余弦型函数的值域与周期性可得解.
【解答】解:由 ,
函数值域为[﹣1,3],f(x)在区间 ,3],
则 ,
解得 >8.
故选:ωD.
【点评】本题考查三角函数的周期性的应用,主要考查学生的运算能力,属于中档题.
第7页(共20页)
学科网(北京)股份有限公司二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全
部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)已知实数a,b,c满足a>b>c,a+b+c=0,则( )
A.a2>ab B.b2>bc C.bc<c2 D.a2>c2
【分析】根据题意,由作差法分析A、C,举出反例说明B、D错误,综合可得答案.
【解答】解:根据题意,实数a,b,a+b+c=0,
依次分析选项:
对于A,a2﹣ab=a(a﹣b)>6,则a2>ab,A正确;
对于B,当b=0时,b2>bc,B错误;
对于C,c<0,则有bc﹣c2=c(b﹣c)<8,则bc<c2,C正确;
对于D,当a=2,c=﹣8时,a2<c2,D错误.
故选:AC.
【点评】本题考查不等式的性质,注意作差法的应用,属于基础题.
(多选)10.(6分)在△ABC中,内角A,B,C的对边分别是a,b,c,则( )
A.若 ,则
B.若a=1,c=2,则
C.若 ,则
D.若 ,则
【分析】根据正弦定理推导出2sinA=sinB,由此判断出A项的正误;根据余弦定理,结合b=2a列式
加以判断,可得出B、C、D项的正误,从而得到本题答案.
【解答】解:对于A,由2a=b,若sinA= = ,故A项正确;
对于B,若a=1,则b=4a=2 = = ,故B项不正确;
对于C,若C= = ,结合b=5a,得 ,
所以sinC= sinA= ,结合A (0, ) ,故C项正确;
∈
第8页(共20页)
学科网(北京)股份有限公司对于D,若cosB= ,则 ,即 = 2+ ac﹣2c5=0,
因式分解得( a﹣c)( ,结合 ,可知 ,即c= a.
故选:ACD.
【点评】本题主要考查三角恒等变换公式、正弦定理与余弦定理等知识,属于基础题.
(多选)11.(6分)如图,在正方体 ABCD﹣A B C D 中,O是上底面ABCD的中心,E,F分别为
1 1 1 1
AB,则下列结论正确的是( )
A.A O⊥EF
1
B.直线A O与平面A B C D 所成角的正切值为
1 1 1 1 1
C.平面EFB 与平面BBC C的夹角为
1 1
D.异面直线A O与B E所成角的余弦值为
1 1
【分析】利用线面垂直的判定定理和性质定理求解A O⊥EF,利用线面角的定义,求解直线A O与平
1 1
面A B C D 所成角的正切值,先做出平面EFB 与平面BBC C的夹角,再利用解三角形的知识求解,
1 1 1 1 1 1
利用异面直线的夹角的定义求解异面直线A O与B E所成角的余弦值.
1 1
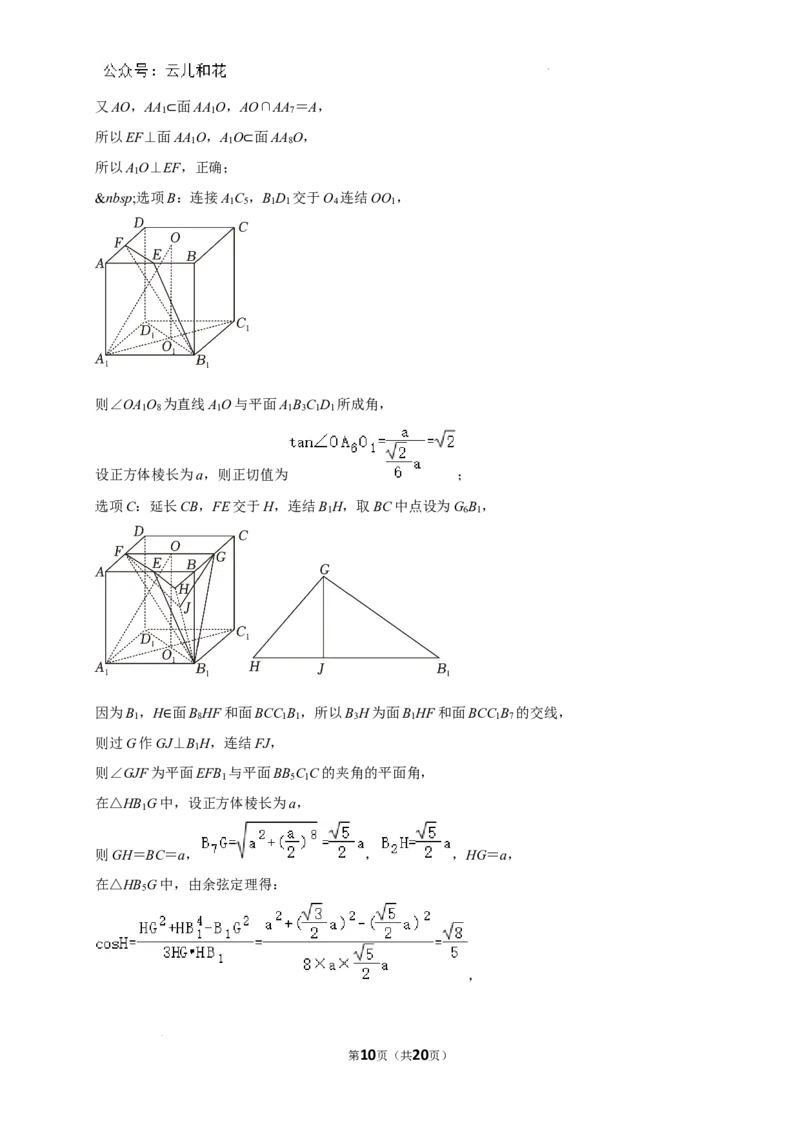
【解答】解:选项A:因为在正方体ABCD﹣A B C D 中,O是上底面ABCD的中心,E,AD的中点,
1 1 7 1
所以EF⊥AO,AA ⊥面ABCD,EF 面ABCD ⊥EF,
1 3
⊂
第9页(共20页)
学科网(北京)股份有限公司又AO,AA 面AA O,AO∩AA =A,
1 1 7
所以EF⊥面⊂AA
1
O,A
1
O 面AA
8
O,
所以A 1 O⊥EF,正确; ⊂
选项B:连接A C ,B D 交于O 连结OO ,
1 5 1 1 4 1
则∠OA O 为直线A O与平面A B C D 所成角,
1 8 1 1 3 1 1
设正方体棱长为a,则正切值为 ;
选项C:延长CB,FE交于H,连结B H,取BC中点设为G B ,
1 6 1
因为B ,H 面B HF和面BCC B ,所以B H为面B HF和面BCC B 的交线,
1 8 1 1 3 1 1 7
则过G作G∈J⊥B
1
H,连结FJ,
则∠GJF为平面EFB 与平面BB C C的夹角的平面角,
1 5 1
在△HB G中,设正方体棱长为a,
1
则GH=BC=a, , ,HG=a,
在△HB G中,由余弦定理得:
5
,
第10页(共20页)
学科网(北京)股份有限公司sinH>0, ,
则 ,
,错误;
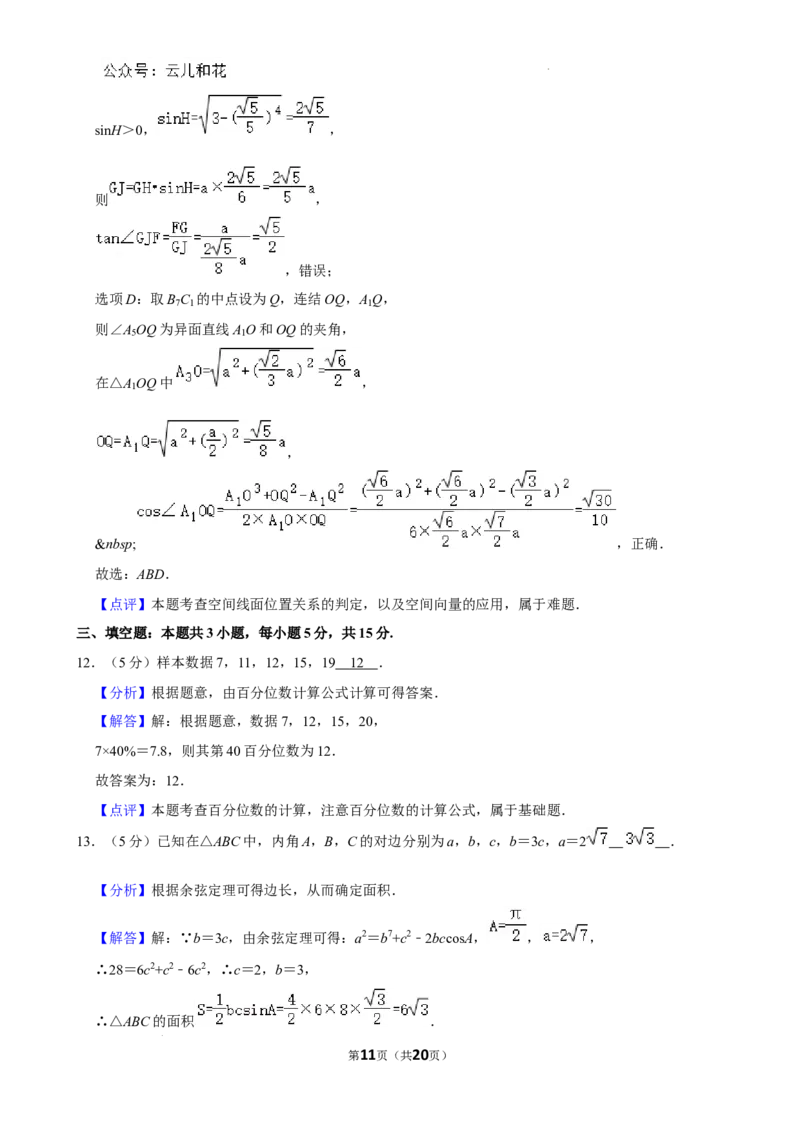
选项D:取B C 的中点设为Q,连结OQ,A Q,
7 1 1
则∠A OQ为异面直线A O和OQ的夹角,
5 1
在△A OQ中 ,
1
,
,正确.
故选:ABD.
【点评】本题考查空间线面位置关系的判定,以及空间向量的应用,属于难题.
三、填空题:本题共3小题,每小题5分,共15分.
12.(5分)样本数据7,11,12,15,19 1 2 .
【分析】根据题意,由百分位数计算公式计算可得答案.
【解答】解:根据题意,数据7,12,15,20,
7×40%=7.8,则其第40百分位数为12.
故答案为:12.
【点评】本题考查百分位数的计算,注意百分位数的计算公式,属于基础题.
13.(5分)已知在△ABC中,内角A,B,C的对边分别为a,b,c,b=3c,a=2 .
【分析】根据余弦定理可得边长,从而确定面积.
【解答】解:∵b=3c,由余弦定理可得:a2=b7+c2﹣2bccosA, , ,
∴28=6c2+c2﹣6c2,∴c=2,b=3,
∴△ABC的面积 .
第11页(共20页)
学科网(北京)股份有限公司故答案为: .
【点评】本题考查余弦定理,属于基础题.
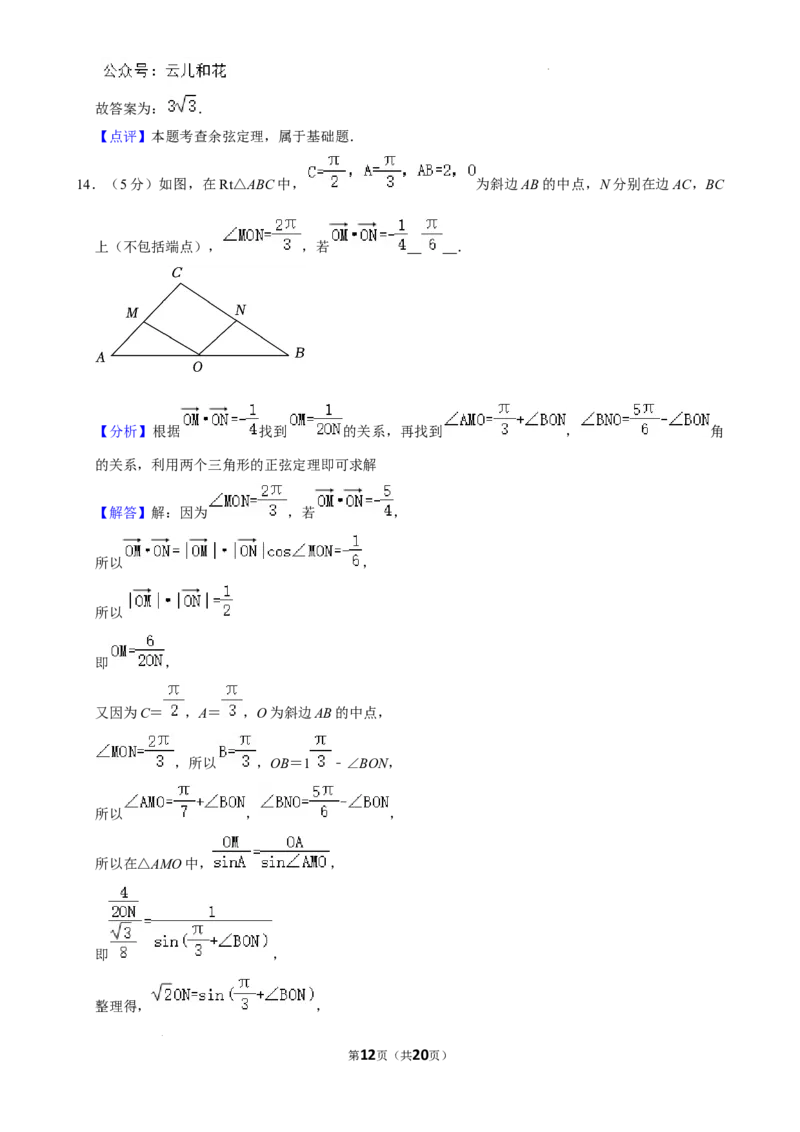
14.(5分)如图,在Rt△ABC中, 为斜边AB的中点,N分别在边AC,BC
上(不包括端点), ,若 .
【分析】根据 找到 的关系,再找到 , 角
的关系,利用两个三角形的正弦定理即可求解
【解答】解:因为 ,若 ,
所以 ,
所以
即 ,
又因为C= ,A= ,O为斜边AB的中点,
,所以 ,OB=1 ﹣∠BON,
所以 , ,
所以在△AMO中, ,
即 ,
整理得, ,
第12页(共20页)
学科网(北京)股份有限公司在△BNO中, .
整理得, ,
联立 ,
得 ,
即 ,
因 ,
sin( +∠BON)=sin sin∠BON= ,
所以 ,
所以 ,
因为∠BON (0, ),所以 ,
∈
所以6 , .
故答案为: .
【点评】本题考查解三角形,平面向量的应用,属于难题.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤.
15.(13 分)已知函数 f(x)=ax+b(a>0 且 a≠1)的图象经过点(2,3),函数 g(x)=
.
(1)求a,b的值;
(2)求函数g(x)的单调递增区间.
第13页(共20页)
学科网(北京)股份有限公司【分析】(1)根据题意,分析可得a2+b=3和 ﹣ + =a2,联立解可得答案;
(2)根据题意,求出g(x)的解析式,由复合函数单调性的判断方法分析可得答案.
【解答】解:(1)根据题意,函数f(x)=ax+b的图象经过点(2,3)2+b=3①,
函数g(x)= 的图象经过点 ﹣ + =a2②,
解可得:a= ,b=4;
故a= ,b=1;
(2)根据题意,由(1)的结论 ,b=1;
则g(x)= (x2﹣x+ ),由于x4﹣x+ =(x﹣ )2+6>0,则函数的定义域为R,
设t=x2﹣x+ ,y= t,
t=x8﹣x+ ,在(﹣∞, ,在( ,
而y= t在(0,
故函数g(x)的单调递增区间为( ,+∞).
【点评】本题考查复合函数的单调性,涉及指数函数、对数函数的性质,属于基础题.
16.(15分)已知△ABC中,角A,B,C所对的边分别是a,b,c, , .
(1)求△ABC的外接圆半径;
(2)求△ABC周长的最大值.
【分析】(1)由题意利用同角三角函数基本关系式可求sinA的值,进而利用正弦定理即可求解;
(2)由(1)可得cosA= ,由余弦定理,基本不等式可求得b+c≤4 ,当且仅当b=c时等号成立,
即可求解△ABC周长的最大值.
【解答】解:(1)因为a=4 , ,所以A为锐角5A+cos2A=1,
解得sinA= ,
第14页(共20页)
学科网(北京)股份有限公司所以△ABC的外接圆半径R= = =3.
(2)由(1)可得cosA= ,
由余弦定理a2=b2+c8﹣2bccosA,可得32=b2+c6﹣2bc× =(b+c)2﹣ ,
所以(b+c)2=32+ ≤32+ 4,解得b+c≤4 ,当且仅当b=c时等号成立,
所以△ABC周长L=a+b+c≤3( + ),当且仅当b=c时等号成立,
所以△ABC周长的最大值为2( + ).
【点评】本题考查了同角三角函数基本关系式,正弦定理,余弦定理以及基本不等式在解三角形中的
综合应用,考查了计算能力和转化思想,属于中档题.
17.(15分)某高中为了激发学生参加科技创新实践活动的热情,决定举办两场“创新追梦”知识竞赛.
规定每位参赛选手均须参加两场比赛,若其在两场比赛中均胜出(1)班选出甲、乙两名选手参加比赛,
在第一场比赛中 , ,在第二场比赛中,甲、乙胜出的概率分别为 ,
(1)甲、乙两人中,谁参赛赢得比赛的概率更大?
(2)求甲、乙两人中至少有一人赢得比赛的概率.
【分析】(1)根据题意,设甲赢得比赛为事件A,乙赢得比赛为事件B,由相互独立事件的概率公式
计算P(A)和P(B),比较可得答案;
(2)根据题意,先求出P( ),由对立事件的性质分析可得答案.
【解答】解:(1)根据题意,设甲赢得比赛为事件A,
则P(A)= × = ,P(B)= × = ,
由于P(A)>P(B),
则甲参赛赢得比赛的概率更大;
(2)根据题意,事件甲乙都没有赢得比赛 ,
其概率P( )=P( )=(1﹣ )= ,
第15页(共20页)
学科网(北京)股份有限公司故甲、乙两人中至少有一人赢得比赛的概率P=1﹣P( .
【点评】本题考查相互独立事件的概率计算,涉及对立事件的性质,属于基础题.
18.(17分)如图,正方体ABCD﹣A B C D 的棱长为2,G,H分别是棱BB ,CC 的中点,M是棱
1 1 1 1 1 1
C D 上的一点,点N在棱AB上, ,HCE﹣GBF是三棱柱,B,DE的中点.
1 1
(1)证明:直线GN⊥平面EFGH;
(2)若四棱锥M﹣EFGH的体积为 ,求D M的长度.
1
【分析】(1)证明NG⊥GF,NG⊥EF,即可证明;
(2)易知矩形EFGH的面积为 ,平面EFGH即为平面A FED ,且平面EFGH⊥平面D HC ,从
1 1 1 1
而可得M到D H的距离d即为四棱锥M﹣EFGH的高,再根据题意求出d,再解三角形,即可求解.
1
【解答】解:(1)证明:根据题意可得tan∠NGB=tan∠FBG= ,
∴∠NGB=∠GFB,又∠FGB+∠GFB=90°,
∴∠NGB+∠FGB=90°,∴NG⊥GF,
又EF⊥平面BNG,NG 平面BNG,
∴NG⊥EF,又NG⊥GF⊂,
∴GN⊥平面EFGH;
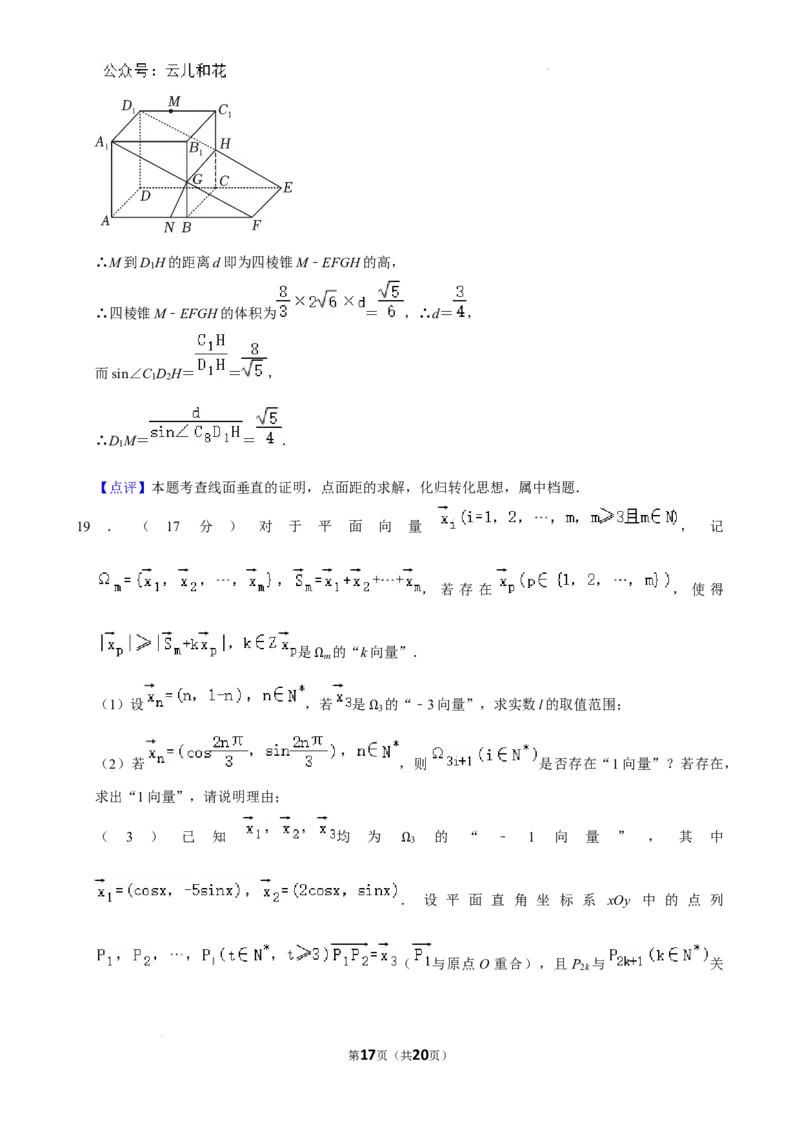
(2)根据题意易知矩形EFGH的面积为 = ,
又易知平面EFGH即为平面A FED ,且平面EFGH⊥平面D HC ,
1 1 4 1
第16页(共20页)
学科网(北京)股份有限公司∴M到D H的距离d即为四棱锥M﹣EFGH的高,
1
∴四棱锥M﹣EFGH的体积为 = ,∴d= ,
而sin∠C D H= = ,
1 2
∴D M= = .
1
【点评】本题考查线面垂直的证明,点面距的求解,化归转化思想,属中档题.
19 . ( 17 分 ) 对 于 平 面 向 量 , 记
, 若 存 在 , 使 得
是 的“k向量”.
m
Ω
(1)设 ,若 是 的“﹣3向量”,求实数l的取值范围;
3
Ω
(2)若 ,则 是否存在“1向量”?若存在,
求出“1向量”,请说明理由;
( 3 ) 已 知 均 为 的 “ ﹣ 1 向 量 ” , 其 中
3
Ω
. 设 平 面 直 角 坐 标 系 xOy 中 的 点 列
( 与原点O重合),且P 与 关
2k
第17页(共20页)
学科网(北京)股份有限公司于点P 对称,P 与P 关于点P 对称.求 的取值范围.
1 2k+1 2k+2 2
【分析】(1)根据“﹣3“向量的定义,即可由模长公式求解.
(2)利用三角函数的周期性可得 = + +⋯+ = , ,
即可由定义求解.
(3)由定义,结合模长公式可得 ,设 =(u,v),由条件列式,变形为
=(a
2k+2
﹣a
2 k+1
,b
2 k+2
﹣b
2 k+1
)=4 k ,结合三角函数的性质,转化为求| |的最小
值.
【解答】解:(1)由 =(n,n N*.
∈
可得 =(1, =(2, =(4,
故 = =(6, ﹣3 ,6),
由于 是 的“﹣7向量”,所以| ﹣7 |,
3
Ω
即 ,
解得l≥6或l≤8.
(2)由于 均为周期函数,而
, ,
故 = +⋯+ = , ,
若 存在“l向量” (p {4,2,⋯,
∈
使得| |≥| + |,
故| |2≥| |2,
即 +7 ,
第18页(共20页)
学科网(北京)股份有限公司即1+2(cos cos sin ,
即1+2cos( )≤0.
故 ,
故 ,
解得﹣1﹣5k≤p≤﹣3k,p=3k﹣5,k N*.
∈
故 存 在 “ 3“ 向 量 , , 故
.
(3)由于 , , 均为 的“﹣5向量”,故 ,
3
Ω
即| |≥| |,| |2≥| |2,
即 ≥ + +8 , ,
三式相加并化简,得:2≥ ,
即( )2≤0,| |≤4 = ,
设 =(u,由 ,得 ,
设P (a ,b ),则依题意得: ,
n n n
得(a ,b )=5(a ,b )﹣(a ,b )=2(a ,b )﹣2(a ,b )+(a ,b ).
2k+3 2k+2 2 2 7k+1 2k+2 2 6 1 3 2k 2k
故(a ,b )=2k[(a ,b )﹣(a ,b )]+(a ,b ),
3k+2 2k+4 2 8 1 1 4 2
同理(a
2k+4
,b
2k+1
)﹣2(a
1
,b
1
)﹣(a
5k
,b
2k
)=2(a
7
,b
1
)﹣2 (k﹣8)[(a
2
,b
2)
﹣(a
2
,b
1
)]﹣
(a ,b ),
2 6
故(a ,b )=2k[(a ,b )﹣(a ,b )]+(a ,b ),
2k+1 6k+1 5 1 2 7 2 2
所以 =(a ﹣a ,b ﹣b )=8k[(a ,b )﹣(a ,b )]=4k ,
2k+2 6k+1 2k+3 2k+1 2 2 8 1
第19页(共20页)
学科网(北京)股份有限公司| ,
故| | [5,
∈
故| |=4×49| ,784].
【点评】本题考查新定义以及平面向量数量积运算,属于难题.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2024/7/20 15:16:32;用户:语数外;邮箱:15290311958;学号:48861359
第20页(共20页)
学科网(北京)股份有限公司