文档内容
格致课堂
6.4.1 平面几何中的向量方法
(用时45分钟)
基础巩固
1.已知 是坐标平面上的三点,其坐标分别为 ,则 的形状
为( )
A.直角(非等腰)三角形 B.等腰(非等边)三角形
C.等腰直角三角形 D.以上均不正确
2.在△ABC中,若 ,则 的形状为( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不确定
3.设点M是线段BC的中点,点A在直线BC外, ,则 ( )
A.8 B.4 C.2 D.1
4.若 ,且 ,则四边形 是( )
A.平行四边形 B.菱形 C.等腰梯形 D.非等腰梯形
5.在平行四边形 中, , , 为 的中点,若 ,则 的长为
( )
A.1 B. C. D.
6.设点O是三角形ABC所在平面上一点,若 ,则点O是三角形ABC的________心.
7.设 是△ABC内部一点,且 ,则△AOB与 的面积之比为
________________.
8.求证:以 为顶点的四边形是一个矩形.格致课堂
能力提升
9.平行四边形 中, , 点P在边CD上,则 的取值范围是(
)
A.[-1,8] B. C.[0,8] D.[-1,0]
10.已知 为△ 的外心,若 + − =0,则 =_____.
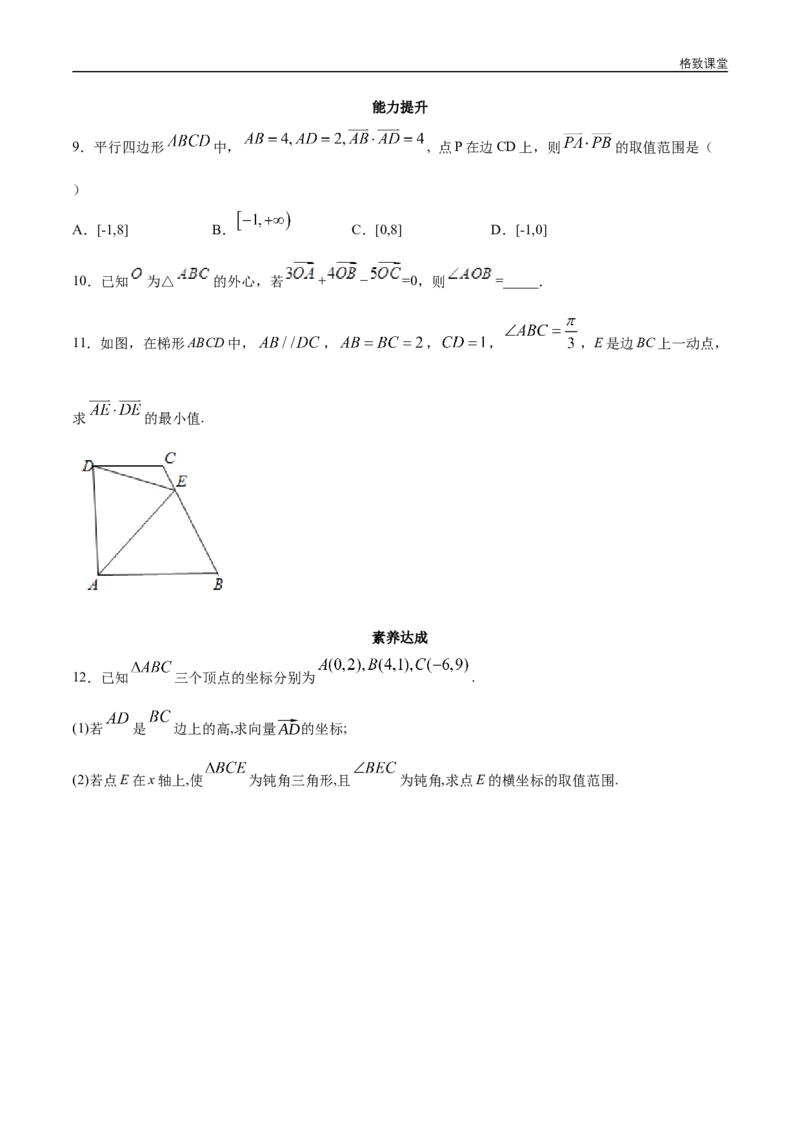
11.如图,在梯形ABCD中, , , , ,E是边BC上一动点,
求 的最小值.
素养达成
12.已知 三个顶点的坐标分别为 .
(1)若 是 边上的高,求向量⃗AD的坐标;
(2)若点E在x轴上,使 为钝角三角形,且 为钝角,求点E的横坐标的取值范围.