文档内容
格致课堂
8.6.3 平面与平面垂直
第 2 课时 平面与平面垂直的性质
一、选择题
1.设 , 是两个不同的平面, , 是两条不同的直线,且 , ( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
【答案】A
【解析】
试题分析:由面面垂直的判定定理:如果一个平面经过另一平面的一条垂线,则两面垂直,可得 ,
可得
2.如图所示,在平行四边形 中, ,沿 将 折起,使平面 平面 ,
连接 ,则在四面体 的四个面中,互相垂直的平面的对数为( )
A.1 B.2 C.3 D.4
【答案】C
【解析】
∵面ABD⊥面BCD,AB⊥BD,∴AB⊥面BCD,又AB 面ABC,
∴面ABC⊥面BCD,同理,面ACD⊥面ABD. ⊂
故四面体ABCD中互相垂直的平面有3对.格致课堂
3.如图所示,三棱锥 的底面在平面 内,且 ,平面 平面 ,点
是定点,则动点 的轨迹是( )
A.一条线段 B.一条直线 C.一个圆 D.一个圆,但要去掉两个点
【答案】D
【解析】
因为平面PAC⊥平面PBC,AC⊥PC,平面PAC∩平面PBC=PC,
AC 平面PAC,所以AC⊥平面PBC.
又因⊂为BC 平面PBC,所以AC⊥BC.所以∠ACB=90°.
所以动点C⊂的轨迹是以AB为直径的圆,除去A和B两点.
选D.
4.已知平面 平面 , ,点 , ,直线 ,直线 ,直线 ,
,则下列四种位置关系中,不一定成立的是( )
A. B. C. D.
【答案】D
【解析】如图所示:
由于 , , ,所以 ,又因为 ,所以 ,故A正确,
由于 , ,所以 ,故B正确,格致课堂
由于 , , 在 外,所以 ,故C正确;
对于D,虽然 ,当 不一定在平面 内,故它可以与平面 相交、平行,不一定垂直,所以D
不正确;
故答案选D
5.(多选题)给定下列四个命题:
A.若一个平面内的两条直线与另一个平面都平行,则这两个平面相互平行;
B.若一个平面经过另一个平面的垂线,则这两个平面相互垂直;
C.垂直于同一直线的两条直线相互平行;
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④
【答案】BD
【解析】当两个平面相交时,一个平面内的两条直线也可以平行于另一个平面,故A错误;由平面与平面
垂直的判定可知B正确;空间中垂直于同一条直线的两条直线还可以相交或者异面,故C错误;若两个平
面垂直,只有在一个平面内与它们的交线垂直的直线才与另一个平面垂直,故D正确.综上,真命题是
BD.
故选:BD
6.(多选题)如图所示,在直角梯形 中, , 分别是 上的点,
,且 (①).将四边形 沿 折起,连接 (②).在折起
的过程中,下列说法中正确的是( )
A. 平面格致课堂
B. 四点不可能共面
C.若 ,则平面 平面
D.平面 与平面 可能垂直
【答案】ABC
【解析】选项A中,连接 ,取 的中点 , 的中点 ,
连接 , 且 ,
而 且 ,
所以 且
所以四边形 是平行四边形,
所以 ,而 平面 , 平面 ,
所以 平面 ,
所以A正确;
选项B中,设 四点共面,
因为 , 平面 , 平面 ,
所以 平面 ,
而 平面 ,平面 平面 ,
所以 ,
所以 ,这与已知相矛盾,
故 四点不可能共面,
所以B正确;
选项C中,连接 ,格致课堂
在梯形 中,易得 ,
又 , 平面 , ,
所以 平面
而 平面 ,所以 ,
而 , 平面 ,且 与 必有交点,
所以 平面 ,
因为 平面 ,
所以平面 平面 ,
所以C正确;
选项D中,延长 至 ,使得 ,连接 ,
, , 平面 , ,
所以 平面 ,
而 ,所以 平面 ,
因为 平面 ,所以平面 平面 ,
过 作 于 , 平面 ,平面 平面 ,
所以 平面 ,
若平面 平面 ,
则过 作直线与平面 垂直,其垂足在 上,
故前后矛盾,
所以D错误.
故选:ABC.
二、填空题格致课堂
7.如图,四面体 中, ,平面 平面 , ,
,则 _______.
【答案】13
【解析】
取 的中点 ,连接 .
因为 , ,所以 ,所以 .
因为 , 是 的中点,所以 .
因为平面 平面 ,平面 平面 , 平面 ,
所以 平面 .
因为 平面 ,所以 .
在 中, .
8.如图所示, 为空间四点,在 中, ,等边三角形
以 为轴运动,当平面 平面 时, ________.格致课堂
【答案】2.
【解析】取 的中点 ,连接 .因为 是等边三角形,所以 .当平面 平
面 时,因为平面 平面 ,且 ,所以 平面 ,故 .由已
知可得 ,在 中, .
9.平面 平面 , , , ,直线 ( , 是两条不同的直线),则直线
与 的位置关系是______.
【答案】
【解析】解:因为平面 平面 , , , ,
由面面垂直的性质可得 ,又 ,所以 .
故答案为:
10.已知PA⊥正方形ABCD所在的平面,垂足为A,连接PB,PC,PD,则平面PAB,平面PAD,平面
PCD,平面PBC,平面ABCD中,互相垂直的平面有 对.格致课堂
【答案】5
【解析】 ,又
, 同
理,平面 平面 ,平面 平面 ,所以互相垂直的平面共有5对.
三、解答题
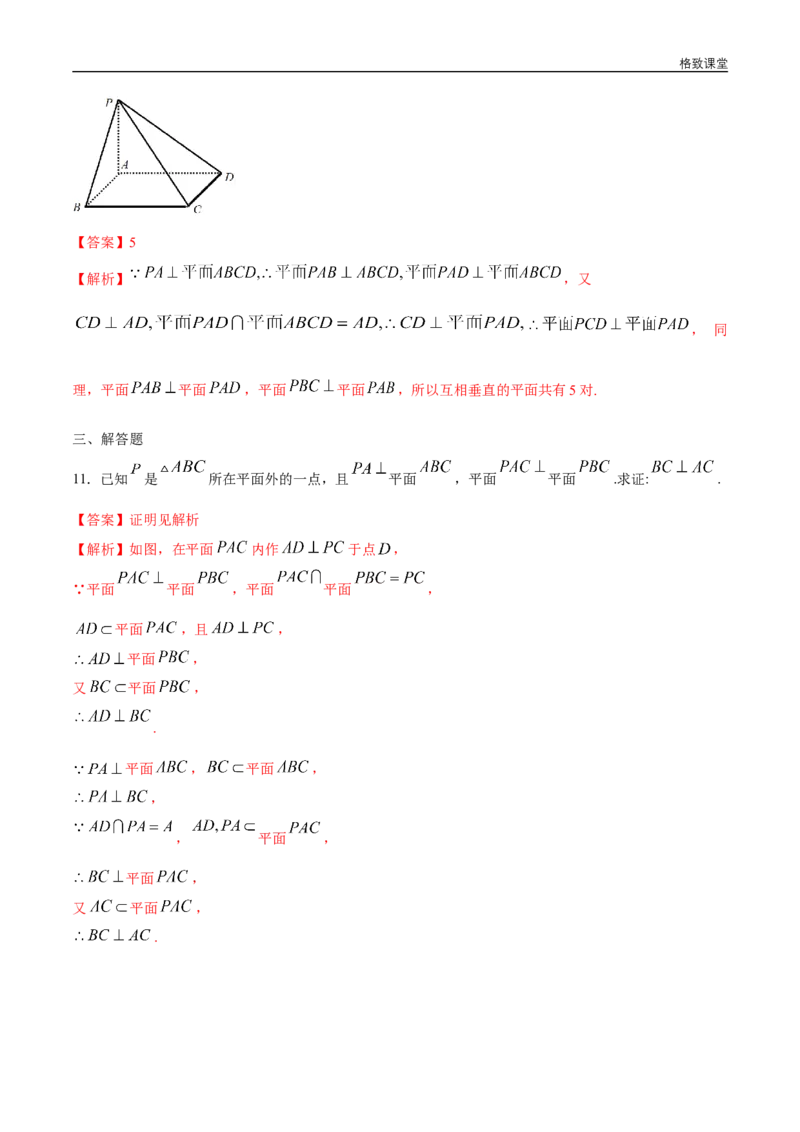
11.已知 是 所在平面外的一点,且 平面 ,平面 平面 .求证: .
【答案】证明见解析
【解析】如图,在平面 内作 于点 ,
∵平面 平面 ,平面 平面 ,
平面 ,且 ,
平面 ,
又 平面 ,
.
平面 , 平面 ,
,
, 平面 ,
平面 ,
又 平面 ,
.格致课堂
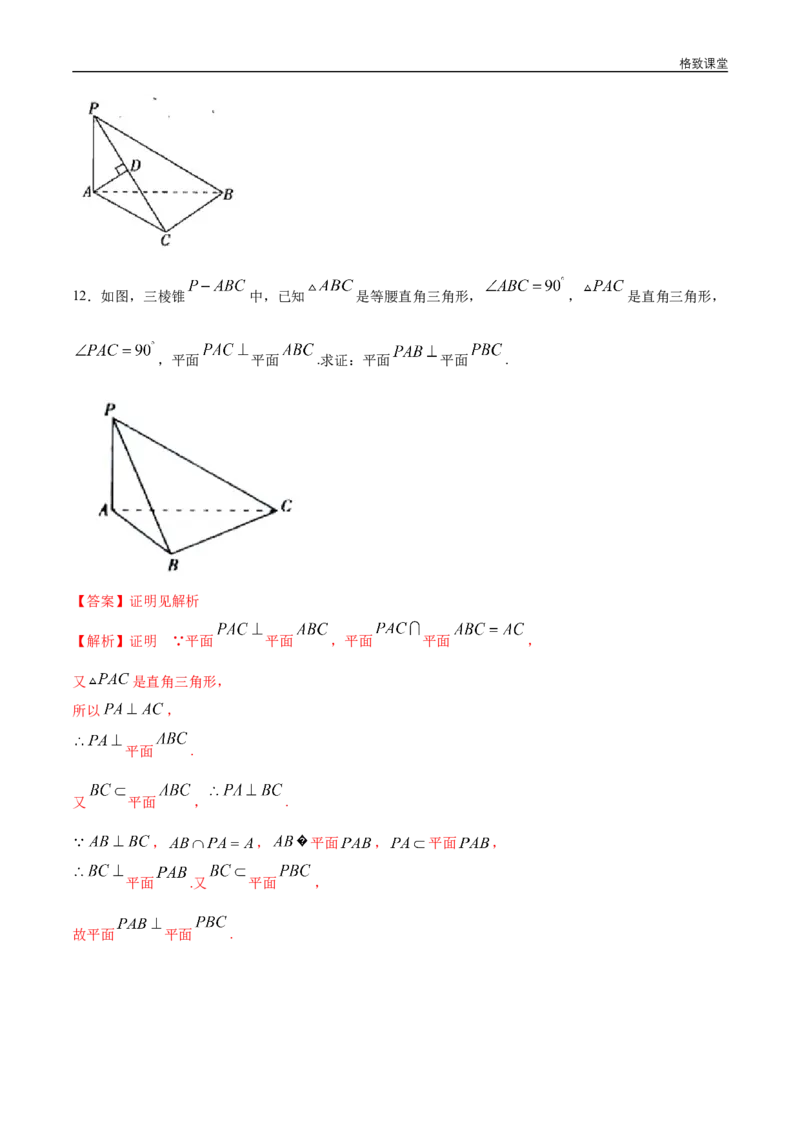
12.如图,三棱锥 中,已知 是等腰直角三角形, , 是直角三角形,
,平面 平面 .求证:平面 平面 .
【答案】证明见解析
【解析】证明 ∵平面 平面 ,平面 平面 ,
又 是直角三角形,
所以 ,
平面 .
又 平面 , .
, , 平面 , 平面 ,
平面 .又 平面 ,
故平面 平面 .