文档内容
学年上学期夏津⼀中⾼⼀年级 ⽉份⽉考
2025-2026 12
数学试题
⼀、单选题(每题5分,共8个题40分)
1. 是( )
A. 第⼀象限⻆ B. 第⼆象限⻆ C. 第三象限⻆ D. 第四象限⻆
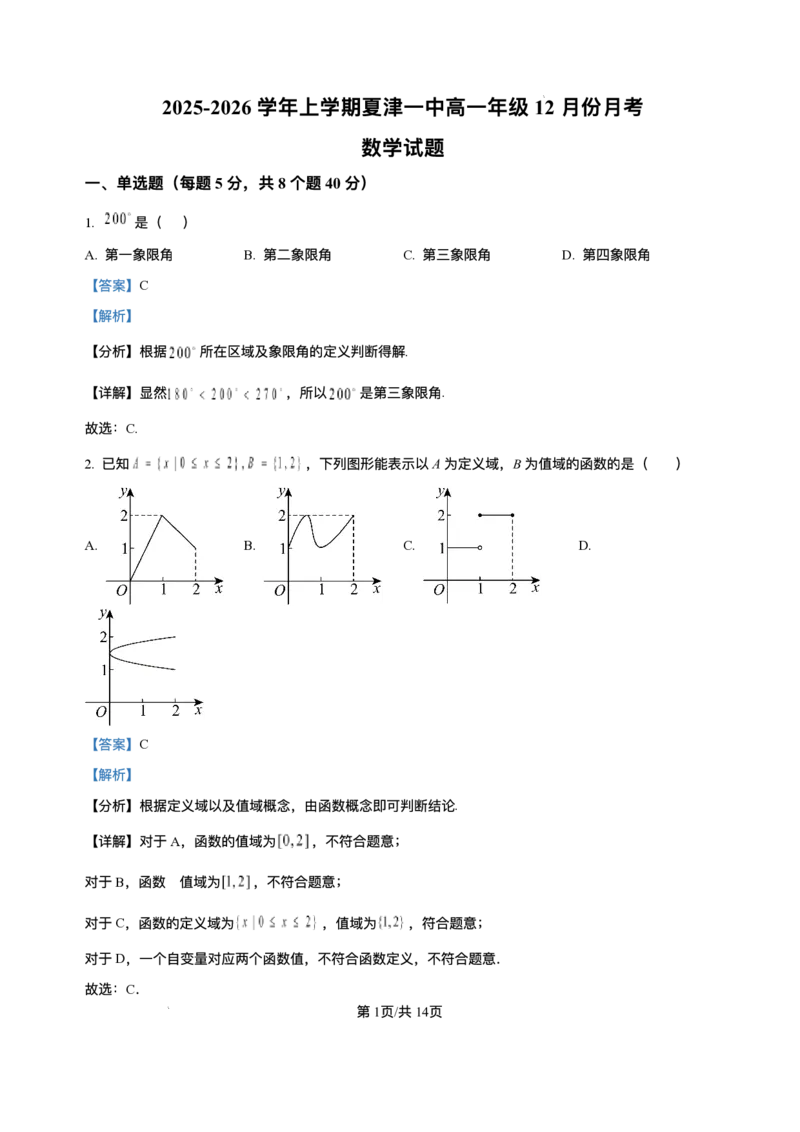
2. 已知 ,下列图形能表示以A为定义域,B为值域的函数的是( )
A B. C. D.
3. 若⻆ 始边与 轴的⾮负半轴重合,终边经过点 ,则 ( )
A. B. C. D.
4. 下列四个命题,其中为真命题的是( )
A. 若函数 在 上是增函数,在 上也是增函数,则 是增函数
B. 和 表示同⼀函数
C. 函数 的单调增区间为
D. 若函数 的值域是 ,则实数 或
5. 已知函数 ,记 , , ,则( )
A. B. C. D.
6. 已知幂函数 是 上的偶函数,且函数 在区间 上
第1⻚/共3⻚
学科⽹(北京)股份有限公司单调递减,则实数a的取值范围是( )
A. B. C. D.
7. 设 ,则“ ” 是“ ” ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 从盛有 纯酒精的容器中倒出 ,然后⽤⽔填满;再倒出 ,⼜⽤⽔填满……连续进⾏ 次后,容
器中纯酒精剩下不到 ,则 ⾄少是( )
A.4 B.5 C.6 D.7
⼆、多选题(每题6分,共3个题18分)
9. 下列结论正确的有( )
A.
B. 当 时,
C. 终边落在直线 上的⻆的集合是
D. 已知点 在第四象限,则⻆ 终边在第⼆象限
10. 下列结论正确的是( )
A. 函数 的定义域为
B. 若⻆ 的终边过点 ,则
C. 函数 图象关于原点对称
D. 若圆⼼⻆为 的扇形的弧⻓为 ,则该扇形⾯积为
11. 已知 , ,则下列关系中正确的是( )
A. B.
C. 若 ,则 的最⼩值为 D. 若 ,则
三、填空题(每题5分,共3个题15分)
12. 已知 ( 且 ),则 的取值范围是______.
第2⻚/共3⻚
学科⽹(北京)股份有限公司13. 若集合 有且只有两个元素,则实数a的取值范围是______.
14. 若函数 在 上为减函数,则a取值范围是___________.
四、解答题(共77分)
15. 计算以下各题
(1) ;
(2)
(3)
16. 已知函数 的定义域为 .
(1)求实数 取值集合 ;
(2)设 为⾮空集合,若 是 的必要不充分条件,求实数 的取值范围.
17. 已知函数 , .
(1)求函数 的定义域;
(2)判断函数 的奇偶性,并说明理由;
(3)求使得不等式 成⽴的 的取值范围.
18. 已知幂函数 在 上单调递增.
(1)求 的值;
(2)求关于 的不等式 的解集.
19. 已知 是定义在 上的奇函数, .
(1)求函数 在 上的解析式;
(2)若 ,都有 成⽴,求实数 的取值范围.
第3⻚/共3⻚
学科⽹(北京)股份有限公司学年上学期夏津⼀中⾼⼀年级 ⽉份⽉考
2025-2026 12
数学试题
⼀、单选题(每题5分,共8个题40分)
1. 是( )
A. 第⼀象限⻆ B. 第⼆象限⻆ C. 第三象限⻆ D. 第四象限⻆
【答案】C
【解析】
【分析】根据 所在区域及象限⻆的定义判断得解.
【详解】显然 ,所以 是第三象限⻆.
故选:C.
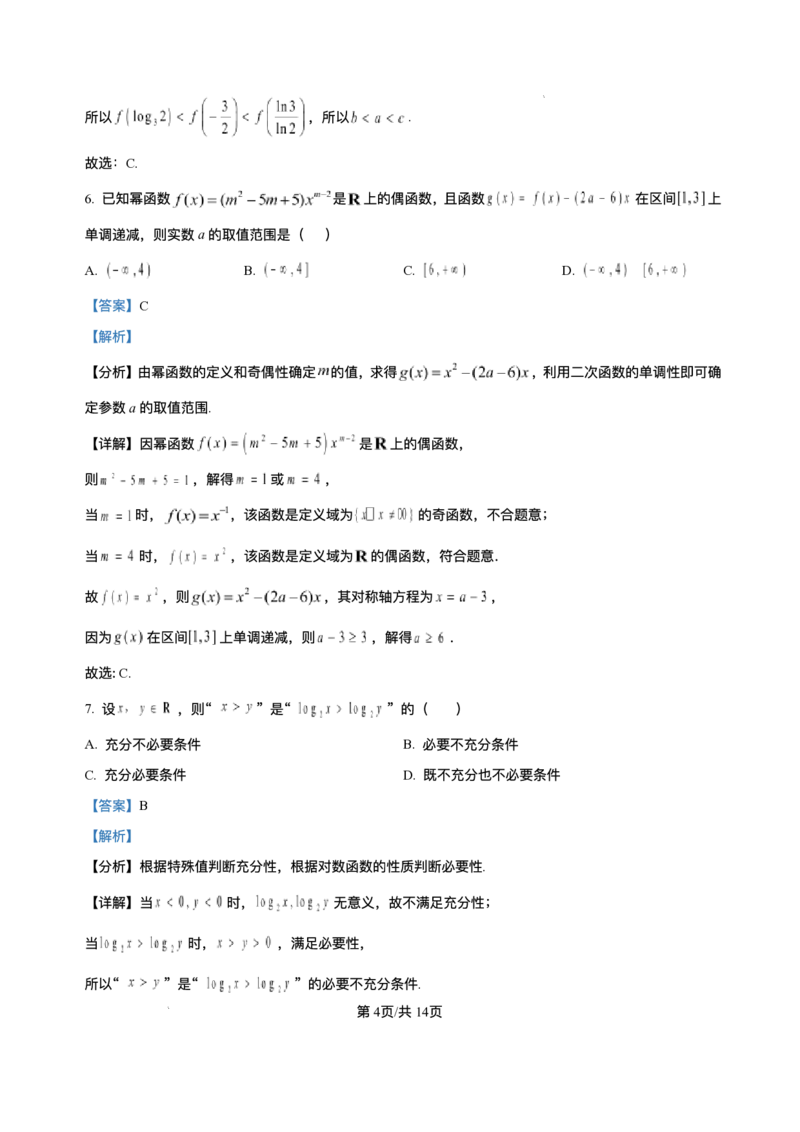
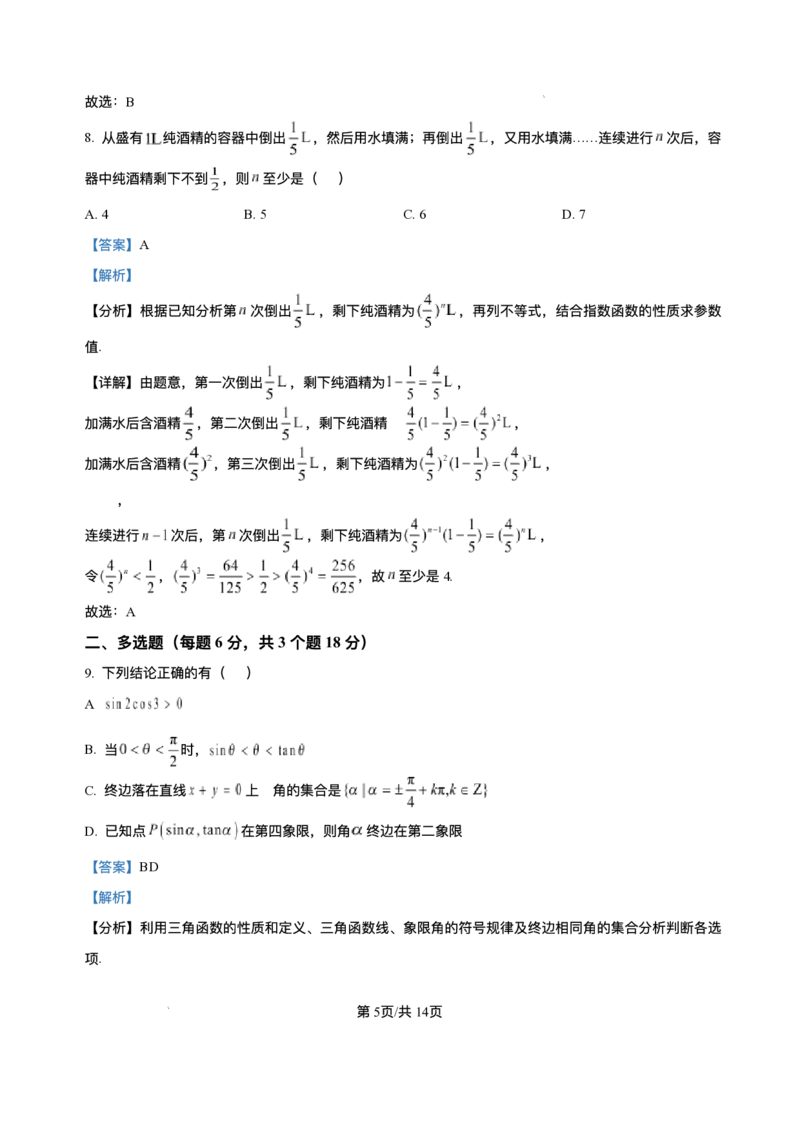
2. 已知 ,下列图形能表示以A为定义域,B为值域的函数的是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据定义域以及值域概念,由函数概念即可判断结论.
【详解】对于A,函数的值域为 ,不符合题意;
对于B,函数 值域为 ,不符合题意;
对于C,函数的定义域为 ,值域为 ,符合题意;
对于D,⼀个⾃变量对应两个函数值,不符合函数定义,不符合题意.
故选:C.
第1⻚/共14⻚
学科⽹(北京)股份有限公司3. 若⻆ 的始边与 轴的⾮负半轴重合,终边经过点 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】由条件利⽤任意⻆的三⻆函数的定义,求出 的值,可得 的值.
【详解】因为⻆ 的终边经过点 , , , ,
所以 ,
则 .
故选:C.
4. 下列四个命题,其中为真命题的是( )
A. 若函数 在 上是增函数,在 上也是增函数,则 是增函数
B. 和 表示同⼀函数
C. 函数 的单调增区间为
D. 若函数 的值域是 ,则实数 或
【答案】D
【解析】
【分析】对A,取 进⾏说明,即判断正误;对B,利⽤相同函数的判断⽅法,即可求解;对C,
直接求出 的增区间,即可判断正误;对D,利⽤⼆次函数的性质,结合条件得
.
【详解】对于A,取 ,易知 在 上是增函数,在 上也是增函数,
但 在 上不具有单调性,即 不是增函数,所以A错误,
对于B,因为 的值域为 , 的值域为 ,所以 和 不表示
第2⻚/共14⻚
学科⽹(北京)股份有限公司同⼀函数,故B错误,
对于C,因为 ,
当 时, ,对称轴为 ,图象开⼝向上,在区间 上单调递减,在区间
上单调递增,
当 时, ,对称轴为 ,图象开⼝向上,在区间 上单调递增,在区间
上单调递减,
所以 的单调增区间为 , ,故C错误,
对于D,函数 的值域是 ,⼜ 的对称轴为 ,图
象开⼝向上,
则 ,解得 或 ,所以D正确,
故选:D.
5. 已知函数 ,记 , , ,则( )
A. B. C. D.
【答案】C
【解析】
【分析】先判断函数 为偶函数,且在 上单调递增,运⽤对数的运算,将三个⾃变量化简到
内,最后利⽤单调性、奇偶性⽐较⼤⼩.
【详解】因为函数 ,定义域为 ,⽽且
所以 为偶函数,
因为 时, 在 上单调递增;
,
因为 ,所以 ,
第3⻚/共14⻚
学科⽹(北京)股份有限公司所以 ,所以 .
故选:C.
6. 已知幂函数 是 上的偶函数,且函数 在区间 上
单调递减,则实数a的取值范围是( )
A. B. C. D.
【答案】C
【解析】
【分析】由幂函数的定义和奇偶性确定 的值,求得 ,利⽤⼆次函数的单调性即可确
定参数a的取值范围.
【详解】因幂函数 是 上的偶函数,
则 ,解得 或 ,
当 时, ,该函数是定义域为 的奇函数,不合题意;
当 时, ,该函数是定义域为 的偶函数,符合题意.
故 ,则 ,其对称轴⽅程为 ,
因为 在区间 上单调递减,则 ,解得 .
故选:C.
7. 设 ,则“ ” 是“ ” 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】B
【解析】
【分析】根据特殊值判断充分性,根据对数函数的性质判断必要性.
【详解】当 时, ⽆意义,故不满⾜充分性;
当 时, ,满⾜必要性,
所以“ ” 是“ ” 的必要不充分条件.
第4⻚/共14⻚
学科⽹(北京)股份有限公司故选:B
8. 从盛有 纯酒精的容器中倒出 ,然后⽤⽔填满;再倒出 ,⼜⽤⽔填满……连续进⾏ 次后,容
器中纯酒精剩下不到 ,则 ⾄少是( )
A.4 B.5 C.6 D.7
【答案】A
【解析】
【分析】根据已知分析第 次倒出 ,剩下纯酒精为 ,再列不等式,结合指数函数的性质求参数
值.
【详解】由题意,第⼀次倒出 ,剩下纯酒精为 ,
加满⽔后含酒精 ,第⼆次倒出 ,剩下纯酒精 ,
加满⽔后含酒精 ,第三次倒出 ,剩下纯酒精为 ,
,
连续进⾏ 次后,第 次倒出 ,剩下纯酒精为 ,
令 , ,故 ⾄少是4.
故选:A
⼆、多选题(每题6分,共3个题18分)
9. 下列结论正确的有( )
A
B. 当 时,
C. 终边落在直线 上 ⻆的集合是
D. 已知点 在第四象限,则⻆ 终边在第⼆象限
【答案】BD
【解析】
【分析】利⽤三⻆函数的性质和定义、三⻆函数线、象限⻆的符号规律及终边相同⻆的集合分析判断各选
项.
第5⻚/共14⻚
学科⽹(北京)股份有限公司【详解】对于A, ,
, , ,故A错误;
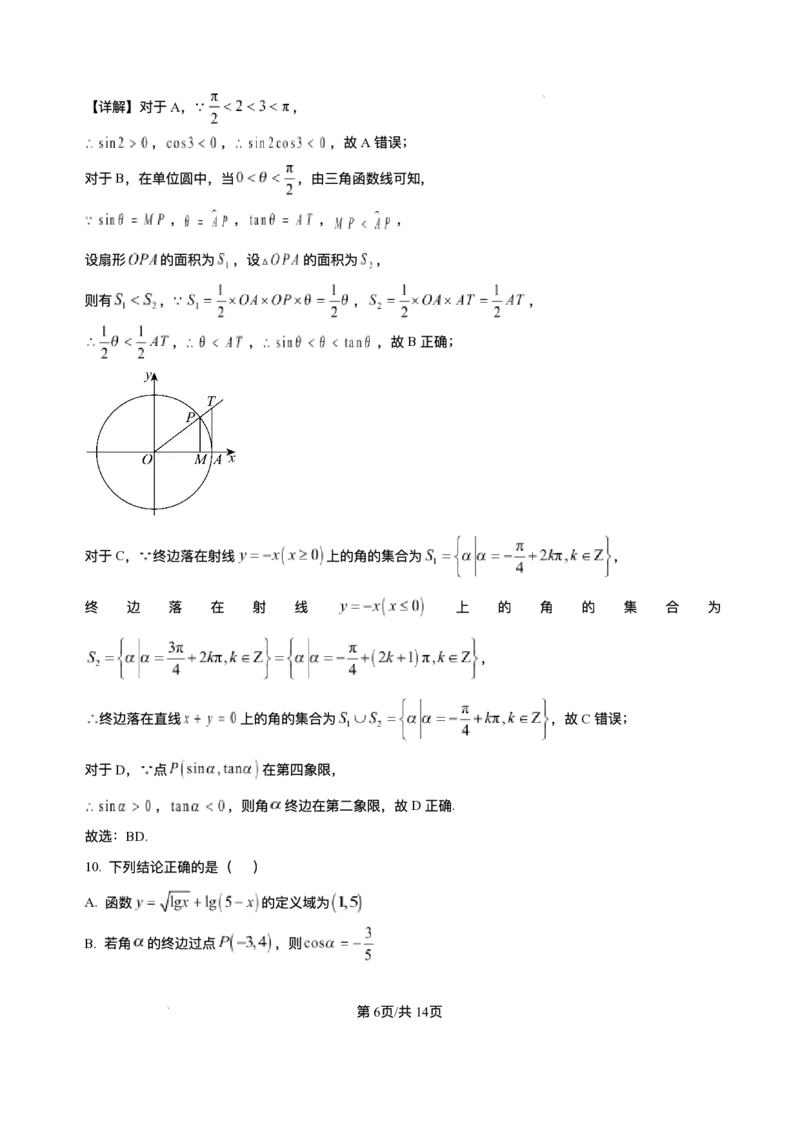
对于B,在单位圆中,当 ,由三⻆函数线可知,
, , , ,
设扇形 的⾯积为 ,设 的⾯积为 ,
则有 , , ,
, , ,故B正确;
对于C, 终边落在射线 上的⻆的集合为 ,
终 边 落 在 射 线 上 的 ⻆ 的 集 合 为
,
终边落在直线 上的⻆的集合为 ,故C错误;
对于D, 点 在第四象限,
, ,则⻆ 终边在第⼆象限,故D正确.
故选:BD.
10. 下列结论正确的是( )
A. 函数 的定义域为
B. 若⻆ 的终边过点 ,则
第6⻚/共14⻚
学科⽹(北京)股份有限公司C. 函数 的图象关于原点对称
D. 若圆⼼⻆为 的扇形的弧⻓为 ,则该扇形⾯积为
【答案】BCD
【解析】
【分析】对A,根据函数解析式求出定义域判断;对B,根据三⻆函数定义求解判断;对C,根据函数奇偶
性定义求解判断;对D,根据扇形的弧⻓和⾯积公式求解.
【详解】对于A,由题可得 ,解得 ,故函数 的定义域为 ,故A错误;
对于B,因为⻆ 的终边经过点 ,所以 ,故B正确;
对于C,由 ,解得 ,
⼜ ,
所以 为奇函数,图象关于原点对称,故C正确;
对于D,设扇形的半径为 ,则 ,解得 ,
所以扇形的⾯积 ,故D正确.
故选:BCD.
11. 已知 , ,则下列关系中正确的是( )
A. B.
C. 若 ,则 的最⼩值为 D. 若 ,则
【答案】ACD
【解析】
【分析】
对式⼦变形,然后逐⼀判断是否具备“⼀正⼆定三相等”的条件,求最值;
【详解】因为 , ,所以 ,所以 ,所以
第7⻚/共14⻚
学科⽹(北京)股份有限公司,故A正确;
因为 和 不⼀定是正实数,故不可⽤基本不等式,从⽽ 不⼀定正确,故B
错误;
若 ,则
,故C正确;
因为 ,所以 ,所以 ,当且仅当
时等号成⽴,故D正确.
故选:ACD.
【点睛】在应⽤基本不等式求最值时,要把握不等式成⽴的三个条件,就是“⼀正——各项均为正;⼆定
——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.对于公式
,要弄清它们的作⽤、使⽤条件及内在联系,两个公式也体现了ab和a+b
的转化关系.
三、填空题(每题5分,共3个题15分)
12. 已知 ( 且 ),则 的取值范围是______.
【答案】
【解析】
【分析】把 变形为 ,然后对 和 讨论,得出结果
【详解】因为 ,所以 ,
当 时, ,所以 ,
第8⻚/共14⻚
学科⽹(北京)股份有限公司当 时, ,所以 ,
所以 的取值范围是 ,
故答案为:
13. 若集合 有且只有两个元素,则实数a的取值范围是______.
【答案】
【解析】
【分析】先将不等式左边分解因式,然后根据零点⼤⼩关系分类讨论.
【详解】因为 ,
当 时, ,正整数解不可能有两个;
当 时, ;
当 时, ,要满⾜有两个正整数解﹐则 .
综上,实数 的取值范围为 .
故答案为:
14. 若函数 在 上为减函数,则a取值范围是___________.
【答案】
【解析】
【分析】令 , 且 , ,由 是增函数且 恒成⽴,列出关于
的不等式组并解之即可.
【详解】令 , 且 , ,
因为函数 在 上是减函数且 在 上是减函数,
所以 是增函数且 恒成⽴,
第9⻚/共14⻚
学科⽹(北京)股份有限公司即 ,解之得 的取值范围是 .
故答案为: .
四、解答题(共77分)
15. 计算以下各题
(1) ;
(2)
(3)
【答案】(1)84 (2)0
(3)
【解析】
【分析】(1)根据指数的运算法则及性质求解;
(2)根据对数的运算法则及性质计算得解;
(3)根据特殊⻆的三⻆函数值计算即可.
【⼩问1详解】
.
【⼩问2详解】
.
【⼩问3详解】
.
16. 已知函数 的定义域为 .
(1)求实数 的取值集合 ;
第10⻚/共14⻚
学科⽹(北京)股份有限公司(2)设 为⾮空集合,若 是 的必要不充分条件,求实数 的取值范围.
【答案】(1) ;(2) .
【解析】
【分析】(1)由题意可知, 在 上恒成⽴,再对参数 进⾏分类讨论,根据⼆次函数的性
质,即可求出结果;
(2)由命题的关系与集合间的包含关系得: 是 的必要不充分条件,所以 ,由此列出关系
式,即可求出结果.
【详解】(1)可知, 在 上恒成⽴,
当 时, ,成⽴;
当 时, ,解得 ;
综上所述, . 所以集合
(2)因为, 是 的必要不充分条件. 所以,
故 ,解得
所以,实数 的取值范围是 .
17. 已知函数 , .
(1)求函数 的定义域;
(2)判断函数 的奇偶性,并说明理由;
(3)求使得不等式 成⽴的 的取值范围.
【答案】(1)
(2)奇函数,理由⻅解析
(3)
【解析】
【分析】(1)根据对数函数的概念求定义域即可.
(2)根据奇函数的定义进⾏判断即可.
第11⻚/共14⻚
学科⽹(北京)股份有限公司(3)根据对数函数的性质求不等式的解集即可.
【⼩问1详解】
因为函数 ,
所以 .
要使得其有意义,则 ,解得 .
所以函数 的定义域为 .
【⼩问2详解】
因为函数 的定义域为 ,关于原点对称,
且 ,所以
所以函数 为奇函数.
【⼩问3详解】
因为 ,所以 ,
所以 ,化简得 ,解得 .
所以不等式 解集为 .
18. 已知幂函数 在 上单调递增.
(1)求 的值;
(2)求关于 的不等式 的解集.
【答案】(1)3 (2)答案⻅解析
【解析】
【分析】(1)根据幂函数的概念,结合 时,幂函数在 上单调递增即可解题;
(2)根据⼀元⼆次不等式的解集的求法,对 分类讨论,即可求解.
第12⻚/共14⻚
学科⽹(北京)股份有限公司【⼩问1详解】
因为函数 为幂函数,
所以 ,解得 或 .
当 时, ,在 上单调递增,符合题意;
当 时, ,在 上单调递减,不符合题意;
所以 .
【⼩问2详解】
由(1)知 ,由 ,
得 .
当 ,即 时,不等式 ⽆解;
当 ,即 时,不等式 解为 ;
当 ,即 时,不等式 解为 .
综上可得, 当 时,不等式 解集为 ;
当 时,不等式 解集为 ;
当 时,不等式 解集为 .
19. 已知 是定义在 上的奇函数, .
(1)求函数 在 上的解析式;
(2)若 ,都有 成⽴,求实数 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据奇函数的性质 解得 ,并结合奇函数的定义检验;
第13⻚/共14⻚
学科⽹(北京)股份有限公司(2)根据题意分析可得 ,换元令 ,构造 ,结合函数单调性求最⼩值即可得
结果.
【⼩问1详解】
因为 是定义在 上的奇函数,则 ,解得 ,
可得 ,
且 ,
即 符合题意,所以 .
【⼩问2详解】
由(1)可知: ,则 ,
若 ,即 ,
即 ;
因为 , 在 内单调递减,可知 在 内单调递减,
则 ,可得 ,即 ,
令 ,则 ,
构造 ,可知 在 内单调递减,则 ,
可得 ,所以实数 的取值范围为 .
第14⻚/共14⻚
学科⽹(北京)股份有限公司