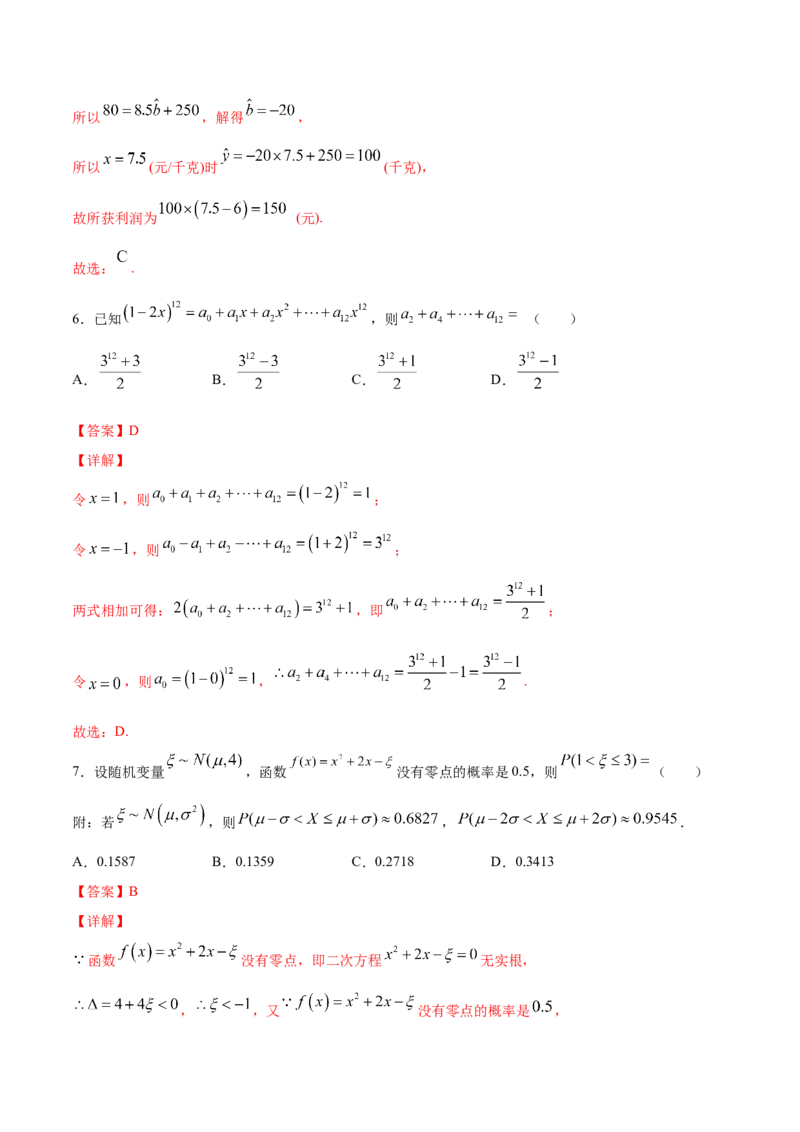文档内容
高二数学期末押题卷(一)
一、单项选择题(本大题共8题,每小题5分,共计40分。每小题列出的四个选项中只有一
项是最符合题目要求的)
1.设集合 , ,则 ( )
A. B. C. D.
【答案】B
【详解】
解: ,即 ,解得
即 ,因为 ,所以 .
故选:B
2.命题“ ,x2-2x+12 0”的否定为( )
A. , B. ,x2-2x+12 0
C. ,x2-2x+12 0 D. ,
【答案】A
【详解】
因为全称命题的否定是特称命题,
所以命题“ , ”的否定为 , .
故选:A.
3.校园歌手大赛共有 名同学成功进人决赛,其中 名男同学, 名女同学.现在他们站成一排合影留念,
要求 名男同学站在两端,则有( )种不同的站法.
A. B. C. D.
【答案】C
【详解】
先安排男生,方法有 ,再安排女生,方法有 ,所以不同的方法数有 .
故选:C
4.设随机变量 ,若 ,则 ( )
A.0.4 B.0.5 C.0.6 D.0.7
【答案】C
【详解】
随机变量 ,对称轴为:
因为 ,所以 ,
根据对称性可得 ,
则 .
故选:C.
5.2020年12月初某超市与蔬菜种植户签订进货合同,以 元/千克的单价购进一批大葱,并且每天都以不
同的价格投放市场,经过一个月的市场营销,得到该批大葱每天的销售量 (千克)与大葱的销售单价
(元/千克)的情况如下:
由表中数据计算出线性回归方程 中的 .若该超市将某一天大葱的销售价格定为 元/千
克时,则该超市这天销售大葱获得的利润估计为( )
A. B. C. D.
【答案】C
【详解】
因为 , ,所以 ,解得 ,
所以 (元/千克)时 (千克),
故所获利润为 (元).
故选: .
6.已知 ,则 ( )
A. B. C. D.
【答案】D
【详解】
令 ,则 ;
令 ,则 ;
两式相加可得: ,即 ;
令 ,则 , .
故选:D.
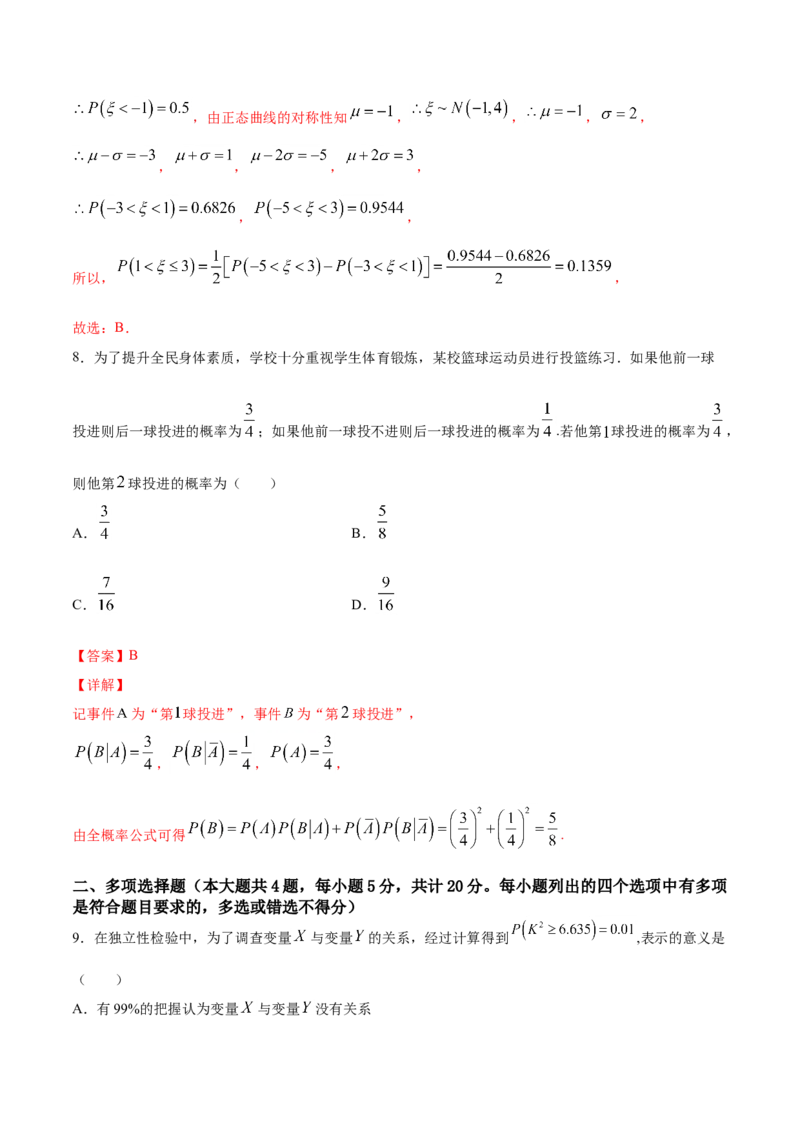
7.设随机变量 ,函数 没有零点的概率是0.5,则 ( )
附:若 ,则 , .
A.0.1587 B.0.1359 C.0.2718 D.0.3413
【答案】B
【详解】
函数 没有零点,即二次方程 无实根,
, ,又 没有零点的概率是 ,,由正态曲线的对称性知 , , , ,
, , , ,
, ,
所以, ,
故选:B.
8.为了提升全民身体素质,学校十分重视学生体育锻炼,某校篮球运动员进行投篮练习.如果他前一球
投进则后一球投进的概率为 ;如果他前一球投不进则后一球投进的概率为 .若他第 球投进的概率为 ,
则他第 球投进的概率为( )
A. B.
C. D.
【答案】B
【详解】
记事件 为“第 球投进”,事件 为“第 球投进”,
, , ,
由全概率公式可得 .
二、多项选择题(本大题共4题,每小题5分,共计20分。每小题列出的四个选项中有多项
是符合题目要求的,多选或错选不得分)
9.在独立性检验中,为了调查变量 与变量 的关系,经过计算得到 ,表示的意义是
( )
A.有99%的把握认为变量 与变量 没有关系B.有1%的把握认为变量 与变量 有关系
C.有99%的把握认为变量 与变量 有关系
D.有1%的把握认为变量 与变量 没有关系
【答案】CD
【详解】
在独立性检验中,由 .
表示的意义是:有1%的把握认为变量 与变量 没有关系,所以D正确.
即有99%的把握认为变量 与变量 有关系,所以C正确.
故选:CD
10.(多选)设X是一个离散型随机变量,则下列不能成为X的概率分布列的一组数据是( )
A.0, ,0,0, B.-0.2,0.2,-0.4,0.4
C.p,1-p(0≤p≤1) D. , ,…,
【答案】BD
【详解】
根据分布列的性质可知,所有的概率和等于1,且0≤P≤1.
对于A:因为0+ +0+0+ =1,且满足0≤P≤1,所以A选项能成为X的概率分布列的一组数据;
对于B:因为-0.2+0.2-0.4+0.4=0,且不满足0≤P≤1,所以B选项不能成为X的概率分布列的一组数据;
对于C:因为p+1-p=1,且满足0≤p≤1,故C选项能成为X的概率分布列的一组数据;
对于D:因为 + +…+ =1- = ,所以D选项不能作为随机变量的分布列的一组概率
取值,
故选:BD.
11.对于 关于下列排列组合数,结论正确的是( )
A. B.
C. D.
【答案】ABD【详解】
由题意,利用组合数的运算公式和性质,可得 , ,
所以A、B正确;
因为 , ,
所以C不正确;
由 ,
,所以D正确.
故选:ABD.
12.设随机变量 表示从1到 这 个整数中随机抽取的一个整数, 表示从1到 这 个整数中随机
抽取的一个整数,则( )
A.当 时,
B.当 时,
C.当 ( 且 )时,
D.当 时, 的数学期望为
【答案】BCD
【详解】
对A,当 时, , ,则 ,故A错误;
对B,当 时, ,则由 可得 或 ,,故B正确;
对C,当 ( 且 )时, , ,则 ,故C
正确;
对D,当 时, 的可能取值为1,2,则
,
,故 的数学期望为 ,故D正确.
三、填空题(每小题5分,共计20分)
13.将组成篮球队的10个名额分配给7个学校,每校至少1名,则名额的分配方式共有________种.
【答案】84
【详解】
解析:问题等价于将排成一行的10个相同元素分成7份的方法数,相当于在10个相同元素的9个间隔(除
去两端)中插入6块隔板隔成7份,共有 (种).所以名额分配方式有84种.
故答案为:84
14.已知随机变量 ,若 ,则 的值等于
__________.
【答案】
【详解】
,解得 ( 舍去),.
故答案为: .
15.在 的展开式中, 的系数为________.
【答案】
【详解】
因为 展开式的通项为 ,
所以 的系数为 .
故答案为: .
16.世卫组织就新型冠状病毒感染的肺炎疫情称,新型病毒可能造成“持续人传人”.通俗点说就是存在
A传B,B又传C,C又传D,这就是“持续人传人”.那么A、B、C就会被称为第一代、第二代、第三代
传播者.假设一个身体健康的人被第一代、第二代、第三代传播者感染的概率分别为0.9,0.8,0.7,健康
的小明参加了一次多人宴会,事后知道,参加宴会的人有5名第一代传播者,3名第二代传播者,2名第三
代传播者,试计算,小明参加聚会,仅和感染的10个人其中一个接触,感染的概率有多大________.
【答案】
【详解】
设事件 , , 为第一代、第二代、第三代传播者接触,
事件 为小明被感染,由已知得:
(A) , (B) , (C) , , , ,
(D) (A) (B) (C)
.小明参加聚会,仅和感染的10个人其中一个接触,感染的概率为0.83.
四、解答题(解答题需写出必要的解题过程或文字说明,17题10分,其余各题每题各12
分)
17.已知 展开式的二项式系数和为512,且
(1)求 的值;
(2)求 被6整除的余数.
【详解】
(1)因为 展开式的二项式系数和为 ,
所以 ,
故 .
令 ,可得 ,
令 ,可得 ,
即 ,
.
(2)
显然,展开式除了最后2项外,其余各项都能被6整除,
故展开式被6整出的余数,即 被6整除的余数为5.
18.两台车床加工同样的零件,第一台出现废品的概率是0.03,第二台出现废品的概率是0.02.加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍.
(1)求任意取出的零件是合格品的概率;
(2)如果任意取出的零件是废品,求它是第二台车床加工的概率.
【详解】
设A表示“第i台机床加工的零件”(i=1,2);B表示“出现废品”;C表示“出现合格品”.
i
(1)P(C)=P(AC∪AC)=P(AC)+P(AC)=P(A)P(C|A)+P(A)P(C|A)
1 2 1 2 1 1 2 2
= ×(1-0.03)+ ×(1-0.02)≈0.973.
(2)P(A|B)
2
19.为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n株沙柳,各
株沙柳成活与否是相互独立的,成活率为p.设ξ为成活沙柳的株数,数学期望E(ξ)=3,标准差 =
.
(1)求 的值并写出 的分布列;
(2)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率.
【详解】
由题意,每一株沙柳成活率均为 ,种植了n株沙柳,相当于n重伯努利试验,
所以随机变量ξ服从二项分布 ,且 ,
(1)由二项分布的期望和方差的公式,可得 ,
可得 ,解得 .
所以随机变量 的分布列为ξ 0 1 2 3 4 5 6
P
(2)记“需要补种沙柳”为事件 ,则 .
20.高中阶段有这样一句话,成也数学败也数学,意思是说数学成绩好的同学总成绩也好,数学成绩不好
的同学总成绩也不好.某市教育局对本届高三学生的上学期期末考试成绩进行随机调查得到如下 列联
表:
总成绩好 总成绩不好 总计
数学成绩好
数学成绩不好
总计
(1)求表中 的值;
(2)能否有 的把握认为学生总成绩不好与数学成绩不好有关?
附:
【详解】
(1)由 的列联表中的数据,可得 ,得 .
由 ,得 .
由 ,得 .
由 ,得 .(2)由独立性检验的公式,可得 ,
因此有 的把握认为学生总成绩不好与数学成绩不好有关.
21.某品牌汽车4S店对2020年该市前几个月的汽车成交量进行统计,用 表示2020年第 月份该店汽车
成交量,得到统计表格如下:
1 2 3 4 5 6 7 8
14 12 20 20 22 24 30 26
(1)求出 关于 的线性回归方程 ,并预测该店9月份的成交量;( , 精确到整数)
(2)该店为增加业绩,决定针对汽车成交客户开展抽奖活动,若抽中“一等奖”获5千元奖金;抽中“二
等奖”获2千元奖金;抽中“祝您平安”则没有奖金.已知一次抽奖活动中获得“二等奖”的概率为 ,
没有获得奖金的概率为 .现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所
获奖金总额 (千元)的分布列及数学期望.
参考数据及公式: , , , .
【详解】
(1)由题意得: , ,
∴ ,∴
所以,回归直线方程为 ,∴当 时, ,即预计9月份的成交量为30辆;
(2)由题意得:获得“一等奖”的概率为 ,
所以 的可能取值为0,2,4,5,7,10,
∴ , ,
, ,
, ,
所以 的分布列为:
0 2 4 5 7 10
∴ .
22.已知函数 .
(1)证明:函数 在区间 内存在零点;
(2)设函数 ,若 在 上单调递增,求实数 的取值范围.
【详解】
(1)由题得, ,
由零点存在定理可知, 在区间 内存在零点(2) 在 上单调递增,
对 恒成立,
令 ,
则 ,
当 时, ;
当 时, ;
函数 在区间 上单调递减,在区间 上单调递增,
实数 的取值范围为