文档内容
2024-2025 学年广东省佛山市 H7 联盟高一下学期 5 月联考
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知四棱锥有m条棱,n个顶点,则m−n=( )
A. 2 B. 3 C. 4 D. 5
2.若向量⃗
a=(−3,x)
,⃗
b=(7,y)
,且
⃗a⊥⃗b
,则
A. 7x+3 y=0 B. 7x−3 y=0 C. xy=21 D. xy=−21
2 a 5
3.已知△ABC的内角A,B,C的对边分别为a,b,c,且sinB= , = ,则sinA=
3 b 6
5 4 3 2
A. B. C. D.
9 9 5 5
4.方程x2−x+4=0的复数根为( )
1 √15 1 √15
A. ± i B. − ± i C. 1±√15i D. −1±√15i
2 2 2 2
5.已知点A(−1,−1),B(2,−2),C(0,1),则向量⃗AB在向量⃗AC方向上的投影向量的坐标为( )
A. (√5 2√5) B. C. (1 2) D.
, (√5,2√5) , (1,2)
5 5 5 5
6.已知 为第二象限角,且 √26,则 ( π)
α sinα= tan α+ =
26 4
3 3 2 2
A. − B. C. − D.
2 2 3 3
第 页,共 页
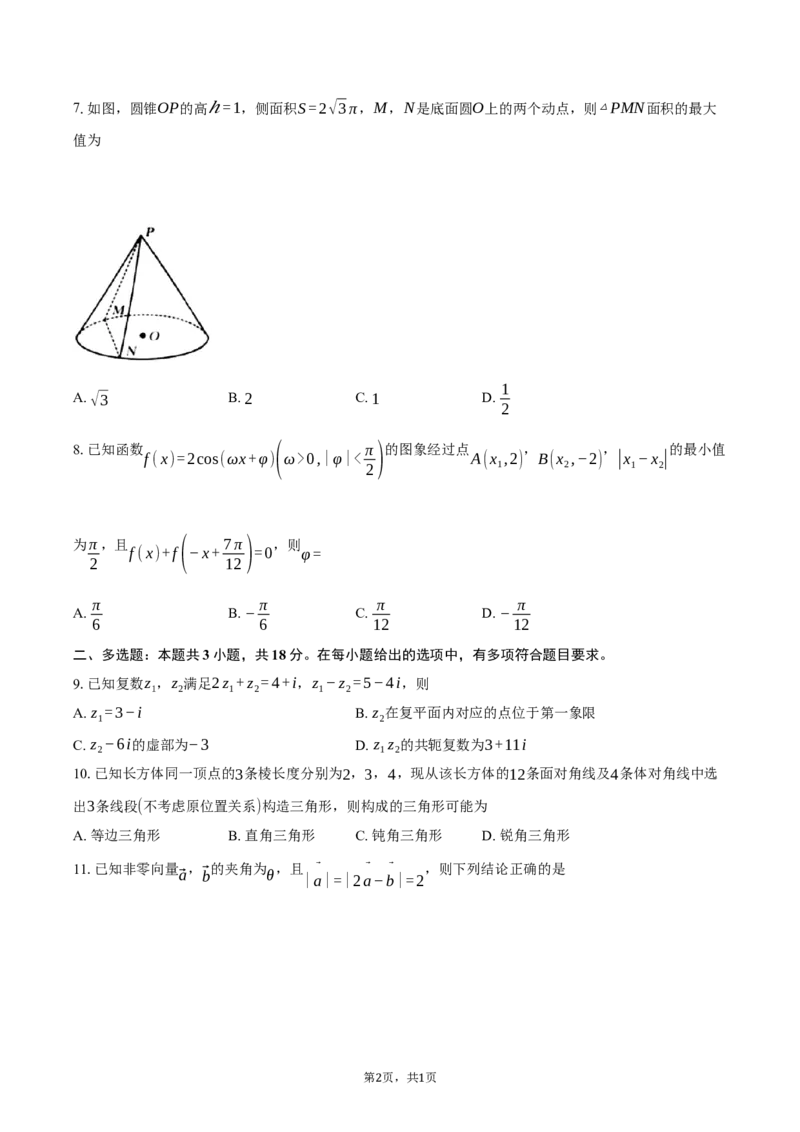
1 17.如图,圆锥OP的高ℎ =1,侧面积S=2√3π,M,N是底面圆O上的两个动点,则△PMN面积的最大
值为
1
A. √3 B. 2 C. 1 D.
2
8.已知函数 ( π)的图象经过点 , , 的最小值
f(x)=2cos(ωx+φ) ω>0,|φ|< A(x ,2) B(x ,−2) |x −x |
2 1 2 1 2
为π,且 ( 7π) ,则
f(x)+f −x+ =0 φ=
2 12
π π π π
A. B. − C. D. −
6 6 12 12
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知复数z ,z 满足2z +z =4+i,z −z =5−4i,则
1 2 1 2 1 2
A. z =3−i B. z 在复平面内对应的点位于第一象限
1 2
C. z −6i的虚部为−3 D. z z 的共轭复数为3+11i
2 1 2
10.已知长方体同一顶点的3条棱长度分别为2,3,4,现从该长方体的12条面对角线及4条体对角线中选
出3条线段(不考虑原位置关系)构造三角形,则构成的三角形可能为
A. 等边三角形 B. 直角三角形 C. 钝角三角形 D. 锐角三角形
11.已知非零向量 , 的夹角为 ,且 ⃗ ⃗ ⃗ ,则下列结论正确的是
⃗a ⃗b θ
|a|=|2a−b|=2
第 页,共 页
2 17
A. 若
|
⃗
b|=3
,则cosθ= B. 若⃗a//⃗b,则
|
⃗
b|=2
8
C. 的取值范围为[ π] D. 的最大值为
θ 0, ⃗a⋅⃗b 12
6
三、填空题:本题共3小题,每小题5分,共15分。
12.| 6 | __________.
=
√5−i
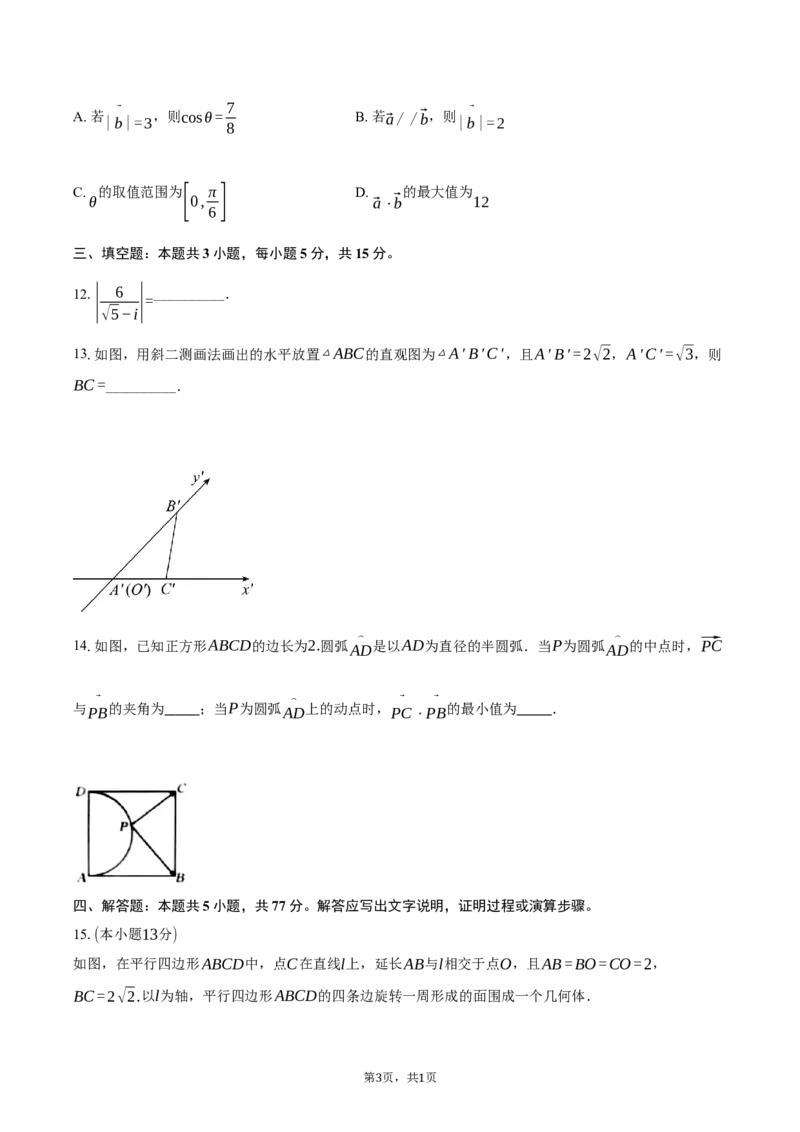
13.如图,用斜二测画法画出的水平放置△ABC的直观图为△A′B′C′,且A′B′=2√2,A′C′=√3,则
BC=__________.
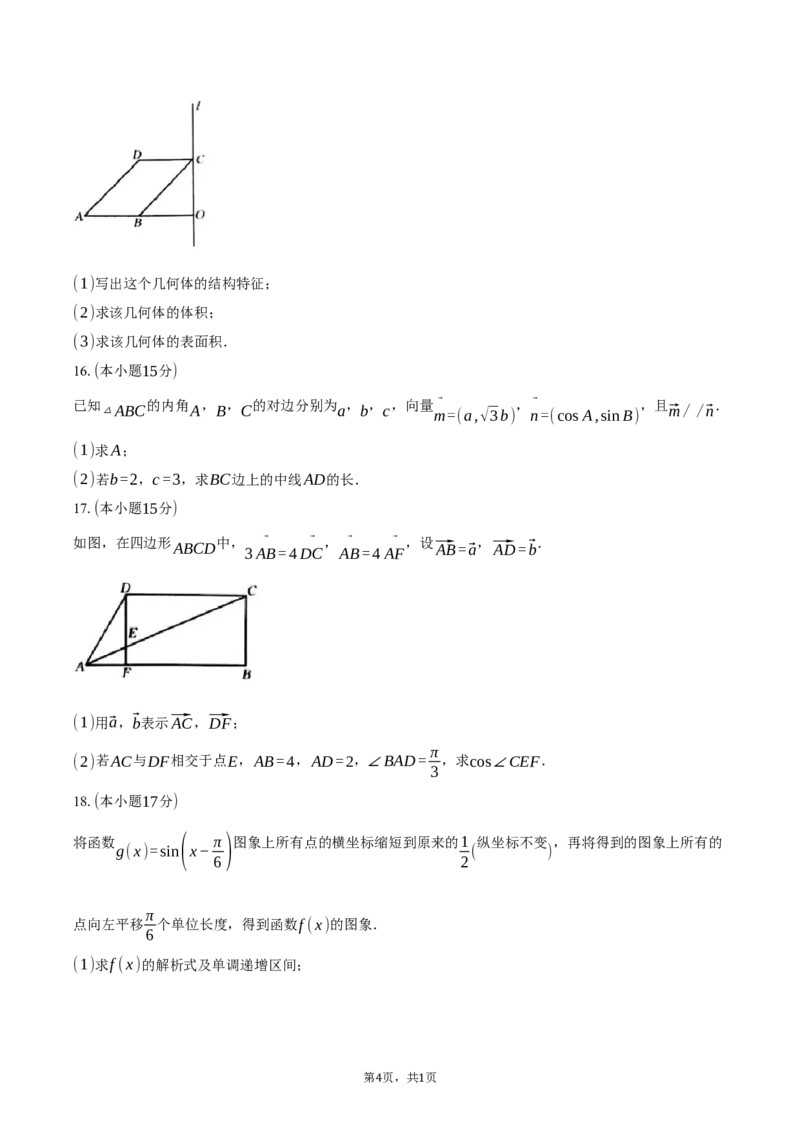
14.如图,已知正方形ABCD的边长为2.圆弧 ⌢ 是以AD为直径的半圆弧.当P为圆弧 ⌢ 的中点时,⃗PC
AD AD
与 ⃗ 的夹角为 ;当P为圆弧 ⌢ 上的动点时, ⃗ ⃗ 的最小值为 .
PB AD PC⋅PB
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
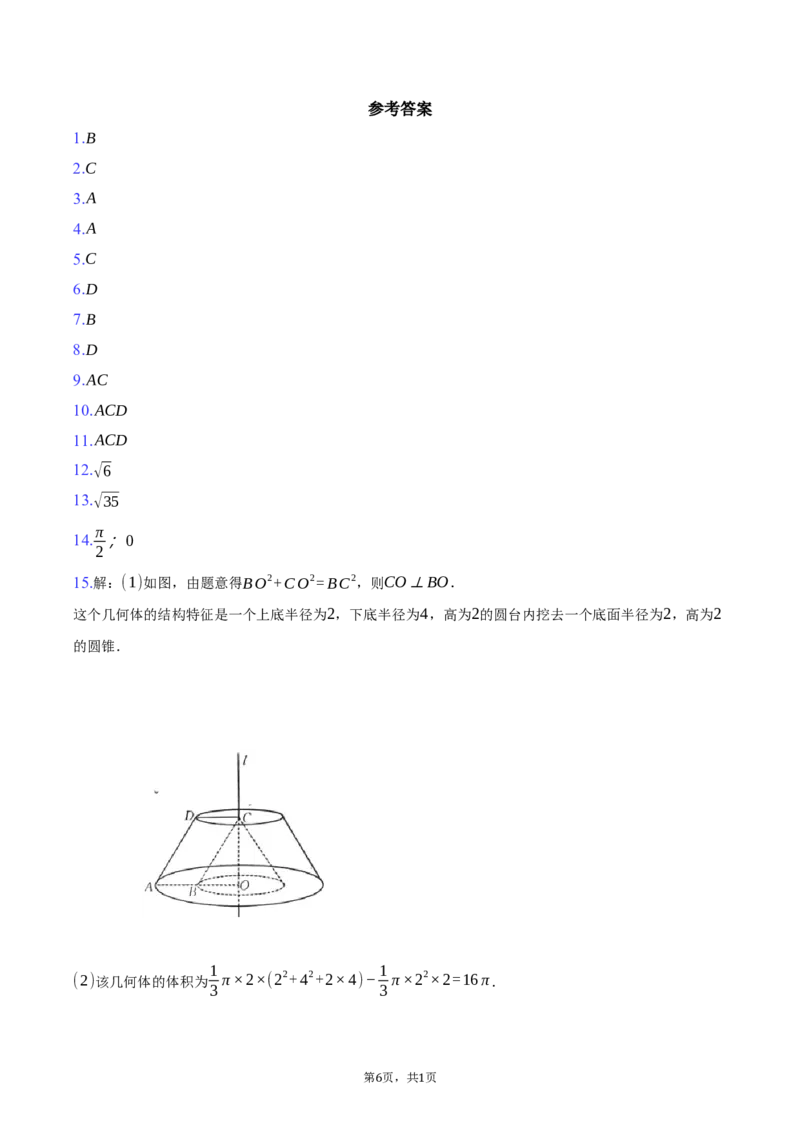
15.(本小题13分)
如图,在平行四边形ABCD中,点C在直线l上,延长AB与l相交于点O,且AB=BO=CO=2,
BC=2√2.以l为轴,平行四边形ABCD的四条边旋转一周形成的面围成一个几何体.
第 页,共 页
3 1(1)写出这个几何体的结构特征;
(2)求该几何体的体积;
(3)求该几何体的表面积.
16.(本小题15分)
已知 △ABC 的内角 A , B , C 的对边分别为 a , b , c ,向量 m ⃗ =(a,√3b) ,⃗ n=(cosA,sinB) ,且 ⃗m//⃗n .
(1)求A;
(2)若b=2,c=3,求BC边上的中线AD的长.
17.(本小题15分)
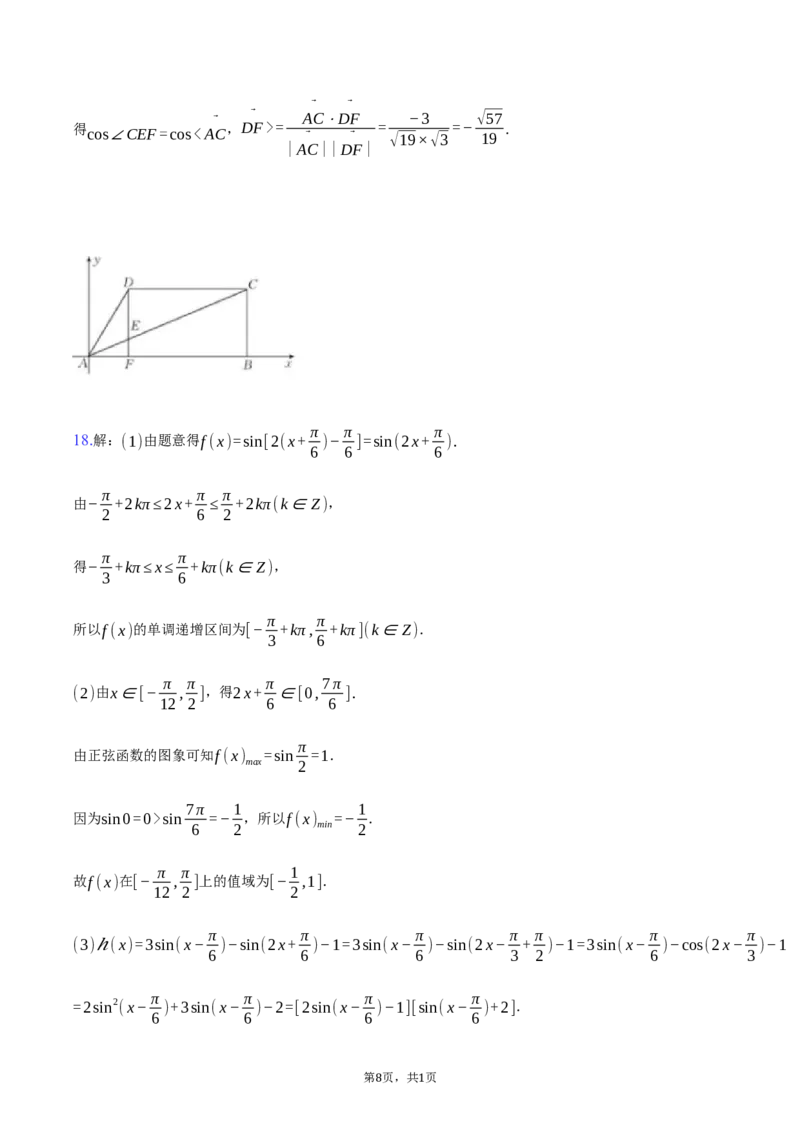
如图,在四边形 中, ⃗ ⃗ , ⃗ ⃗ ,设 , .
ABCD
3AB=4DC AB=4AF
⃗AB=⃗a ⃗AD=⃗b
(1)用⃗a,⃗b表示⃗AC,⃗DF;
π
(2)若AC与DF相交于点E,AB=4,AD=2,∠BAD= ,求cos∠CEF.
3
18.(本小题17分)
将函数 ( π)图象上所有点的横坐标缩短到原来的1 纵坐标不变 ,再将得到的图象上所有的
g(x)=sin x− ( )
6 2
π
点向左平移 个单位长度,得到函数f(x)的图象.
6
(1)求f(x)的解析式及单调递增区间;
第 页,共 页
4 1求 在[ π π]上的值域;
(2) f(x) − ,
12 2
(3)求函数ℎ(x)=3g(x)−f(x)−1在[0,4π]上的零点之和.
19.(本小题17分)
已知△ABC的内角A,B,C的对边分别为a,b,c,且5sin2B+5sin2C=6sinBsinC+5sin2A.
(1)求cosA;
(2)若a=2√5,求△ABC面积的最大值;
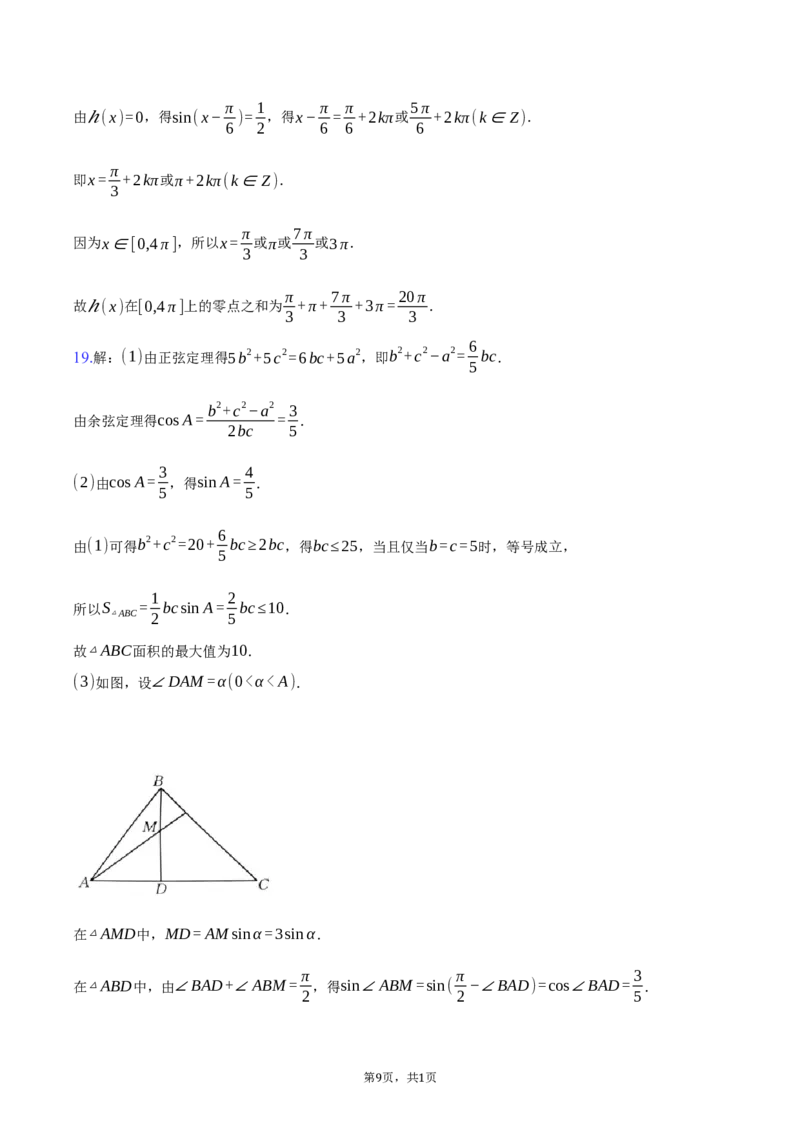
(3)若△ABC的垂心为M(M在△ABC的内部),直线BM与AC交于点D,且AM=3,当AB+MD最大时,
求AB.
第 页,共 页
5 1参考答案
1.B
2.C
3.A
4.A
5.C
6.D
7.B
8.D
9.AC
10.ACD
11.ACD
12.√6
13.√35
π
14. ;0
2
15.解:(1)如图,由题意得BO2+CO2=BC2,则CO⊥BO.
这个几何体的结构特征是一个上底半径为2,下底半径为4,高为2的圆台内挖去一个底面半径为2,高为2
的圆锥.
1 1
(2)该几何体的体积为 π×2×(22+42+2×4)− π×22×2=16π.
3 3
第 页,共 页
6 1(3)由题意得AD=BC=2√2.,
则该几何体的表面积为π×(22+2×2√2+4×2√2)+π×(42−22 )+π×2×2√2=(16+16√2)π.
16.解:(1)由题意得asinB=√3bcosA.
由正弦定理得sin AsinB=√3sinBcosA.
因为B∈(0,π),所以sinB≠0,则sin A=√3cosA,
π
得tan A=√3,得A= ;
3
⃗ 1 ⃗ 1 ⃗
(2)由题意得AD= AB+ AC,则
2A
⃗
D=A
⃗
B+A
⃗
C
,
2 2
两边平方得 ⃗ ⃗ ⃗ ⃗ ⃗ ,
4 AD2=AB2+2AB⋅AC+AC2
1
得4AD2=b2+c2+2bccos∠BAC=4+9+2×2×3× =19,
2
√19
得AD= ,
2
√19
所以BC边上的中线AD的长为 .
2
⃗ ⃗ ⃗ ⃗ 3 ⃗ 3
17.解:(1)由题意得AC=AD+DC=AD+ AB= ⃗a+⃗b,
4 4
⃗ ⃗ ⃗ 1 ⃗ ⃗ 1
DF=AF−AD= AB−AD= ⃗a−⃗b.
4 4
(2)如图,以A为原点,AB所在直线为x轴,过点A所作AB的垂线为y轴,建立平面直角坐标系.
A(0,0),D(1,√3),C(4,√3),F(1,0)
⃗ ⃗
则AC=(4,√3) ,DF=(0,−√3) ,
第 页,共 页
7 1⃗ ⃗
得 cos∠CEF=cos=
⃗
AC⋅D
⃗
F
=
√19
−
×
3
√3
=−
√
1
5
9
7
.
|AC||DF|
π π π
18.解:(1)由题意得f(x)=sin[2(x+ )− ]=sin(2x+ ).
6 6 6
π π π
由− +2kπ≤2x+ ≤ +2kπ(k∈Z),
2 6 2
π π
得− +kπ≤x≤ +kπ(k∈Z),
3 6
π π
所以f(x)的单调递增区间为[− +kπ, +kπ](k∈Z).
3 6
π π π 7π
(2)由x∈[− , ],得2x+ ∈[0, ].
12 2 6 6
π
由正弦函数的图象可知f(x) =sin =1.
max 2
7π 1 1
因为sin0=0>sin =− ,所以f(x) =− .
6 2 min 2
π π 1
故f(x)在[− , ]上的值域为[− ,1].
12 2 2
π π π π π π π
(3)ℎ(x)=3sin(x− )−sin(2x+ )−1=3sin(x− )−sin(2x− + )−1=3sin(x− )−cos(2x− )−1
6 6 6 3 2 6 3
π π π π
=2sin2 (x− )+3sin(x− )−2=[2sin(x− )−1][sin(x− )+2].
6 6 6 6
第 页,共 页
8 1π 1 π π 5π
由ℎ(x)=0,得sin(x− )= ,得x− = +2kπ或 +2kπ(k∈Z).
6 2 6 6 6
π
即x= +2kπ或π+2kπ(k∈Z).
3
π 7π
因为x∈[0,4π],所以x= 或π或 或3π.
3 3
π 7π 20π
故ℎ(x)在[0,4π]上的零点之和为 +π+ +3π= .
3 3 3
6
19.解:(1)由正弦定理得5b2+5c2=6bc+5a2,即b2+c2−a2= bc.
5
b2+c2−a2 3
由余弦定理得cosA= = .
2bc 5
3 4
(2)由cosA= ,得sin A= .
5 5
6
由(1)可得b2+c2=20+ bc≥2bc,得bc≤25,当且仅当b=c=5时,等号成立,
5
1 2
所以S = bcsin A= bc≤10.
△ABC 2 5
故△ABC面积的最大值为10.
(3)如图,设∠DAM=α(0<α