文档内容
选择性必修第二册 期末模块检测试卷 基础A卷
解析版
学校:___________姓名:___________班级:___________考号:___________
题型:8(单选)+4(多选)+4(填空)+6(解答),满分150分,时间:120分钟
一、单选题
1.已知等比数列 中, , ,则 ( )
A. B. C. D.
【答案】A
【分析】
根据题意,将条件表示为 的形式,计算出 ,再计算 即可.
【详解】
∵等比数列 中, , ,
∴ ,解得 ,
∴ .
故选:A.
2.已知等差数列 的前n项和为 , =5,则 =( )
A.5 B.25 C.35 D.50
【答案】B
【分析】
根据等差中项及等差数列求和公式即可求解.
【详解】
由题意可知, 为等差数列,所以
故选:B
3.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日五尺,问日织几何?”意
思是:“女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这名女子每天分
别织布多少?”某数学兴趣小组依托某制造厂用织布机完全模拟上述情景,则从第一天开始,要使织
布机织布的总尺数为165尺,则所需的天数为( )
A.7 B.8 C.9 D.10
【答案】D
【分析】
设该女子第一天织布 尺,根据题意,求得 尺,结合等比数列的求和公式,列出方程,即
可求解.
【详解】
设该女子第一天织布 尺,则5天共织布 ,解得 尺,在情境模拟下,设需要
天织布总尺数达到165尺,则有 整理得 ,解得 .故选:D.
4.观察下列式子: , , ,…,则可归纳出
小于( )
A. B. C. D.
【答案】C
【分析】
根据已知式子分子和分母的规律归纳出结论.
【详解】
由已知式子可知所猜测分式的分母为 ,分子第 个正奇数,即 ,.
故选:C.
5.设曲线 在点 处的切线方程为 ,则 ( )
A.0 B.1 C.2 D.3
【答案】D
【分析】
利用 可求得答案.
【详解】
,∵ ,则 .
故选:D
6.已知数列 , 都是等差数列,记 , 分别为 , 的前n项和,且
,则 =( )
A. B. C. D.
【答案】D
【分析】
利用等差数列的性质以及前 项和公式即可求解.
【详解】
由 ,
.
故选:D
7.已知函数 ,其导函数为 ,则的值为( )
A.1 B.2 C.3 D.4
【答案】C
【分析】
求得可得 的解析式,求出 解析式,可得 为偶函数,即可求出
的值,再求 ,即可求得 的值,
即可求得答案.
【详解】
, ,
所以 为偶函数,所以 ,
因为 ,
所以 ,
所以 .
故选:C.
8.已知函数 有两个零点,则实数 的取值范围是( )
A. B. C. D.
【答案】B
【分析】
分离变量,利用导函数应用得到函数在 无零点,则 有两个零点,利用函数最值得到参
数范围
【详解】
当 时, ,∴ 不是函数 的零点.当 时,由 ,得,设 , ,则 在 上单调递减,且
.所以 时无零点
当 时, 等价于 ,令 , ,
得 在 上单调递减,在 上单调递增, , .
因为 有2个零点,所以 .
故选:B.
【点睛】
分离变量法,利用导数求函数的单调性,极值是解题关键.
二、多选题
9.已知递减的等差数列 的前 项和为 , ,则( )
A. B. 最大
C. D.
【答案】ABD
【分析】
转化条件为 ,进而可得 , ,再结合等差数列的性质及前n项和公式逐项判
断即可得解.
【详解】
因为 ,所以 ,即 ,
因为数列 递减,所以 ,则 , ,故A正确;
所以 最大,故B正确;
所以 ,故C错误;所以 ,故D正确.
故选:ABD.
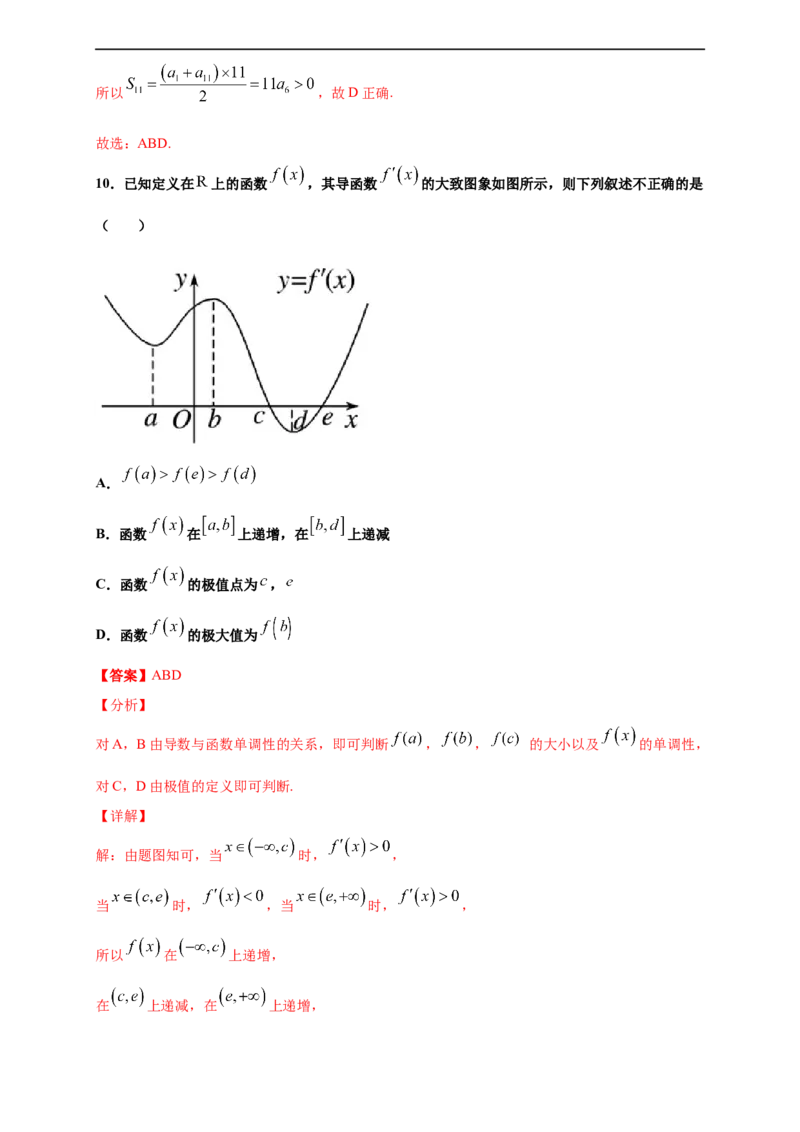
10.已知定义在 上的函数 ,其导函数 的大致图象如图所示,则下列叙述不正确的是
( )
A.
B.函数 在 上递增,在 上递减
C.函数 的极值点为 ,
D.函数 的极大值为
【答案】ABD
【分析】
对A,B由导数与函数单调性的关系,即可判断 , , 的大小以及 的单调性,
对C,D由极值的定义即可判断.
【详解】
解:由题图知可,当 时, ,
当 时, ,当 时, ,
所以 在 上递增,
在 上递减,在 上递增,对A, ,故A错误;
对B,函数 )在 上递增,在 上递增,在 上递减,故B错误;
对C,函数 的极值点为 , ,故C正确;
对D,函数 的极大值为 ,故D错误.
故选:ABD.
11.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一
半,如此六日过其关”.则下列说法正确的是( )
A.此人第六天只走了5里路
B.此人第一天走的路程比后五天走的路程多6里
C.此人第二天走的路程比全程的 还多1.5里
D.此人走的前三天路程之和是后三天路程之和的8倍
【答案】BCD
【分析】
设此人第 天走 里路,则 是首项为 ,公比为 的等比数列,由 求出 ,然后求
出相应的项,判断各选项.
【详解】
解:根据题意此人每天行走的路程成等比数列,
设此人第 天走 里路,则 是首项为 ,公比为 的等比数列.
所以 ,解得 .
选项A: ,故A错误,
选项B:由 ,则 ,又 ,故B正确.选项C: ,而 , ,故C正确.
选项D: ,
则后3天走的路程为 ,
而且 ,D正确.
故选:BCD.
【点睛】
关键点点睛:本题考查等比数列的应用,解题关键是引入等比数列 , 表示第 天行走的路
程,根据前6项的和求出首项 ,然后可得通项公式,从而判断出结论.
12.已知数列 的前 项和为 ,则下列说法正确的是( )
A. B. 为 的最小值
C. D.
【答案】AC
【分析】
利用和与项的关系,分 和 分别求得数列的通项公式,检验合并即可判定A;
根据数列的项的正负情况可以否定B;根据前16项都是正值可计算判定C;注意到
可计算后否定D.
【详解】
,
,
对于 也成立,
所以 ,故A正确;当 时, ,当n=17时 ,当 时, ,
只有最大值,没有最小值,故B错误;
因为当 时, ,∴ ,故C正确;
,
故D错误.
故选:AC.
【点睛】
本题考查数列的和与项的关系,数列的和的最值性质,绝对值数列的求和问题,属小综合题.
和与项的关系 ,若数列 的前 项为正值,往后都是小于等于零,则当
时有 ,若数列 的前 项为负值,往后都是大于或等于零,
则当 时有 .若数列的前面一些项是非负,后面的项为负值,则
前 项和只有最大值,没有最小值,若数列的前面一些项是非正,后面的项为正值,则前 项和只
有最小值,没有最大值.
三、填空题
13.已知 ,则 等于__________.(用数字作答)
【答案】-2
【分析】
求出 的导函数,代入 即可求解.
【详解】
,,
,解得 .
故答案为: .
14. 对任意 都有 .数列 满足:
,则 __________.
【答案】
【分析】
采用倒序相加法即可求得结果.
【详解】
由题意得: , , ,……,
,
,
,解得: .
故答案为: .
【点睛】
本题考查利用倒序相加法求和的问题,属于基础题.
15.已知 ,对任意的 都有 ,则 的取值范围为_______.
【答案】
【分析】利用导数研究函数的单调性,进而求得在给定区间上的最大值,根据不等式恒成立的意义即得实数
a的取值范围.
【详解】
由 得 或 ,
在区间[-2,0)上 , 单调递增;在(0,2)内时 单调递减.
又 , , ,
∴ ,
又 对于任意的x∈[-2,2]恒成立,
∴ ,即a的取值范围是
故答案为: .
【点睛】
本题考查利用导数研究函数的在闭区间上的最值进而求不等式恒成立中的参数范围,属基础题,关
键在于利用导数研究函数的单调性,求得在给定区间上的最大值.
16.古代埃及数学中有一个独特现象:除 用一个单独的符号表示以外,其他分数都可写成若干个
单分数和的形式.例如 ,可这样理解:假定有两个面包,要平均分给5个人,如果每人
,不够,每人 ,余 ,再将这 分2成5份,每人得 ,这样每人分得 .形如
的分数的分解: , , ,按此规律,则
________ .【答案】
【分析】
根据 , , ,
…进行归纳推理.
【详解】
由题意得, ,即 ,
,即 ,
,即 ,
由此归纳出 .
经验证 ,结论成立,
∴ .
故答案为: .
【点睛】
方法点睛:由数列的前 项归纳通项公式时,首先要分析项的结构,然后再探究结构中的各部分与
项的序号 间的函数关系,进而求得通项公式.
四、解答题
17.已知数列 各项均为正数,其前 项和为 ,且满足 .
(1)求数列 的通项公式.(2)设 ,求数列 的前 项和 .
【答案】(1) ;(2) .
【分析】
(1)由 可得 ,再由 时, 与条件作差可得 ,从而利
用等差数列求通项公式即可;
(2)由 利用裂项相消求和即可.
【详解】
(1)∵ ,
∴ ,解得 ,
当 时,由 ①可得,
②,
①-②: ,
∵ ,∴ ,∴ ,
即∴ ,
∴ 是以 为首项,以 为公差的等差数列,
∴
综上所述,结论是: .
(2)由(1)可得
∴,
综上所述, .
18.在① ,② ,③ 这三个条件中任选两个,补充在下面的问题
中.若问题中的 存在,求出 的值;若不存在,请说明理由.
设等差数列 的前 项和为 , 是各项均为正数的等比数列,设前 项和为 ,若
, ,且 .是否存在大于 的正整数 ,使得 成等比数列?
(注:如果选择多个条件分别解答,按第一个解答计分.)
【答案】答案见解析.
【分析】
由等比数列的条件,求得 ,可得等比数列的通项公式.然后分别选取条件①②,条件①③,
条件②③,列出关于等差数列首项与公差的方程组,求得首项与公差,得到等差数列的通项公式及
前 项和,再由 , , 成等比数列列式求解 值即可.
【详解】
解:设 的 公差为 , 的公比为 ,
由题意知 ,所以 ,
整理得 ,因为 ,所以 ,所以 .
(1)当选取的条件为①②时,有 ,所以 ,
解得 .
所以 .
所以 ,若 成等比数列,则 ,
所以 ,解得 ,
因为 为正整数,所以不符合题意,此时 不存在.
(2)当选取的条件为①③时,有 ,所以 ,
解得 .
所以 .
所以 ,
若 成等比数列,则 ,
所以 ,解得 或 (舍去)
此时存在正整数 满足题意.
(3)当选取的条件为②③时,有 ,所以 ,
解得 .
所以 .
所以 ,
若 成等比数列,则 ,即 ,
所以 ,解得 ,
因为 为正整数,所以不符合题意,此时 不存在.
【点睛】等比数列基本量的求解是等比数列中的一类基本问题,解决这类问题的关键在于熟练掌握等比数列
的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前n项和公式时,应该要分类讨
论,有时还应善于运用整体代换思想简化运算过程.
19.已知数列 中, ,
(1)证明:数列 是等比数列
(2)若数列 满足 ,求数列 的前 项和 .
【答案】(1)证明见解析 ;(2) .
【分析】
(1)由 可得 ,然后可得答案;
(2)由(1)可算出 , ,然后用错位相减法可算出答案.
【详解】
(1)证明:由 ,知
又 ,∴ 是以 为首项,3为公比的等比数列
(2)解:由(1)知 ,∴ ,
两式相减得∴
20.已知函数
(1)求函数 的单调区间;
(2)若方程 =0有两个不相等的实数根,求实数 的取值范围.
【答案】(1) 的单调递增区间是 ,单调递减区间是 .(2)
【分析】
(1)首先求出函数的导函数,再解不等式即可得到函数的单调区间;
(2)由 得 , 将此方程的根看作函数 与 的图象交点的横坐
标,结合(1)中相关性质得到函数的图象,数形结合即可得到参数的取值范围;
【详解】
解:(1)∵
所以
∴当 时, ,当 时, ;
即 的单调递增区间是 ,单调递减区间是 .
(2)由 得 ,
将此方程的根看作函数 与 的图象交点的横坐标,
由(1)知函数 在 时有极大值 ,作出其大致图象,∴实数 的取值范围是 .
【点睛】
本题考查利用导数研究函数的单调性及函数的零点问题,属于基础题.
21.设函数 , .
(1) 时,求 的最小值.
(2)若 在 恒成立,求 的取值范围.
【答案】(1)0;(2) .
【分析】
(1)当 时,求导可得 ,令 ,解得 ,分别讨论 和
时, 的正负,即可得 的单调性,即可求得答案;
(2)求导可得 ,设 ,分别讨论 和 时
的正负,可得 的单调性,进而可得 的单调性,综合分析,即可得答案.
【详解】
(1)当 时, ,则 ,
令 ,解得 ,
当 时, ,所以 在 单调递减函数;当 时, ,所以 在 单调递增函数;
所以 .
(2) ,则 ,
设 ,则 ,
当 时, ,所以 在 上为增函数,
又 ,所以 ,即 ,
所以 在在 上为增函数,又 ,
所以 ,满足题意;
当 时,令 ,解得 ,
当 时, ,所以 在 为减函数,
所以当 时, ,即 ,
所以 在 为减函数,又
所以 ,不满足题意,
综上:a的取值范围是【点睛】
解题的关键是熟练掌握利用导数求解函数单调性,极(最)值的方法,若处理恒成立问题时,需满
足 ,若处理存在性问题时,需满足 ,需仔细审题,进行求解,属中档题.
22.已知 .
(1)若函数 在 处取得极值,求实数 的值;
(2)若 ,求函数 的单调递增区间;
(3)若 ,存在正实数 ,使得 成立,求 的取值范围.
【答案】(1) ;(2)答案见解析;(3) .
【分析】
(1)由题意结合极值的概念可得 ,解得 后,验证即可得解;
(2)求导得 ,按照 、 、 、 分类讨论,求
得 的解集即可得解;
(3)转化条件得 ,令 ,
,求导确定 的单调性和值域即可得解.
【详解】
(1) ,
∵函数 在 处取得极值, ,解得 ,
当 时, .∴当 时, , 单调递减;
当 时, , 单调递增;
∴当 时,函数 在 处取得极小值;
(2) ,
,
令 ,则 或 ,
①当 时,令 可得 ,
∴函数 的单调递增区间为 ;
②当 时,令 可得 或 ,
∴函数 的单调递增区间为 ;
③当 时, 在 上恒成立,
∴函数 的单调递增区间为 ;
④当 时,令 可得 或 ,
∴函数 的单调递增区间为 ;
(3) , ,
, ,
整理可得 ,令 , ,
,令 ,解得 ,
当 时, , 单调递减;当 时, , 单调递增;
∴当 时, 取得极小值即最小值为 ,
即 ,
解得 (舍去)或 ,
的取值范围为 .
【点睛】
本题考查了导数的综合应用,考查了运算求解能力、逻辑推理能力、分类讨论思想,属于中档题.