文档内容
期末模拟卷
(B 能力卷)
班级______ 姓名_______ 考号______
一、单项选择题(本大题共8题,每小题5分,共计40分。每小题列出的四个
选项中只有一项是最符合题目要求的)
1.已知 ,则 ( )
A.2 B. C. D.1
【答案】D
【详解】
由题意得 ,
所以 ,则 .
故选:D
2.已知 , , ,则 ( )
A. B. C. D.
【答案】B
【详解】
由于 ,
所以 ,
所以 .
所以 ,
由于向量的夹角的取值范围是 ,
所以 的夹角为 .
故选:B
3.已知 是直角三角形 内的一点,直角三角形 斜边 长为4,若点 在 上,
满足 ,则 等于( )
A.4 B.2 C.1 D.【答案】B
【详解】
由 可得 ,即 ,取 中
点 ,
易得 ,则 , 和 重合,则 .
故选:B.
4.已知m,n是两条不同的直线,α,β是两个不同的平面,则( )
A.若m∥α,n∥α,则m∥n B.若m∥α,m⊥n,则n⊥α
C.若α∥β,m⊥α,n∥β,则m⊥n D.若m∥n,n α,则m∥α
【答案】C
⊂
【详解】
对于A,若m∥α,n∥α,则m∥n或m与n相交或m与n异面,故A错误;
对于B,若m∥α,m⊥n,则n∥α或n α或n与α相交,相交也不一定垂直,故B错误;
对于C,若α∥β,m⊥α,则m⊥β,又n∥β,∴m⊥n,故C正确;
⊂
对于D,若m∥n,n α,则m∥α或m α,故D错误.
故选:C.
⊂ ⊂
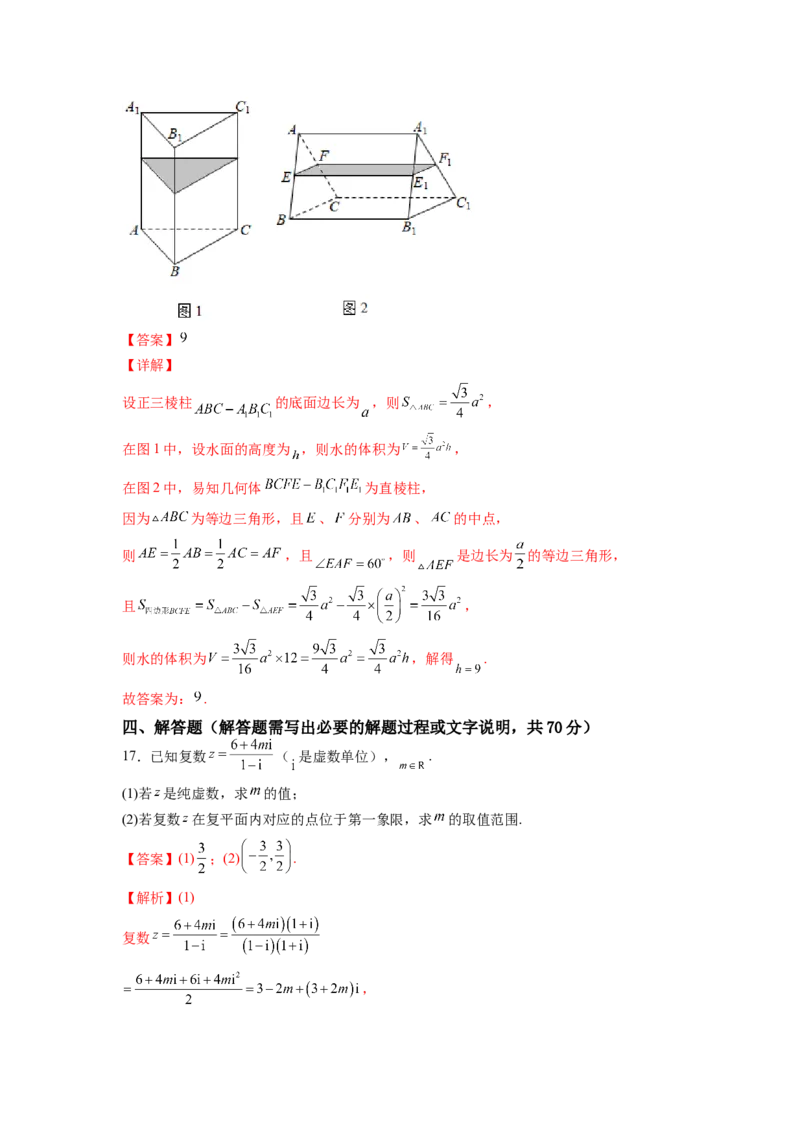
5.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤
维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图
所示.估计棉花纤维的长度的样本数据的80%分位数是( )
A.28 mm B.28.5 mm
C.29 mm D.29.5 mm
【答案】C
【详解】
棉花纤维的长度在25 mm以下的比例为 ,在30 mm以下的比例为 ,因此,80%分位数一定位于 内,
因 ,所以估计棉花纤维的长度的样本数据的80%分位数是29 mm.
故选:C
6.第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,是由中国举办的国际性奥
林匹克赛事,于2022年2月4日开幕,2月20日闭幕.小林观看了本届冬奥会后,打算从
冰壶、短道速滑、花样滑冰、冬季两项这四个项目中任意选两项进行系统的学习,则小林没
有选择冰壶的概率为( )
A. B. C. D.
【答案】C
【详解】
记冰壶、短道速滑、花样滑冰、冬季两项分别为A,B,C,D,则这四个项目中任意选两项的情况
有:AB,AC,AD,BC,BD,CD,6种情况,
其中没有选择冰壶的有:BC,BD,CD,3种情况,
所以所求概率为 .
故选:C
7.已知直三棱柱 的顶点都在一个球的球面上,若
,则该球的表面积为( )
A. B. C. D.
【答案】A
【详解】
设上下底面三角形外接圆的圆心为 ,则球心 在 的中点处,如图,设球的半径为 ,底面三角形外接圆的半径为 ,
则由正弦定理可知 ,即 ,
因为 ,所以 ,
所以 ,
故选:A
8.秦九韶是我国南宋著名数学家,在他的著作《数书九章》中有已知三边求三角形面积
的方法:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上以小斜幂乘大斜幂减上,余四
约之,为实一为从阳,开平方得积.”如果把以上这段文字写成公式就是
,其中a,b,c是 的内角A,B,C的对边,若
,且 ,则 面积S的最大值为( )
A. B. C. D.
【答案】B
【详解】
由 得 ,得 ,
所以,当且仅当 , 时,等号成立.
故选:B
二、多项选择题(本大题共4题,每小题5分,共计20分。每小题列出的四个
选项中有多项是符合题目要求的,多选或错选不得分)
9.若复数 (i为虚数单位),其中真命题为( )
A.若 ,则 B.若 ,则z为纯虚数
C.若 ,则 D.若 ,则
【答案】AC
【详解】
A: ,则 ,真命题;
B:若 ,则 ,此时 ,但z不为纯虚数,假命题;
,则 、 ,所以 且 ,C为真命
题,D为假命题;
故选:AC
10.在边长为2的正三角形 中,则( )
A. B.
C. 在 上的投影的数量为-1 D.
【答案】AB
【详解】
A:由△ 为正三角形,则 ,正确;
B: ,则 ,正确;
C: 在 上的投影的数量为 ,错误;
D: ,错误.
故选:AB
11.某高中有学生 人,其中男生 人,女生 人,希望获得全体学生的身高信息,
按照分层抽样的原则抽取了容量为 的样本.经计算得到男生身高样本均值为 ,方
差为 ;女生身高样本均值为 ,方差为 .下列说法中正确的是( )
A.男生样本量为 B.每个女生入样的概率均为C.所有样本的均值为 D.所有样本的方差为
【答案】AC
【详解】
对于A:抽样比为 ,所以样本中男生有 人,故选项A正确;
对于B:每个女生入样的概率等于抽样比 ,故选项B不正确;
对于C:由分层抽样知,样本中男生有 人,男生有 人,所有的样本均值为:
,故选项C正确;
对于D:设男生分别为 , , , ,平均数 , ,女生分别为 , ,
, ,平均数 , ,总体的平均数为 ,方差为 ,
因为
,
而 ,
所以 ,
同理可得 ,
所以 ,
故选项D不正确;
故选:AC
12.如图,已知正方体 的棱长为2,则下列四个结论正确的是( )A.直线 与 为异面直线 B. 平面
C.三棱锥 的表面积为 D.三棱锥 的体积为
【答案】ABC
【详解】
对选项A,因为 平面 , 平面 , 面 ,
,所以直线 与 为异面直线.故选项A正确;
对选项B,因为 , ,所以四边形 是平行四边形,
所以 , 平面 , 平面 ,所以 平面 ,故选项B
正确;
对选项C,
所以三棱锥 的表面积为 ,故选项C正确;
对选项D, ,故选项D错误.
故选:ABC.
三、填空题(每小题5分,共计20分)
13. , , ,则 在 上投影的数量为______.
【答案】 ##
【详解】
,
则 在 上投影的数量为
故答案为:
14.一个数字不重复的三位数的百位、十位、个位上的数字依次记为 , , ,当且仅
当 , , 中有两个不同数字的和等于剩下的一个数字时,称这个三位数为“有缘数”
(如213,341等).现从1,2,3,4这四个数字中任取三个数组成一个数字不重复的三
位数,则这个三位数为“有缘数”的概率是______.【答案】 ##
【详解】
解:从1,2,3,4这四个数字中任取三个数组成一个数字不重复的三位数的个数为
,
1,2,3,4这四个数字中两个的和等于第三个的有123,134,因此“有缘数”个数为
,
所以这个三位数为“有缘数”的概率 .
故答案为: .
15.如图,要测量底部不能到达的某铁塔 的高度,在塔的同一侧选择C,D两观测点,
且在C,D两点测得塔顶的仰角分别为 .在水平面上测得 ,C,D两
地相距 ,则铁塔 的高度是_______m.
【答案】600
【详解】
设 m,则 ,
在 中,由余弦定理可得: ,
∴ ,
解得 (m),( 舍去).
故答案为:600.
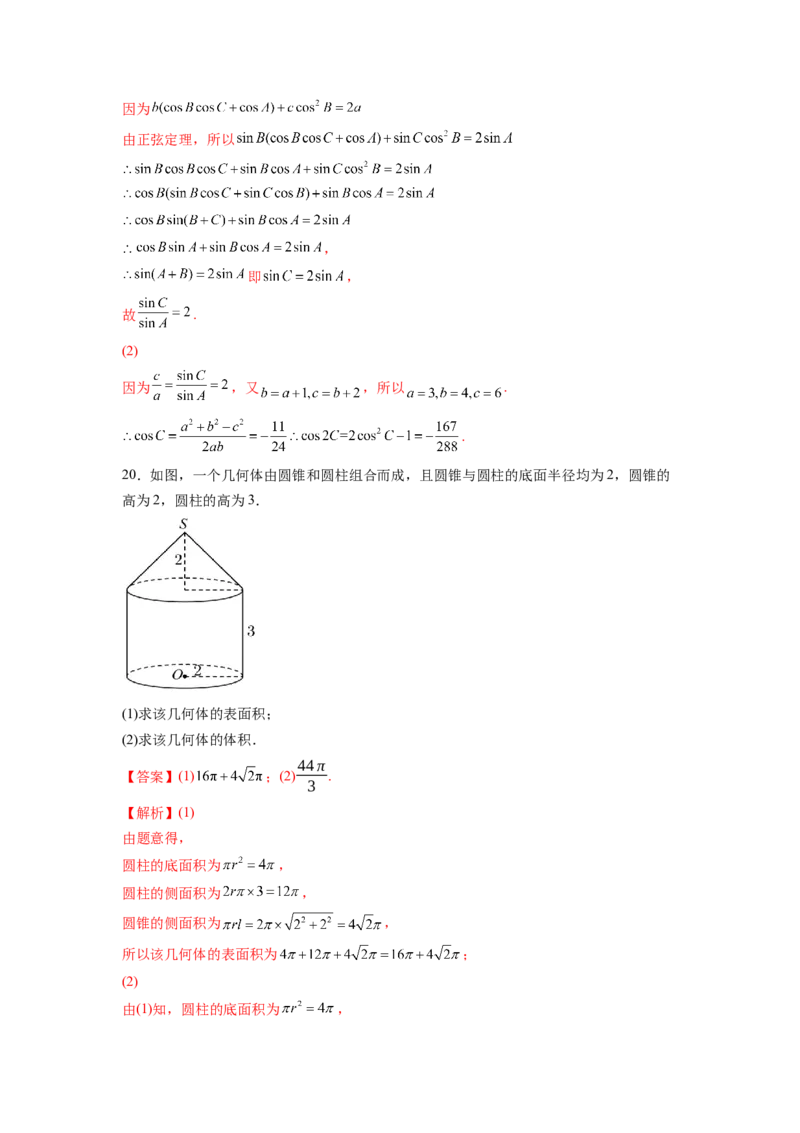
16.有一个封闭的正三棱柱容器,高为 ,内装水若干(如图1,底面处于水平状态),
将容器放倒(如图2,一个侧面处于水平状态),这时水面与各棱交点 、 、 、 分
别为所在棱的中点,则图1中水面的高度为_______.【答案】
【详解】
设正三棱柱 的底面边长为 ,则 ,
在图1中,设水面的高度为 ,则水的体积为 ,
在图2中,易知几何体 为直棱柱,
因为 为等边三角形,且 、 分别为 、 的中点,
则 ,且 ,则 是边长为 的等边三角形,
且 ,
则水的体积为 ,解得 .
故答案为: .
四、解答题(解答题需写出必要的解题过程或文字说明,共70分)
17.已知复数 ( 是虚数单位), .
(1)若 是纯虚数,求 的值;
(2)若复数 在复平面内对应的点位于第一象限,求 的取值范围.
【答案】(1) ;(2) .
【解析】(1)
复数
,∵ 是纯虚数,∴ ,
解得 ,
∴ 的值为 .
(2)
∵复数 在复平面内对应的点 位于第一象限,
∴ ,
解得 ,
∴ 的取值范围是 .
18.已知向量 , .
(1)求向量 , 的夹角的余弦值;
(2)若 ,且 与 的夹角为钝角,求 的取值范围.
【答案】(1) (2)
【解析】(1)
.
(2)
, ,由 得 ,
由 得 , ,
因为 与 的夹角为钝角, 的取值范围为 .
19. 内角A,B,C的对边分别为 , , ,且 .
(1)求 的值;
(2)若 ,求 的值.
【答案】(1)2(2)
【解析】(1)因为
由正弦定理,所以
,
即 ,
故 .
(2)
因为 ,又 ,所以 .
.
20.如图,一个几何体由圆锥和圆柱组合而成,且圆锥与圆柱的底面半径均为2,圆锥的
高为2,圆柱的高为3.
(1)求该几何体的表面积;
(2)求该几何体的体积.
44π
【答案】(1) ;(2) .
3
【解析】(1)
由题意得,
圆柱的底面积为 ,
圆柱的侧面积为 ,
圆锥的侧面积为 ,
所以该几何体的表面积为 ;
(2)
由(1)知,圆柱的底面积为 ,所以圆柱的体积为 ,
圆锥的体积为 ,
故该几何体的体积为 .
21.我国是世界上严重缺水的国家之一,为提倡节约用水,我市为了制定合理的节水方案,
对家庭用水情况进行了调查,通过抽样,获得了2021年 100个家庭的月均用水量(单位:
t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图所
示的频率分布直方图.
(1)求全市家庭月均用水量不低于 4t的频率;
(2)假设同组中的每个数据都用该组区间的中点值代替,求全市家庭月均用水量平均数的估
计值(精确到0.01);
(3)求全市家庭月均用水量的75%分位数的估计值(精确到0.01).
【答案】(1) (2)4.92 t.(3)
【解析】(1)
由直方图可知全市家庭月均用水量不低于 4t的频率为: .
(2)
因为 .
因此全市家庭月均用水量的平均数估计值为4.92 t.
(3)
频率分布直方图中,用水量低于2 t的频率为 .
用水量低于4 t的频率为 .
用水量低于6 t的频率为 .
用水量低于8 t的频率为 .
故全市家庭月均用水量的75%分位数的估计值为 ,则
则 ,解得
所以全市家庭月均用水量的75%分位数的估计值为22.如图,在平行六面体ABCD﹣ABC D 中,底面ABCD为菱形,AC 和BD 相交于点
1 1 1 1 1 1
O,E为CC 的中点
1
(1)求证:OE∥平面ABCD;
(2)若平面BDD B⊥平面ABCD,求证:DE=BE.
1 1 1
【解析】(1)
证明:如图,连接AC, ,
因为AB∥C D,AB=C D,
1 1 1 1
所以四边形 为平行四边形,
所以O为BD 和AC 的中点,
1 1
又因为E为CC 的中点,所以OE为△ACC 的中位线,所以OE∥AC,
1 1
又因为 平面ABCD,AC 平面ABCD,
所以OE∥平面ABCD;
⊂
(2)
证明:因为四边形ABCD为菱形,所以AC⊥BD,
因为平面BDD B⊥平面ABCD,平面BDD B∩平面ABCD=BD,AC 平面ABCD,
1 1 1 1
所以AC⊥平面BDD B,
1 1 ⊂
因为BD 平面BDD B,所以AC⊥BD,
1 1 1 1
又因为OE∥AC,所以OE⊥BD,
⊂ 1
因为OB=OD ,
1
所以DE=BE.
1