文档内容
7.5 正态分布 ---B提高练
一、选择题
1.(2021·广东广州市高二月考)在某次数学测试中,学生成绩 服从正态分布 ,
若 在 内的概率为0.6,则任意选取两名学生的成绩,恰有一名学生成绩不高于80的概率
为( )
A.0.16 B.0.24 C.0.32 D.0.48
【答案】C
【详解】解: 服从正态分布 , 曲线的对称轴是直线 ,
在 内取值的概率为0.6, 在 内取值的概率为0.3,
在 内取值的概率为 .现任意选取两名学生的成绩,恰有一名学生成绩
不高于80的概率 ,故选:C
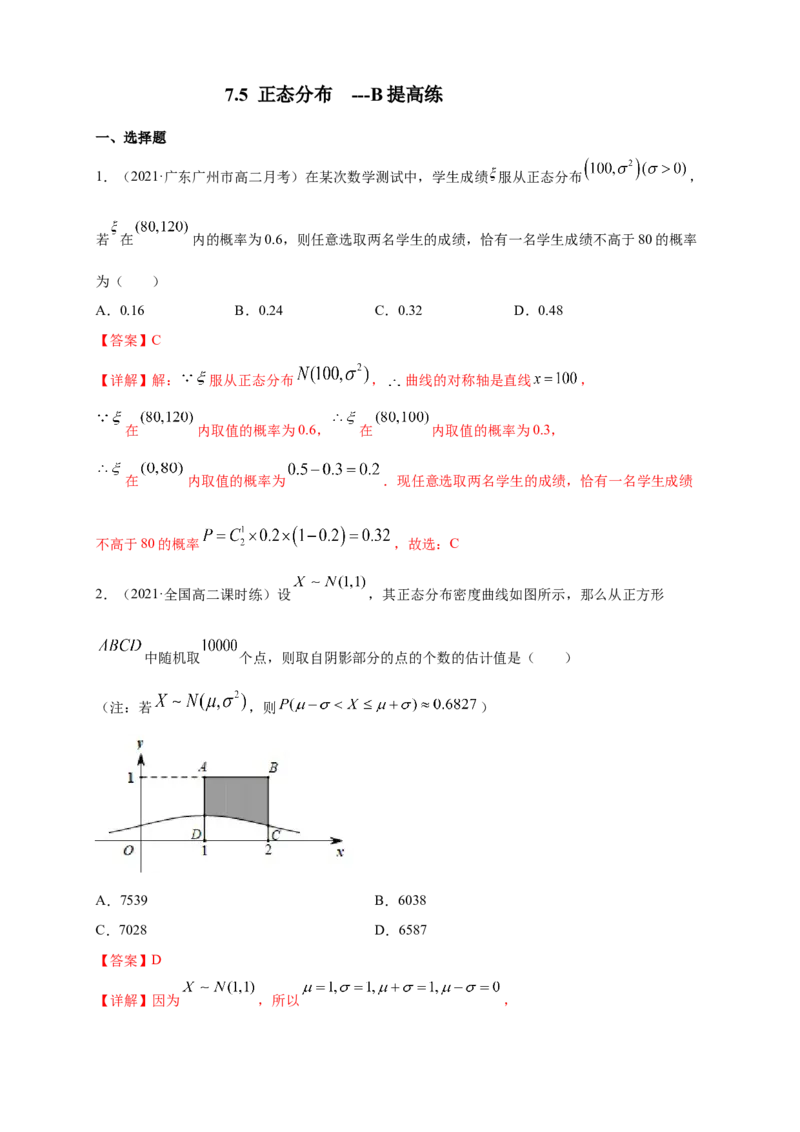
2.(2021·全国高二课时练)设 ,其正态分布密度曲线如图所示,那么从正方形
中随机取 个点,则取自阴影部分的点的个数的估计值是( )
(注:若 ,则 )
A.7539 B.6038
C.7028 D.6587
【答案】D
【详解】因为 ,所以 ,又因为 ,所以 , ,
所以阴影部分的面积为 ,所以从正方形 中随机取 个点,则取
自阴影部分的点的个数的估计值是 ,故选:D.
3.(2021·广东深圳市高二月考)已知随机变量 ,有下列四个命题:
甲: 乙:
丙: 丁:
如果只有一个假命题,则该命题为( )
A.甲 B.乙 C.丙 D.丁
【答案】D
【详解】由于乙、丙的真假性相同,所以乙、丙都是真命题,故 ,根据正态分布的对称性可
知:甲: 为真命题,所以丁为假命题.并且,
.所以假命题的是丁.故选:D
4.(2021·山东泰安一中高二月考)某工厂的一台流水线生产质量稳定可靠,已知在正常工作状态
下生产线上生产的零件内径尺寸 (单位: )服从正态分布 .甲、乙两名同学正进行尺寸
测量练习.甲、乙对各自抽取的 个零件测量零件内径尺寸(单位: )如下,甲同学测量数据: ,
, , , ;乙同学测量数据: , , , , .则可以判断( )
A.甲、乙两个同学测量都正确 B.甲、乙两个同学测量都错误
C.甲同学测量正确,乙同学测量错误 D.甲同学测量错误,乙同学测量正确
【答案】C
【详解】 , ,即 ;
甲同学测量的数据均落在 之间,测量数据正确;乙同学测量的数据中有两个数据落在之外,即小概率事件发生,知其测量错误.故选:C.
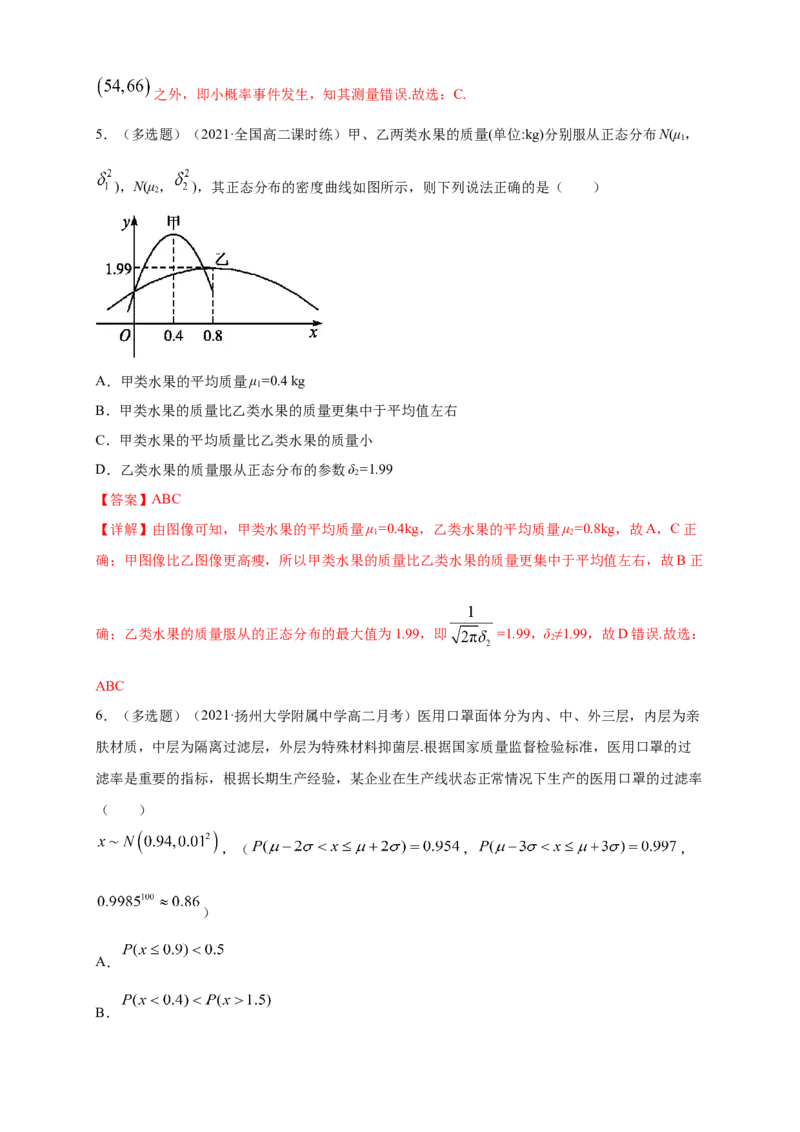
5.(多选题)(2021·全国高二课时练)甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ,
1
),N(μ, ),其正态分布的密度曲线如图所示,则下列说法正确的是( )
2
A.甲类水果的平均质量μ=0.4 kg
1
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的质量小
D.乙类水果的质量服从正态分布的参数δ=1.99
2
【答案】ABC
【详解】由图像可知,甲类水果的平均质量μ=0.4kg,乙类水果的平均质量μ=0.8kg,故A,C正
1 2
确;甲图像比乙图像更高瘦,所以甲类水果的质量比乙类水果的质量更集中于平均值左右,故B正
确;乙类水果的质量服从的正态分布的最大值为1.99,即 =1.99,δ≠1.99,故D错误.故选:
2
ABC
6.(多选题)(2021·扬州大学附属中学高二月考)医用口罩面体分为内、中、外三层,内层为亲
肤材质,中层为隔离过滤层,外层为特殊材料抑菌层.根据国家质量监督检验标准,医用口罩的过
滤率是重要的指标,根据长期生产经验,某企业在生产线状态正常情况下生产的医用口罩的过滤率
( )
,( , ,
)
A.
B.C.
D.假设生产状态正常,记 表示抽取的100只口罩中过滤率大于 的数量,则
【答案】ACD
【详解】A: ,正确;
B:因为 且 ,则
,显然 ,错误;
C: ,正确;
D: ,则 ,
由 .故选:ACD
二、填空题
7.(2021·全国高二专题练)某超市经营的某种包装优质东北大米的质量X(单位:千克)服从正态
分布N(25,0.22),任意选取一袋这种大米,质量在24.8~25.4 千克的概率为________.(附:若Z
~N(μ,σ2),则P(|Z-μ|<σ)=0.682 6,P(|Z-μ|<2σ)=0.954 4,P(|Z-μ|<3σ)=0.997 4)
【答案】0.818 5
【详解】∵X~N(25,0.22),∴μ=25,σ=0.2.
∴P(24.8≤X≤25.4)=P(μ-σ≤X≤μ+2σ)= ×(0.682 6+0.954 4)=0.341 3+0.477 2=0.818 5.
8.(2021·全国高二单元测)对一个物理量做 次测量,并以测量结果的平均值作为该物理量的最
后结果.已知最后结果的误差 ,为使误差 在 的概率不小于0.9545,至
少要测量_____次(若 ,则 ).
【答案】32【详解】根据正态曲线的对称性知:要使误差 在 的概率不小于0.9545,
则 且 , ,所以 .
9.(2021·全国高二专题练习)2019年高考前第二次适应性训练结束后,某校对全市的英语成绩进
行统计,发现英语成绩的频率分布直方图形状与正态分布 的密度曲线非常拟合.据此估
计:在全市随机抽取的4名高三同学中,恰有2名同学的英语成绩超过95分的概率是________.
【答案】
【详解】由题意,可得每名学生的英语成绩 ,所以 ,
则全市随机抽取的4名同学中恰有2名的英语成绩超过95分的概率是 .
10.(2021·湖南衡阳市八中高二月考)俗话说:“一心不能二用”,意思是我们做事情要专心,
那么,“一心”到底能否“二用”,某高二几个学生在学完《统计》后,做了一个研究,他们在本
年级随机抽取男生和女生各100名,要求他们同时做一道数学题和英语听力题,然后将这些同学完
成问题所用时间制成分布图如下,
② 男生“一心二用”所需平均时间平均值大于女生;
②所有女生“一心二用”能力都强于男生;
③女生用时众数小于男生;
④男生“一心二用”能力分布近似于正态分布.
则上述说法正确的是________.
【答案】①③④
【详解】根据图形可看出,男生“一心二用”所需平均时间平均值大于女生;并不是所有女生“一
心二用”能力都强于男生;女生用时众数小于男生;男生“一心二用”能力分布近似于正态分布;
故①③④正确.
三、解答题11.某年某省有40万考生参加高考.已知考试总分为750分,一本院校在该省计划招生6万人.经
考试后统计,考试成绩X服从正态分布 ,若以省计划招生数确定一本最低录取分数.
(1)已知 ,则该省这一年的一本最低录取分数约为多少?
(2)某公司为考生制定了如下奖励方案:所有高考成绩不低于一本最低录取分数的考生均可参加
“线上抽奖送话费”活动,每个考生只能抽奖一次.抽奖者点击抽奖按钮,即随机产生一个两位数
(10,11,…,99),若产生的两位数字相同,则可奖励20元话费,否则奖励5元,假如所有符
合条件的考生均参加抽奖活动,估计这次活动奖励的话费总额是多少?
【答案】(1)456分;(2)39万元.
【详解】
(1)X服从正态分布: ,
因为 , ;
所以 , 根据正态曲线的对称性,
,
所以 ,
若40万考生中一本院校招收6万考生,则一本院校考生占比为 ,
所以这一年一本最低录取分数为456分.
(2)X的分布列如下:
X 20 5
P 0.1 0.9
所以 ,
因为一本院校招生一共6万人,每人的话费期望值为6.5元,故总额为 万元.
12.(2021·全国高二课时练)已知某生产线的生产设备在正常运行的情况下,生产的零件尺寸
(单位: )服从正态分布 .(1)从该生产线生产的零件中随机抽取 个,求至少有一个尺寸小于 的概率;
(2)为了保证生产线正常运行,需要对生产设备进行维护,包括日常维护和故障维修,假设该生
产设备使用期限为四年,每一年为一个维护周期,每个周期内日常维护费为 元,若生产设备
能连续运行,则不会产生故障维修费;若生产设备不能连续运行,则除了日常维护费外,还会产生
一次故障维修费.已知故障维修费第一次为 元,此后每增加一次则故障维修费增加 元.
假设每个维护周期互相独立,每个周期内设备不能连续运行的概率为 .求该生产设备运行的四
年内生产维护费用总和 的分布列与数学期望.
参考数据:若 ,则 ,
, , .
【答案】(1) ;(2)分布列见解析;期望为 .
【详解】(1)因为 ,
则 , , ,
所以 ,
所以从该生产线生产的零件中随机抽取 个,至少有一个尺寸小于 的概率为:
.
(2)由题意可得 的所有可能取值为 , , , , ,
,
,,
,
,
所以 的分布列为:
数学期望