文档内容
7.4.2超几何分布 ---A基础练
一、选择题
1.在15个村庄中,有7个村庄交通不方便,若用随机变量X表示任选10个村庄中交通不方便的
村庄的个数,则X服从超几何分布,其参数为( )
A.N=15,M=7,n=10 B.N=15,M=10,n=7
C.N=22,M=10,n=7 D.N=22,M=7,n=10
【答案】A
【详解】根据超几何分布概率模型知选A.
2.(2021·石家庄市正中实验中学高二月考)有10件产品,其中3件是次品,从中任取两件,若X
表示取得次品的个数,则 等于( )
A. B. C. D.
【答案】D
【详解】 ,故选:D
3.(2021·安徽省蚌埠第三中学高二月考)校要从10名候选人中选2名同学组成学生会,其中高二
(1)班有4名候选人,假设每名候选人都有相同的机会被选到,若 表示选到高二(1)班的候
选人的人数,则 ( )
A. B. C. D.
【答案】D
【详解】超几何分布列如下
,
0 1 2.
4.(2021·黑龙江实验中学高二月考)在中国共产党建党100年之际,我校团委决定举办“鉴史知
来"读书活动,经过选拔,共10人的作品被选为优秀作品,其中高一年级5人,高二年级5人,现
采取抽签方式决定作品播出顺序,则高二年级5名同学的作品在前7顺位全部被播放完的概率为(
)
A. B. C. D.
【答案】A
【详解】由题意知:若 表示抽到高二年级同学的作品数,则服从 ,可类比:在
含有5件次品的10件商品中取7次,恰好将5件次品全部取出的概率,即 ,
∴ .故选:A.
5.(多选题)(2021·江苏高二)一个袋中有 个同样大小的黑球,编号为 ,还有 个
同样大小的白球,编号为 .现从中任取 个球,下列变量服从超几何分布的是( )
A. 表示取出的最大号码
B. 表示取出的最小号码
C.取出一个黑球记 分,取出一个白球记 分, 表示取出的 个球的总得分
D. 表示取出的黑球个数
【答案】CD
【详解】AB不符合超几何分布的定义,无法用超几何分布的数学模型计算概率,即AB错;
CD选项符合超几何分布的定义,将黑球视作次品,白球视作正品,则可以用超几何分布的数学模
型计算概率,即CD正确;故选:CD.
6.(多选题)(2021·山东淄博市高二期末)在一个袋中装有质地大小一样的 黑球, 个白球,
现从中任取 个小球,设取出的 个小球中白球的个数为 ,则下列结论正确的是( )
A. B.随机变量 服从二项分布C.随机变量 服从超几何分布 D.
【答案】ACD
【详解】由题意知随机变量 服从超几何分布,故B错误,C正确;随机变量 的所有可能为 ,
, , , , , , ,
, ,
故 ,故A,D正确.故选:ACD.
二、填空题
7.(2021·江苏省海头高级中学高二月考)一批产品共50件,有5件次品,其余均为合格品.从这
批产品中任意抽取2件,出现次品的概率为________.
【答案】
【详解】设抽取的2件产品中次品的件数为X,则P(X=k)=(k=0,1,2).所以P(X>0)=P(X=1)+
P(X=2)=+=.
8.(2021·山东淄博市高二期末)在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2
瓶,则至少取到1瓶已过保质期的概率为________.(结果用最简分数表示)
【答案】
【详解】从这30瓶饮料中任取2瓶.设至少取到1瓶已过保质期为事件A,则P(A)=+=.
9.(2021·沈阳市·辽宁实验中学高二)一袋中有除颜色不同其他都相同的2个白球,2个黄球,1
个红球,从中任意取出3个,有黄球的概率是______,若 表示取到黄球球的个数,则
______.
【答案】 ;
【详解】一袋中有除颜色不同其他都相同的2个白球,2个黄球,1个红球,
从中任意取出3个,基本事件总数n= =10,
其中有黄球包含的基本事件个数m= =9.∴有黄球的概率是p= = .
ξ表示取到黄球的个数,则ξ的所有可能取值为0,1,2,P(ξ=0)= = ,P(ξ=1)= = ,
P(ξ=2)= = ,∴E(ξ)=0× = .
10.(2021·全国高二专题练习)10名同学中有a名女生,若从中抽取2个人作为学生代表,恰好抽取
16
1名女生的概率为 ,则a=________.
45
【答案】2或8
【详解】根据题意,得16 = C 1 1 0-a C1 a,解得a=2或a=8.
45 C2
10
三、解答题
11.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其
范围是[0,10],分别有五个级别:T∈[0,2)为畅通;T∈[2,4)为基本畅通;T∈[4,6)为轻度拥堵;
T∈[6,8)为中度拥堵;T∈[8,10]为严重拥堵.晚高峰时段,从某市交通指挥中心选取了市区20个交
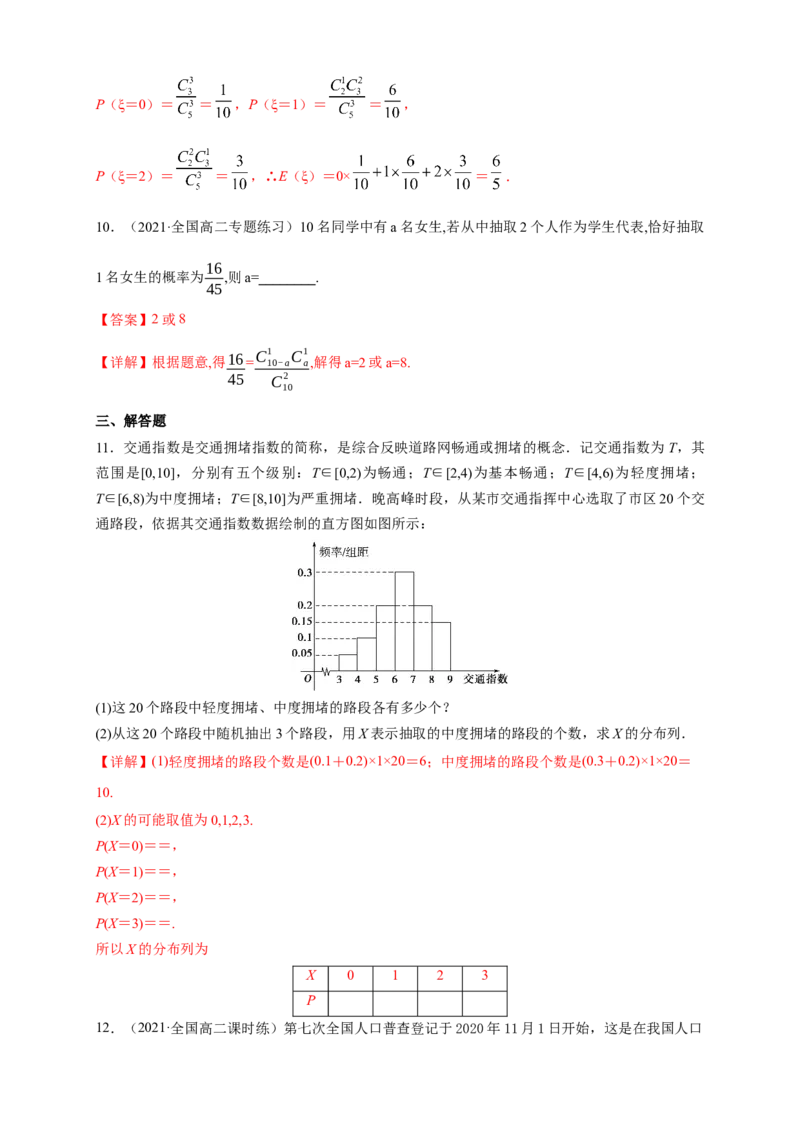
通路段,依据其交通指数数据绘制的直方图如图所示:
(1)这20个路段中轻度拥堵、中度拥堵的路段各有多少个?
(2)从这20个路段中随机抽出3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列.
【详解】(1)轻度拥堵的路段个数是(0.1+0.2)×1×20=6;中度拥堵的路段个数是(0.3+0.2)×1×20=
10.
(2)X的可能取值为0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==.
所以X的分布列为
X 0 1 2 3
P
12.(2021·全国高二课时练)第七次全国人口普查登记于2020年11月1日开始,这是在我国人口发展进入关键期开展的一次重大国情国力调查,可以为编制“十四五”规划,为推动高质量发展,
完善人口发展战略和政策体系、促进人口长期均衡发展提供重要信息支持,本次普查主要调查人口
和住户的基本情况.某校高三一班共有学生54名,按人口普查要求,所有住校生按照集体户进行申
报,所有非住校生(走读生及半走读生)按原家庭申报,已知该班住校生与非住校生人数的比为
,住校生中男生占 ,现从住校生中采用分层抽样的方法抽取7名同学担任集体户户主进行
人口普查登记.
(1)应从住校的男生、女生中各抽取多少人?
(2)若从抽出的7名户主中随机抽取3人进行普查登记培训
①求这3人中既有男生又有女生的概率;
②用 表示抽取的3人中女生户主的人数,求随机变量 的分布列与数学期望.
【答案】(1)男生、女生就分别抽取4人,3人;(2)① ;②分布列答案见解析,数学期望:
.
【详解】
(1)由已知住校生中男生占 ,则女生占 ,由于采用分层抽样的方法从中抽取7人,因此男生、
女生就分别抽取4人,3人.
(2)①设事件A为“抽取的3名户主中既有男生,又有女生”,设事件B为“抽取的3名户主中
男生有1人,女生有2人”;事件C为“抽取的3名户主中男生有2人,女生有1人”,则
A=B∪C,且B与C互斥,
= , = ,故 ,
所以,事件A发生的概率为 .
②随机变量X的所有可能取值为0,1,2,3,.随机变量X的分布列为
X 0 1 2 3
随机变量X的数学期望 .