文档内容
8.3 分类变量与列联表 ---B提高练
一、选择题
1.(2021·全国高二课时练)在一次独立性检验中,得出列联表如下:
A 合计
B 200 800 1 000
180 a 180+a
合计 380 800+a 1 180+a
且最后发现,两个分类变量A和B没有任何关系,则a的可能值是( )
A.200 B.720 C.100 D.180
2.(2021·江苏高二专题练习)为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性
别的关系,运用2×2列联表进行独立性检验,经计算得x2=7.01,则认为“喜欢乡村音乐与性别有
关系”的把握约为( )
α 0.1 0.05 0.01 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828
α
A.0.1% B.1% C.99% D.99.9%
3.(2021·江苏盐城市高二月考)某词汇研究机构为对某城市人们使用流行语的情况进行调查,随
机抽取了200人进行调查统计得下方的 列联表.则根据列联表可知( )
年轻人 非年轻人 总计
经常用流行用 125 25 150
不常用流行用语 35 15 50
总计 160 40 200
参考公式:独立性检验统计量 ,其中 .
下面的临界值表供参考:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828A.有95%的把握认为“经常用流行用语”与“年轻人”有关系
B.没有95%的把握认为“经常用流行用语”与“年轻人”有关系
C.有97.5%的把握认为“经常用流行用语”与“年轻人”有关系
D.有97.5%的把握认为“经常用流行用语”与“年轻人”没有关系
4.(2021·河南信阳市高二月考)某医疗研究所为了检验新开发的流感疫苗对流感的预防作用,根
据1000名注射了疫苗的人与另外1000名未注射疫苗的人半年的感冒记录作出如下的 的列联表,
并提出假设 “这种疫苗不能起到预防流感的作用”’则下列说法正确是( )
患流感 未患流感 合计
注射疫苗 200 800 1000
未注射疫苗 260 740 1000
合计 460 1540 2000
附: .
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
A.这种疫苗能起到预防流感的有效率为99%;
B.若某人未使用该疫苗,则他在半年中有超过99%的可能性得流感;
C.有1%的把握认为“这种疫苗能起到预防流感的作用”;
D.有99%的把握认为“这种疫苗能起到预防流感的作用”.
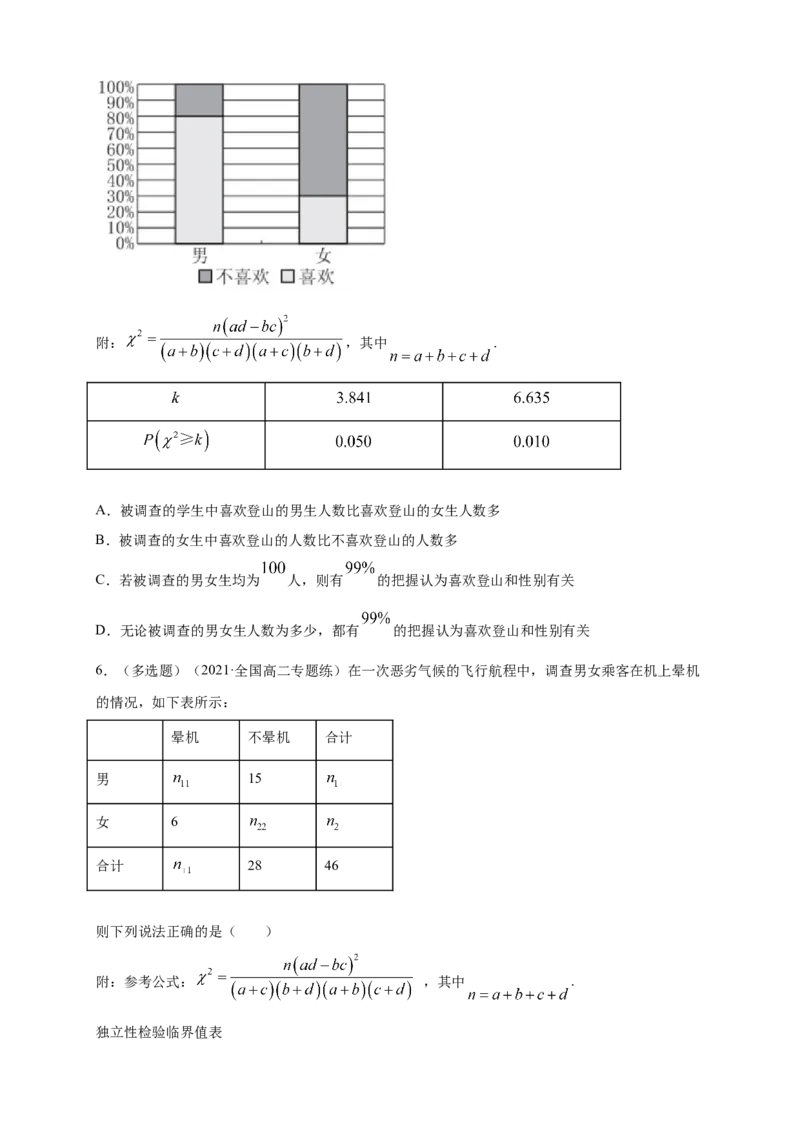
5.(多选题)(2021·山东泰安一中高二月考)为了增强学生的身体素质,提高适应自然环境、克
服困难的能力,某校在课外活动中新增了一项登山活动,并对“学生喜欢登山和性别是否有关”做
了一次调查,其中被调查的男女生人数相同,得到如图所示的等高条形统计图,则下列说法中正确
的有( )附: ,其中 .
A.被调查的学生中喜欢登山的男生人数比喜欢登山的女生人数多
B.被调查的女生中喜欢登山的人数比不喜欢登山的人数多
C.若被调查的男女生均为 人,则有 的把握认为喜欢登山和性别有关
D.无论被调查的男女生人数为多少,都有 的把握认为喜欢登山和性别有关
6.(多选题)(2021·全国高二专题练)在一次恶劣气候的飞行航程中,调查男女乘客在机上晕机
的情况,如下表所示:
晕机 不晕机 合计
男 15
女 6
合计 28 46
则下列说法正确的是( )
附:参考公式: ,其中 .
独立性检验临界值表0.10 0.05 0.025 0.010
2.706 3.841 5.024 6.635
A.
B.
C.有 的把握认为,在恶劣气候飞行中,晕机与否跟男女性别有关
D.没有理由认为,在恶劣气候飞行中,晕机与否跟男女性别有关
二、填空题
7.(2021·河南濮阳市高二期末)下表是不完整的 列联表,其中 , ,则
______.
总计
55
总计 120
8. (2021·山东高二专题练习)为了判断某高中学生是否选修文科与性别的关系,现随机抽取50名
学生,得到如下2×2列联表:
理科 文科
男 13 10
女 7 20
已知P(x2≥3.841)≈0.05,P(x2≥6.635)≈0.01.根据表中数据,得到x2= ≈4.844,
则认为选修文科与性别有关系出错的概率约为________.
9.(2021·江苏高二专题练习)某卫生机构对366人进行健康体检,有阳性家族史者糖尿病发病的
有16例,不发病的有93例,有阴性家族史者糖尿病发病的有17例,不发病的有240例,认为糖尿
病患者与遗传有关系的概率约为________.参考数据:P(x2≥3.841)≈0.05,P(x2≥6.635)≈0.01.10.(2021·河南郑州市高二)假设有两个分类变量 和 ,它们的可能取值分别为 和
,其 列联表如表,对于以下数据,对同一样本能说明 和 有关系的可能性最大的
一组为______.
① ②
③ ④
总计
总计
三、解答题
11.(2020·江苏南京市高三期中)在20人身上试验某种血清对预防感冒的作用,把他们一年中是否
患感冒的人数与另外20名未用血清的人是否患感冒的人数作比较,结果如下表所示.
未感冒 感冒
使用血清 17 3
未使用血清 14 6
(1)从上述患过感冒的人中随机选择4人,以进一步研究他们患感冒的原因.记这4人中使用血
清的人数为 ,试写出 的分布列;
(2)有多大的把握得出“使用该种血清能预防感冒”的结论?你的结论是什么?请说明理由.
附:对于两个研究对象Ⅰ(有两类取值:类A,类B)和Ⅱ(有两类取值:类1,类2)统计数据的
一个2×2列联表:
Ⅱ
类1 类2
类A
Ⅰ
类B有 ,其中 .
临界值表(部分)为
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.445 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
12.(2021·江苏南通高二月考)学生视力不良问题突出,是教育部发布的我国首份《中国义务教
育质量监测报告》中指出的众多现状之一.习近平总书记作出重要指示,要求全社会都要行动起来,
共同呵护好孩子的眼睛,让他们拥有一个光明的未来.为了落实总书记指示,掌握基层情况,某单
位调查了某校学生的视力情况,随机抽取了该校100名学生(男生50人,女生50人),统计了他们
的视力情况,结果如下:
不近视 近视
男生 25 25
女生 20 30
(1)是否有 的把握认为近视与性别有关?
附: ,其中 .
2.072 2.706 3.841 5.024 6.635 7.879 10.828
0.15 0.10 0.05 0.025 0.010 0.005 0.001
(2)如果用这100名学生中男生和女生近视的频率分别代替该校男生和女生近视的概率,且每名
学生是否近视相互独立.现从该校学生中随机抽取4人(2男2女),设随机变量 表示4人中近视的
人数,试求 的分布列及数学期望 .