文档内容
8.1 成对数据的相关关系 ---A基础练
一、选择题
1.下列现象中线性相关程度最强的是( )
A.商店的职工人数与商品销售额之间的线性相关系数为0.87
B.流通费用率与商业利润率之间的线性相关系数为-0.94
C.商品销售额与商业利润率之间的线性相关系数为0.51
D.商品销售额与流通费用率之间的线性相关系数为0.70
2.(2021·福建三明一中高二月考)变量x,y的散点图如图所示,那么x,y之间的样本相关系数r
最接近的值为( )
A.1 B.-0.5 C.0 D.0.5
3.(2021·山东泰安实验高中高二月考)一组样本数据(x ,y),(x ,y),…,(x ,y)(n≥2,x ,
1 1 2 2 n n 1
x ,…,x 不全相等)的散点图中,若所有样本点(x,y)(i=1,2,…,n)都在直线y=x+1上,则这
2 n i i
组样本数据的样本相关系数为( )
A.-1 B.0 C.0.5 D.1
4.甲、乙、丙、丁四位同学各自对x,y两变量的线性相关性作试验,求得相关系数r如表:
相关系数 甲 乙 丙 丁
r -0.82 0.78 0.69 0.87
则哪位同学的试验结果体现两变量有更强的线性相关性?( )
A.甲 B.乙 C.丙 D.丁
5.(多选题)(2021·全国高二课时练)以下两个变量成正相关的是( )
A.学生的学籍号与学生的数学成绩
B.坚持每天吃早餐的人数与患胃病的人数
C.气温与冷饮销售量
D.电瓶车的重量和行驶每千米的耗电量
6.(多选题)(2021·山东德州市高二期末)对相关系数r来说,下列说法错误的有( )
A.|r|≤1,|r|越接近0,相关程度越大;|r|越接近1,相关程度越小
B.|r|≥1,|r|越接近1,相关程度越大;|r|越大,相关程度越小
C.|r|≤1,|r|越接近1,相关程度越大;|r|越接近0,相关程度越小
D.|r|≥1,|r|越接近1,相关程度越小;|r|越大,相关程度越大
二、填空题
7.下列两个变量之间的关系是函数关系的是________.
①角度和它的余弦值;②正方形的边长和面积
③正n边形的边数和内角和;④人的年龄和身高
8.(2021·江西上饶市高二期末)某个男孩的年龄与身高的统计数据如下表所示.年龄(岁)x 1 2 3 4 5 6
身高(cm)y 78 87 98 108 115 120
其散点图如下;
则y与x (填:是或否)具有线性相关关系.
9.已知变量x和变量y的3对随机观测数据(2,2),(3,-1),(5,-7),则成对样本数据的样本相
关系数是________.
10.(2021·全国高二专题练习)已知某次考试之后,班主任从全班同学中随机抽取一个容量为8
的样本,他们的数学、物理成绩(单位:分)对应如下表:
学生编号 1 2 3 4 5 6 7 8
数学成绩 60 65 70 75 80 85 90 95
物理成绩 72 77 80 84 88 90 93 95
给出散点图如下:
根据以上信息,判断下列结论:
①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③从全班随机抽取甲、乙两名同学,若甲同学数学成绩为80分,乙同学数学成绩为60分,则甲同
学的物理成绩一定比乙同学的物理成绩高.
其中正确的个数为________.
三、解答题
11.(2021·河南高二期中)5名学生的数学和物理成绩如下表:画出散点图,并判断它们是否具有相关关系.
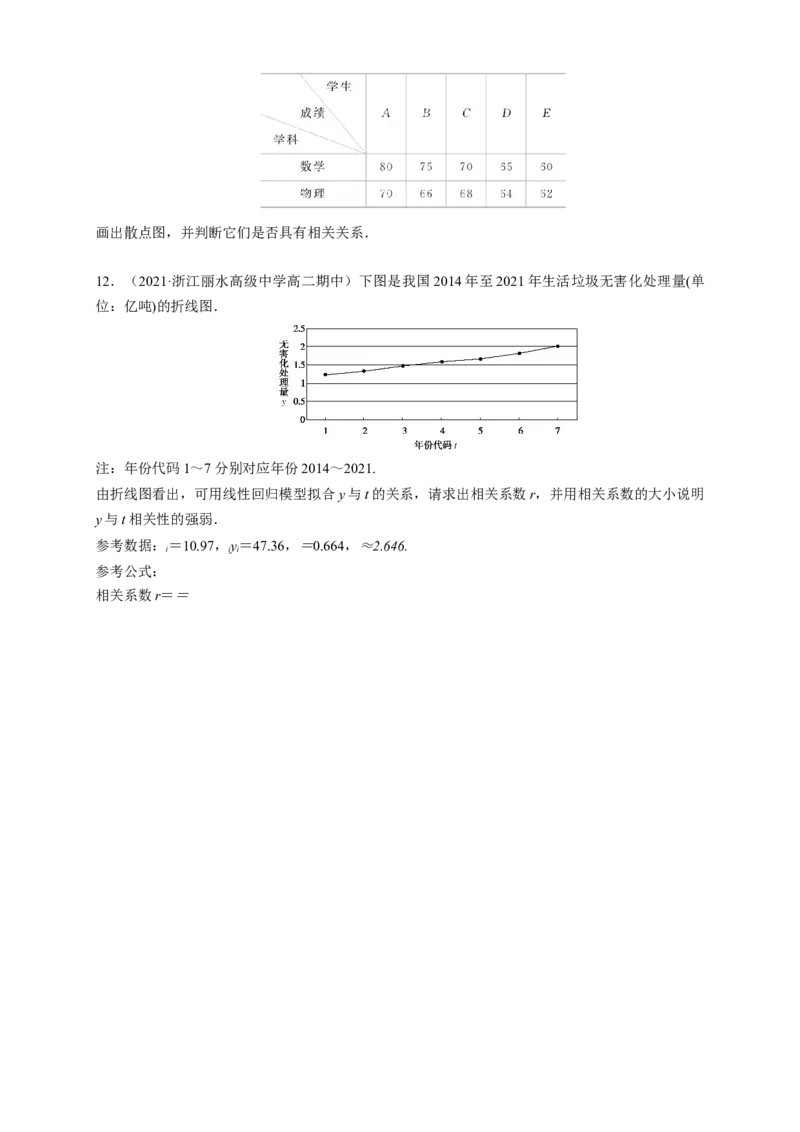
12.(2021·浙江丽水高级中学高二期中)下图是我国2014年至2021年生活垃圾无害化处理量(单
位:亿吨)的折线图.
注:年份代码1~7分别对应年份2014~2021.
由折线图看出,可用线性回归模型拟合y与t的关系,请求出相关系数r,并用相关系数的大小说明
y与t相关性的强弱.
参考数据:=10.97,y=47.36,=0.664,≈2.646.
i i i
参考公式:
相关系数r==