文档内容
8.2 一元线性回归模型及其应用 ---B提高练
一、选择题
1.(2021·全国高二课时练)某种碘是一种放射性物质,该碘最初一段时间衰减的时间 (单位:
分钟)与剩余量 (单位:克)存在着较强的线性相关关系.如表是某校化学社团师生观测该碘在
5天内衰减情况得出的一组数据,则 对 的线性回归方程可以是( )
(单
位:分 10 20 30 40 50
钟)
(单
22.5 19 17.5 15 11
位:克)
A. B. C. D.
【答案】B
【详解】根据题意数据分析得到:该碘最初一段时间衰减的时间 与剩余量 存在着较强的负线性
相关关系,假设回归方程为 ,由选项得到 ,又 ,
,所以 ,故 对 的线性回归方程为:
.
2.(2021·黑龙江哈尔滨九中高二月考)已知具有相关关系的两个随机变量的一组观测数据的散点
图分布在函数 的图象附近,设 ,将其变换后得到线性方程 ,则
( )
A. B. C. D.
【答案】B【详解】因 ,则 ,于是有
,所以 .故选:B
3.(2021·江苏徐州高二月考)对于数据组 ,如果由线性回归方程得到的对
应于自变量 的估计值是 ,那么将 称为相应于点 的残差.某工厂为研究某种产
品产量 (吨)与所需某种原材料 吨)的相关性,在生产过程中收集4组对应数据 如下表
所示:
3 4 5 6
2.5 3 4
根据表中数据,得出 关于 的线性回归方程为 ,据此计算出样本处的残差为-
0.15,则表中 的值为( )
A.3.3 B.4.5 C.5 D.5.5
【答案】B
【详解】由题意可知,在样本(4,3)处的残差-0.15,则 ,即 ,
解得 ,即 ,又 ,且线性方程过样本中心点( ,
),
则 ,则 ,解得 .故答案为:B
4.(2021·全国高二课时练习)某网店经销某商品,为了解该商品的月销量 (单位:千件)与售价
(单位:元/件)之间的关系,收集 组数据进行了初步处理,得到如下数表:根据表中的数据可得回归直线方程 ,以下说法正确的是( )
A. , 具有负相关关系,相关系数
B. 每增加一个单位, 平均减少 个单位
C.第二个样本点对应的残差
D.第三个样本点对应的残差
【答案】D
【详解】对于A选项:由相关系数绝对值的不超过1,A不正确;对于B选项:由回归直线方程知,
每增加一个单位, 平均减少 个单位,B不正确;对于C选项:第二个样本点对应的残差
,C不正确;对于D选项:第三个样本点对应的残差
,D正确.故选:D
5.(多选题)(2021·福建三明一中高二月考)某种产品的价格x(单位:元/ )与需求量y(单位:
)之间的对应数据如下表所示:
x 10 15 20 25 30
y 11 10 8 6 5
根据表中的数据可得回归直线方程 ,则以下正确的是( )
A.相关系数
B.
C.若该产品价格为35元 ,则日需求量大约为
D.第四个样本点对应的残差为
【答案】BCD【详解】解: 对A、B:由表中的数据, ,
,
将 , 代入 得 ,所以A选项错误,B选项正确;
对C:由题意 代入 得 ,所以日需求量大约为 ,
所以C选项正确;对D:第四个样本点对应的残差为 ,
所以D选项正确;故选:BCD.
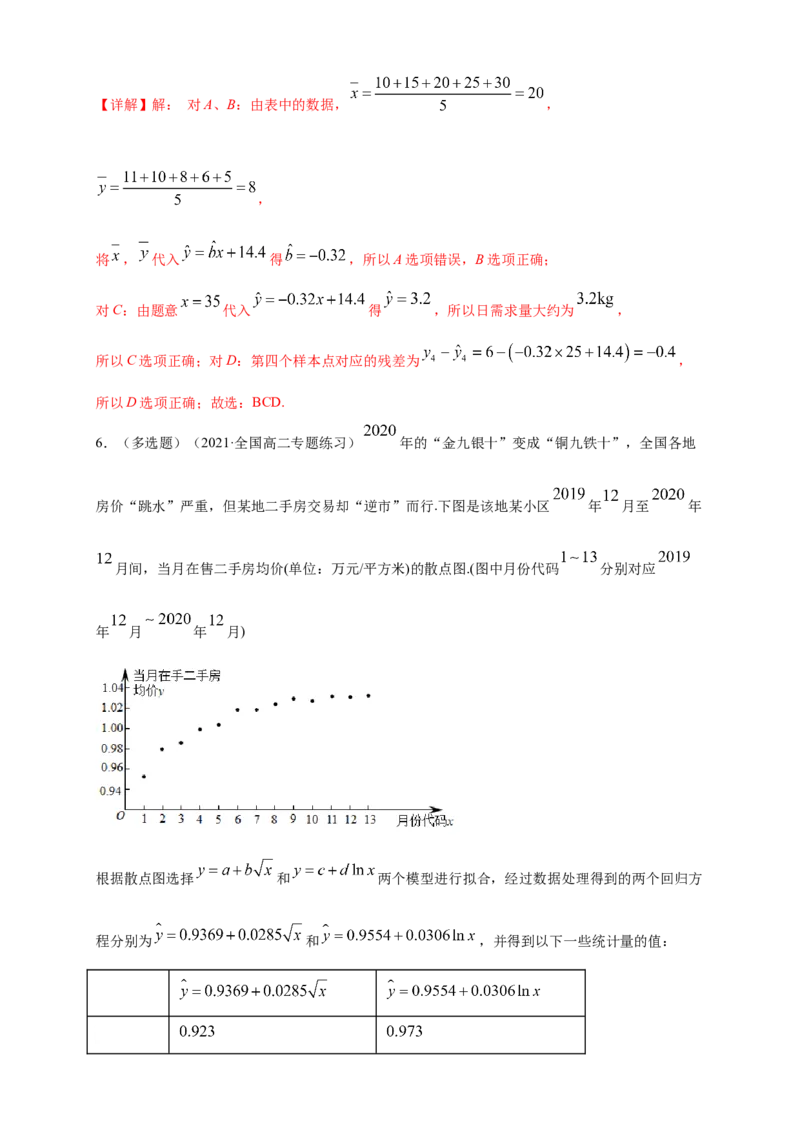
6.(多选题)(2021·全国高二专题练习) 年的“金九银十”变成“铜九铁十”,全国各地
房价“跳水”严重,但某地二手房交易却“逆市”而行.下图是该地某小区 年 月至 年
月间,当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码 分别对应
年 月 年 月)
根据散点图选择 和 两个模型进行拟合,经过数据处理得到的两个回归方
程分别为 和 ,并得到以下一些统计量的值:注: 是样本数据中 的平均数, 是样本数据中 的平均数,则下列说法正确的是( )
A.当月在售二手房均价 与月份代码 呈负相关关系
B.由 预测 年 月在售二手房均价约为 万元/平方米
C.曲线 与 都经过点
D.模型 回归曲线的拟合效果比模型 的好
【答案】BD
【详解】对于A,散点从左下到右上分布,所以当月在售二手房均价y与月份代码x呈正相关关系,
故A不正确;对于B,令 ,由,
所以可以预测2021年2月在售二手房均价约为1.0509万元/平方米,故B正确;
对于C,非线性回归曲线不一定经过 ,故C错误;
对于D, 越大,拟合效果越好,由 ,故D正确.故选:BD
二、填空题
7.(2021·江西赣州市·高二期末)下面是两个变量的一组数据:
1 2 3 4 5 6 7 8
1 9 16 25 36 49 64
这两个变量之间的线性回归方程为 ,变量 中缺失的数据是___________.
【答案】4;
【详解】设变量 中缺失的数据为 ,则 ,
,因为这两个变量之间的线性回归方程为
,所以 ,解得 .8.(2021·扶风县法门高中高二月考)已知一组数据点 , , ,…,
,用最小二乘法得到其线性回归方程为 ,若数据 , , ,… 的均值
为 ,则可以估计数据 , , ,… 的均值为______.
【答案】2
【详解】因为回归方程为 ,且数据 , , ,…, 的均值为 ,即 ,
把 ,代入回归直线方程,可得 ,所以可以估计数据 , , ,
…, 的均值为 .
9.(2021·全国高二课时练习)某单位为了落实“绿水青山就是金山银山”理念,制订节能减排的
目标,调查了用电量 (单位:千瓦·时)与气温 (单位:℃)之间的关系,随机选取了4天的用
电量与当天气温,并制作了以下对照表:
(单位:℃) 17 14 10
(单位:千瓦·
24 34 38 64
时)
由表中数据得回归直线方程为 ,则由此估计当某天气温为2℃时,当天用电量为
________千瓦·时
【答案】
【详解】由题意,根据表格中的数据,可得
,
将点 代入回归直线方程,求得 ,
所以回归直线方程为 ,当 时,代入求得 .
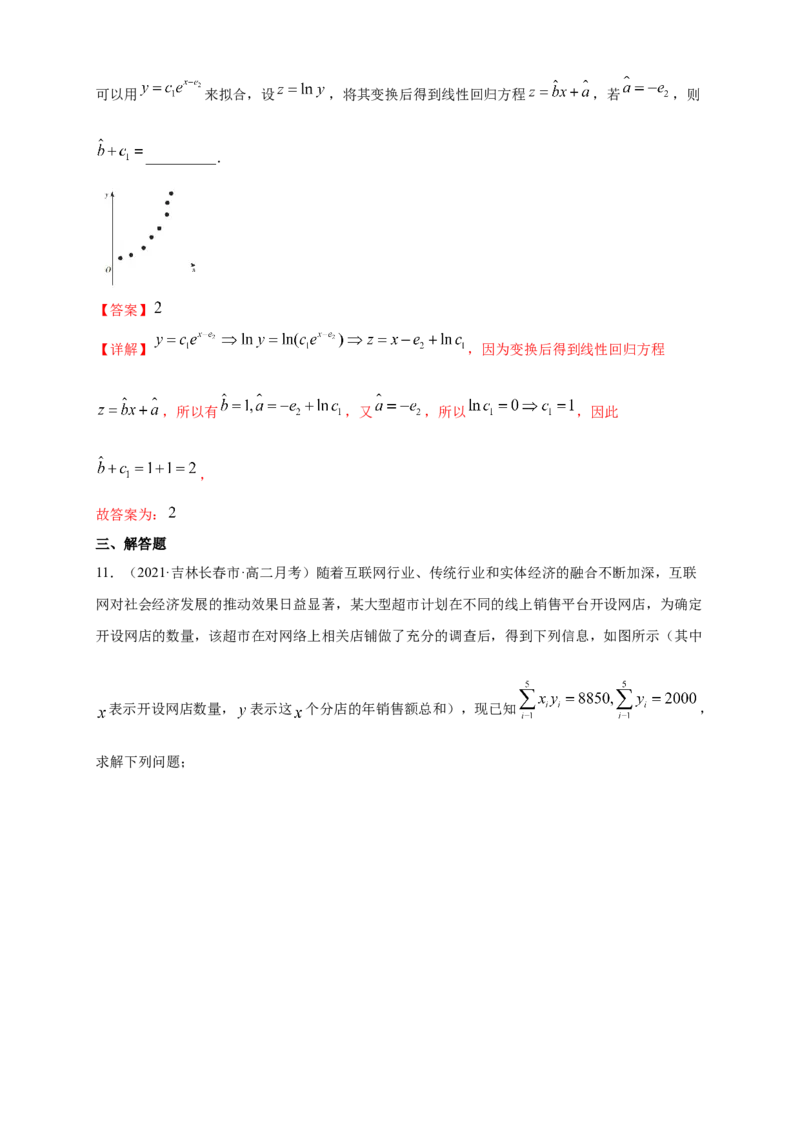
10.(2021·全国高二课时练)已知具有相关关系的两个随机变量的一组数据的散点图如图所示,可以用 来拟合,设 ,将其变换后得到线性回归方程 ,若 ,则
__________.
【答案】
【详解】 ,因为变换后得到线性回归方程
,所以有 ,又 ,所以 ,因此
,
故答案为:
三、解答题
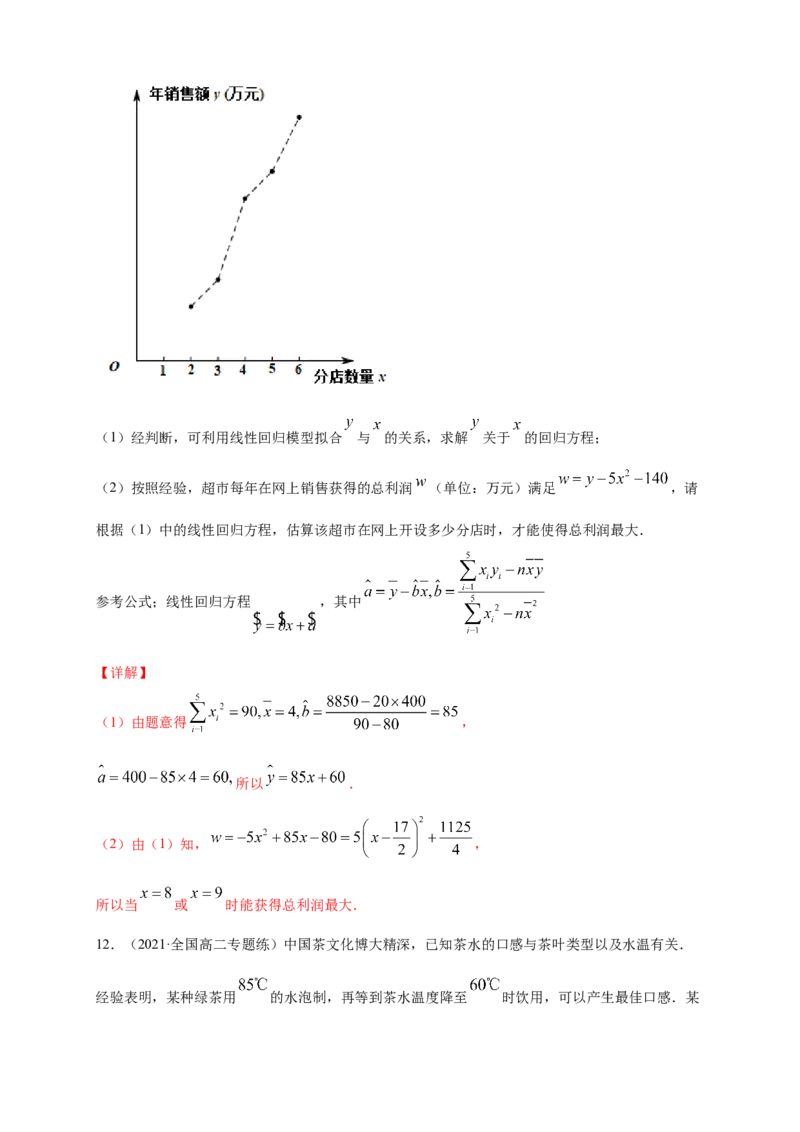
11.(2021·吉林长春市·高二月考)随着互联网行业、传统行业和实体经济的融合不断加深,互联
网对社会经济发展的推动效果日益显著,某大型超市计划在不同的线上销售平台开设网店,为确定
开设网店的数量,该超市在对网络上相关店铺做了充分的调查后,得到下列信息,如图所示(其中
表示开设网店数量, 表示这 个分店的年销售额总和),现已知 ,
求解下列问题;(1)经判断,可利用线性回归模型拟合 与 的关系,求解 关于 的回归方程;
(2)按照经验,超市每年在网上销售获得的总利润 (单位:万元)满足 ,请
根据(1)中的线性回归方程,估算该超市在网上开设多少分店时,才能使得总利润最大.
参考公式;线性回归方程 ,其中
【详解】
(1)由题意得 ,
所以 .
(2)由(1)知, ,
所以当 或 时能获得总利润最大.
12.(2021·全国高二专题练)中国茶文化博大精深,已知茶水的口感与茶叶类型以及水温有关.
经验表明,某种绿茶用 的水泡制,再等到茶水温度降至 时饮用,可以产生最佳口感.某学习研究小组通过测量,得到了下面表格中的数据(室温是 ).
泡制时间 0 1 2 3 4
水温 85 79 74 71 65
4.2 4.1 4.0 3.9 3.8
(1)小组成员根据上面表格中的数据绘制散点图,并根据散点图分布情况,考虑到茶水温度降到
室温(即 )就不能再降的事实,决定选择函数模型 来刻画.
①令 ,求出 关于 的线性回归方程;
②利用①的结论,求出 中的 与 .
(2)你认为该品种绿茶用 的水大约泡制多久后饮用,可以产生最佳口感?
参考数据: .参考公式:
.
【答案】(1)① ;② , ;(2)泡制 后饮用,口感最佳.
【解】(1)①由已知得出 与 的关系,如下表:
泡制时间
0 1 2 3 4
4.2 4.1 4.0 3.9 3.8
设线性回归方程 ,
由题意,得 ,,
,
,
则 ,
,
则 关于 的线性回归方程为 ;
②由 ,得 ,
两边取对数得, ,
利用①的结论得: ,
, ;
(3)由(1)得, ,
令 ,得 .
∴该品种绿茶用 的水泡制 后饮用,口感最佳.