数学答案-浙江省宁波市镇海中学2023-2024学年高一上学期分班考试（创新班选拔）_2024-2025高一（7-7月题库）_2024年8月试卷

2023.6.29 镇海中学新高一分班考（创新班选拔）
ab 1 a

1. 已知ab 2 ，则b 的值为_____________.
1
【答案】
3
【解析】
【分析】变形给定等式即可得解.
ab 1
【详解】由  ，得b0，2(ab)ab，整理得3ab，
ab 2
a 1
所以  .
b 3
1
故答案为：
3
2. 已知一圆锥的主视图和俯视图如图所示，则该圆锥的侧面积和侧面展开图的圆心角分别为
_____________.
6π
【答案】15π；
5
【解析】
【分析】根据题意，得到圆锥的底面圆的半径和母线，设侧面展开图的扇形所在圆的圆心角为，结合弧
长公式，列出方程，即可求解.
第5页/共22页
学科网（北京）股份有限公司【详解】根据给定的圆锥的三视图，可得圆锥的底面圆的半径为r 3，高为4，则母线长为l 5，
可圆锥的侧面积为S  πrl  π3515π，底面圆的周长为2πr 2π36π，
6π
设侧面展开图的扇形所在圆的圆心角为，则l 6π，可得56π，解得 .
5
6π
故答案为：15π； .
5
3. 如图中，O的半径为20，则阴影部分的面积为_____________.
【答案】200
【解析】
【分析】由图可知弓形 AB的面积等于扇形OAB的面积减去AOB的面积，所以阴影部分的面积等于以
10 2 为半径的半圆的面积减去弓形的面积，求解即可.
【详解】由已知 OA  OB 20，所以 AB 20 2 ，
所以 AP  BP 10 2 ，
1 1
S  2020200，扇形OAB的面积为 π202 100π，
AOB 2 4
1  2
所以阴影部分的面积为 π 10 2  100π200 200.
2
故答案为：200.
abc
4. 已知二次函数 y ax2bxc恒非负，ba 0，c0，则 的最小值为_____________.
ba
【答案】3
【解析】
【分析】根据题意，由二次函数恒非负可得a,b,c的不等关系，然后将原式化简，结合基本不等式代入计算，
即可求解.
a 0
【详解】由于二次函数 y ax2bxc恒非负，所以 ，所以4acb2，
Δ b2 4ac0
第6页/共22页
学科网（北京）股份有限公司b2
且ba 0，则c b2 ，则abc ab 4a   3a ba   2
 
4a ba ba 4a  ba 
4  ba 3a b2
  3，当且仅当3a ba,c  时，即cb4a时，等号成立，
4a  ba  4a
abc
所以 的最小值为3.
ba
故答案为：3
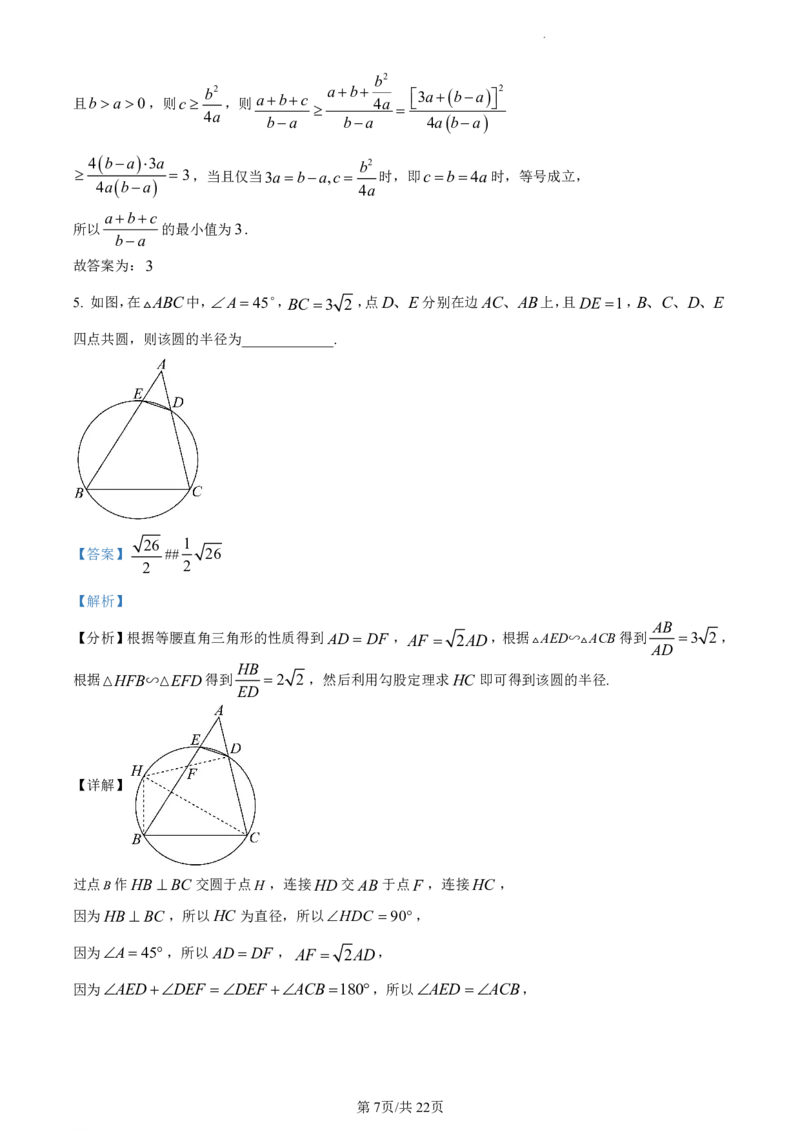
5. 如图，在ABC中，A45，BC 3 2 ，点D、E分别在边AC、AB上，且DE 1，B、C、D、E
四点共圆，则该圆的半径为_____________.
26 1
【答案】 ## 26
2 2
【解析】
AB
【分析】根据等腰直角三角形的性质得到AD  DF ，AF  2AD，根据AED∽ACB得到 3 2，
AD
HB
根据VHFB∽VEFD得到 2 2 ，然后利用勾股定理求HC 即可得到该圆的半径.
ED
【详解】
过点B作HB BC交圆于点H ，连接HD交AB于点F ，连接HC ，
因为HB BC，所以HC 为直径，所以HDC 90，
因为A45，所以AD  DF ，AF  2AD，
因为AEDDEF DEFACB180，所以AEDACB，
第7页/共22页
学科网（北京）股份有限公司CB AB
所以AED∽ACB，所以  3 2，
ED AD
在HFB和△EFD中，HFB EFD，HBF EDF （同弧所对的圆周角相等），
HB FB AB AF AB 2AD
所以VHFB∽VEFD，所以    2 2，则HB2 2 ，
ED FD AD AD
 2  2
所以HC  2 2  3 2  26 ，
26
所以该圆的半径为 .
2
26
故答案为： .
2
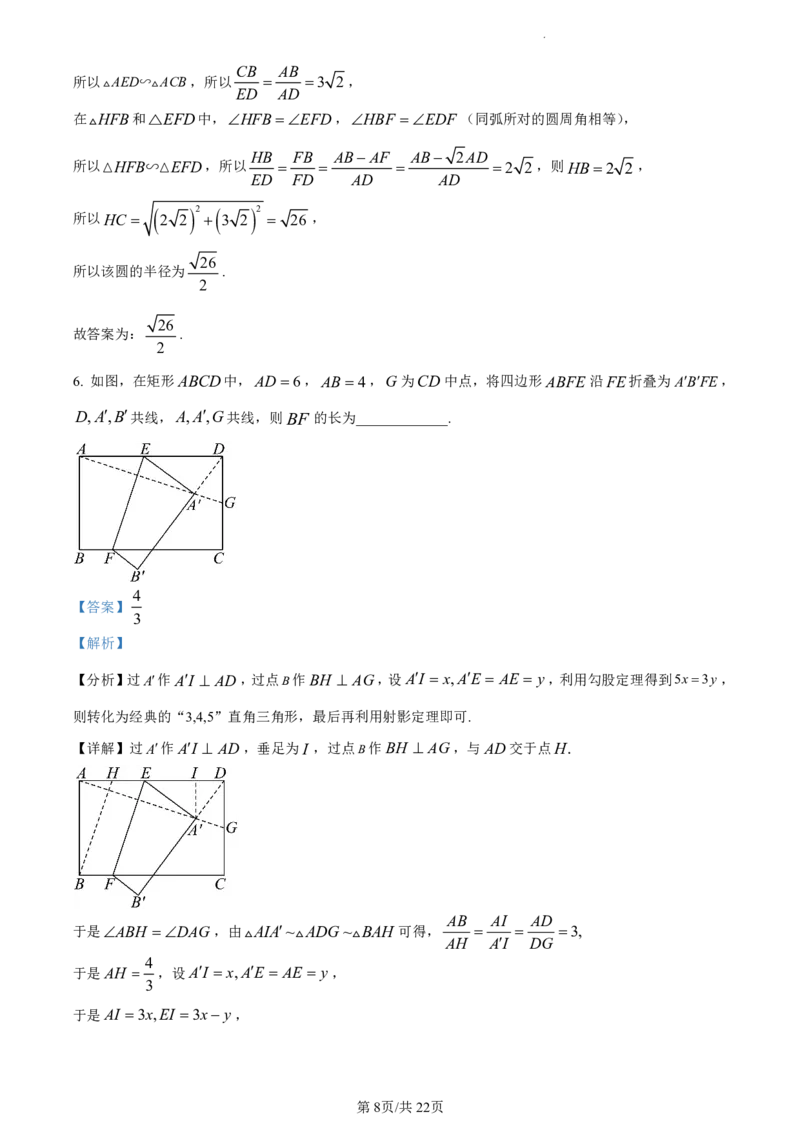
6. 如图，在矩形ABCD中，AD 6，AB 4，G为CD中点，将四边形ABFE 沿FE折叠为ABFE，
D,A,B共线，A,A,G共线，则BF 的长为_____________.
4
【答案】
3
【解析】
【分析】过A作AI  AD，过点B作BH  AG，设AI  x,AE  AE  y，利用勾股定理得到5x3y ，
则转化为经典的“3,4,5”直角三角形，最后再利用射影定理即可.
【详解】过A作AI  AD，垂足为I ，过点B作BH  AG，与AD交于点H.
AB AI AD
于是ABH DAG ，由AIA~ADG~BAH 可得，   3,
AH AI DG
4
于是AH = ，设AI  x,AE  AE  y，
3
于是AI 3x,EI 3x y，
第8页/共22页
学科网（北京）股份有限公司在AEI 中使用勾股定理x2  3x y 2  y2，解得5x3y，
记AI  x3t,EI 4t,EA5t,AI 9t，
在直角△EDA中，由射影定理，AI2 IEID ，
AI2 9t 9t 8
于是ID   ，因为AD9t 6，所以t  ,
EI 4 4 15
8
于是AE 5t  ，因为BH  AG，EF  AG，则BH //EF，
3
因为HE//BF，所以四边形BHEF为平行四边形，
8 4 4
因此BF  AEAH    .
3 3 3
4
故答案为： .
3
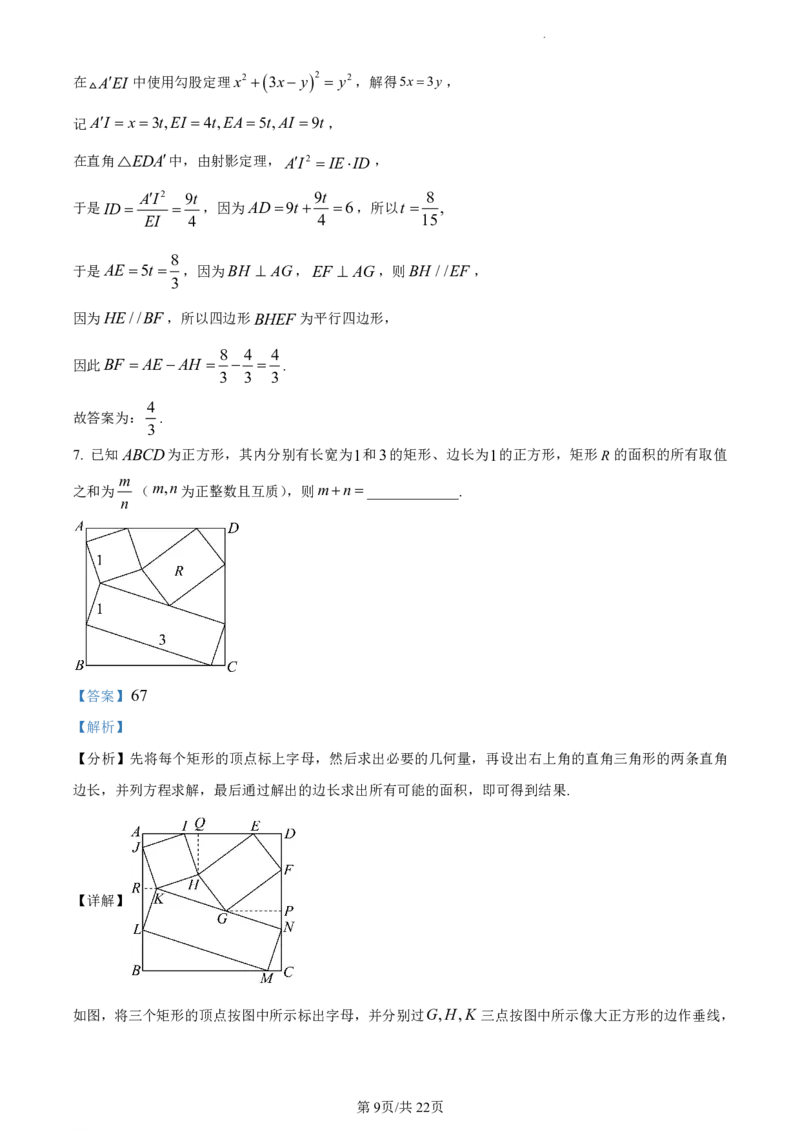
7. 已知ABCD为正方形，其内分别有长宽为1和3的矩形、边长为1的正方形，矩形R的面积的所有取值
m
之和为 （m,n为正整数且互质），则mn_____________.
n
【答案】67
【解析】
【分析】先将每个矩形的顶点标上字母，然后求出必要的几何量，再设出右上角的直角三角形的两条直角
边长，并列方程求解，最后通过解出的边长求出所有可能的面积，即可得到结果.
【详解】
如图，将三个矩形的顶点按图中所示标出字母，并分别过G,H,K 三点按图中所示像大正方形的边作垂线，
第9页/共22页
学科网（北京）股份有限公司垂足分别为P,Q,R.
设KLA，由几何关系可知：
KLAKJBAIJ BMLCNM NGPIHQ，
RKLRKJ AJI BLM CMN PNGHIQ90.
从而BC  BM MC  LM cosMNsin3cossin，
AB BLLRRJ JA LMsinKLcosKJcosIJsin
3sincoscossin2cos4sin.
1 10 3 10
所以3cossin2cos4sin，得tan ，从而sin ，cos .
3 10 10
3 10 10 3 10
故AB BC 3cossin3   10，且QH IH coscos ，
10 10 10
3 10 10 3 10
AI  IJcoscos ，IQ IHsinsin ，NC  NM coscos .
10 10 10
3 10 7 10 7 10 10 3 10
故ID ADAI  ABAI  10  ，QD IDIQ    ，
10 10 10 10 5
3 10 7 10
DN  DCNC  ABNC  10  .
10 10
由于HQE 90FPG，QEH 90DEF DFE 90GFPPGF，HE  FG，
3 10
故QHE全等于△PFG，所以PG QE，PF QH  .
10
3 10
设DE  x，DF  y，则PGQE QDDE  x.
5
3 10
QH DE 10 x  
由于QHE相似于DEF ，故  ，即  ，化简得到3y  x 6 10x .
QE DF 3 10 y
x
5
同时，有 10  DF FPPN NC
第10页/共22页
学科网（北京）股份有限公司3 10
 y PGtancos
10
3 10 13 10  3 10
 y   x
 
10 3 5 10
 
1 4 10 3 10
 y x ，即3y x .
3 5 5
  3 10 3 10  
所以有3y  x 6 10x ，3y x ，将第一式代入第二式得x  x 6 10x ，解得
5 5
3 10 10
x 或x  .
10 5
 3 10  10
x  x
3 10  10  5
再由3y x 即知 或 .
5  3 10  4 10
y  y 
 
 10  15
而矩形R的面积S  EHEF  QH2 QE2  ED2 DF2
R
2 2
3 10  3 10 
     x  x2 y2
   
10 5
   
9 6 10
  xx2  x2  y2 .
2 5
9 5
分别代入即知，矩形R的面积S  或S  .
R 5 R 3
m 9 5 52 m52
所以    ，故 ，这就得到mn521567.
n 5 3 15 n15
故答案为：67.
【点睛】关键点点睛：本题的关键点在于，利用直角三角形制造的互余关系下的相似三角形，可以得到相
似比关系，从而求得相应线段的长度.
8. 已知9个正整数的中位数和平均数均为9，众数为1，则其中最大数的最小值为_____________.
【答案】16
【解析】
【分析】根据题意，由条件可得前5个数是1,1,7,8,9，当后4个数是连续的4个正整数时，最大的数最小，
即可得到结果.
第11页/共22页
学科网（北京）股份有限公司【详解】因为中位数是9，所以将这9个正整数从小到大排列，第5个数是9，
因为众数为1，所以1至少有2个，
要使这列数的最大数最小，则其他8个数要尽量大，
所以前5个数是1,1,7,8,9，所以后4个数的和为99 11789 55 ，
当后4个数是连续的4个正整数时，最大的数最小，
设最后一个数为x，则x x1  x2  x3 55，解得x15.25，
因为xN，则x16.
故答案为：16
9. 抛物线 y  x22kxk2 向右平移 2 个单位，向上平移 1 个单位，恰好过坐标原点，则k 的值为
_____________.
【答案】5或1
【解析】
【分析】直接利用抛物线平移规律：上加下减，左加右减进而得出平移后的解析式，代入原点即可求解.
【详解】将抛物线 y  x22kxk2 向右平移2个单位，向上平移1个单位，
得到的解析式为： y  x2 2 2k  x2 k2 1，
所以 y  x2  2k4  xk2 4k5，
因为抛物线过坐标原点，
所以k2 4k50，解得k 5或k 1.
故答案为：5或1.
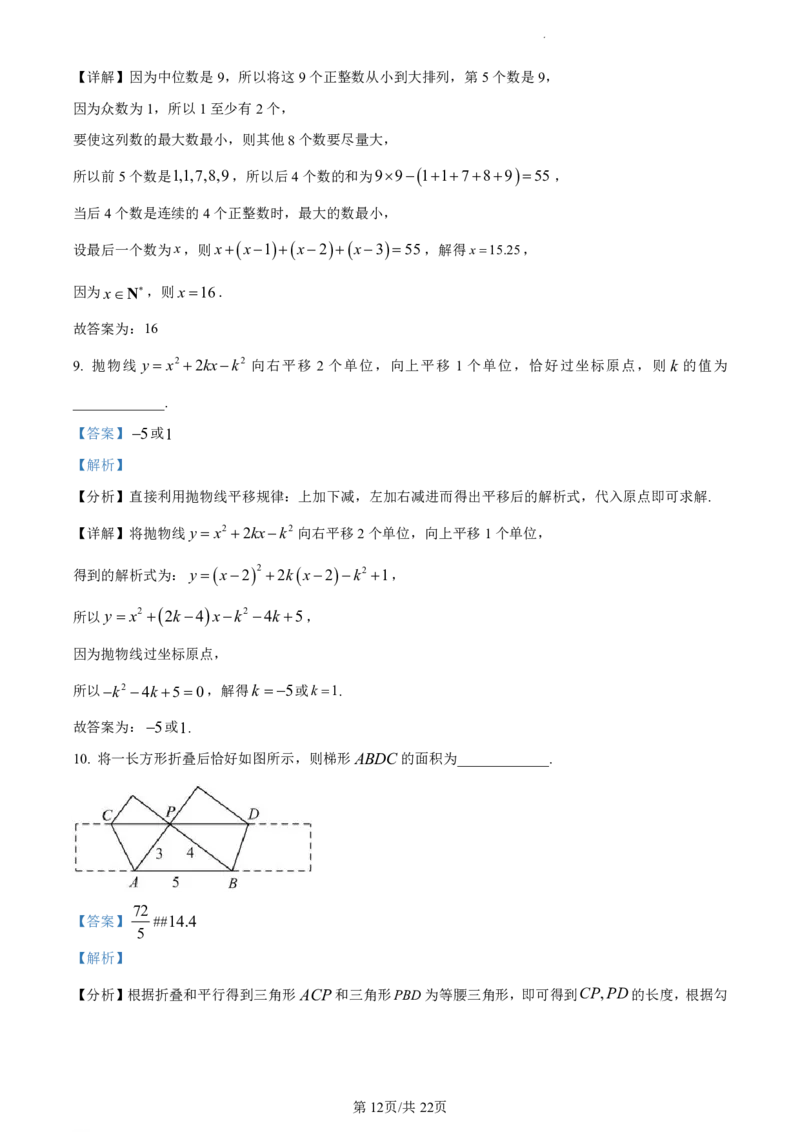
10. 将一长方形折叠后恰好如图所示，则梯形ABDC的面积为_____________.
72
【答案】 ##14.4
5
【解析】
【分析】根据折叠和平行得到三角形ACP和三角形PBD为等腰三角形，即可得到CP,PD的长度，根据勾
第12页/共22页
学科网（北京）股份有限公司股定理和等面积得到梯形的高，然后求面积即可.
【详解】
如图，过点P作PF  AB于点F ，
由题意得EAC CAP，
因为四边形ABDC 为梯形，所以ABCD，
所以PCAEAC CAP，
所以三角形ACP为等腰三角形，CP AP3，
同理可得，PD  PB 4，
因为PA2 PB2  AB2，所以PA  PB，
34 12
根据等面积的思路得到PFAB  PAPB，所以PF   ，
5 5
12
 345 
所以 5 72.
S  
ABDC 2 5
72
故答案为： .
5
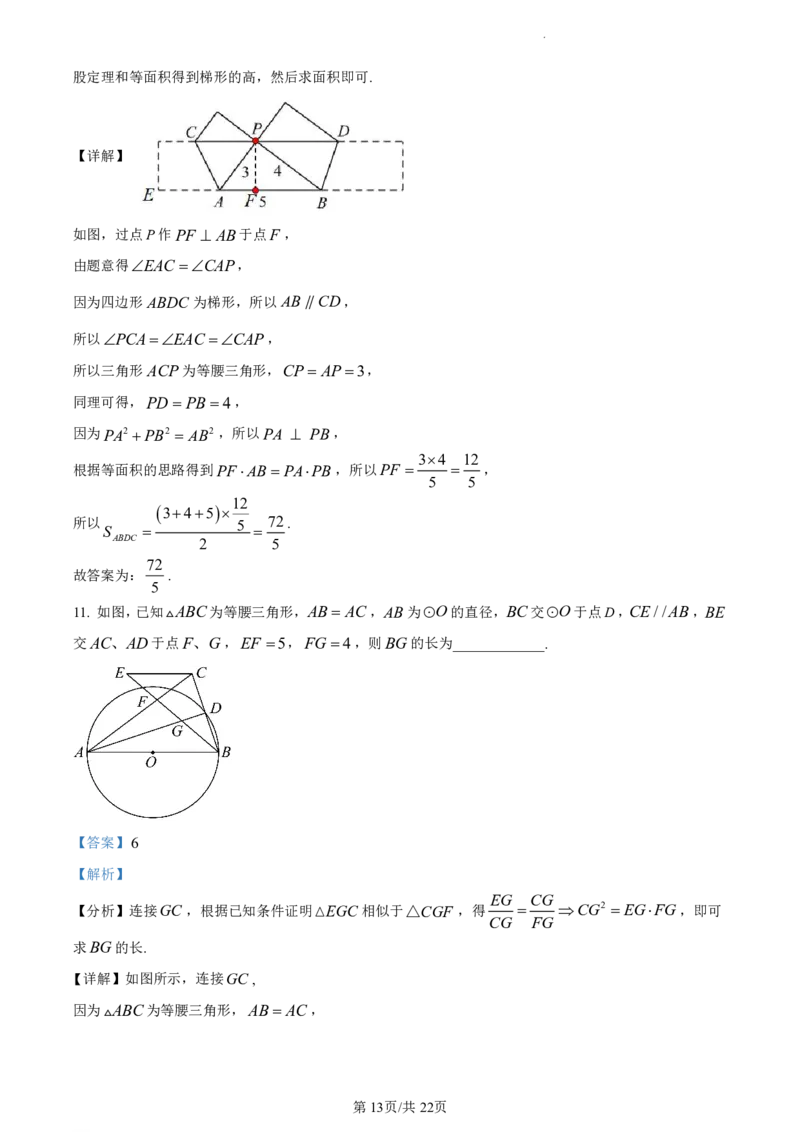
11. 如图，已知ABC为等腰三角形，AB AC，AB为O的直径，BC交O于点D，CE//AB，BE
交AC、AD于点F、G，EF 5，FG4，则BG的长为_____________.
【答案】6
【解析】
EG CG
【分析】连接GC ，根据已知条件证明VEGC相似于△CGF ，得  CG2  EGFG，即可
CG FG
求BG的长.
【详解】如图所示，连接GC ,
因为ABC为等腰三角形，AB AC，
第13页/共22页
学科网（北京）股份有限公司且以AB为直径的圆交BC于D，
所以ADBC，即D为BC的中点，
所以GCDGBD，BGCG，
又因为ACDABD，
所以ACGABG，
因为CE//AB，
所以CEGABG，
即CEG ACG FCG，
所以VEGC相似于△CGF ，
EG CG
即  CG2  EGFG，
CG FG
又因为EF 5,FG4，
所以CG2  EGFG(EFFG)FG36，
所以BGCG6.
故答案为：6.
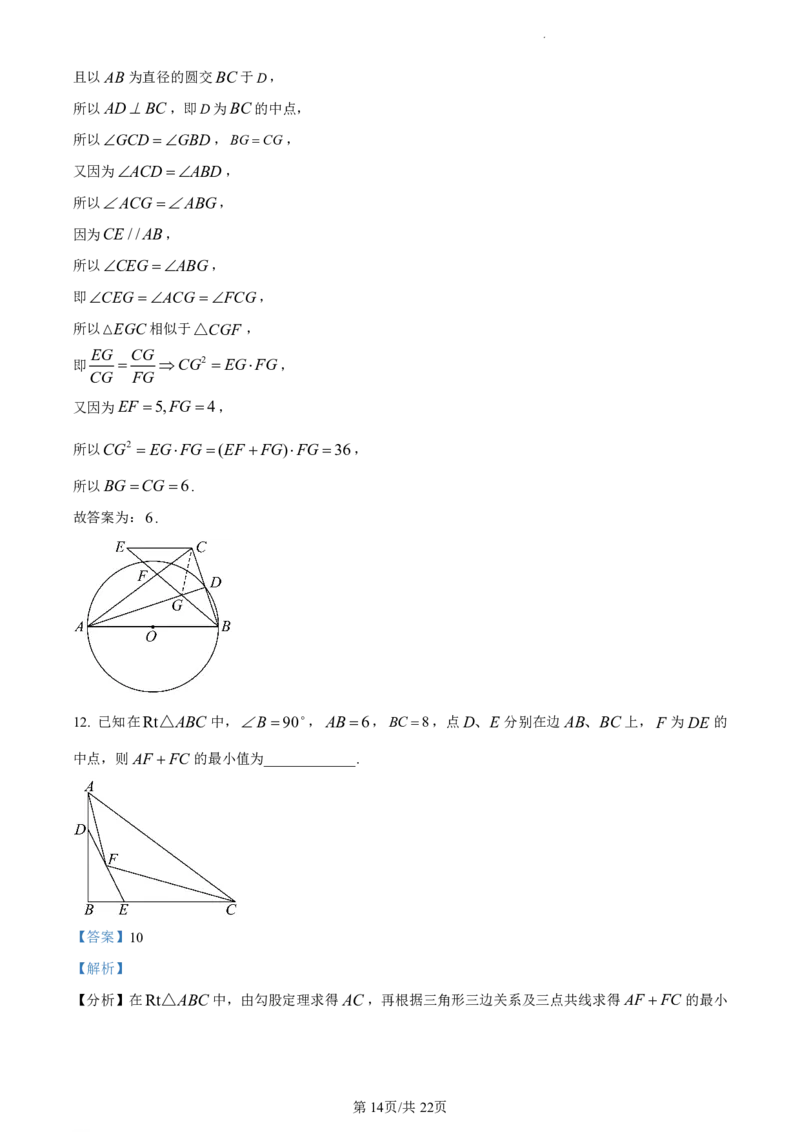
12. 已知在Rt△ABC 中，B 90，AB6，BC8，点D、E 分别在边 AB、BC上，F 为DE 的
中点，则AF FC 的最小值为_____________.
【答案】10
【解析】
【分析】在Rt△ABC中，由勾股定理求得AC，再根据三角形三边关系及三点共线求得AF FC 的最小
第14页/共22页
学科网（北京）股份有限公司值.
【详解】在Rt△ABC中，AC  62 82 10，
当A、F、C 三点不共线时，在△AFC中，AF FC  AC；
当A、F、C 三点共线时，AF FC  AC，
此时D与A重合，E与C重合，F 为AC的中点.
所以AF FC 的最小值为AC 10.
故答案为：10.
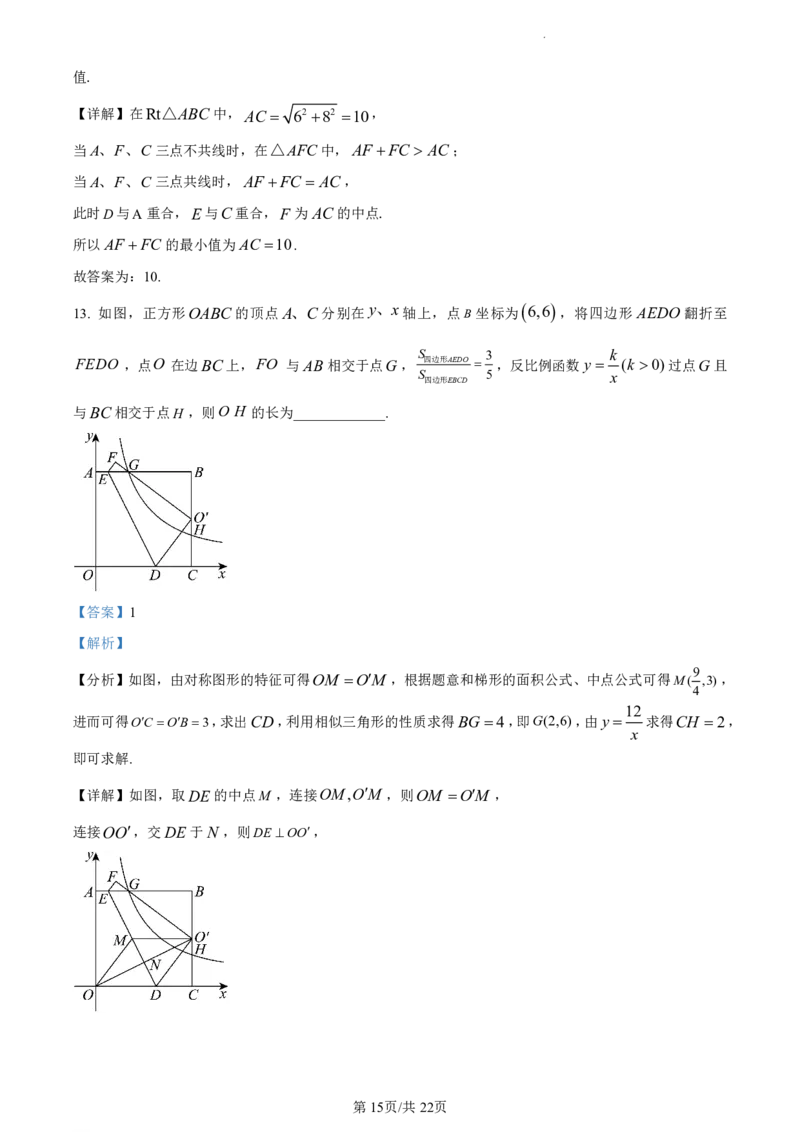
13. 如图，正方形OABC的顶点 A、C分别在 y、x轴上，点B坐标为  6,6  ，将四边形 AEDO 翻折至
S 3 k
FEDO ，点O 在边BC上，FO 与AB相交于点G， 四边形AEDO  ，反比例函数 y  (k 0)过点G且
S 5 x
四边形EBCD

与BC相交于点H ，则O H 的长为_____________.

 
【答案】1
【解析】
9
【分析】如图，由对称图形的特征可得OM OM ，根据题意和梯形的面积公式、中点公式可得M( ,3)，
4
12
进而可得OC OB3，求出CD，利用相似三角形的性质求得BG4，即G(2,6)，由y  求得CH 2，
x
即可求解.
【详解】如图，取DE的中点M ，连接OM,OM ，则OM OM ，
连接OO，交DE于N ，则DE OO，
第15页/共22页
学科网（北京）股份有限公司设AE a(0a6),ODb(0b6) ，则ODb,CD6b，
因为 S 四边形AEDO  3 ，所以S  3 36 27 ，即 1 6(ab) 27 ，
S 5 四边形AEDO 8 2 2 2
四边形EBCD
9 ab 9 9 15
解得ab ，所以M( ,3)( ,3)，则OM  ( )232  ，
2 2 4 4 4
9 15
设O(6,c)(0c6)，则OM  (6 )2(c3)2  ，解得c3，
4 4
即O(6,3)为CB的中点，故OC OB3.
 
又OM //DO，所以OM //OD,OM //OD，所以四边形OMOD为平行四边形，
15 9
则ODbOM  ，所以CD .
4 4
3 BG
OB BG 
由OBGDCO，得  ，即 9 3 ，解得BG4，
DC CO
4
k
所以AG6BG2，得G(2,6)，而点G在函数 y  图象上，
x
12
故k 12，则 y  ，所以H(6,2)，即CH 2，
x
所以OH OCCH 1.
故答案为：1
【点睛】关键点点睛：解决本题的关键是利用面积之比和中点坐标公式求出点M的坐标，进而求得O的坐
标，结合相似三角形的性质可得CH 2即为所求.
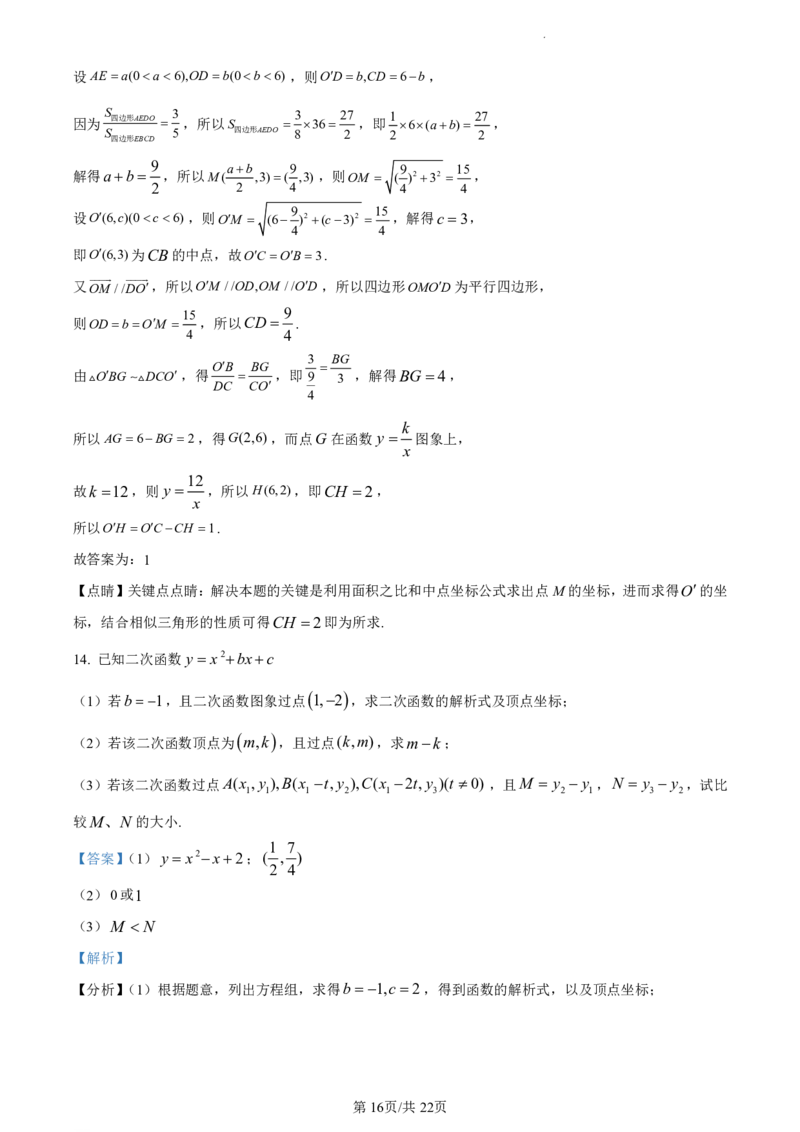
14. 已知二次函数 y  x2bxc
（1）若b= -1，且二次函数图象过点  1,2  ，求二次函数的解析式及顶点坐标；
 
（2）若该二次函数顶点为 m,k ，且过点(k,m)，求mk；
（3）若该二次函数过点A(x ,y ),B(x t,y ),C(x 2t,y )(t 0) ，且M  y y ，N  y  y ，试比
1 1 1 2 1 3 2 1 3 2
较M、N 的大小.
1 7
【答案】（1） y  x2x2；( , )
2 4
（2）0或1
（3）M  N
【解析】
【分析】（1）根据题意，列出方程组，求得b 1,c 2，得到函数的解析式，以及顶点坐标；
第16页/共22页
学科网（北京）股份有限公司（2）根据题意，可设抛物线的解析式为 y (xm)2k ，代入点(k,m)，得到关于mk的方程，即可求
解；
（3）根据题意，结合函数的解析式，求得 y  x2 bx c， y  x2 2xtt2 bx btc和
1 1 1 2 1 1 1
y  x2 4xt4t2 bx 2btc，求得M,N的表达式，利用作差比较法，即可求解.
3 1 1 1
【小问1详解】
由题意知：b= -1，且二次函数图象过点  1,2  ，
b1
可得 ，解得b 1,c 2，
1bc2
1 7
所以该函数的解析式为 y  x2x2，且函数图象的顶点坐标为( , ).
2 4
【小问2详解】
因为函数 y  x2bxc 中，二次项系数为1，
因为该函数图象的顶点坐标为  m,k  ，可设抛物线的解析式为 y (xm)2k ，
又因为 y (xm)2k 的图象进过另一点(k,m)，
可得m(km)2k，即mk (km)2，解得mk 0或mk 1.
【小问3详解】
因为函数 y  x2bxc 的图象经过点A(x ,y ),B(x t,y ),C(x 2t,y ) 三个不同点，
1 1 1 2 1 3
所以 y  x2 bx c，y (x t)2 b(x t)c x2 2xtt2 bx btc，
1 1 1 2 1 1 1 1 1
y (x 2t)2 b(x 2t)c x2 4xt4t2 bx 2btc，
3 1 1 1 1 1
所以M  y  y  x2 2xtt2 bx btc(x2 bx c)2xtt2 bt，
2 1 1 1 1 1 1 1
N  y  y  x2 4xt4t2 bx 2btc(x2 2xtt2 bx btc) 2xt3t2bt，
3 2 1 1 1 1 1 1 1
因为t 0，可得N M 2xt3t2 bt(2xtt2 bt)2t2 0，
1 1
所以M  N .
k
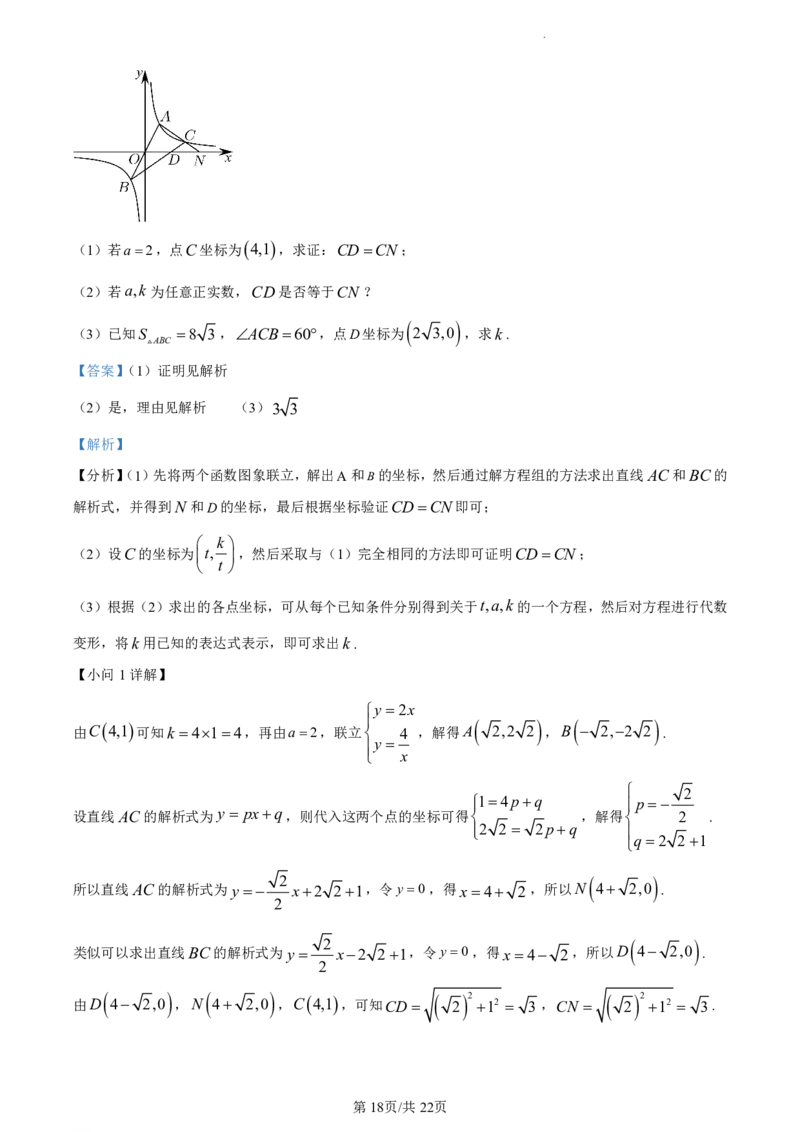
15. 如图，一次函数 yax  a0  与反比例函数 y   k 0 相交于A,B两点，点A在第一象限，点C是
x
k
反比例函数 y  第一象限上异于点A的一点，AC与x轴交于点N ，BC与x轴交于点D.
x
第17页/共22页
学科网（北京）股份有限公司 
（1）若a2，点C坐标为 4,1 ，求证：CDCN；
（2）若a,k 为任意正实数，CD是否等于CN ？
 
（3）已知S 8 3 ，ACB60，点D坐标为 2 3,0 ，求k.
ABC
【答案】（1）证明见解析
（2）是，理由见解析 （3）3 3
【解析】
【分析】（1）先将两个函数图象联立，解出A和B的坐标，然后通过解方程组的方法求出直线AC和BC的
解析式，并得到N 和D的坐标，最后根据坐标验证CDCN即可；
 k 
（2）设C的坐标为t, ，然后采取与（1）完全相同的方法即可证明CDCN；
 t 
（3）根据（2）求出的各点坐标，可从每个已知条件分别得到关于t,a,k的一个方程，然后对方程进行代数
变形，将k用已知的表达式表示，即可求出k.
【小问1详解】
y 2x
由C  4,1  可知k 414，再由a2，联立   4 ，解得A  2,2 2  ，B   2,2 2  .
y 
 x
 2
14pq p 
设直线AC的解析式为 y  pxq，则代入这两个点的坐标可得 ，解得 2 .
2 2  2pq 
q 2 21
2  
所以直线AC的解析式为 y x2 21，令 y0，得x4 2 ，所以N 4 2,0 .
2
2  
类似可以求出直线BC的解析式为y x2 21，令y0，得x4 2，所以D 4 2,0 .
2
由D  4 2,0  ，N  4 2,0  ，C  4,1  ，可知CD   2 2 12  3 ，CN   2 2 12  3.
第18页/共22页
学科网（北京）股份有限公司所以CDCN.
【小问2详解】
y ax
 k    k   k 
设Ct,   t 0  ，联立 k ，解得A  , ak   ，B   , ak   .
 t  y   a   a 
 x
k  ak

tpq
p 
t 
设直线AC的解析式为 y  pxq，则代入这两个点的坐标可得 ，解得 t .
 k  k
ak  pq q  ak 
  a  t
ak k k  k 
所以直线AC的解析式为 y x ak  ，令 y0，得xt ，所以N  t ,0  .
t t a  a 
ak k k  k 
类似可以求出直线BC的解析式为y x ak  ，令y0，得xt ，所以D  t ,0  .
t t a  a 
 k   k   k   k  2 k  2 k k2
由D   t a ,0   ，N   t a ,0   ，C  t, t   ，可知CD     a       t    a  t2 ，
 k  2 k  2 k k2
CN     a       t    a  t2 .
所以CDCN.
【小问3详解】
由于CDCN，故CDN CND.
而CDN CND ACB 60，故CDN CND 30.
 k   k   k   k   k 
之前已经求得A

, ak 

，B

 , ak 

，Ct, ，N

t ,0

，D

t ,0

.
 a   a   t   a   a 
  k
现在由已知有D 2 3,0 ，故t 2 3.
a
k
3 y t ak
同时我们有  tan30 tanCDN  C   .
3 x x k t
C D tt
a
1 1 3
而8 3 S  ACBCsinACB ACBCsin60 ACBC，故ACBC 32.
ABC 2 2 4
第19页/共22页
学科网（北京）股份有限公司  k  2 k  2  k  2 k  2
所以1024322  AC2BC2    t      ak     t      ak  
  a   t   a   t  
 
 2 2 2 2
 k  ak  k   k  ak  k 
 t    t  t    t 
  a  t2  a   a  t2  a  
       
 
2
 ak  2 k  2  k  2   ak  2  k  2  k  2
   1 t2      t a       t a      1   t         t a       t a    .
 
2
 2 2 2
k ak 3  ak   k   k 
故我们最终得到：t 2 3，  ，1   t  t  1024 .
     
a t 3   t    a   a 
 
2 2
 2 2 2  2 2 2
 ak   k   k   3  2  k  64 k 
从而10241   t  t  1   2 3 t   t  ，
           
  t    a   a    3    a  3  a 
   
2
 k  k
得t   48，即t 4 3.
 
 a  a
所以有
 2 2
 k  ak 1  k   k  ak 1 2  2 3
k t    t  t     4 3  2 3  3 3.
     
a t 4 a a  t 4  3
     
 
综上，k的值为3 3.
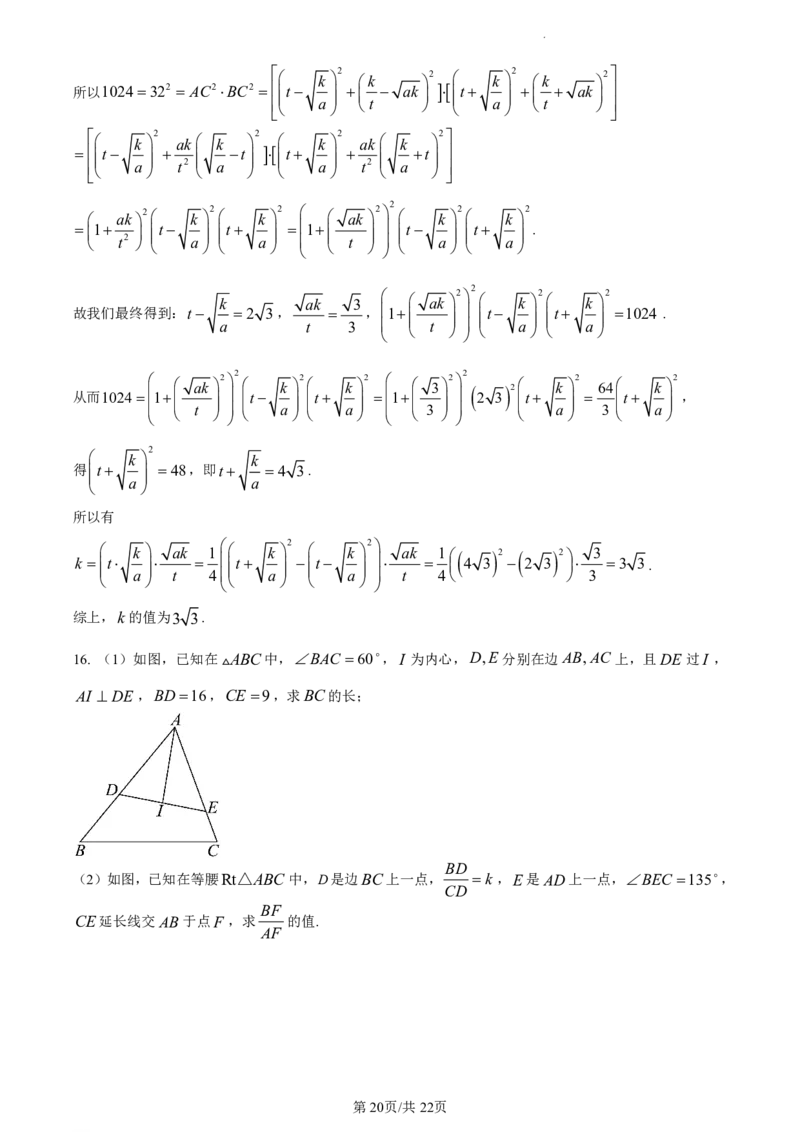
16. （1）如图，已知在ABC中，BAC 60，I 为内心，D,E分别在边AB,AC上，且DE 过I ，
AI  DE，BD 16，CE 9，求BC的长；
BD
（2）如图，已知在等腰Rt△ABC中，D是边BC上一点， k ，E是AD上一点，BEC 135，
CD
BF
CE延长线交 AB于点F ，求 的值.
AF
第20页/共22页
学科网（北京）股份有限公司【答案】（1）37；（2） 2k
【解析】
【分析】（1）过点I 分别作AB,BC,CA的垂线，记垂足为H,F,G.设DH  x，用两种方法表示出三角形
ABC的面积从而建立方程即可求解；
（2）作出ABC的外接圆，记CF 与外接圆交于点G,BE与AC交于点H ，与外接圆交于点P.结合相似
三角形的性质以及赛瓦定理即可得解.
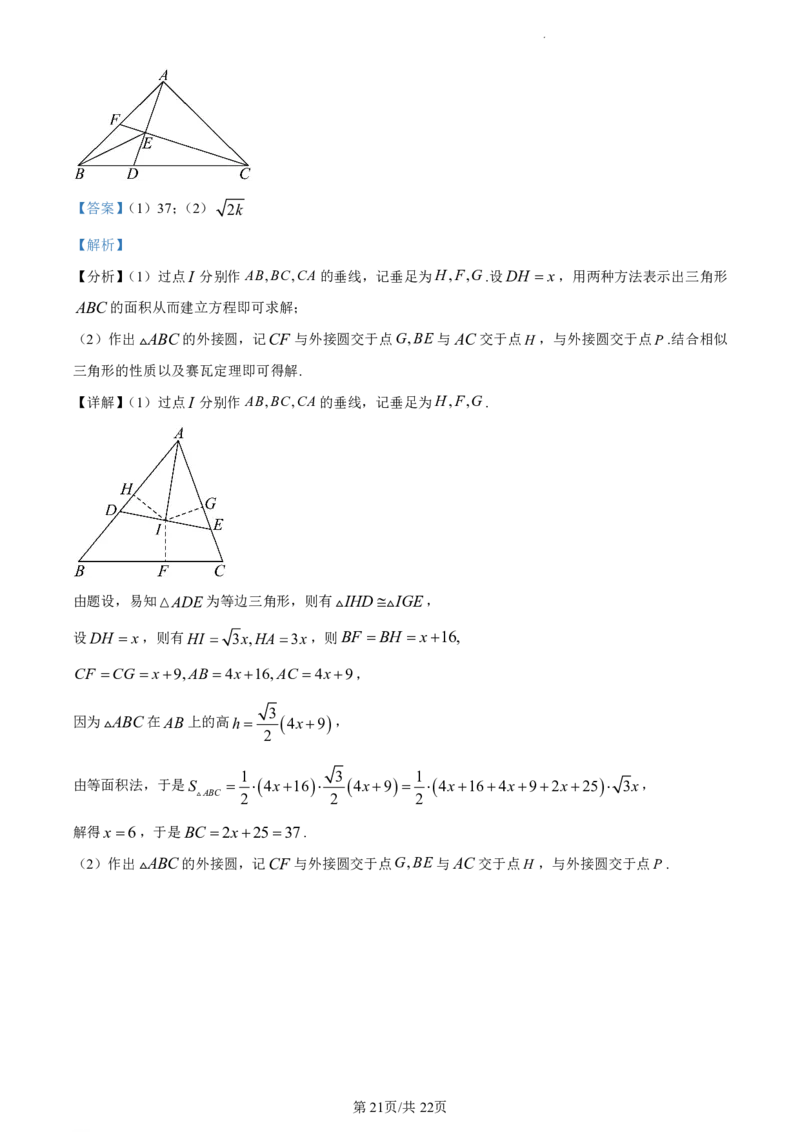
【详解】（1）过点I 分别作AB,BC,CA的垂线，记垂足为H,F,G.
由题设，易知VADE为等边三角形，则有IHDIGE，
设DH  x，则有HI  3x,HA3x，则BF  BH  x16,
CF CG  x9,AB 4x16,AC 4x9，
3
因为ABC在AB上的高h  4x9 ，
2
1 3 1
由等面积法，于是S   4x16   4x9   4x164x92x25  3x，
ABC 2 2 2
解得x6，于是BC 2x2537.
（2）作出ABC的外接圆，记CF 与外接圆交于点G,BE与AC交于点H ，与外接圆交于点P.
第21页/共22页
学科网（北京）股份有限公司因为AGC ABC  45,APB ACB  45，结合BEC PEG135，
显然APEG为平行四边形，于是AG//BP,AP//GC，
所以PAC ACG，GABABP，
结合同圆中圆周角相等，对应弧、弦相等，则AG  PC，APGB，
由上，GABGCB，GBAEBC，进而有BAG BCE，
由题意，易知BC为直径，且
G

P A

C
，则BPC 90，AGC PCG45，
同理有BGC 90，GBC PCG45，
2
所以CE  2PC  2AG，BG  BE，
2
CH CE 2AG 2AG AF
    2
由AHP~CHE且AFG~BFE，所以 HA AP BG 2 BF .
BE
2
BD CH AF AF AF BF
  1 k2  1  2k
由赛瓦定理有 DC HA FB ，即 BF FB ，因此 AF .
第22页/共22页
学科网（北京）股份有限公司