文档内容
9月月考答案
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求
的。
1.已知命题p:∀x∈R,−x2 +4x+3>0,则命题p的否定为( )
A. ∀x∈R,−x2 +4x+30 B. ∀x∈R,−x2 +4x+3<0
C. ∃x∈R,−x2 +4x+30 D. ∃x∈R,−x2 +4x+3<0
【答案】C
2.下列各组函数是同一函数的是( )
x
A. y = 与y =1 B. y = (x−1)2 与y=x−1
x
x2 x3+x
C. y = 与y = x D. y = 与y = x
x x2 +1
【答案】D
b
3. “a>b”是“ <1”的( )
a
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】D
b
【解析】a>0时,由 <1,解得:a>b,a<0时,解得:ab也推不出 <1,比如a=0,b=−1,不是充分条件,
a
b
故“a>b”是“ <1”的既不充分也不必要条件.
a
故选:D.
4. 若a>b,d >c,且 , ,则( )
A. bb, ,所以ba或d c,所以d a,
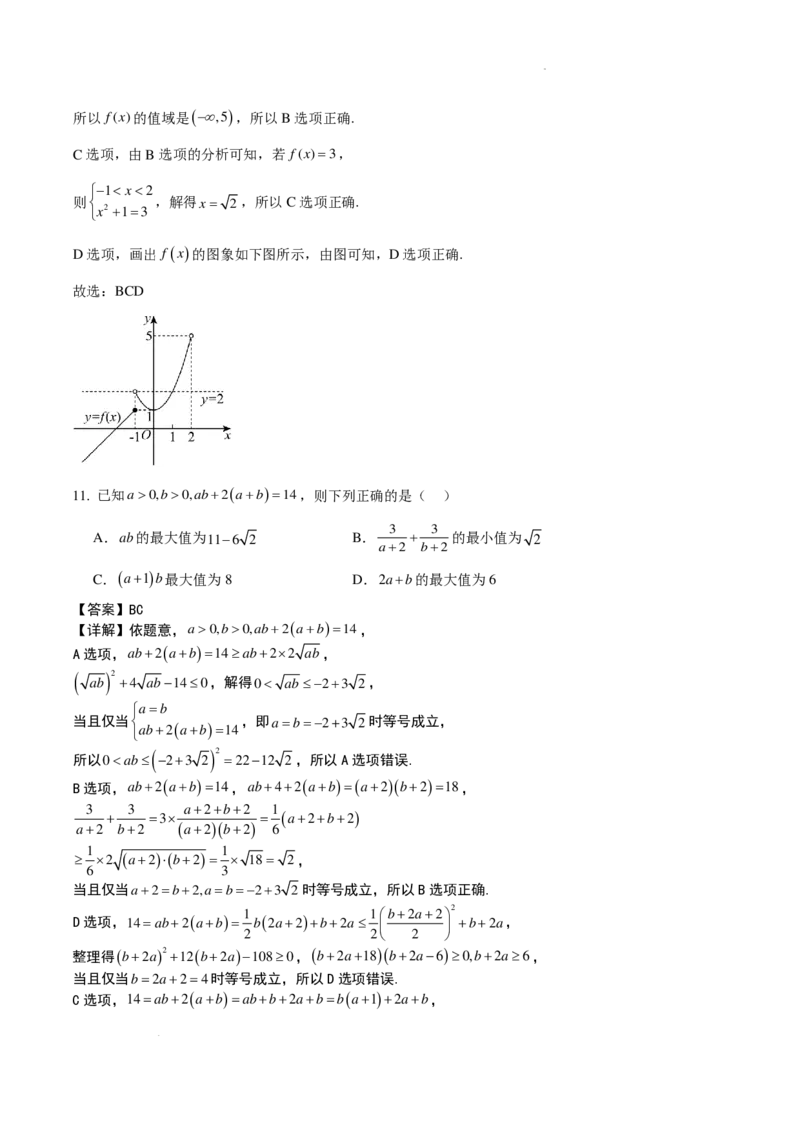
学科网(北京)股份有限公司综上:b0的解集为 x −2< x<1 ,则函数 y=ax2 −bx+c的图象大致为( )
A. B.
C. D.
【答案】A
{ }
【详解】因为ax2 −bx+c>0的解集为 x −2< x<1 ,
所以方程ax2 −bx+c=0的两根分别为−2和1,且a<0,
b
−2+1= ,
a b=−a,
则 变形可得
(−2 )×1=
c
,
c=−2a,
a
故函数y =ax2 −bx+c=ax2 +ax−2a=a ( x+2 )( x−1 ) 的图象开口向下,
学科网(北京)股份有限公司且与x轴的交点坐标为 ( 1,0 ) 和 (−2,0 ) ,故A选项的图象符合.
故选:A
7. 关于x的不等式x2−(1+2a)x+2a<0的解集中恰有2个整数,则实数a的取值范围是( )
A. { a −2≤a<−1或3 时,原不等式解得10,b>0,ab+2(a+b)=14,则下列正确的是( )
3 3
A.ab的最大值为11−6 2 B. + 的最小值为 2
a+2 b+2
C.(a+1)b最大值为8 D.2a+b的最大值为6
【答案】BC
【详解】依题意,a>0,b>0,ab+2(a+b)=14,
A选项,ab+2(a+b)=14≥ab+2×2 ab,
( )2
ab +4 ab−14≤0,解得0< ab ≤−2+3 2,
a=b
当且仅当
ab+2(a+b)=14
,即a=b=−2+3 2时等号成立,
( )2
所以01},B={x|x>a},若A⊆B,则实数a的取值范围是______.
【答案】(−∞,1]
1
13. 函数 f(x)= + 1−x 的定义域是_________.
x
【答案】
(−∞,0 )∪(
0,1
]
1
14. .定义集合P={x|a≤x≤b}的“长度”是b−a,其中a,b∈R.已如集合M ={x|m≤x≤m+ },
2
3
N ={x|n− ≤x≤n},且M,N都是集合{x|1≤x≤2}的子集,则集合M ∩N 的“长度”的最小值是 ;
5
6 3
若m= ,集合M ∪N 的“长度”大于 ,则n的取值范围是 .
5 5
1 8 17 9
【答案】 /0.1
, ∪ ,2
10 5 10 5
1 3
【详解】集合M ={x|m≤x≤m+ },N ={x|n− ≤x≤n},且M,N都是集合{x|1≤x≤2}的子集,
2 5
m≥1 3
3 n− ≥1 8
由 1 ,可得1≤m≤ ,由 5 ,可得 ≤n≤2.
m+ 2 ≤2 2 n≤2 5
要使M ∩N 的“长度”最小,只有当m取最小值、n取最大或m取最大、n取最小时才成立.
7 3 3 7 1
当m=1,n=2,M ∩N =x ≤x≤ ,“长度”为 − = ,
5 2 2 5 10
3 8 3 8 8 3 1
当m= ,n= ,M ∩N =x ≤x≤ ,“长度”为 − = ,
2 5 2 5 5 2 10
1
故集合M ∩N 的“长度”的最小值是 ;
10
6 6 17
若m= ,M =x ≤x≤ ,
5 5 10
3 3 17 3 6 3
要使集合M ∪N 的“长度”大于 ,故n− < − 或n> + ,
5 5 10 5 5 5
17 9 8 8 17 9
即n< 或n> ,又 ≤n≤2,故n∈ , ∪ ,2 .
10 5 5 5 10 5
1 8 17 9
故答案为: ; , ∪ ,2 .
10 5 10 5
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
2x−1 { }
15. (13分)已知R为全集,集合A=x| ≤1,x∈R,集合B= x a−1≤ x≤a+1 .
x+1
(1)求集合A;
学科网(北京)股份有限公司(2)若B∩C Α= B,求实数a的取值范围.
R
【答案】(1)A={ x −12}
因为 B∩A=B ,所以B⊆ A,
{ }
又B= x a−1≤ x≤a+1 ,
因为a−12,
解得:a≤−2或a>3,
综上:实数a的取值范围为(−∞,−2 ](3,+∞)
.
16.(15分)已知集合A= { x x2−5x−6<0 } ,B={ x m+1m+1⇒m>2
命题p:∃x∈A,x∈B是真命题,可知AB≠∅,
因为A={x|−12
,∴2m+1
7
m+1≥−1 ,解得20, 且a+2b+3c=4.
(2b+3c)2 (a+3c)2 (a+2b)2
(1)证明: + + ≥8.
a+2b 2b+3c a+3c
1 1 a
(2)若2b=3c, 求 − + 的最小值.
2a+1 2b+3 3c+3
(2b+3c)2 (2b+3c)2
【详解】(1) +a+2b≥2 ⋅(a+2b) =2(2b+3c),①
a+2b a+2b
(a+3c)2 (a+3c)2
+2b+3c≥2 ⋅(2b+3c) =2(a+3c)②
2b+3c 2b+3c
(a+2b)2 (a+2b)2
+a+3c≥2 ⋅(a+3c) =2(a+2b)③
a+3c a+3c
(2b+3c)2 (a+3c)2 (a+2b)2
①+②+③得 + + +2(a+2b+3c)≥4(a+2b+3c),
a+2b 2b+3c a+3c
(2b+3c)2 (a+3c)2 (a+2b)2
即 + + ≥2(a+2b+3c)=8,
a+2b 2b+3c a+3c
4
当且仅当a=2b=3c= 时,等号成立.
3
(2)由2b=3c,得a+4b=4,即a=4−4b,
1 1 a 1 1 4−4b 1 1 −4b−6+10
所以 − + = − + = − +
2a+1 2b+3 3c+3 2a+1 2b+3 2b+3 2a+1 2b+3 2b+3
1 9
= + −2
2a+1 2b+3
1
由a+4b=4,得2a+8b=8,得(2a+1)+4(2b+3)=21,即
(2a+1)+4(2b+3)
=1,
21
1 9 1 1 9 1 4(2b+3) 9(2a+1)
所以 + = + (2a+1)+4(2b+3) = 37+ +
2a+1 2b+3 212a+1 2b+3 21 2a+1 2b+3
1
4(2b+3) 9(2a+1)
7
≥ [37+2 ⋅ = .
21 2a+1 2b+3 3
学科网(北京)股份有限公司1 1 a 7 1
所以 − + 的最小值为 −2= ,
2a+1 2b+3 3c+3 3 3
4(2b+3) 9(2a+1) 3
当且仅当 = ,即a=1,b= 时,等号成立.
2a+1 2b+3 4
18. (17分)LED灯具有节能环保的作用,且使用寿命长.经过市场调查,可知生产某种LED灯需投入的
年固定成本为4万元,每生产x万件该产品,需另投入变动成本W(x)万元,在年产量不足6万件时,
1 100
W(x)= x2 +x,在年产量不小于6万件时,W(x)=7x+ −39.每件产品售价为6元.假设该产品每年
2 x
的销量等于当年的产量.
(1)写出年利润L(x)(万元)关于年产量x(万件)的函数解析式.(注:年利润=年销售收入-固定成本-变动
成本)
(2)年产量为多少万件时,年利润最大?最大年利润是多少?
【答案】解:(1)每件产品售价为6元,∴x万件产品的销售收入为6x万元,
1 1
依题意得,当0< x<6时,L(x)=6x− x2 +x−4=− x2 +5x−4,
2 2
当x6时,
1 17
(2)当0< x<6时,L(x)=− (x−5)2 + ,
2 2
17
当x=5时,L(x)取得最大值 .
2
100 100
当x6时,L(x)=35−x+ 35−2 x⋅ =35−20=15,
x x
100
当且仅当x= ,即x=10时,L(x)取得最大值15.
x
,
∴当年产量为10万件时,年利润最大,最大年利润为15万元.
1 2 1 2 1 2 b
19. 问题:正实数a,b满足a+b=1,求 + 的最小值.其中一种解法是: + = + (a+b)=1+
a b a b a b a
2a b 2a
+ +2≥3+2 2,当且仅当 = 且a+b=1时,即a= 2−1且b=2− 2时取等号.学习上述解法并解
b a b
决下列问题:
学科网(北京)股份有限公司2 3
(1)若正实数x,y满足x+y=1,求 + 的最小值;
x y
x2 y2
(2)若实数a,b,x,y满足 − =1,求证:a2−b2 ≤(x−y)2;
a2 b2
(3)求代数式M = 3m−5− m−2的最小值,并求出使得M最小的m的值. 【分析】(1)利用“1”的代换
凑配出积为定值,从而求得和的最小值;
x2 y2 b2x2 a2y2
(2)利用已知,a2−b2 =(a2−b2)×1=(a2−b2)( − )=x2+y2−( + ),然后由基本不等式进行
a2 b2 a2 b2
b2x2 a2y2
放缩: + ≥2 xy ,再利用不等式的性质得出大小.并得出等号成立的条件.
a2 b2
x2 y2
x2 y2 − =1
(3)令x= 3m−5,y= m−2,构造 − =1,即以x2−3y2 =1,即 1 1 ,然后利用(2)的
a2 b2
3
结论可得.
【详解】(1)因为x>0,y>0,x+y=1,
2 3 2 3 3x 2y 3x 2y
所以 + =(x+y)( + )=5+ + ≥5+2 × =5+2 6,
x y x y y x y x
3x 2y
当且仅当 = ,即x= 6−2,y=3− 6时取等号,
y x
所以x+y的最小值是5+2 6.
x2 y2 b2x2 a2y2
(2)a2−b2 =(a2−b2)×1=(a2−b2)( − )=x2+y2−( + ),
a2 b2 a2 b2
b2x2 a2y2 b2x2 a2y2 b2x2 a2y2
又 + ≥2 ⋅ =2 xy ,当且仅当 = 时等号成立,
a2 b2 a2 b2 a2 b2
b2x2 a2y2
所以x2+y2−( + ) ≤x2+y2−2 xy ≤x2+y2−2xy=(x−y)2,
a2 b2
b2x2 a2y2 x2 y2
所以a2−b2 ≤(x−y)2,当且仅当 = 且x,y同号时等号成立.此时x,y满足 − =1.
a2 b2 a2 b2
3m−5≥0
(3)令x= 3m−5,y= m−2,由 得m≥2,
m−2≥0
x2−y2 =(3m−5)−(m−2)=2m−3>0,
又x>0,y>0,所以x> y,
x2 y2
构造 − =1,
a2 b2
学科网(北京)股份有限公司x2 y2
− =1 1
由x2−3y2 =1,可得 1 1 ,因此a2 =1,b2 = ,
3
3
1 6
由(2)知M = 3m−5− m−2 =x−y≥ a2−b2 = 1− = ,
3 3
1
取等号时, x2 =3y2且x,y同正,
3
6 6 6 13
结合x2−3y2 =1,解得x= ,y= ,即 3m−5= ,m= .
2 6 2 6
13 6
所以m= 时,M 取得最小值 .
6 3
b2
2−1
综上:
4
( a2+c2) 的最大值为
2
.
学科网(北京)股份有限公司