文档内容
第2单元 一元二次函数、方程与不等式(强化篇)
基础知识讲解
一.不等式定理
【基础知识】
①对任意的a,b,有a>b⇔a﹣b>0;a=b⇒a﹣b=0;a<b⇔a﹣b<0,这三条性质是做差
比较法的依据.
②如果a>b,那么b<a;如果a<b,那么b>a.
③如果a>b,且b>c,那么a>c;如果a>b,那么a+c>b+c.
推论:如果a>b,且c>d,那么a+c>b+d.
④如果a>b,且c>0,那么ac>bc;如果c<0,那么ac<bc.
二.不等式大小比较
【技巧方法】
不等式大小比较的常用方法
(1)作差:作差后通过分解因式、配方等手段判断差的符号得出结果;
(2)作商(常用于分数指数幂的代数式);
(3)分析法;
(4)平方法;
(5)分子(或分母)有理化;
(6)利用函数的单调性;
(7)寻找中间量或放缩法;(8)图象法.其中比较法(作差、作商)是最基本的方法.
三.基本不等式
【基础知识】
基本不等式主要应用于求某些函数的最值及证明不等式.其可表述为:两个正实数的几
何平均数小于或等于它们的算术平均数.公式为: ≥ (a≥0,b≥0),变形为ab≤
( )2或者a+b≥2 .常常用于求最值和值域.
四、基本不等式的应用
【基础知识】
1、求最值
2、利用基本不等式证明不等式
3、基本不等式与恒成立问题
4、均值定理在比较大小中的应用
【技巧方法】
技巧一:凑项
需要调整项的符号,又要配凑项的系数,使其积为定值.
技巧二:凑系数
遇到无法直接运用基本不等式求解,但凑系数后可得到和为定值,从而可利用基本不等式
求最大值.
技巧三:分离
技巧四:换元
一般,令t=x+1,化简原式在分离求最值.技巧五:结合函数f(x)=x+ 的单调性.
技巧六:整体代换
多次连用最值定理求最值时,要注意取等号的条件的一致性,否则就会出错.
技巧七:取平方
两边平方构造出“和为定值”,为利用基本不等式创造条件.
总结我们利用基本不等式求最值时,一定要注意“一正二定三相等”,同时还要注意一些
变形技巧,积极创造条件利用基本不等式.
五.二次函数的性质
【基础知识】
二次函数相对于一次函数而言,顾名思义就知道它的次数为二次,且仅有一个自变量,因
变量随着自变量的变化而变化.它的一般表达式为:y=ax2+bx+c(a≠0)
【技巧方法】
①开口、对称轴、最值与x轴交点个数,当a>0(<0)时,图象开口向上(向下);对称
轴x= ;最值为:f( );判别式△=b2﹣4ac,当△=0时,函数与x轴只有一
个交点;△>0时,与x轴有两个交点;当△<0时无交点.
②根与系数的关系.若△≥0,且x 、x 为方程y=ax2+bx+c的两根,则有x +x = ,
1 2 1 2
x •x = ;
1 2③二次函数其实也就是抛物线,所以x2=2py的焦点为(0, ),准线方程为y= ,
含义为抛物线上的点到到焦点的距离等于到准线的距离.
④平移:当y=a(x+b)2+c向右平移一个单位时,函数变成y=a(x﹣1+b)2+c;
六.一元二次不等式
【基础知识】
含有一个未知数且未知数的最高次数为2的不等式叫做一元二次不等式.它的一般形
式是 ax2+bx+c>0 或 ax2+bx+c<0(a不等于0)其中ax2+bx+c是实数域内的二次三项式.
【技巧方法】
(1) 当△=b2﹣4ac>0时,
一元二次方程ax2+bx+c=0有两个实根,那么ax2+bx+c可写成a(x﹣x )(x﹣x )
1 2
(2) 当△=b2﹣4ac=0时,
一元二次方程ax2+bx+c=0仅有一个实根,那么ax2+bx+c可写成a(x﹣x )2.
1
(3) 当△=b2﹣4ac<0时.
一元二次方程ax2+bx+c=0没有实根,那么ax2+bx+c与x轴没有交点.
二.不等式的解法
(1)整式不等式的解法(根轴法).
步骤:正化,求根,标轴,穿线(偶重根打结),定解.
特例:
①一元一次不等式ax>b 解的讨论;
②一元二次不等式ax2+bx+c>0(a≠0)解的讨论.
(2)分式不等式的解法:先移项通分标准化,.(3)无理不等式:转化为有理不等式求解.
(4)指数不等式:转化为代数不等式
(5)对数不等式:转化为代数不等式
(6)含绝对值不等式
①应用分类讨论思想去绝对值;
②应用数形思想;
③应用化归思想等价转化.
七.一元二次方程根与系数的关系
【基础知识】
一元二次方程根与系数的关系其实可以用一个式子来表达,即当ax2+bx+c=0(a≠0)
有解时,不妨设它的解为x ,x ,那么这个方程可以写成ax2﹣a(x +x )x+ax •x =0.即
1 2 1 2 1 2
x2﹣(x +x )x+x •x =0.它表示根与系数有如下关系:x +x =﹣ ,x •x = .
1 2 1 2 1 2 1 2
习题演练
一.选择题(共12小题)
1.关于x的不等式 的解集为 ,且: ,则a=
( )
A. B. C. D.
2.已知a,b为非零实数,且 ,则下列命题成立的是( )A. B. C. D.
3.若 ,则下列不等式中一定成立的是( )
A. B.
C. D.
4.两个正实数 , 满足 , , 成等差数列,则不等式 恒成立时
实数 的取值范围是( )
A. B. C. D.
5.设 , , ,则 的最小值为( )
A. B. C. D.
6.已知 ,则 的最小值为( ).
A.9 B. C.5 D.
7.若 , , ,则 的最大值为( )A. B. C. D.
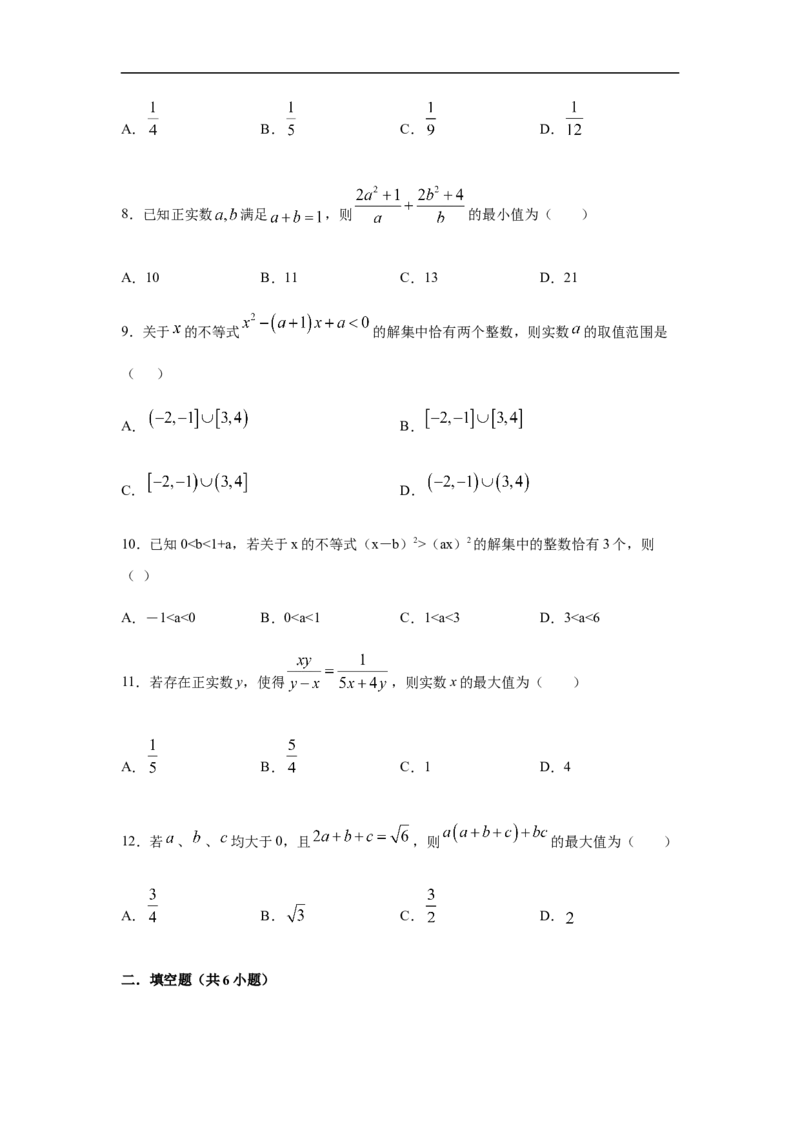
8.已知正实数 满足 ,则 的最小值为( )
A.10 B.11 C.13 D.21
9.关于 的不等式 的解集中恰有两个整数,则实数 的取值范围是
( )
A. B.
C. D.
10.已知0(ax)2的解集中的整数恰有3个,则
( )
A.-1