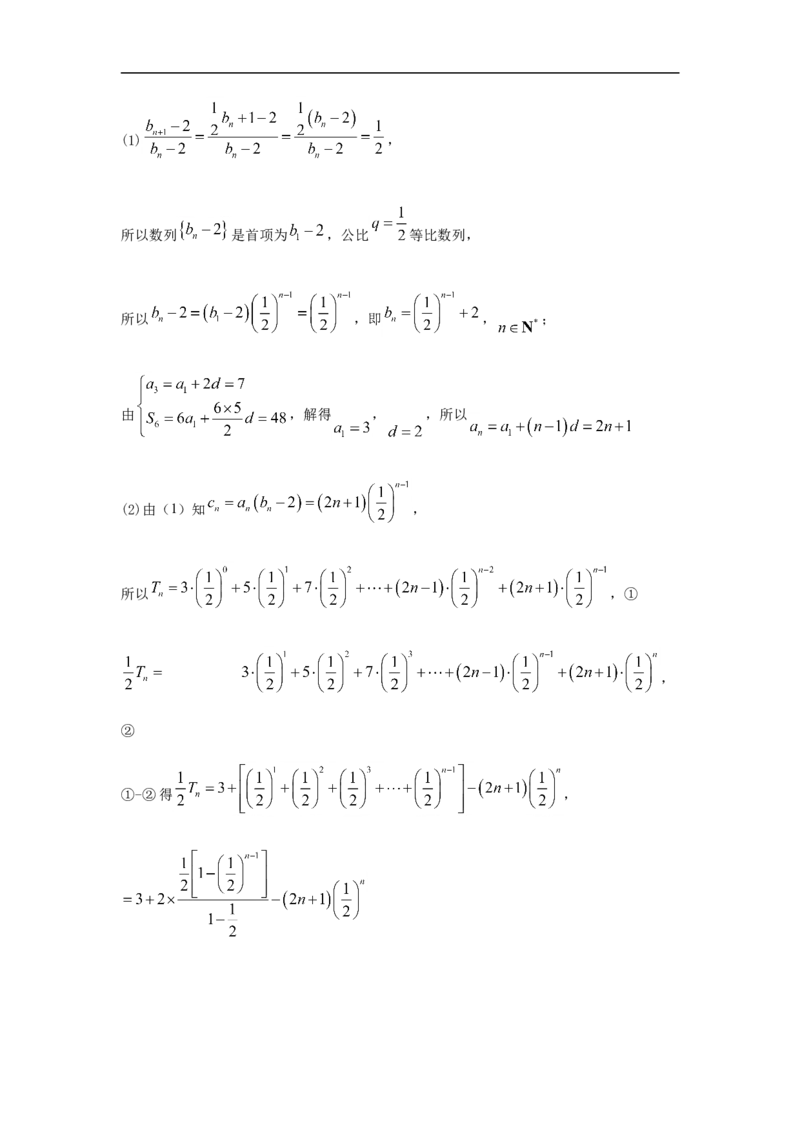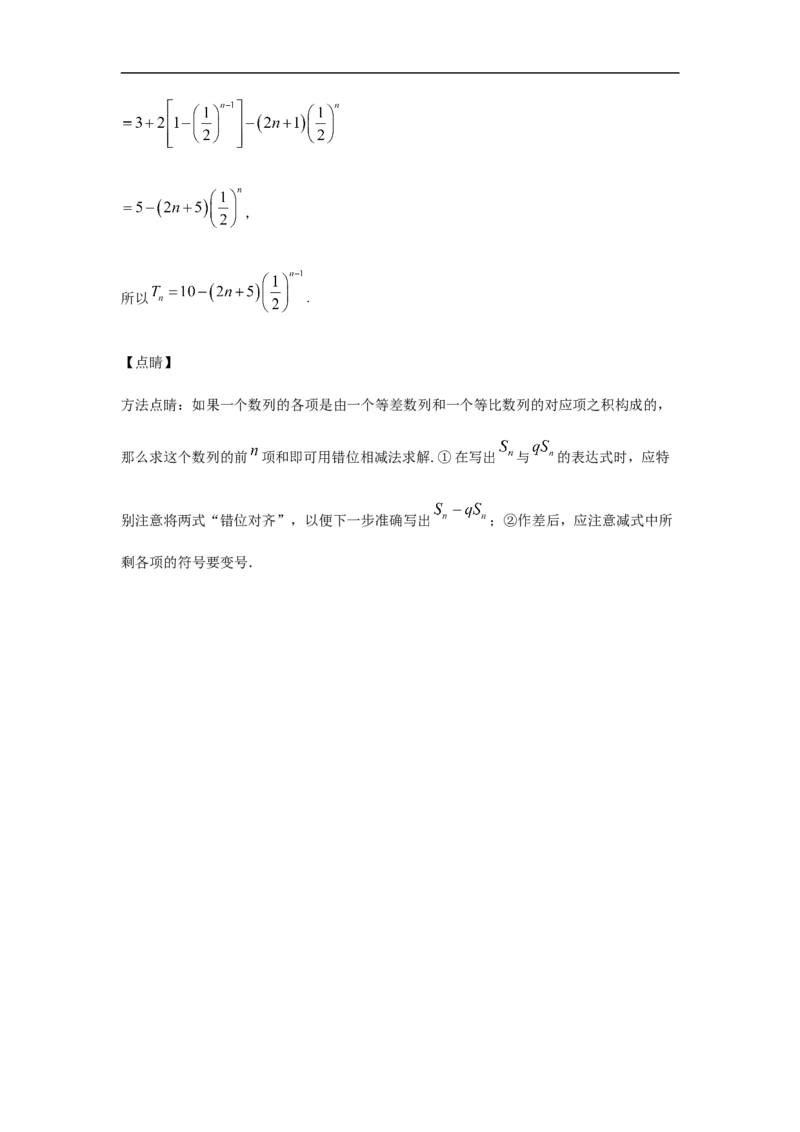文档内容
人教A版选择性必修第二册第四章数列综合测试2
一、单选题
1.设数列 满足 ,则 ( )
A.2 B.4 C.8 D.16
2.在等差数列 中, ,则 等于( ).
A.6 B.12 C.24 D.32
3.等比数列 中, , ,则 等于(
)
A.16 B.32 C.64 D.128
4.设数列 的通项公式为 ,要使它的前 项的乘积大于36,则 的最
小值为( )
A.6 B.7 C.8 D.9
5.在各项均为正数的等比数列 中, ,则 的最大值是(
)
A.25 B. C.5 D.
6.已知等差数列 的公差 为正数, 为常数,
则 ( )A. B. C. D.
7.在等差数列 中, , ,则 中最大的是( )
A. B. C. D.
8.设等差数列 、 的前 项和分别是 、 .若 ,则 的值为
( )
A. B. C.1 D.2
9.在数列 中, , ,则 (
)
A.10 B.145
C.300 D.320
10.《张丘建算经》卷上第 题为:“今有女善织,日益功疾(注:从第 天开始,
每天比前一天多织相同量的布),第一天织 尺布,现一月(按 天计)共织
尺”,则从第 天起每天比前一天多织( )
A. 尺布 B. 尺布 C. 尺布 D. 尺布
11.若一个数列的第m项等于这个数列的前m项的乘积,则称该数列为“m积列”.若各
项均为正数的等比数列{a}是一个“2022积数列”,且a>1,则当其前n项的乘积取最
n 1
大值时,n的最大值为( )
A.1009 B.1010 C.1011 D.202012.已知数列 的前 项和为 , , 且 ,满足
,数列 的前 项和为 ,则下列说法中错误的是( )
A. B.
C.数列 的最大项为 D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
13.在公差不为0的等差数列{a}中,a、a、a 成等比数列,则该等比数列的公比为
n 1 3 4
_______ .
14.若等差数列 和等比数列 满足 , ,则
_________.
15.在数列 中, , , ,记
,若对任意的 , 恒成立,则实数 的取值范围
为______.
16.有一个数阵排列如下:
1 2 4 7 11 16 22……3 5 8 12 17 23…………
6 9 13 18 24………………
10 14 19 25……………………
15 20 26…………………………
21 27………………………………
28……………………………………
………………………………………
则第40行从左至右第6个数字为______.
三、解答题
17.已知数列 的前n项和为 , , , , ,且当
时, .
(Ⅰ)求 的值;
(Ⅱ)证明: 为等比数列.
18.已知数列 的前 项和 与通项 满足 .
(1)求数列 的通项公式;
(2)设 , , ,
求 .19.已知数列 的前n项和为 .
(Ⅰ)若 为等差数列,求证: ;
(Ⅱ)若 ,求证: 为等差数列.
20.在数列 中, , .
(1)设 ,证明: 是等比数列,并求 的通项公式;
(2)设 为数列 的前n项和,证明: .
21.设等差数列 的前n项和为 , , ,数列 的前n
项和为 ,满足 .
(1)求数列 的通项公式及数列 的前n项和;
(2)判断数列 是否为等比数列,并说明理由.
22.已知等差数列 的前 项和为 , , ,数列 满足
, .
(1)证明:数列 是等比数列,并求数列 与数列 通项公式;
(2)若 ,求数列 的前 项和 .参考答案
1.D
【分析】
根据等比数列的定义可得数列 是以2为公比的等比数列,由此可得选项.
【详解】
因为数列 满足 ,所以数列 是以2为公比的等比数列,
所以 ,
故选:D.
【点睛】
本题考查等比数列的定义,属于基础题.
2.A
【分析】
由等差数列的性质可得选项.
【详解】
由等差数列的性质得 ,
故选:A.
【点睛】
本题考查等差数列的性质,属于基础题.
3.A【分析】
由 ,求得 ,再由 求解.
【详解】
, .
∴ ,
∴ .
故选:A
4.C
【分析】
先求出数列 的前 项的乘积为 ,令 解不等式,结合 ,即可求解.
【详解】
记数列 的前 项的乘积为 ,则
依题意有
整理得
解得: ,因为 ,所以 ,
故选:C
5.B
【分析】
由等比数列的性质,求得 ,再结合基本不等式,即可求得 的最大值,得到
答案.
【详解】
由等比数列的性质,可得 ,
又因为 ,所以 ,所以 ,
当且仅当 时取等号.
故选:B.
6.A
【分析】
由已知等式分别求出数列的前三项,由 列出方程,求出公差,利用等差数列
的通项公式求解可得答案.
【详解】
, ,
令 ,则 ,解得令 ,则 ,即 ,若 ,则 ,
与已知矛盾,故解得
等差数列, ,即 ,解得
则公差 ,所以 .
故选:A
7.B
【分析】
设等差数列的公差为d.由已知得 ,可得关系 .再运用
求和公式和二次函数的性质可得选项.
【详解】
设等差数列的公差为d.由 得, ,整理得, .
又 ,所以 ,因此 ,
所以 最大.
故选:B.
8.C
【分析】令 , ,求出 , ,进而求出 , ,则 可得.
【详解】
令 , ,
可得当 时, ,
,
当 , ,符合 ,
故 , ,
故 .
【点睛】
由 求 时, ,注意验证a 是否包含在后面a 的公式中,若不符
1 n
合要单独列出,一般已知条件含a 与S 的关系的数列题均可考虑上述公式求解.
n n
9.C
【分析】
由等差数列的性质可得 ,结合分组求和法即可得解。
【详解】因为 , ,
所以数列 是以 为首项,公差为3的等差数列,
所以 ,
所以当 时, ;当 时, ;
所以
.
故选:C.
10.D
【分析】
设该女子第 尺布,前 天工织布 尺,则数列 为等差数列,设其公
差为 ,根据 , 可求得 的值.
【详解】
设该女子第 尺布,前 天工织布 尺,则数列 为等差数列,设其公
差为 ,
由题意可得 ,解得 .
故选:D.11.C
【分析】
根据数列的新定义,得到 ,再由等比数列的性质得到 ,再利用
求解即可.
【详解】
根据题意: ,
所以 ,
因为{a}等比数列,设公比为 ,则 ,
n
所以 ,
因为 ,所以 ,
所以 ,
所以前n项的乘积取最大值时n的最大值为1011.
故选:C.
【点睛】
关键点睛:本题主要考查数列的新定义以及等比数列的性质,数列的最值问题,解题的关
键是根据定义和等比数列性质得出 以及 进行判断.
12.D
【分析】当 且 时,由 代入 可推导出数列 为等差
数列,确定该数列的首项和公差,可求得数列 的通项公式,由 可判断A
选项的正误;利用 的表达式可判断BC选项的正误;求出 ,可判断D选项的正误.
【详解】
当 且 时,由 ,
由 可得 ,
整理得 ( 且 ).
则 为以2为首项,以2为公差的等差数列 , .
A中,当 时, ,A选项正确;
B中, 为等差数列,显然有 ,B选项正确;
C中,记 ,
,,故 为递减数列,
,C选项正确;
D中, , , .
,D选项错误.
故选:D.
【点睛】
关键点点睛:利用 与 的关系求通项,一般利用 来求解,在变形
过程中要注意 是否适用,当利用作差法求解不方便时,应利用 将递推关系
转化为有关 的递推数列来求解.
13.
【分析】
设等差数列{a}的公差为 ,利用等比中项求出 和 的关系,代入 求值即为
n
该等比数列的公比.
【详解】设等差数列{a}的公差为
n
则 ,即 ,解得
则该等比数列的公比为
故答案为:
14.1
【分析】
利用等差、等比的通项公式结合已知求出公差d、公比q,进而求 .
【详解】
若令 公差、 公比分别为 ,
由题意知: ,得 ,
,得 ,
∴ ,
故答案为:1.
15.
【分析】先由题意求得数列 的前几项,进而猜想 ,然后利用数学归纳法证明猜想,
再求得 ,再根据 恒成立对 分奇数、偶数两种情况讨论求得实数 的取值范围
【详解】
解:由题意得 , , ,……
故猜想: ,
下面用数学归纳法证明:
(1)当 时,显然成立;
(2)假设当 时有 ,那么当 时,
所以当 时,也成立,
由(1),(2)得 ,
所以 ,
因为对任意的 , 恒成立,
所以 对任意的 恒成立,
即 对任意的 恒成立,当 为偶数时,有 ,
当 为奇数时,有 ,
所以
所以实数 的取值范围为 ,
故答案为:
【点睛】
关键点点睛:此题考查由递推式求数列的通项公式,考查不等式恒成立问题,解题的关键
是归纳出数列的通项公式,并用数学归纳法证明,以及由 得 ,
然后分类讨论可得结果,考查转化思想,属于中档题
16.1030
【分析】
利用观察法和累加法得到 ,进而求解即可
【详解】
第1行从左至右第6个数字:
第2行从左至右第6个数字: ;第3行从左至右第6个数字: ;
第4行从左至右第6个数字: ;
第5行从左至右第6个数字: ;
……………………………………;
第n行从左至右第6个数字: ;
利用累加法得:
,
,
得,
故答案为:1030
【点睛】
关键点睛:解题的关键在于观察得到,
最后,使用累加法求出数列的通项 ,属于中档题17.(Ⅰ) ;(Ⅱ)证明见解析.
【分析】
(Ⅰ)根据题中条件,令 代入递推式,即可得出结果;
(Ⅱ)根据递推公式,得到 ,得出
,计算 ,即可得出结论成立.
【详解】
(Ⅰ)因为 , , , ,
当 时, ,
即 ,解得 .
(Ⅱ)证明:由 ,得
,
即 .
当 时,有 ,∴ ,∴ ,
∴数列 是以 为首项, 为公比的等比数列.
【点睛】
本题主要考查由递推公式求数列中的项,考查证明数列是等比数列,属于常考题型.
18.(1) ;(2) .
【分析】
(1)先由题中条件,求 ;再由 ,根据题中条件,得到 ,
判定数列为等比数列,进而可求出其通项公式;
(2)由(1),根据题中条件,得到 ,求出 ,再由裂项相消的
方法,即可求出数列的和.
【详解】
(1)当 时, .
当 时, ,又 , ,
即数列 是首项为 ,公比为 的等比数列,故 .(2)由已知得 ,
,
.
.
.
【点睛】
本题主要考查由递推公式求等比数列的通项公式,考查裂项相消法求数列的和,属于常考
题型.
19.(Ⅰ)证明见解析;(Ⅱ)证明见解析.
【分析】
(1)根据 为等差数列,利用倒序相加法证明 即可;
(2)由前n项和公式有 、 ,相加后整理可得
, 为等差数列得证.
【详解】
(Ⅰ)证明:已知数列 为等差数列,设其公差为d,则有 ,
于是 ,①
又 ,②
①+②得: ,即 .
(Ⅱ)证明:∵ ,当 时, ,
∴ ,③
,④
④-③并整理,得 ,即 ,
∴数列 是等差数列.
【点睛】
本题考查了已知等差数列的通项公式,应用倒序相加法求证前n项和公式,由前n项和公
式,结合等差数列的定义证明等差数列,属于基础题.
20.(1)证明见解析, ;(2)证明见解析.
【分析】(1)由已知条件可得 ,从而可证得 是等比数列,再由等比数
列的通项公式可得 ,而可求得 ,
(2)利用错位相减法求出 ,再利用放缩法可证得结论
【详解】
(1)因为 , ,
所以 .
又 ,所以 是首项为 ,公比为 的等比数列.
于是 ,故 .
(2) .
两边同乘以 得 .
以上两式相减得 .故 .
【点睛】
此题考查由递推式证明等比数列,考查错位相减法的应用,考查计算能力,属于基础题
21.(1) ; ;(2)数列 不是等比数列.理由见解析.
【分析】
(1)由等差数列的通项公式以及前 项和公式即可求得 ,代入 ,利用裂项求和
即可求得数列 的前n项和;
(2)由 求出数列 的通项公式,再运用等比数列的定义判断即可.
【详解】
解:(1)设数列 的公差为d,
,
,
又 ,
解得: , ,,
,
设 前n项的和为 ,
;
(2) , ,
.
当 时, ;
当 时, ,
,
若 是等比数列,则有 ,
而 , ,所以与 矛盾,故数列 不是等比数列.
【点睛】
方法点睛:数列求和的方法技巧:
(1)倒序相加:用于等差数列、与二项式系数、对称性相关联的数列的求和.
(2)错位相减:用于等差数列与等比数列的积数列的求和.
(3)分组求和:用于若干个等差或等比数列的和或差数列的求和.
22.(1)证明见解析; ; , ;(2)
.
【分析】
(1)根据等比数列的定义计算 即可证出,然后求出数列 的通项公式,进而
可求出数列 通项公式;将 , 用基本量 表示,解方程组即可求出
,进而可求出数列 的通项公式;
(2)根据(1)可得 ,利用错位相减法即可求出数列 的前
项和 .
【详解】(1) ,
所以数列 是首项为 ,公比 等比数列,
所以 ,即 , ;
由 ,解得 , ,所以
(2)由(1)知 ,
所以 ,①
,
②
①-②得 ,,
所以 .
【点睛】
方法点睛:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,
那么求这个数列的前 项和即可用错位相减法求解.①在写出 与 的表达式时,应特
别注意将两式“错位对齐”,以便下一步准确写出 ;②作差后,应注意减式中所
剩各项的符号要变号.