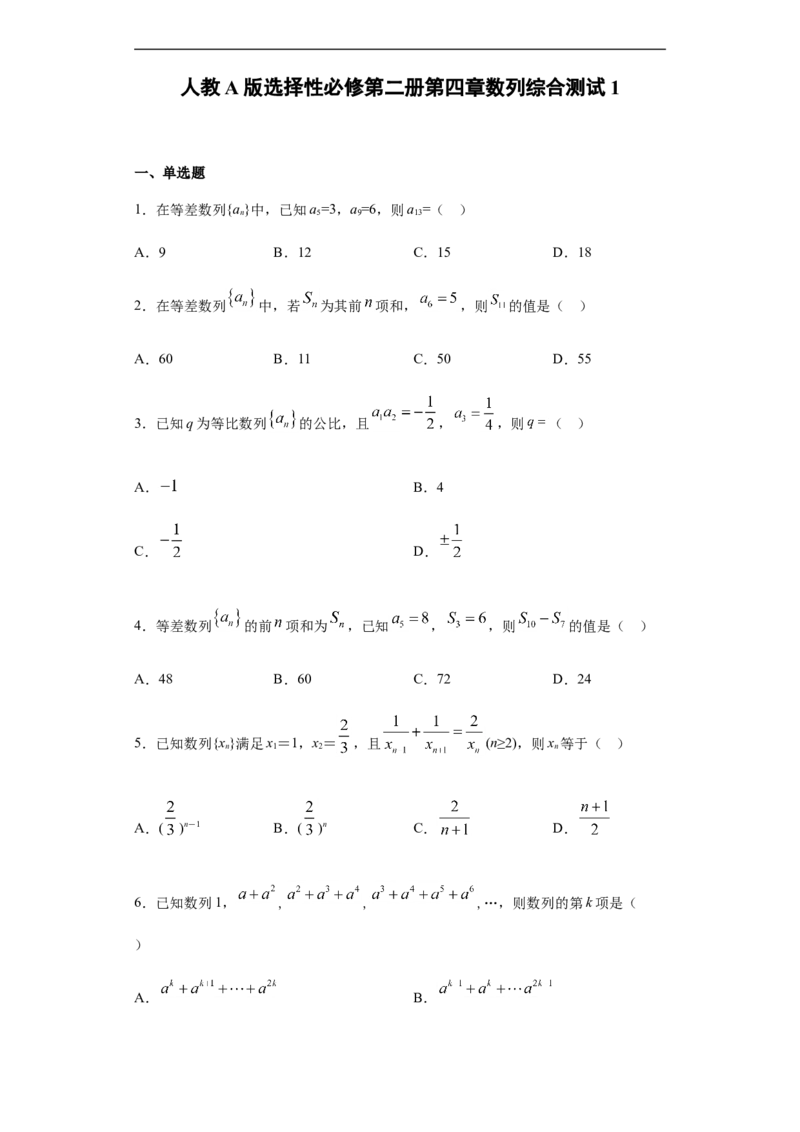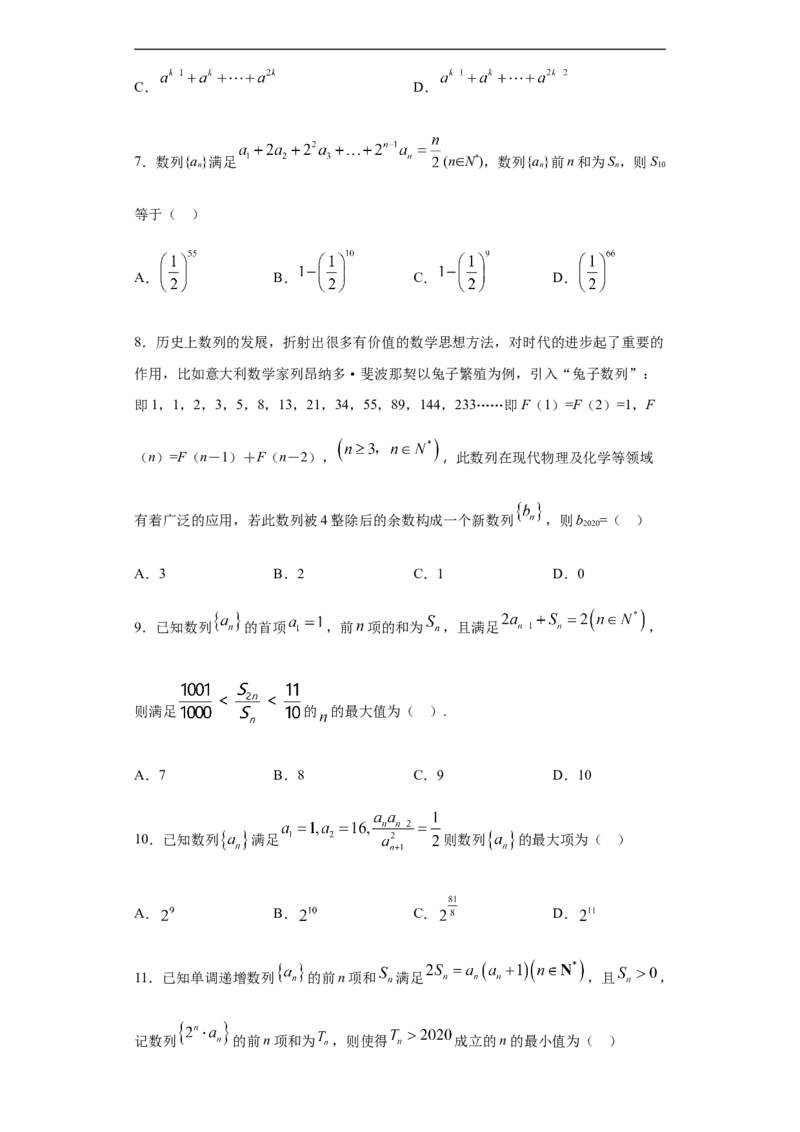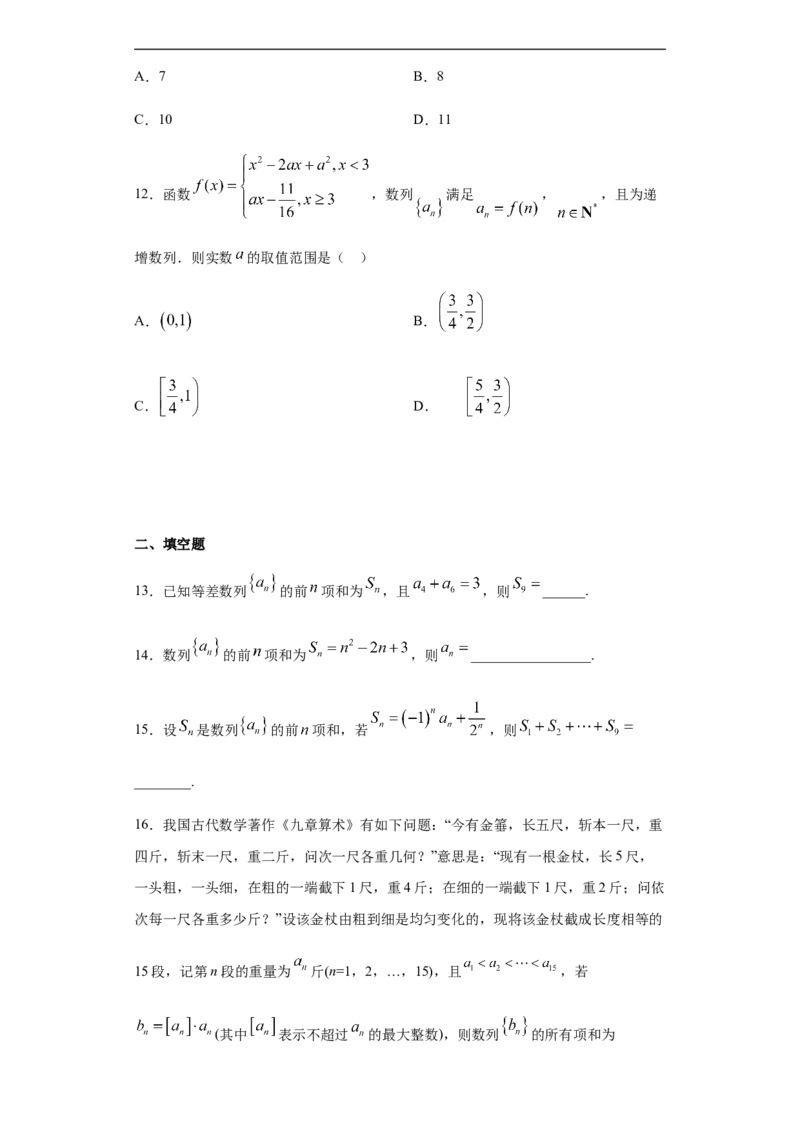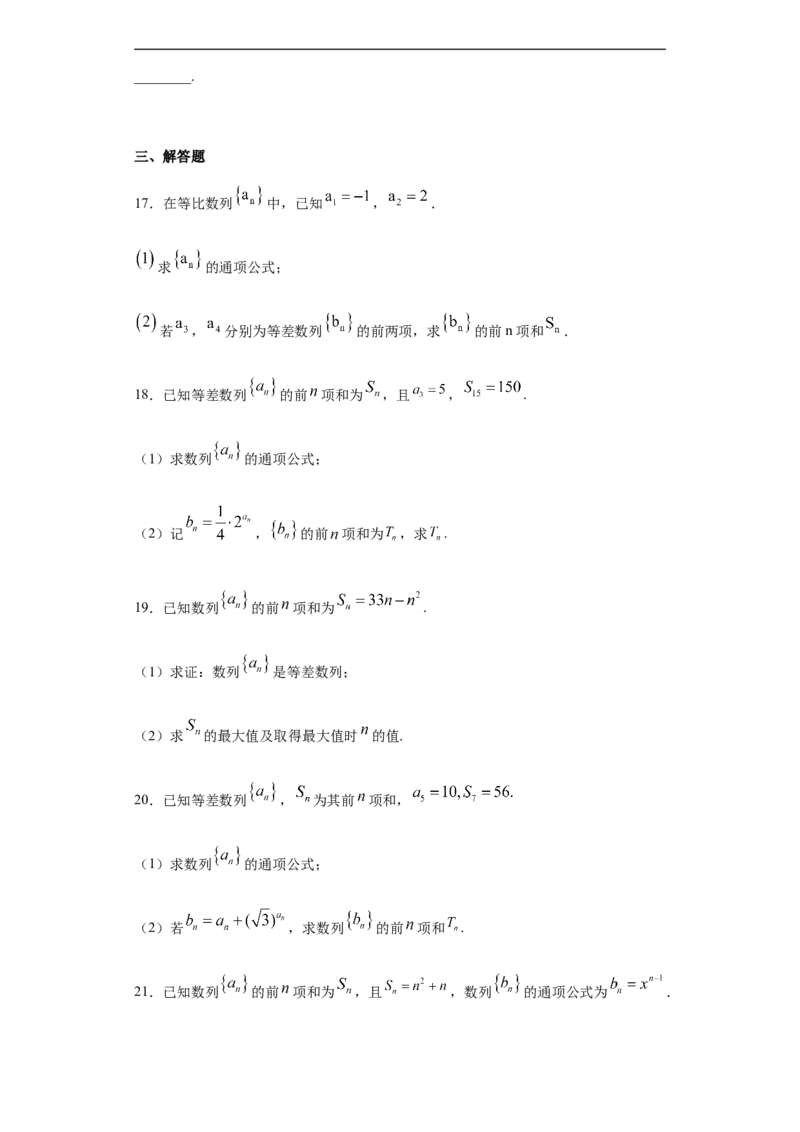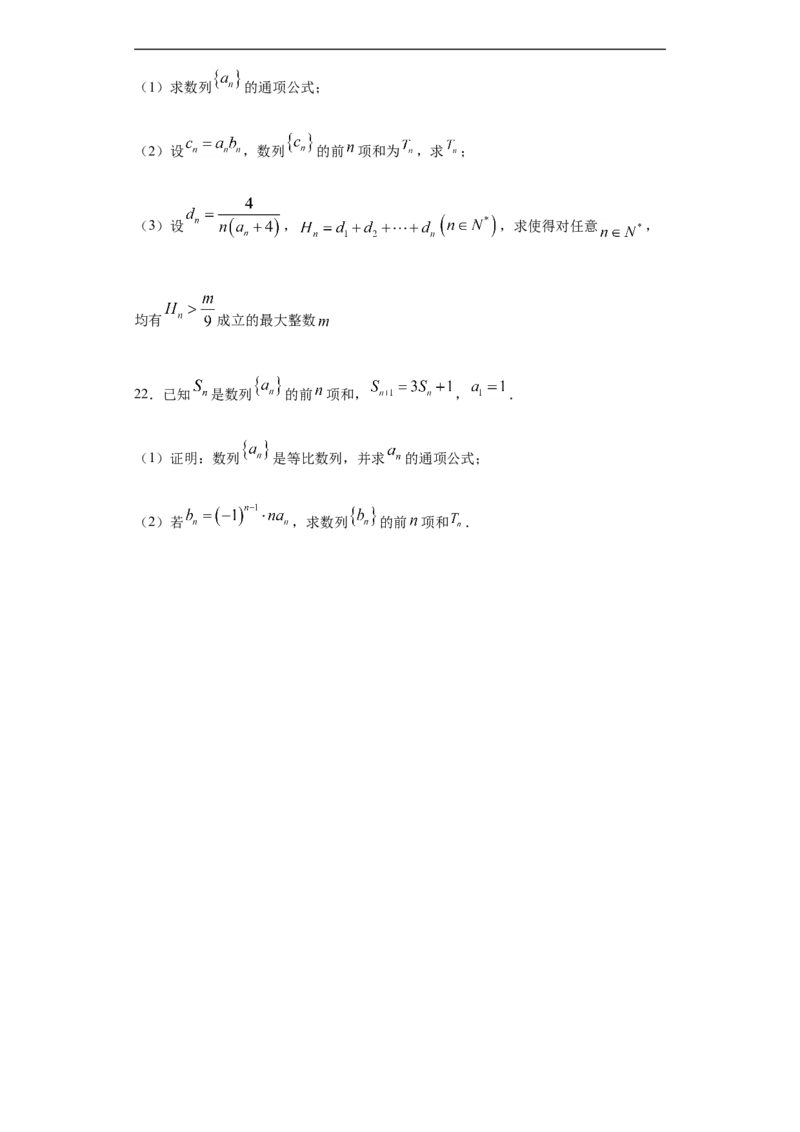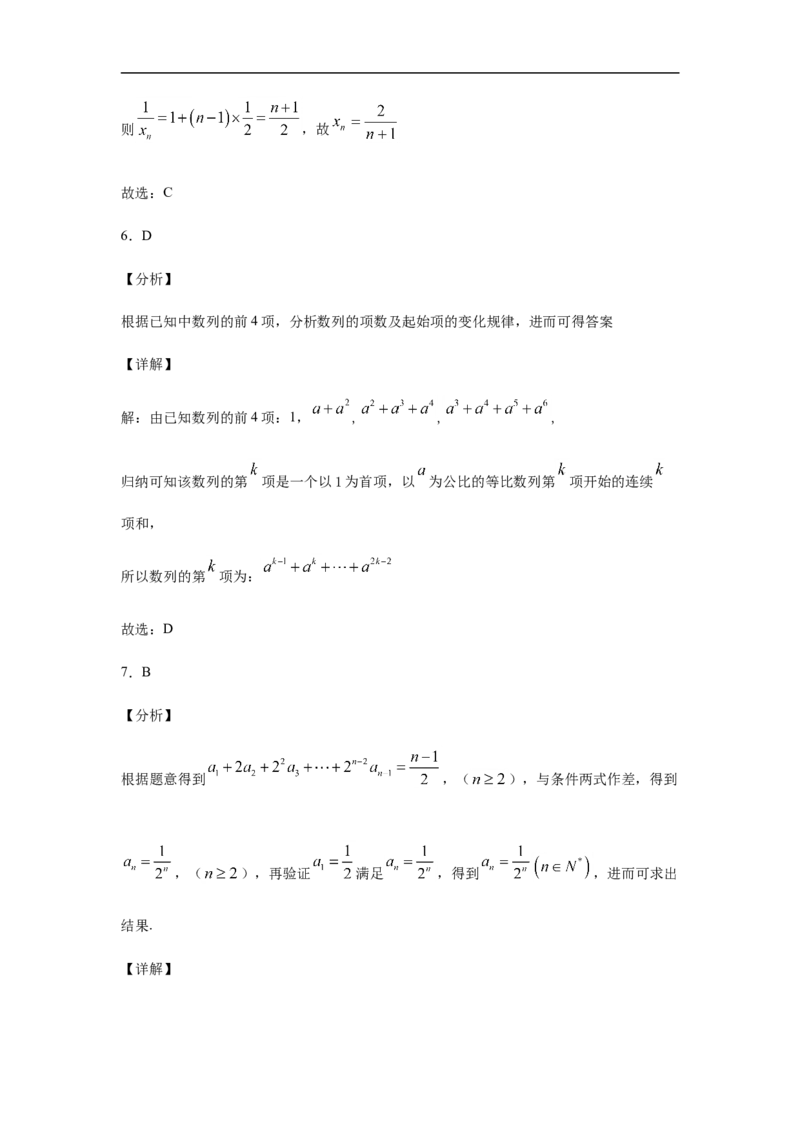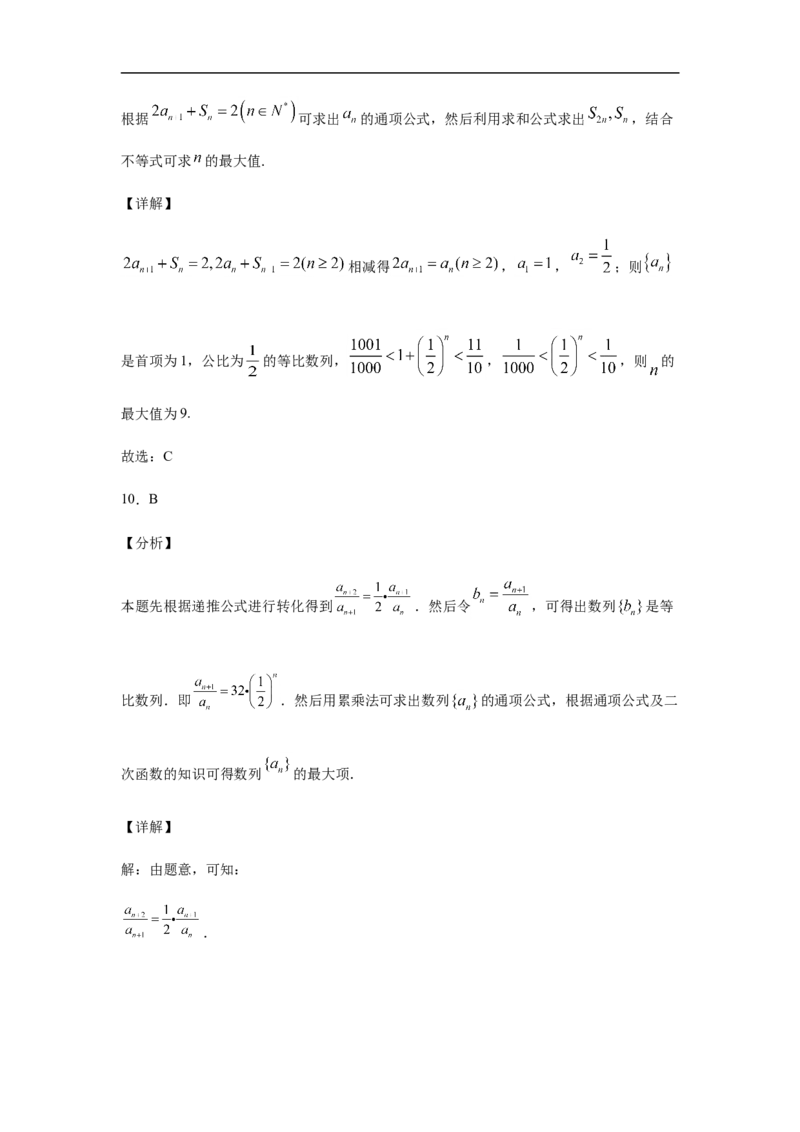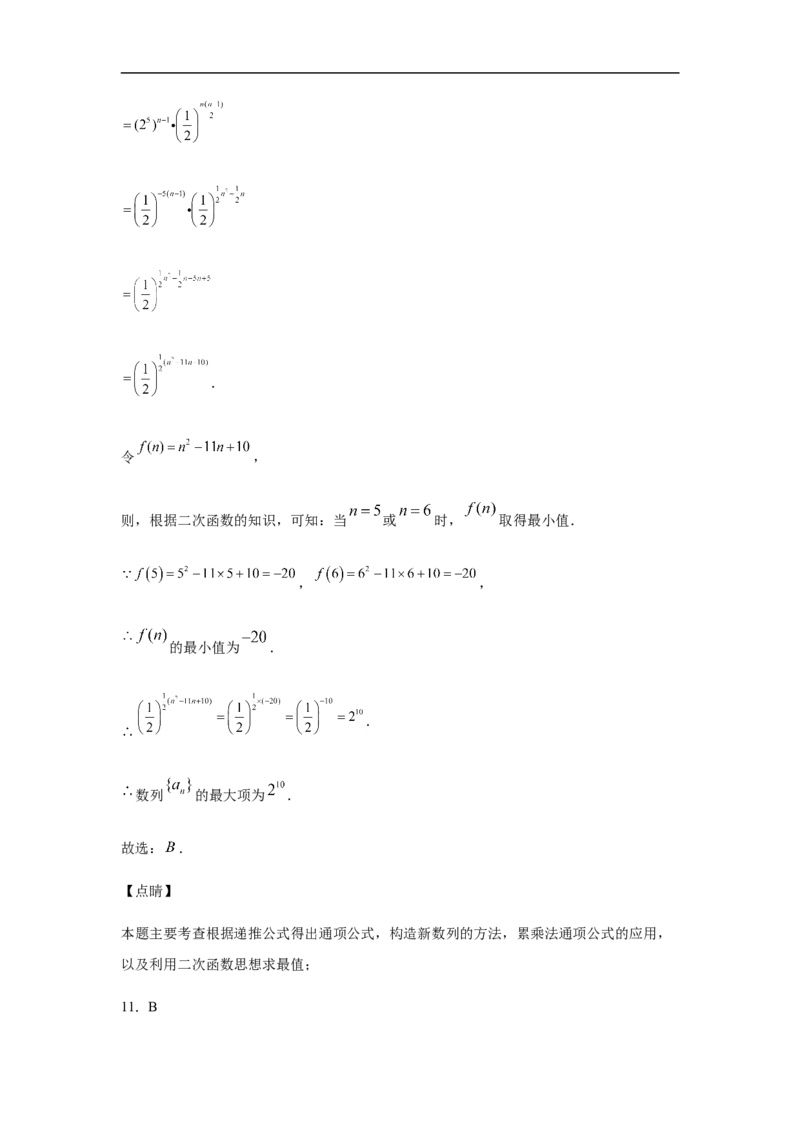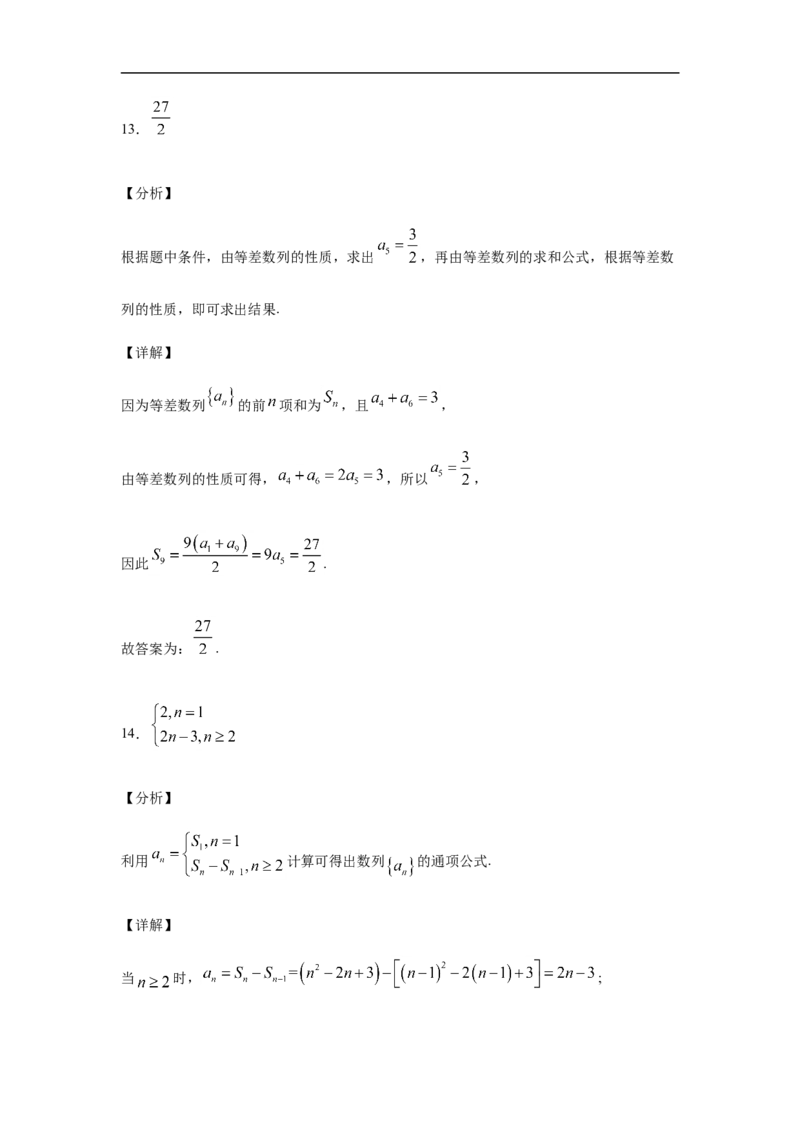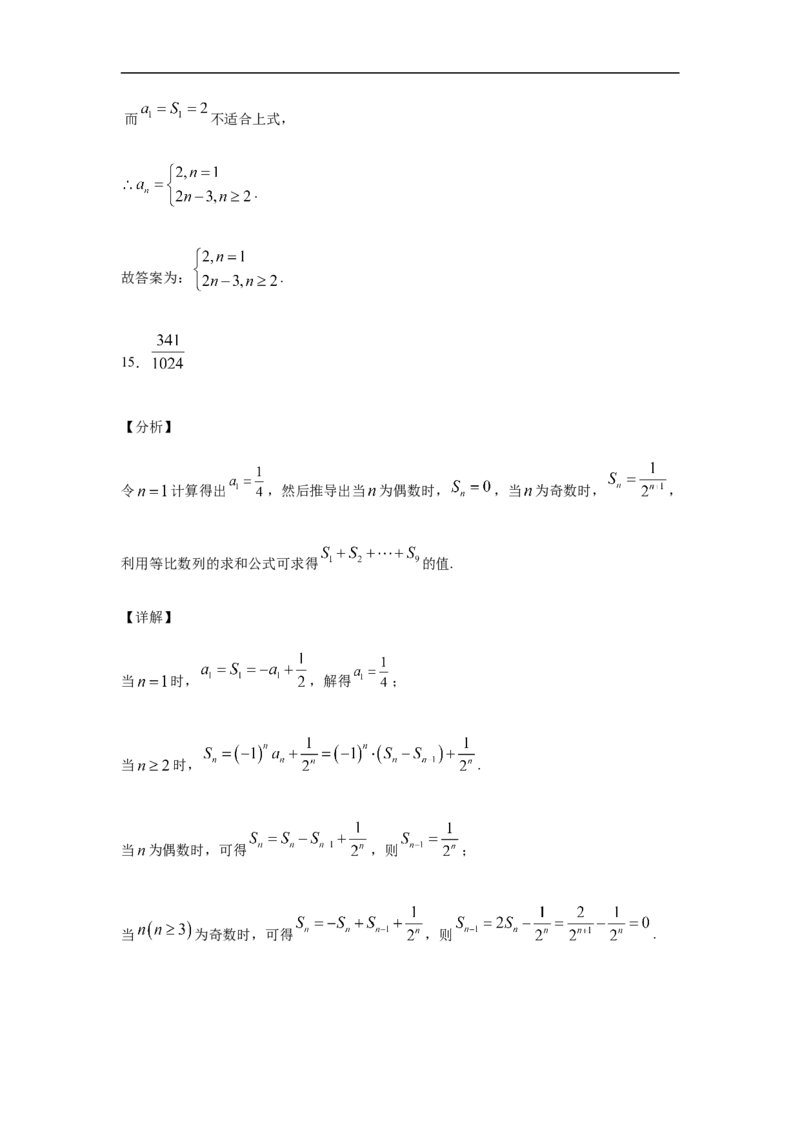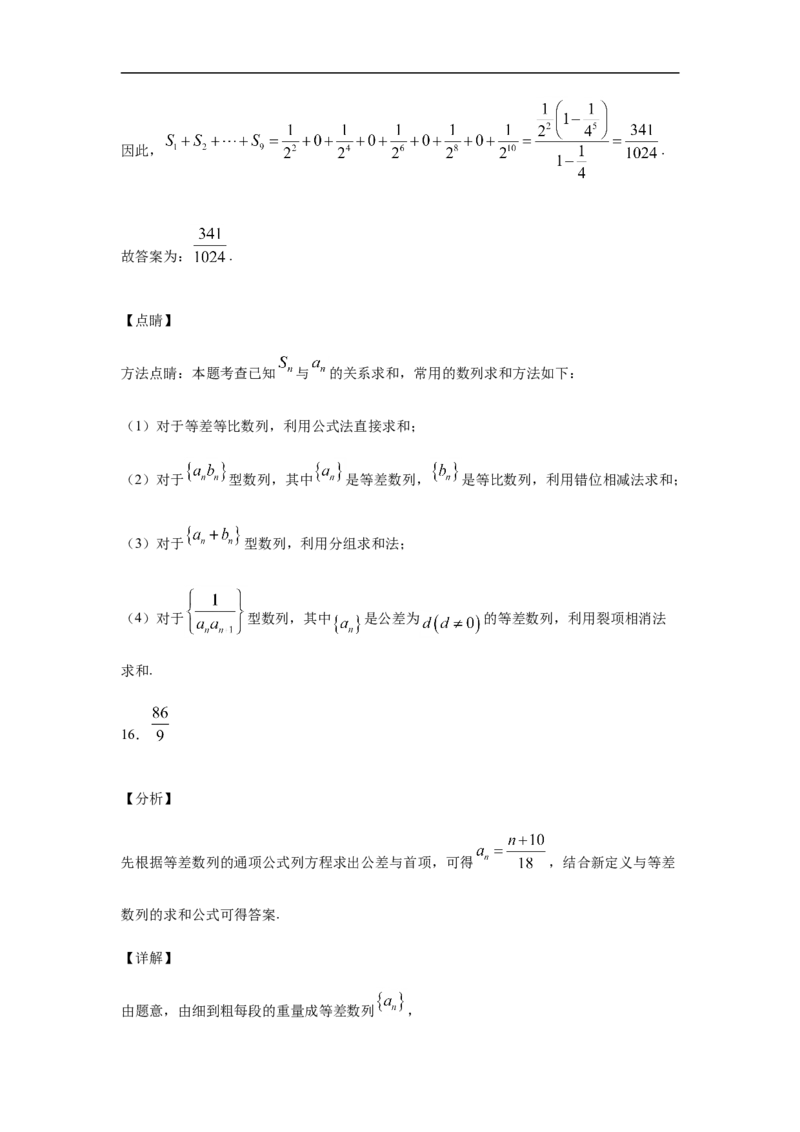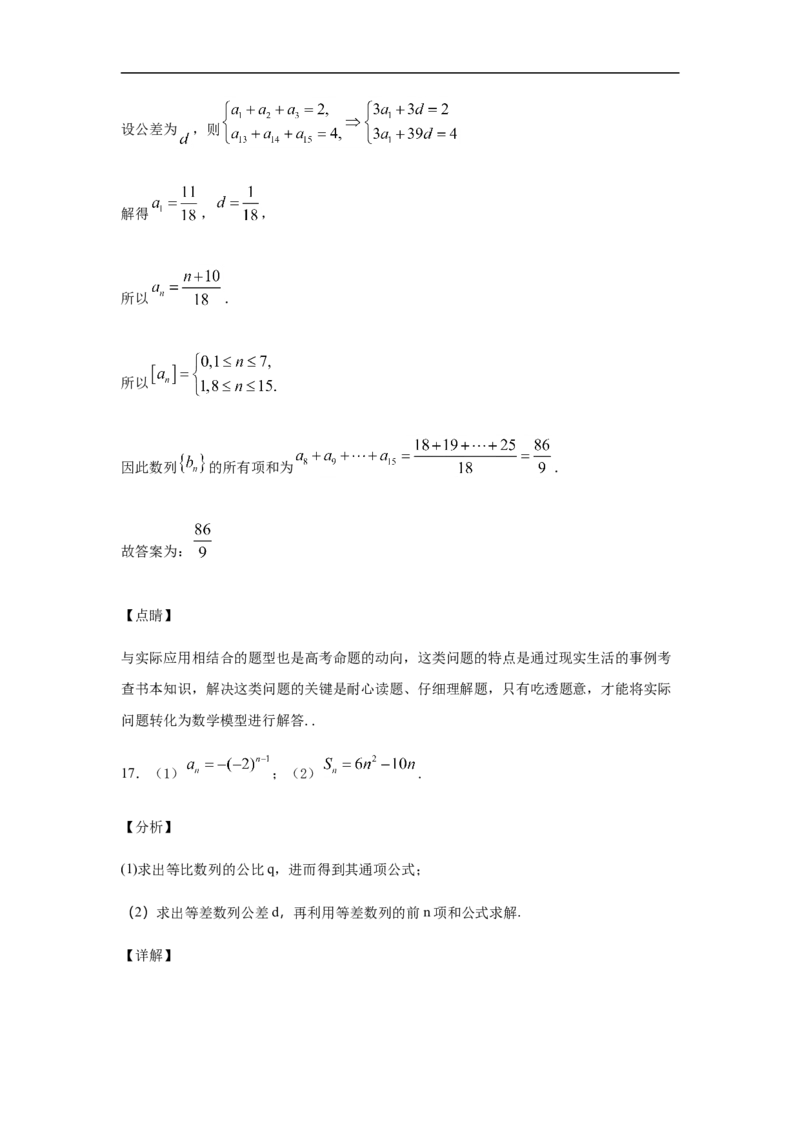文档内容
人教A版选择性必修第二册第四章数列综合测试1
一、单选题
1.在等差数列{a}中,已知a=3,a=6,则a =( )
n 5 9 13
A.9 B.12 C.15 D.18
2.在等差数列 中,若 为其前 项和, ,则 的值是( )
A.60 B.11 C.50 D.55
3.已知q为等比数列 的公比,且 , ,则 ( )
A. B.4
C. D.
4.等差数列 的前 项和为 ,已知 , ,则 的值是( )
A.48 B.60 C.72 D.24
5.已知数列{x}满足x=1,x= ,且 (n≥2),则x 等于( )
n 1 2 n
A.( )n-1 B.( )n C. D.
6.已知数列1, , , ,…,则数列的第k项是(
)
A. B.C. D.
7.数列{a}满足 (n∈N*),数列{a}前n和为S,则S
n n n 10
等于( )
A. B. C. D.
8.历史上数列的发展,折射出很多有价值的数学思想方法,对时代的进步起了重要的
作用,比如意大利数学家列昂纳多·斐波那契以兔子繁殖为例,引入“兔子数列”:
即1,1,2,3,5,8,13,21,34,55,89,144,233……即F(1)=F(2)=1,F
(n)=F(n-1)+F(n-2), ,此数列在现代物理及化学等领域
有着广泛的应用,若此数列被4整除后的余数构成一个新数列 ,则b =( )
2020
A.3 B.2 C.1 D.0
9.已知数列 的首项 ,前 项的和为 ,且满足 ,
则满足 的 的最大值为( ).
A.7 B.8 C.9 D.10
10.已知数列 满足 则数列 的最大项为( )
A. B. C. D.
11.已知单调递增数列 的前n项和 满足 ,且 ,
记数列 的前n项和为 ,则使得 成立的n的最小值为( )A.7 B.8
C.10 D.11
12.函数 ,数列 满足 , ,且为递
增数列.则实数 的取值范围是( )
A. B.
C. D.
二、填空题
13.已知等差数列 的前 项和为 ,且 ,则 ______.
14.数列 的前 项和为 ,则 _________________.
15.设 是数列 的前 项和,若 ,则
________.
16.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重
四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金杖,长5尺,
一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依
次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,现将该金杖截成长度相等的
15段,记第n段的重量为 斤(n=1,2,…,15),且 ,若
(其中 表示不超过 的最大整数),则数列 的所有项和为________.
三、解答题
17.在等比数列 中,已知 , .
求 的通项公式;
若 , 分别为等差数列 的前两项,求 的前 项和 .
n
18.已知等差数列 的前 项和为 ,且 , .
(1)求数列 的通项公式;
(2)记 , 的前 项和为 ,求 .
19.已知数列 的前 项和为 .
(1)求证:数列 是等差数列;
(2)求 的最大值及取得最大值时 的值.
20.已知等差数列 , 为其前 项和,
(1)求数列 的通项公式;
(2)若 ,求数列 的前 项和 .
21.已知数列 的前 项和为 ,且 ,数列 的通项公式为 .(1)求数列 的通项公式;
(2)设 ,数列 的前 项和为 ,求 ;
(3)设 , ,求使得对任意 ,
均有 成立的最大整数
22.已知 是数列 的前 项和, , .
(1)证明:数列 是等比数列,并求 的通项公式;
(2)若 ,求数列 的前 项和 .参考答案
1.A
【分析】
在等差数列{a}中,利用等差中项由 求解.
n
【详解】
在等差数列{a}中,a=3,a=6,
n 5 9
所以 ,
所以 ,
故选:A
2.D
【分析】
根据题中条件,由等差数列的性质,以及等差数列的求和公式,即可求出结果.
【详解】
因为在等差数列 中,若 为其前 项和, ,
所以 .
故选:D.
3.C
【分析】
利用等比通项公式直接代入计算,即可得答案;【详解】
,
故选:C.
4.A
【分析】
根据条件列方程组,求首项和公差,再根据 ,代入求值.
【详解】
由条件可知 ,解得: ,
.
故选:A
5.C
【分析】
由已知可得数列 是等差数列,求出数列 的通项公式,进而得出答案.
【详解】
由已知可得数列 是等差数列,且 ,故公差则 ,故
故选:C
6.D
【分析】
根据已知中数列的前4项,分析数列的项数及起始项的变化规律,进而可得答案
【详解】
解:由已知数列的前4项:1, , , ,
归纳可知该数列的第 项是一个以1为首项,以 为公比的等比数列第 项开始的连续
项和,
所以数列的第 项为:
故选:D
7.B
【分析】
根据题意得到 ,( ),与条件两式作差,得到
,( ),再验证 满足 ,得到 ,进而可求出
结果.
【详解】因为数列 满足 ,
,( )
则 ,则 ,( ),
又 满足 ,所以 ,
因此 .
故选:B
8.A
【分析】
根据条件得出数列 的周期即可.
【详解】
由题意可知“兔子数列”被4整除后的余数构成一个新数列为:1,1,2,3,1,0,1,
1,2,3,1,0,……
则可得到周期为6,所以b =b=3,
2020 4
故选:A
9.C
【分析】根据 可求出 的通项公式,然后利用求和公式求出 ,结合
不等式可求 的最大值.
【详解】
相减得 , , ;则
是首项为1,公比为 的等比数列, , ,则 的
最大值为9.
故选:C
10.B
【分析】
本题先根据递推公式进行转化得到 .然后令 ,可得出数列 是等
比数列.即 .然后用累乘法可求出数列 的通项公式,根据通项公式及二
次函数的知识可得数列 的最大项.
【详解】
解:由题意,可知:
.令 ,则 .
,
数列 是以 为首项, 为公比的等比数列.
.
.
,
,
.
各项相乘,可得:
..
令 ,
则,根据二次函数的知识,可知:当 或 时, 取得最小值.
, ,
的最小值为 .
.
数列 的最大项为 .
故选: .
【点睛】
本题主要考查根据递推公式得出通项公式,构造新数列的方法,累乘法通项公式的应用,
以及利用二次函数思想求最值;
11.B【分析】
由数列 与 的关系转化条件可得 ,结合等差数列的性质可得 ,再由
错位相减法可得 ,即可得解.
【详解】
由题意, ,
当 时, ,
所以 ,
整理得 ,
因为数列 单调递增且 ,所以 ,即 ,
当 时, ,所以 ,
所以数列 是以 为首项,公差为1的等差数列,
所以 ,
所以 ,
,
所以 ,所以 ,
所以 , ,
所以 成立的n的最小值为8.
故选:B.
【点睛】
关键点点睛:解决本题的关键是数列 与 关系的应用及错位相减法的应用.
12.B
【分析】
根据分段函数的特征,以及数列在 是单调递增数列,列式求解.
【详解】
是单调递增数列,所以 ,数列
是单调递增数列 .
故选:B.
【点睛】
易错点点睛:本题考查分段函数的单调性和数列单调性的简单综合应用,本地的易错点是
和 时,数列的单调性,容易和函数 时函数单调性搞混,
此时函数单调性和数列单调性的式子是不一样的,需注意这点.13.
【分析】
根据题中条件,由等差数列的性质,求出 ,再由等差数列的求和公式,根据等差数
列的性质,即可求出结果.
【详解】
因为等差数列 的前 项和为 ,且 ,
由等差数列的性质可得, ,所以 ,
因此 .
故答案为: .
14.
【分析】
利用 计算可得出数列 的通项公式.
【详解】
当 时, ;而 不适合上式,
.
故答案为: .
15.
【分析】
令 计算得出 ,然后推导出当 为偶数时, ,当 为奇数时, ,
利用等比数列的求和公式可求得 的值.
【详解】
当 时, ,解得 ;
当 时, .
当 为偶数时,可得 ,则 ;
当 为奇数时,可得 ,则 .因此, .
故答案为: .
【点睛】
方法点睛:本题考查已知 与 的关系求和,常用的数列求和方法如下:
(1)对于等差等比数列,利用公式法直接求和;
(2)对于 型数列,其中 是等差数列, 是等比数列,利用错位相减法求和;
(3)对于 型数列,利用分组求和法;
(4)对于 型数列,其中 是公差为 的等差数列,利用裂项相消法
求和.
16.
【分析】
先根据等差数列的通项公式列方程求出公差与首项,可得 ,结合新定义与等差
数列的求和公式可得答案.
【详解】
由题意,由细到粗每段的重量成等差数列 ,设公差为 ,则
解得 , ,
所以 .
所以
因此数列 的所有项和为 .
故答案为:
【点睛】
与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考
查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际
问题转化为数学模型进行解答..
17.(1) ;(2) .
【分析】
(1)求出等比数列的公比q,进而得到其通项公式;
(2)求出等差数列公差d,再利用等差数列的前n项和公式求解.
【详解】(1)∵公比 ,∴ .
(2)∵ , , - 8+4=12,
∴ ,公差 .
故 .
【点睛】
本题考查了等比数列的基本量计算和等比数列的通项公式,考查了等差数列的基本量计算
和前n项和公式.是基础题.
18.(1) (2)
【分析】
(1)由 ,可得 ,即 ,从而可得公差 ,从而得出答案.
(2)由条件可得 ,由等比数列的前 项和公式可得答案.
【详解】
(1)设等差数列 的公差为 ,
则 ,又 , ,又
,得 ,则所以
(2)
所以
19.(1)证明见解析;(2)前16项或前17项和最大,最大值为 .
【分析】
(1)先由 求 通项公式,再利用定义法证明即可;
(2)先判断 的n的范围,得到数列的正负分布,即得何时 最大.
【详解】
解:(1)证明:当 时, ,
又当 时, ,满足 ,
故 的通项公式为 ,
∴ .
故数列 是以32为首项, 为公差的等差数列;
(2)令 ,即 ,解得 ,
故数列 的前16项或前17项和最大,此时 .
20.(1) ;(2) .
【分析】
(1)设数列 的首项为 ,公差为 ,然后根据题目条件列出关于 和 的方程组求
解;
(2)将(1)中所得的数列 的通项公式代入,得到 的通项公式,再根据通项公式确
定该用哪个方法求前 项和.
【详解】
解:(1)设数列 的首项为 ,公差为 ,则根据题意得:
由 ,解得 ,所以 .
(2) ,则
.【点睛】
本题考查等差数列的基本公式的运用,考查利用分组求和法求数列的前 项和. 解答时,如
果已知数列为等差数列或等比数列求通项公式,只需将题目条件翻译成数学表达式,然后
通过方程解出首项和公差或公比,然后得出数列的通项公式. 对于数列 ,当
和 分别为等差数列与等比数列时,可采用分组求和法求和.
21.(1) ;(2) ;(3)存在最大的整数
满足题意.
【分析】
(1)当 时, ;当 时, ,将已知代入化简计算可得数列
的通项公式;
(2)利用错位相减法计算 ,分 和 两种情况,分别得出答案;
(3)利用裂项相消法计算出 ,并得出单调性和最值,代入不等式解出 的范围,得到
答案.
【详解】
(1)当 时,
当 时,
即数列 的通项公式为(2) , ,①
则 ,②
①﹣②,得 .
当 时, ,则 .
当 时,
综上可得,
(3)由(1)可得 ,
则
显然 为关于 的增函数,故 .
于是欲使 恒成立,
则 ,解得 .存在最大的整数 满足题意.
【点睛】
方法点睛:本题考查数列的通项公式,考查数列的求和,数列求和的方法总结如下:
1.公式法,利用等差数列和等比数列的求和公式进行计算即可;
2.裂项相消法,通过把数列的通项公式拆成两项之差,在求和时中间的一些项可以相互抵
消,从而求出数列的和;
3.错位相减法,当数列的通项公式由一个等差数列与一个等比数列的乘积构成时使用此方
法;
4.倒序相加法,如果一个数列满足首末两项等距离的两项之和相等,可以使用此方法求和.
22.(1)证明见解析, ;(2) .
【分析】
(1)首先根据 , 两式相减得 ,即可得到
的通项公式.
(2)首先求出 ,再利用错位相减法求前 项和 即可.
【详解】
(1)证明:由 ,当 时, ,
两式相减得 ,
当 时, 即 ,∴ ,∴ ,
∴ 时都有 ,∴数列 是首项为1,公比为3的等比数列,∴ .
(2)解: ,
∴ ,
,
∴ ,
∴
∴ .
【点睛】
方法点睛:
本题主要考查数列的求和,常见的数列求和方法如下:
1.公式法:直接利用等差、等比数列的求和公式计算即可;
2.分组求和法:把需要求和的数列分成熟悉的数列,再求和即可;
3.裂项求和法:通过把数列的通项公式拆成两项之差,再求和即可;
4.错位相减法:当数列的通项公式由一个等差数列和一个等比数列的乘积构成时,可使用
此方法求和.