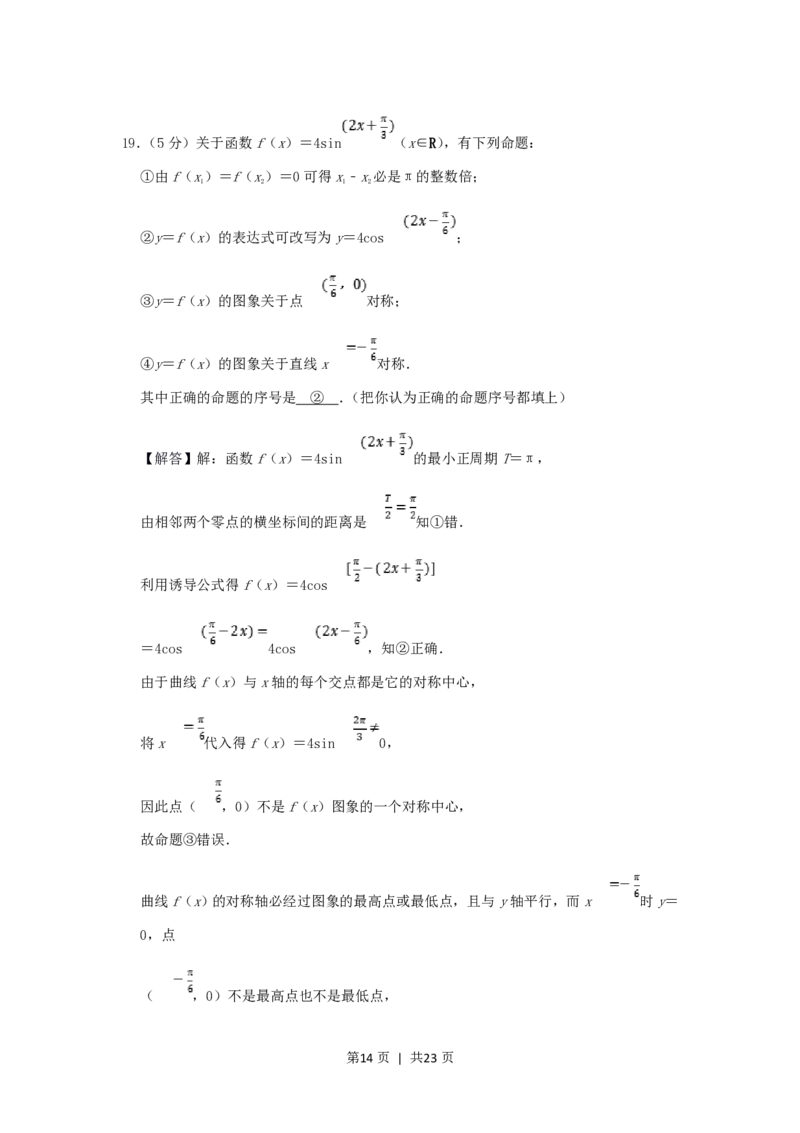文档内容
1998 年湖北高考理科数学真题及答案
一、选择题(共15小题,每小题4分,满分60分)
1.(4分)sin330°等于( )
A. B. C. D.
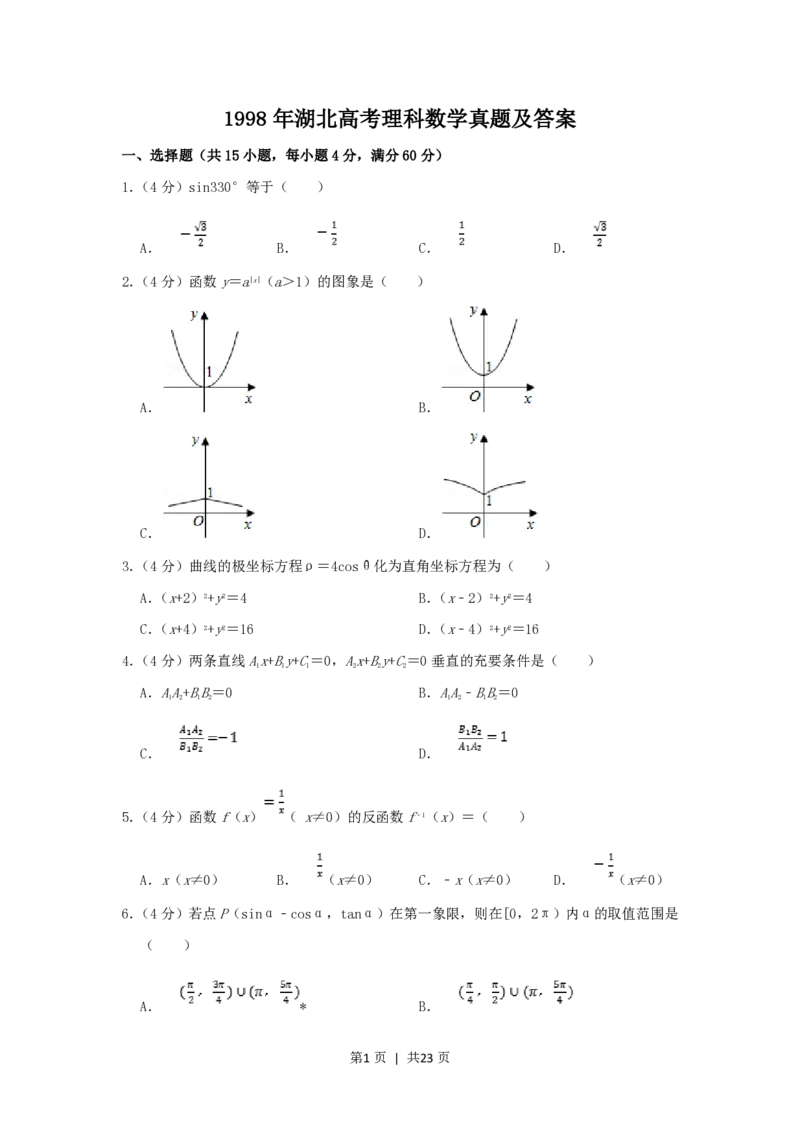
2.(4分)函数y=a|x|(a>1)的图象是( )
A. B.
C. D.
3.(4分)曲线的极坐标方程ρ=4cosθ化为直角坐标方程为( )
A.(x+2)2+y2=4 B.(x﹣2)2+y2=4
C.(x+4)2+y2=16 D.(x﹣4)2+y2=16
4.(4分)两条直线Ax+By+C=0,Ax+By+C=0垂直的充要条件是( )
1 1 1 2 2 2
A.AA+BB=0 B.AA﹣BB=0
1 2 1 2 1 2 1 2
C. D.
5.(4分)函数f(x) ( x≠0)的反函数f﹣1(x)=( )
A.x(x≠0) B. (x≠0) C.﹣x(x≠0) D. (x≠0)
6.(4分)若点P(sinα﹣cosα,tanα)在第一象限,则在[0,2π)内α的取值范围是
( )
A. * B.
第1页 | 共23页C. D.
7.(4分)已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为
( )
A.120° B.150° C.180° D.240°
8.(4分)复数﹣i的一个立方根是i,它的另外两个立方根是( )
A. i B. i C.± i D.± i
9.(4分)如果棱台的两底面积分别是S,S′,中截面的面积是S,那么( )
0
A.2 B.S C.2S=S+S′
0 0
D.S2=2S'S
0
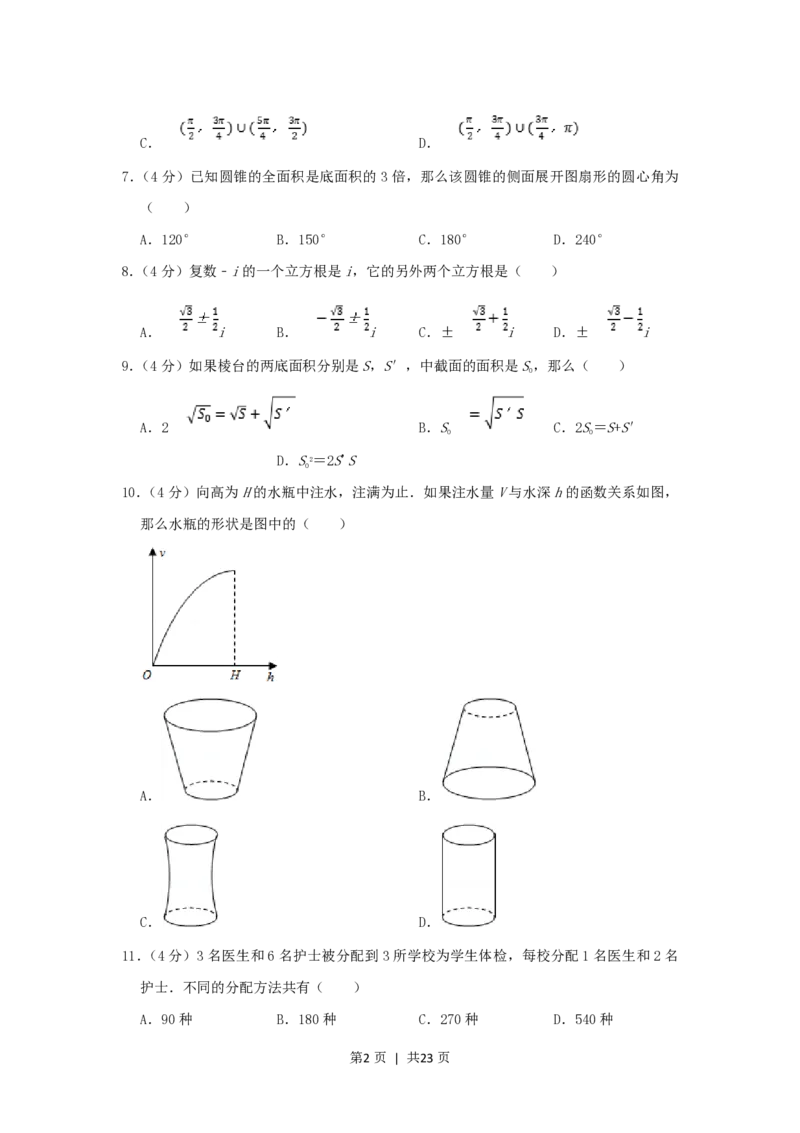
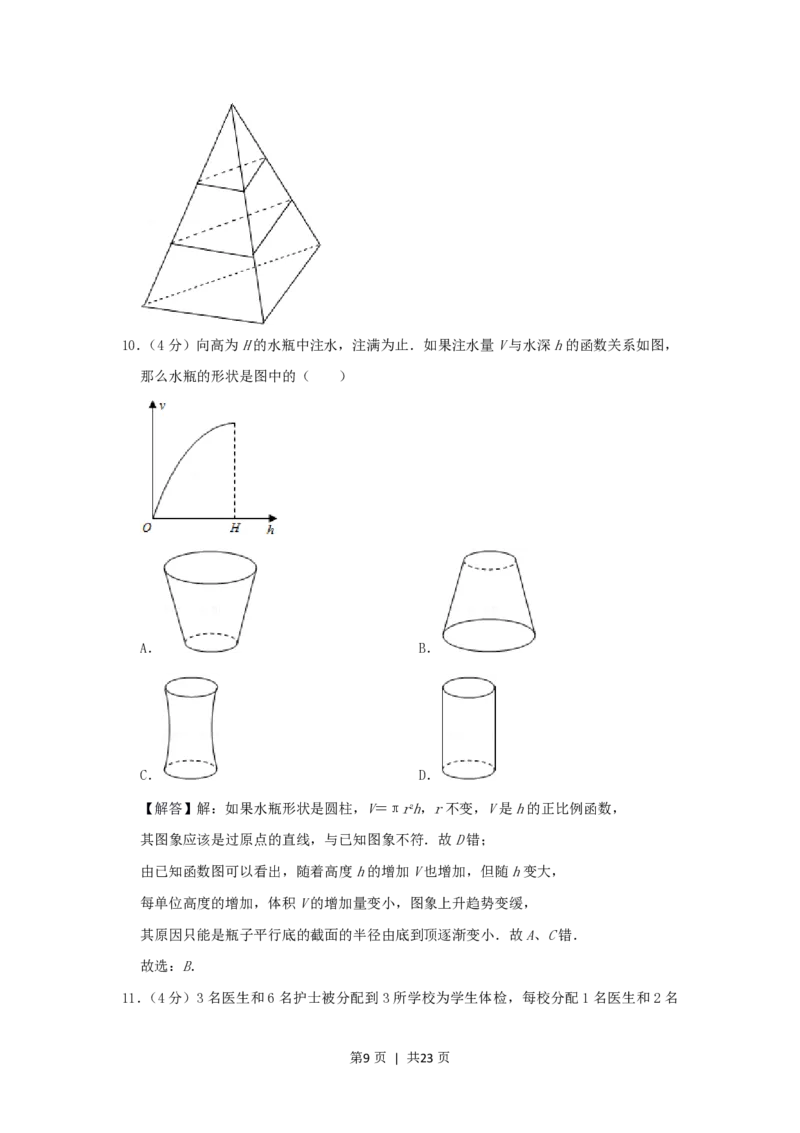
10.(4分)向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系如图,
那么水瓶的形状是图中的( )
A. B.
C. D.
11.(4分)3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名
护士.不同的分配方法共有( )
A.90种 B.180种 C.270种 D.540种
第2页 | 共23页12.(4分)椭圆 1的焦点为F和F,点P在椭圆上,如果线段PF的中点在y轴上,
1 2 1
那么|PF|是|PF|的( )
1 2
A.7倍 B.5倍 C.4倍 D.3倍
13.(4分)球面上有3个点,其中任意两点的球面距离都等于大圆周长的 ,经过这3个点
的小圆的周长为4π,那么这个球的半径为( )
A.4 B.2 C.2 D.
14.(4分)一个直角三角形三内角的正弦值成等比数列,其最小内角是( )
A.arccos B.arcsin C.arccos D.arcsin
15.(4分)在等比数列{a}中,a>1,且前n项和S满足 S ,那么a的取值范围
n 1 n n 1
是( )
A.(1,+∞) B.(1,4) C.(1,2) D.(1, )
二、填空题(共4小题,每小题5分,满分20分)
16.(5分)已知圆C过双曲线 1的一个顶点和一个焦点,且圆心在此双曲线上,则
圆心到双曲线中心的距离是 .
17.(5分)(x+2)10(x2﹣1)的展开式中x10的系数为 (用数字作答).
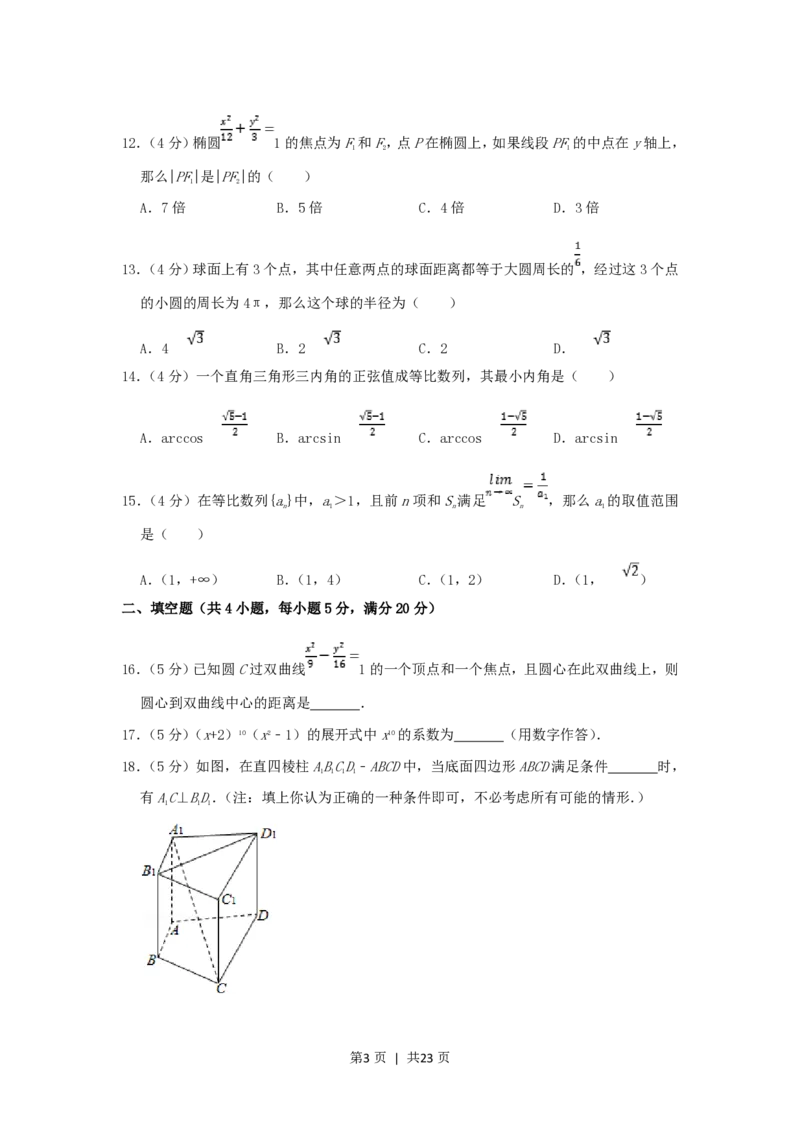
18.(5分)如图,在直四棱柱ABCD﹣ABCD中,当底面四边形ABCD满足条件 时,
1 1 1 1
有AC⊥BD.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
1 1 1
第3页 | 共23页19.(5分)关于函数f(x)=4sin (x∈R),有下列命题:
①由f(x)=f(x)=0可得x﹣x必是π的整数倍;
1 2 1 2
②y=f(x)的表达式可改写为y=4cos ;
③y=f(x)的图象关于点 对称;
④y=f(x)的图象关于直线x 对称.
其中正确的命题的序号是 .(把你认为正确的命题序号都填上)
三、解答题(共6小题,满分70分)
20.(10分)在△ABC中,a,b,c分别是角A,B,C的对边,设a+c=2b,A﹣C .求sinB
的值.以下公式供解题时参考:
sinθ+sin∅=2sin cos ,
sinθ﹣sin∅=2cos sin ,
cosθ+cos∅=2cos cos ,
cosθ﹣cos∅=﹣2sin sin .
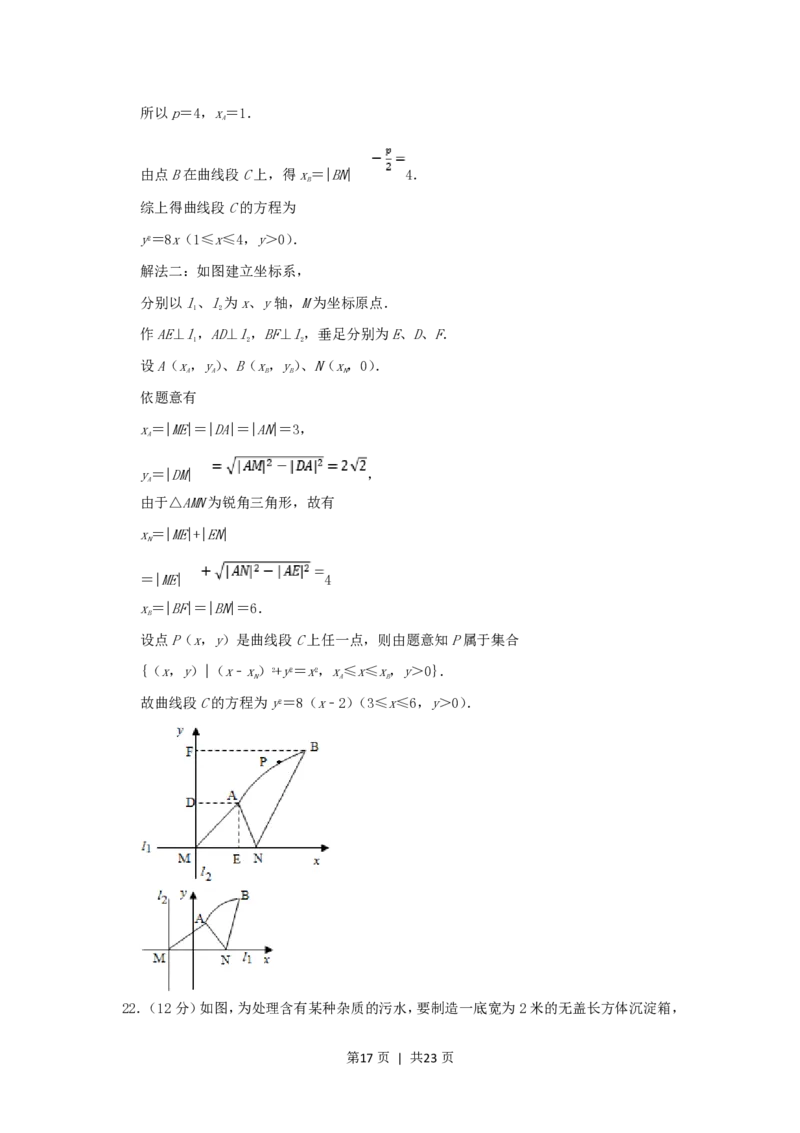
21.(12分)如图,直线l和l相交于点M,l⊥l,点N∈l.以A,B为端点的曲线段C
1 2 1 2 1
上的任一点到l的距离与到点N的距离相等.若△AMN为锐角三角形,|AM| ,|AN|
2
=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
22.(12分)如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,
第4页 | 共23页污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出
的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b
各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不
计).
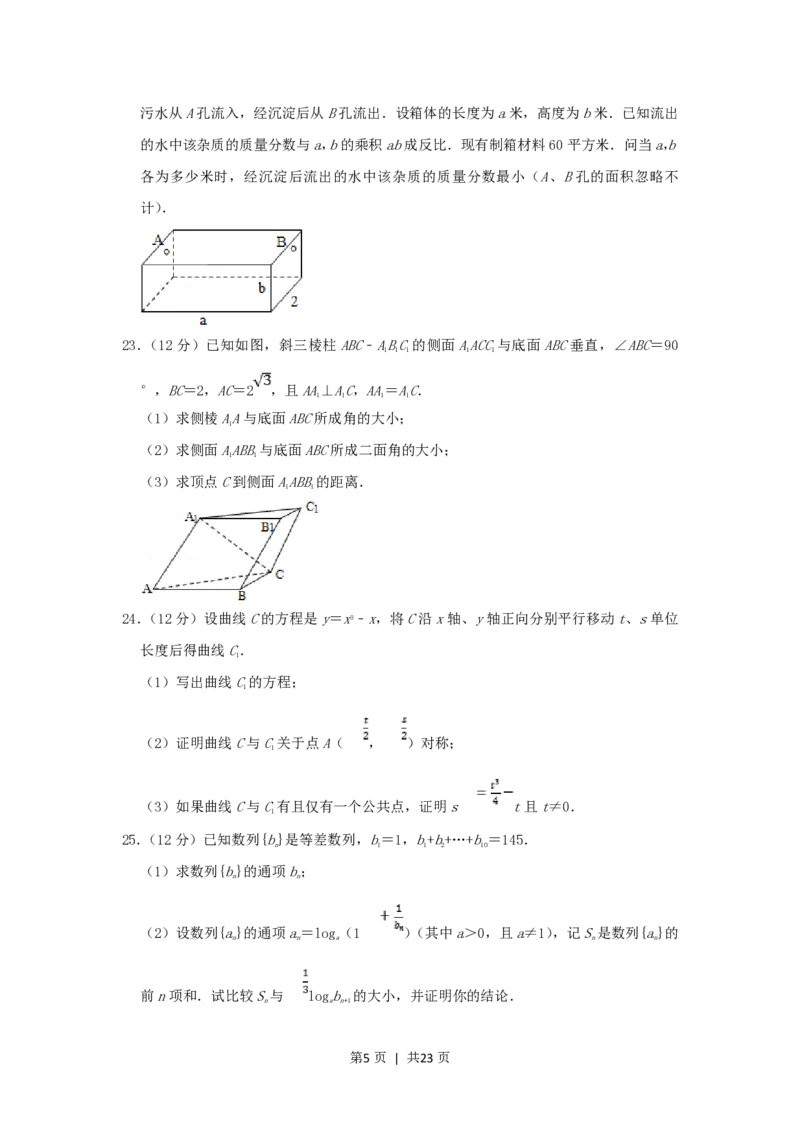
23.(12分)已知如图,斜三棱柱ABC﹣ABC的侧面AACC与底面ABC垂直,∠ABC=90
1 1 1 1 1
°,BC=2,AC=2 ,且AA⊥AC,AA=AC.
1 1 1 1
(1)求侧棱AA与底面ABC所成角的大小;
1
(2)求侧面AABB与底面ABC所成二面角的大小;
1 1
(3)求顶点C到侧面AABB的距离.
1 1
24.(12分)设曲线C的方程是y=x3﹣x,将C沿x轴、y轴正向分别平行移动t、s单位
长度后得曲线C.
1
(1)写出曲线C的方程;
1
(2)证明曲线C与C关于点A( , )对称;
1
(3)如果曲线C与C有且仅有一个公共点,证明s t且t≠0.
1
25.(12分)已知数列{b}是等差数列,b=1,b+b+…+b=145.
n 1 1 2 10
(1)求数列{b}的通项b;
n n
(2)设数列{a}的通项a=log(1 )(其中a>0,且a≠1),记S是数列{a}的
n n a n n
前n项和.试比较S与 logb 的大小,并证明你的结论.
n a n+1
第5页 | 共23页1998年全国统一高考数学试卷(理科)
参考答案与试题解析
一、选择题(共15小题,每小题4分,满分60分)
1.(4分)sin330°等于( )
A. B. C. D.
【解答】解:∵
故选:B.
2.(4分)函数y=a|x|(a>1)的图象是( )
A. B.
C. D.
【解答】解:法一:由题设知 y ,
又a>1.由指数函数图象易知答案为B.
法二:因y=a|x|是偶函数,又a>1.
所以a|x|≥1,排除AC.当x≥0,y=ax,由指数函数图象知选B.
故选:B.
3.(4分)曲线的极坐标方程ρ=4cosθ化为直角坐标方程为( )
A.(x+2)2+y2=4 B.(x﹣2)2+y2=4
C.(x+4)2+y2=16 D.(x﹣4)2+y2=16
【解答】解:将原极坐标方程ρ=4cosθ,化为:
第6页 | 共23页ρ2=4ρcosθ,
化成直角坐标方程为:x2+y2﹣4x=0,
即y2+(x﹣2)2=4.
故选:B.
4.(4分)两条直线Ax+By+C=0,Ax+By+C=0垂直的充要条件是( )
1 1 1 2 2 2
A.AA+BB=0 B.AA﹣BB=0
1 2 1 2 1 2 1 2
C. D.
【解答】解:直线Ax+By+C=0的方向向量为(﹣B,A),直线Ax+By+C=0的方向
1 1 1 1 1 2 2 2
向量为(﹣B,A),
2 2
两条直线Ax+By+C=0,Ax+By+C=0垂直,就是两条直线的方向向量的数量积为0,
1 1 1 2 2 2
即:(﹣B,A)(﹣B,A)=0 可得AA+BB=0
1 1 2 2 1 2 1 2
故选:A.
5.(4分)函数f(x) ( x≠0)的反函数f﹣1(x)=( )
A.x(x≠0) B. (x≠0) C.﹣x(x≠0) D. (x≠0)
【解答】由y 得x 且y≠0,所以反函数f﹣1(x) 且x≠0 故选则B
6.(4分)若点P(sinα﹣cosα,tanα)在第一象限,则在[0,2π)内α的取值范围是
( )
A. * B.
C. D.
【 解 答 】 解 : ∵ ⇒ ⇒
第7页 | 共23页故选:B.
7.(4分)已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为
( )
A.120° B.150° C.180° D.240°
【解答】解:圆锥的全面积是底面积的3倍,那么母线和底面半径的比为2,
设圆锥底面半径为1,则圆锥母线长为2,圆锥的侧面展开图扇形的弧长是圆锥底面周
长为2π,
该圆锥的侧面展开图扇形的圆心角:π,即180°
故选:C.
8.(4分)复数﹣i的一个立方根是i,它的另外两个立方根是( )
A. i B. i C.± i D.± i
【解答】解:∵﹣i=cos isin ,其立方根是 cos isin ,
k∈0,1,2,
即 i, i, i,
故选:D.
9.(4分)如果棱台的两底面积分别是S,S′,中截面的面积是S,那么( )
0
A.2 B.S C.2S=S+S′
0 0
D.S2=2S'S
0
【解答】解:不妨设棱台为三棱台,设棱台的高为2r,上部三棱锥的高为a,
根据相似比的性质可得: ,可得:
消去r,可得2
故选:A.
第8页 | 共23页10.(4分)向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系如图,
那么水瓶的形状是图中的( )
A. B.
C. D.
【解答】解:如果水瓶形状是圆柱,V=πr2h,r不变,V是h的正比例函数,
其图象应该是过原点的直线,与已知图象不符.故D错;
由已知函数图可以看出,随着高度h的增加V也增加,但随h变大,
每单位高度的增加,体积V的增加量变小,图象上升趋势变缓,
其原因只能是瓶子平行底的截面的半径由底到顶逐渐变小.故A、C错.
故选:B.
11.(4分)3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名
第9页 | 共23页护士.不同的分配方法共有( )
A.90种 B.180种 C.270种 D.540种
【解答】解:三所学校依次选医生、护士,不同的分配方法共有:C1C2C1C2=540种.
3 6 2 4
故选:D.
12.(4分)椭圆 1的焦点为F和F,点P在椭圆上,如果线段PF的中点在y轴上,
1 2 1
那么|PF|是|PF|的( )
1 2
A.7倍 B.5倍 C.4倍 D.3倍
【解答】解:由题设知F(﹣3,0),F(3,0),
1 2
如图,设P点的坐标是(x,y),线段PF 的中点坐标为( , )
1
∵线段PF的中点M在y轴上,
1
∴ 0
∴x=3
将P(3,y)代入椭圆 1,得到y2 .
∴|PF| ,
1
|PF| .
2
∴ .
故选:A.
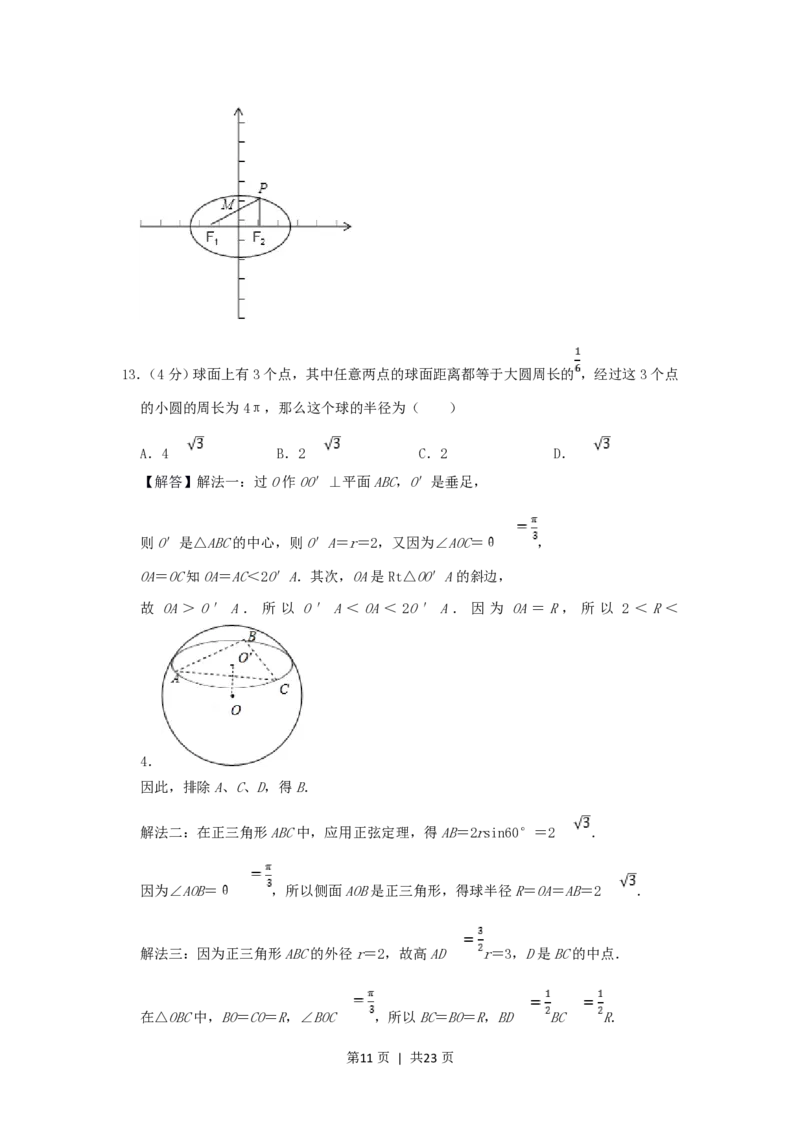
第10页 | 共23页13.(4分)球面上有3个点,其中任意两点的球面距离都等于大圆周长的 ,经过这3个点
的小圆的周长为4π,那么这个球的半径为( )
A.4 B.2 C.2 D.
【解答】解法一:过O作OO′⊥平面ABC,O′是垂足,
则O′是△ABC的中心,则O′A=r=2,又因为∠AOC=θ ,
OA=OC知OA=AC<2O′A.其次,OA是Rt△OO′A的斜边,
故 OA>O′A. 所 以 O′A<OA< 2O′A. 因 为 OA=R, 所 以 2 <R<
4.
因此,排除A、C、D,得B.
解法二:在正三角形ABC中,应用正弦定理,得AB=2rsin60°=2 .
因为∠AOB=θ ,所以侧面AOB是正三角形,得球半径R=OA=AB=2 .
解法三:因为正三角形ABC的外径r=2,故高AD r=3,D是BC的中点.
在△OBC中,BO=CO=R,∠BOC ,所以BC=BO=R,BD BC R.
第11页 | 共23页在Rt△ABD中,AB=BC=R,所以由AB2=BD2+AD2,得R2 R2+9,所以R=2 .
故选:B.
14.(4分)一个直角三角形三内角的正弦值成等比数列,其最小内角是( )
A.arccos B.arcsin C.arccos D.arcsin
【解答】解:设Rt△ABC中,C ,则A与B互余且A为最小内角.
又由已知得sin2B=sinA,即cos2A=sinA,1﹣sin2A=sinA,
解得sinA 或sinA (舍).
故选:B.
15.(4分)在等比数列{a}中,a>1,且前n项和S满足 S ,那么a的取值范围
n 1 n n 1
是( )
A.(1,+∞) B.(1,4) C.(1,2) D.(1, )
【解答】解:由题意知 S ,
n
∴a2=1﹣q,
1
∵a>1,|q|<1,∴1<a2<2,
1 1
∴ .
故选:D.
二、填空题(共4小题,每小题5分,满分20分)
16.(5分)已知圆C过双曲线 1的一个顶点和一个焦点,且圆心在此双曲线上,则
圆心到双曲线中心的距离是 .
【解答】解:由双曲线的几何性质易知圆C过双曲线同一支上的顶点和焦点,
所以圆C的圆心的横坐标为4.
第12页 | 共23页故圆心坐标为(4,± ).
∴它到中心(0,0)的距离为d .
故答案为: .
17.(5分)(x+2)10(x2﹣1)的展开式中x10的系数为 179 (用数字作答).
【解答】解:(x+2)10(x2﹣1)=x2(x+2)10﹣(x+2)10
∴(x+2)10(x2﹣1)的展开式中x10的系数是(x+2)10展开式的x8的系数﹣x10的系数
∵(x+2)10展开式的通项为T =Crx10﹣r2r=2rCrx10﹣r
r+1 10 10
∴令r=0,2分别得x10,x8的系数为1,180
故展开式中x10的系数为180﹣1=179,
故答案为179
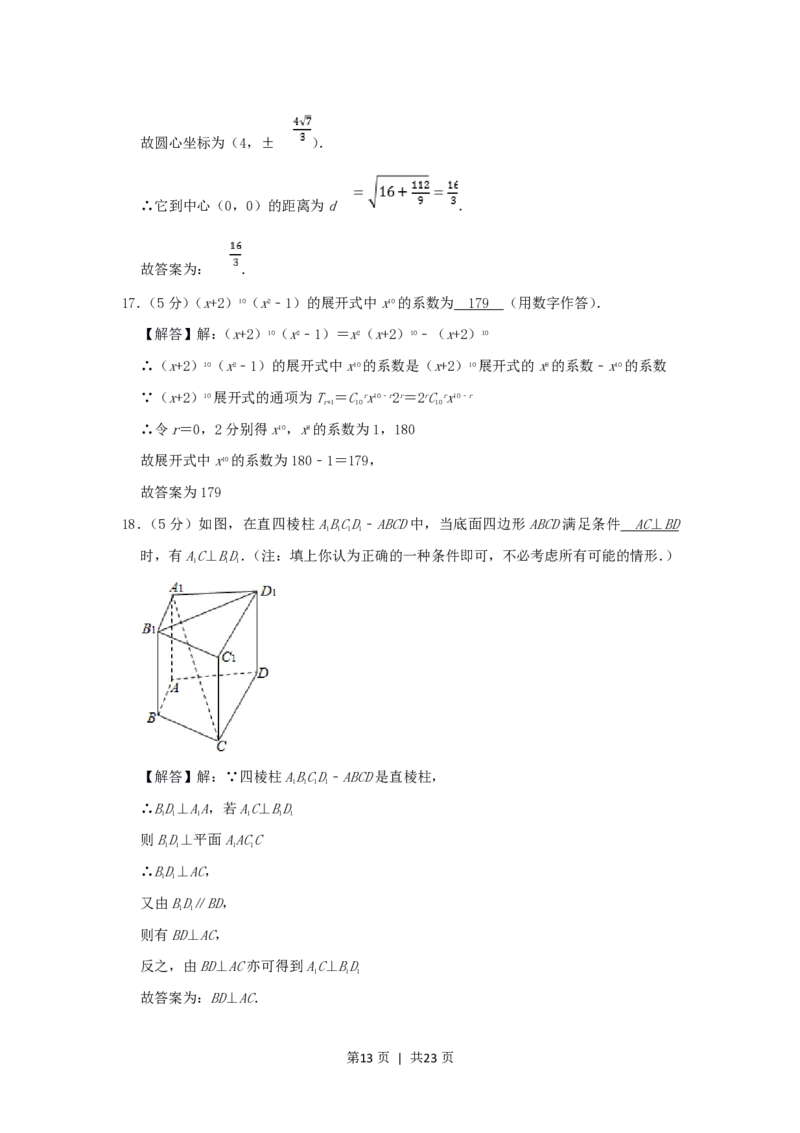
18.(5分)如图,在直四棱柱ABCD﹣ABCD中,当底面四边形ABCD满足条件 AC⊥BD
1 1 1 1
时,有AC⊥BD.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
1 1 1
【解答】解:∵四棱柱ABCD﹣ABCD是直棱柱,
1 1 1 1
∴BD⊥AA,若AC⊥BD
1 1 1 1 1 1
则BD⊥平面AACC
1 1 1 1
∴BD⊥AC,
1 1
又由BD∥BD,
1 1
则有BD⊥AC,
反之,由BD⊥AC亦可得到AC⊥BD
1 1 1
故答案为:BD⊥AC.
第13页 | 共23页19.(5分)关于函数f(x)=4sin (x∈R),有下列命题:
①由f(x)=f(x)=0可得x﹣x必是π的整数倍;
1 2 1 2
②y=f(x)的表达式可改写为y=4cos ;
③y=f(x)的图象关于点 对称;
④y=f(x)的图象关于直线x 对称.
其中正确的命题的序号是 ② .(把你认为正确的命题序号都填上)
【解答】解:函数f(x)=4sin 的最小正周期T=π,
由相邻两个零点的横坐标间的距离是 知①错.
利用诱导公式得f(x)=4cos
=4cos 4cos ,知②正确.
由于曲线f(x)与x轴的每个交点都是它的对称中心,
将x 代入得f(x)=4sin 0,
因此点( ,0)不是f(x)图象的一个对称中心,
故命题③错误.
曲线f(x)的对称轴必经过图象的最高点或最低点,且与y轴平行,而x 时y=
0,点
( ,0)不是最高点也不是最低点,
第14页 | 共23页故直线x 不是图象的对称轴,因此命题④不正确.
故答案为:②
三、解答题(共6小题,满分70分)
20.(10分)在△ABC中,a,b,c分别是角A,B,C的对边,设a+c=2b,A﹣C .求sinB
的值.以下公式供解题时参考:
sinθ+sin∅=2sin cos ,
sinθ﹣sin∅=2cos sin ,
cosθ+cos∅=2cos cos ,
cosθ﹣cos∅=﹣2sin sin .
【解答】解:由正弦定理和已知条件a+c=2b得sinA+sinC=2sinB.
由和差化积公式得2sin cos 2sinB.
由A+B+C=π得sin cos ,
又A﹣C 得 cos sinB,
所以 cos 2sin cos .
因为0 ,cos 0,
所以sin ,
第15页 | 共23页从而cos
所以sinB .
21.(12分)如图,直线l和l相交于点M,l⊥l,点N∈l.以A,B为端点的曲线段C
1 2 1 2 1
上的任一点到l的距离与到点N的距离相等.若△AMN为锐角三角形,|AM| ,|AN|
2
=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
【解答】解:法一:如图建立坐标系,
以l为x轴,MN的垂直平分线为y轴,点O为坐标原点.
1
依题意知:曲线段C是以点N为焦点,以l为准线的抛物线的一段,其中A,B分别为C
2
的端点.
设曲线段C的方程为
y2=2px(p>0),(x≤x≤x,y>0),
A B
其中x,x分别为A,B的横坐标,p=|MN|.
A B
所以M( ,0),N( ,0).
由|AM| ,|AN|=3得
(x )2+2px=17,①
A A
(x )2+2px=9.②
A A
由①,②两式联立解得x .再将其代入①式并由p>0解得
A
因为△AMN是锐角三角形,所以 x,故舍去
A
第16页 | 共23页所以p=4,x=1.
A
由点B在曲线段C上,得x=|BN| 4.
B
综上得曲线段C的方程为
y2=8x(1≤x≤4,y>0).
解法二:如图建立坐标系,
分别以l、l为x、y轴,M为坐标原点.
1 2
作AE⊥l,AD⊥l,BF⊥l,垂足分别为E、D、F.
1 2 2
设A(x,y)、B(x,y)、N(x,0).
A A B B N
依题意有
x=|ME|=|DA|=|AN|=3,
A
y=|DM| ,
A
由于△AMN为锐角三角形,故有
x=|ME|+|EN|
N
=|ME| 4
x=|BF|=|BN|=6.
B
设点P(x,y)是曲线段C上任一点,则由题意知P属于集合
{(x,y)|(x﹣x)2+y2=x2,x≤x≤x,y>0}.
N A B
故曲线段C的方程为y2=8(x﹣2)(3≤x≤6,y>0).
22.(12分)如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,
第17页 | 共23页污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出
的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b
各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不
计).
【解答】解法一:设y为流出的水中杂质的质量分数,
则y ,其中k>0为比例系数.依题意,即所求的a,b值使y值最小.
根据题设,有4b+2ab+2a=60(a>0,b>0),
得b (0<a<30).①
于是y
,
当a+2 时取等号,y达到最小值.
这时a=6,a=﹣10(舍去).
将a=6代入①式得b=3.
故当a为6米,b为3米时,经沉淀后流出的水中该杂质的质量分数最小.
解法二:依题意,即所求的a,b的值使ab最大.
由题设知4b+2ab+2a=60(a>0,b>0),
即a+2b+ab=30(a>0,b>0).
因为a+2b≥2 ,
第18页 | 共23页所以 ab≤30,
当且仅当a=2b时,上式取等号.
由a>0,b>0,解得0<ab≤18.
即当a=2b时,ab取得最大值,其最大值为18.
所以2b2=18.解得b=3,a=6.
故当a为6米,b为3米时,经沉淀后流出的水中该杂质的质量分数最小.
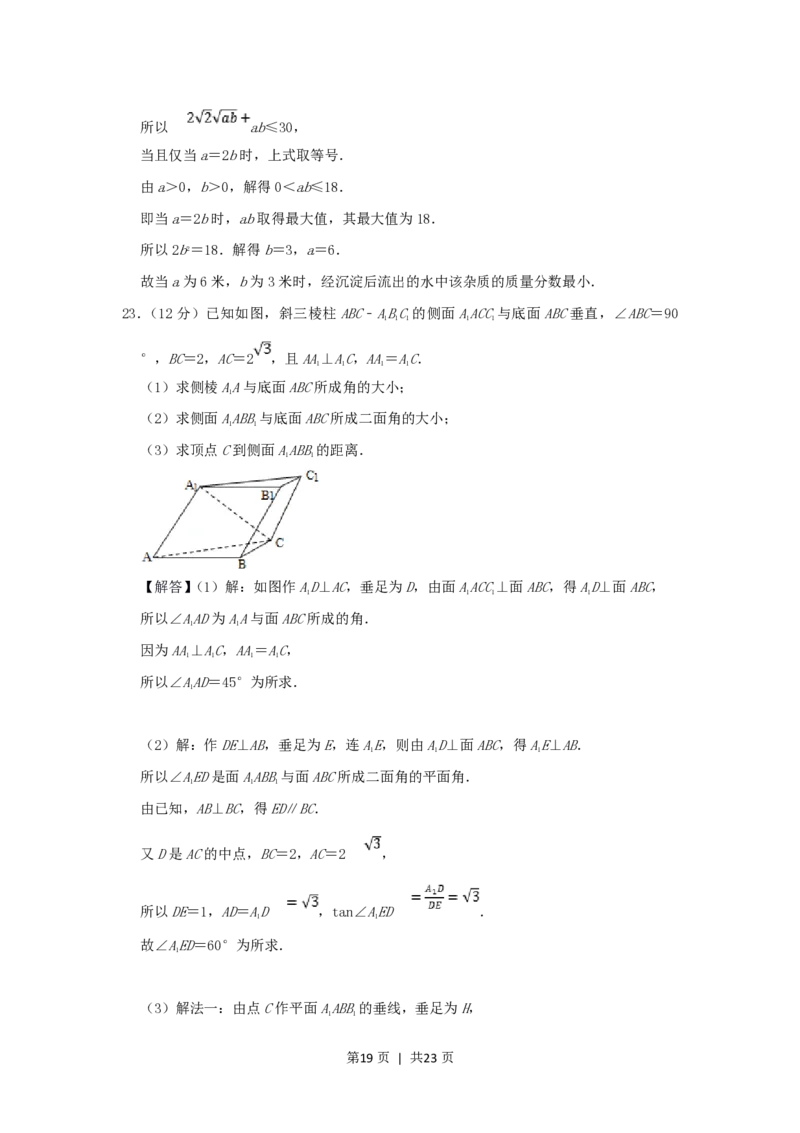
23.(12分)已知如图,斜三棱柱ABC﹣ABC的侧面AACC与底面ABC垂直,∠ABC=90
1 1 1 1 1
°,BC=2,AC=2 ,且AA⊥AC,AA=AC.
1 1 1 1
(1)求侧棱AA与底面ABC所成角的大小;
1
(2)求侧面AABB与底面ABC所成二面角的大小;
1 1
(3)求顶点C到侧面AABB的距离.
1 1
【解答】(1)解:如图作AD⊥AC,垂足为D,由面AACC⊥面ABC,得AD⊥面ABC,
1 1 1 1
所以∠AAD为AA与面ABC所成的角.
1 1
因为AA⊥AC,AA=AC,
1 1 1 1
所以∠AAD=45°为所求.
1
(2)解:作DE⊥AB,垂足为E,连AE,则由AD⊥面ABC,得AE⊥AB.
1 1 1
所以∠AED是面AABB与面ABC所成二面角的平面角.
1 1 1
由已知,AB⊥BC,得ED∥BC.
又D是AC的中点,BC=2,AC=2 ,
所以DE=1,AD=AD ,tan∠AED .
1 1
故∠AED=60°为所求.
1
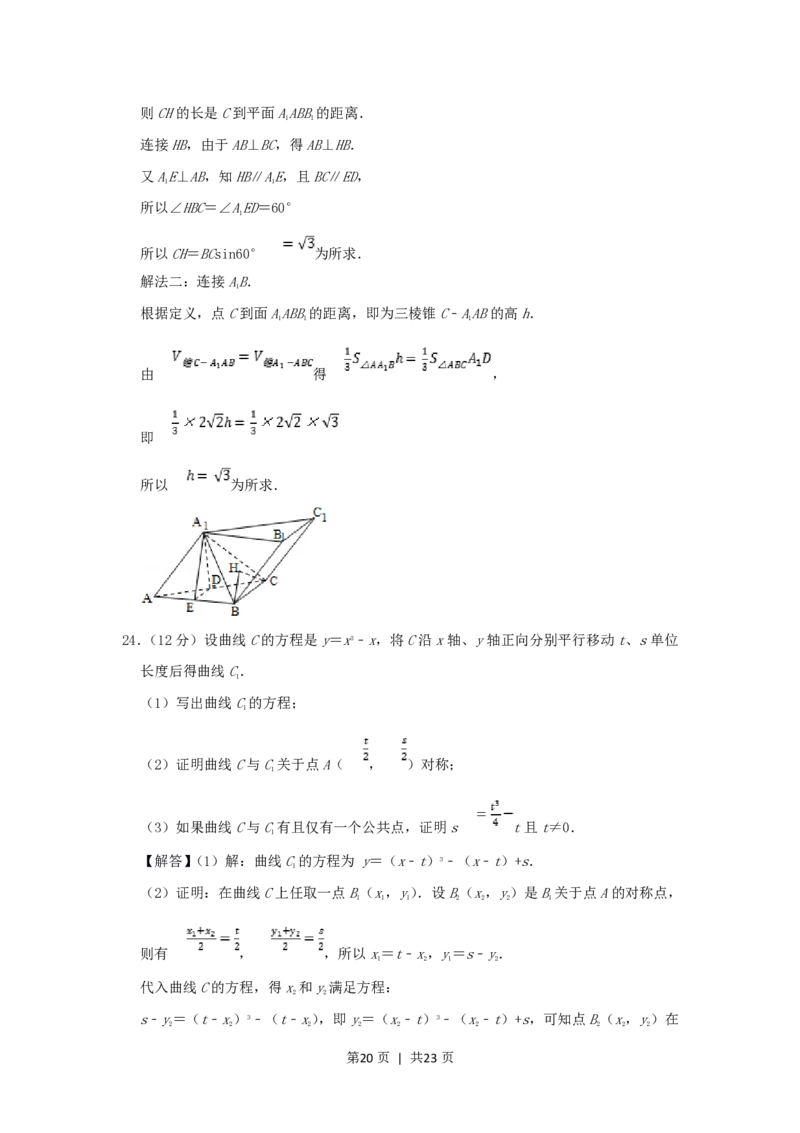
(3)解法一:由点C作平面AABB的垂线,垂足为H,
1 1
第19页 | 共23页则CH的长是C到平面AABB的距离.
1 1
连接HB,由于AB⊥BC,得AB⊥HB.
又AE⊥AB,知HB∥AE,且BC∥ED,
1 1
所以∠HBC=∠AED=60°
1
所以CH=BCsin60° 为所求.
解法二:连接AB.
1
根据定义,点C到面AABB的距离,即为三棱锥C﹣AAB的高h.
1 1 1
由 得 ,
即
所以 为所求.
24.(12分)设曲线C的方程是y=x3﹣x,将C沿x轴、y轴正向分别平行移动t、s单位
长度后得曲线C.
1
(1)写出曲线C的方程;
1
(2)证明曲线C与C关于点A( , )对称;
1
(3)如果曲线C与C有且仅有一个公共点,证明s t且t≠0.
1
【解答】(1)解:曲线C的方程为 y=(x﹣t)3﹣(x﹣t)+s.
1
(2)证明:在曲线C上任取一点B(x,y).设B(x,y)是B关于点A的对称点,
1 1 1 2 2 2 1
则有 , ,所以x=t﹣x,y=s﹣y.
1 2 1 2
代入曲线C的方程,得x和y满足方程:
2 2
s﹣y=(t﹣x)3﹣(t﹣x),即y=(x﹣t)3﹣(x﹣t)+s,可知点B(x,y)在
2 2 2 2 2 2 2 2 2
第20页 | 共23页曲线C上.
1
反过来,同样可以证明,在曲线C上的点关于点A的对称点在曲线C上.
1
因此,曲线C与C关于点A对称.
1
( 3 ) 证 明 : 因 为 曲 线 C与 C 有 且 仅 有 一 个 公 共 点 , 所 以 , 方 程 组
1
有且仅有一组解.
消去y,整理得 3tx2﹣3t2x+(t3﹣t﹣s)=0,这个关于x的一元二次方程有且仅有一个
根.
所以t≠0并且其根的判别式△=9t4﹣12t(t3﹣t﹣s)=0,即
所以 且t≠0.
25.(12分)已知数列{b}是等差数列,b=1,b+b+…+b=145.
n 1 1 2 10
(1)求数列{b}的通项b;
n n
(2)设数列{a}的通项a=log(1 )(其中a>0,且a≠1),记S是数列{a}的
n n a n n
前n项和.试比较S与 logb 的大小,并证明你的结论.
n a n+1
【解答】解:(1)设数列{b}的公差为d,由题意得
n
解得
所以b=3﹣2.
n n
(2)由b=3﹣2,知
n n
S=log(1+1)+log(1 )++log(1 )
n a a a
=log[(1+1)(1 )(1 )], logb =log .
a a n+1 a
第21页 | 共23页因此要比较 S 与 logb 的大小,可先比较(1+1)(1 )(1 )与
n a n+1
的大小.
取n=1有(1+1) ,
取n=2有(1+1)(1 ) ,
由此推测(1+1)(1 )(1 ) .①
若①式成立,则由对数函数性质可断定:
当a>1时,S logb .
n a n+1
当0<a<1时,S logb .
n a n+1
下面用数学归纳法证明①式.
(ⅰ)当n=1时已验证①式成立.
(ⅱ)假设当n=k(k≥1)时,①式成立,即
(1+1)(1 )(1 ) .
那么,当n=k+1时,
(1+1)(1 )(1 )(1 ) (1 )
(3k+2).
因为 ,
所以 (3k+2) .
因而(1+1)(1 )(1 )(1 ) .
第22页 | 共23页这就是说①式当n=k+1时也成立.
由(ⅰ),(ⅱ)知①式对任何正整数n都成立.
由此证得:
当a>1时,S logb .
n a n+1
当0<a<1时,S logb .
n a n+1
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/8/12 0:35:12;用户:黄熠;邮箱:huangyi12388@163.com;学号:716378
第23页 | 共23页