安徽省皖江名校联盟2024届高三下学期4月模拟数学试题+答案_2024年4月_01按日期_14号_2024届安徽省皖江名校联盟高三下学期4月二模_安徽省皖江名校联盟2024届高三下学期4月二模试题数学

姓名___________ 座位号_________________________
（在此卷上答题无效）
数 学
本试卷共 4页，19题。全卷满分 150分，考试时间 120分钟。
考生注意事项：
1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴
在答题卡上的指定位置。
2．选择题的作答：每小题选出答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑。写
在试卷、草稿纸和答题卡上的非答题区域均无效。
3．非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿
纸和答题卡上的非答题区域均无效。
4．考试结束后，请将本试卷和答题卡一并上交。
一、选择题：本题共 8小题，每小题 5分，共 40分。在每小题给出的四个选项中，只有一
项是符合题目要求的。
2i
1．已知复数z  ，则z的共轭复数z （ ）
i
A．12i B．12i C．12i D．12i
2．已知集合A1,2,3，B  x xa  ，AI ð B A，则实数a的取值范围是（ ）
R
A．a1 B．a1 C．a3 D．a3
3．已知m是直线，，是两个不同的平面，下列正确的命题是（ ）
A．若m∥，∥，则m∥ B．若m，，则m∥
C．若m∥，，则m D．若m∥，m，则
4．已知数列a 的前n项和为S n2 1，等比数列b 满足b a ，b a ，若b a ，则m
n n n 1 2 2 5 10 m
（ ）
310 1 310 1 39 1 39 1
A． B． C． D．
2 2 2 2
n
 2
5．已知 x  的展开式二项式系数和为256，则展开式中系数最大的项为（ ）
 x
A．第5项 B．第6项 C．第7项 D．第8项
1
6．已知函数 f x ax1 2（a 0且a 1）有两个零点，则实数a的取值范围是（ ）
a
 1 1 
A． 0,  B． ,1  C．0,1 D．1,
 2 2 
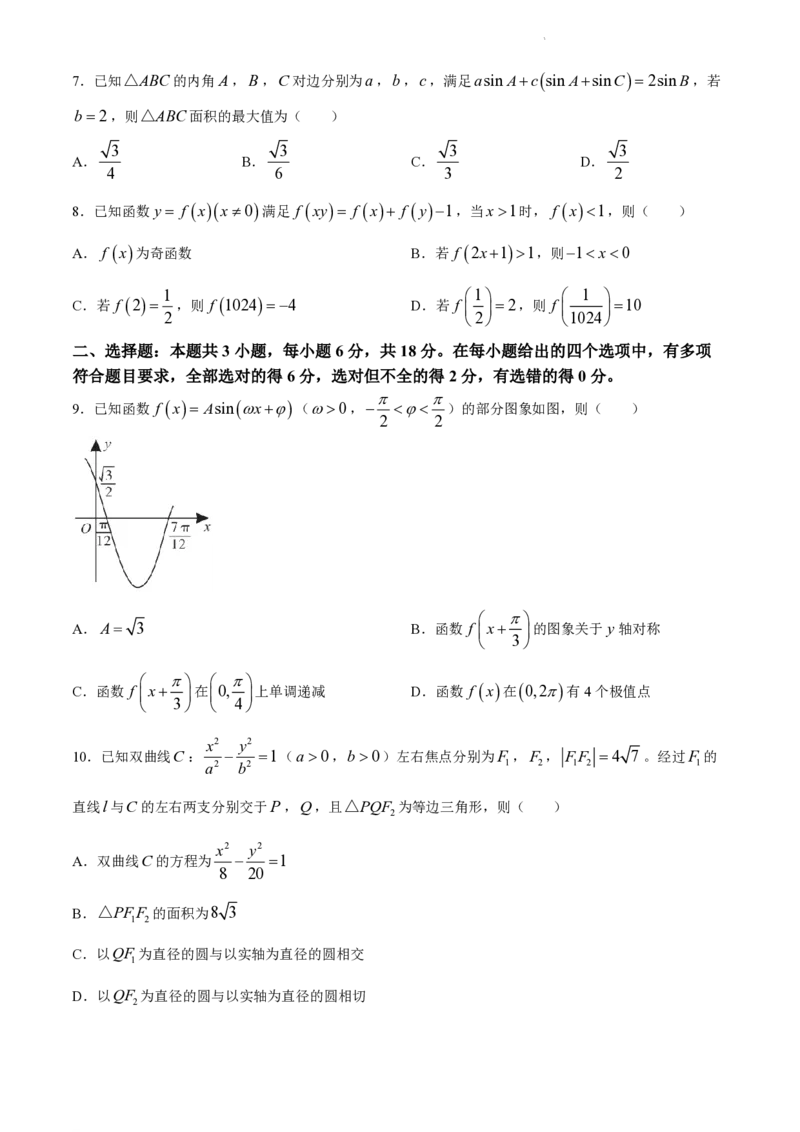
学科网（北京）股份有限公司7．已知△ABC的内角A，B，C对边分别为a，b，c，满足asin Acsin AsinC2sinB，若
b2，则△ABC面积的最大值为（ ）
3 3 3 3
A． B． C． D．
4 6 3 2
8．已知函数y  f xx0满足 f xy f x f y1，当x1时， f x1，则（ ）
A． f x为奇函数 B．若 f 2x11，则1 x0
1 1  1 
C．若 f 2 ，则 f 10244 D．若 f   2，则 f   10
2 2 1024
二、选择题：本题共 3小题，每小题 6分，共 18分。在每小题给出的四个选项中，有多项
符合题目要求，全部选对的得 6分，选对但不全的得 2分，有选错的得 0分。
 
9．已知函数 f x Asinx（0，  ）的部分图象如图，则（ ）
2 2
 
A．A 3 B．函数 f  x 的图象关于y轴对称
 3 
   
C．函数 f  x 在 0, 上单调递减 D．函数 f x在0,2有4个极值点
 3   4 
x2 y2
10．已知双曲线C：  1（a 0，b0）左右焦点分别为F ，F ， FF 4 7 。经过F 的
a2 b2 1 2 1 2 1
直线l与C的左右两支分别交于P，Q，且△PQF 为等边三角形，则（ ）
2
x2 y2
A．双曲线C的方程为  1
8 20
B．△PFF 的面积为8 3
1 2
C．以QF 为直径的圆与以实轴为直径的圆相交
1
D．以QF 为直径的圆与以实轴为直径的圆相切
2
学科网（北京）股份有限公司11．已知正方体ABCDABC D 的棱长为1，P，Q分别为棱C D ，BC上的动点，则（ ）
1 1 1 1 1 1 1
A．四面体PQAB的体积为定值 B．四面体PQAD的体积为定值
1
1 1
C．四面体PQAC的体积最大值为 D．四面体PQAD的体积最大值为
3 6
三、填空题：本题共 3小题，每小题 5分，共 15分。
12．一组样本10，16，20，12，35，14，30，24，40，43的第80百分位数是________．
13．已知抛物线y ax2的焦点F ，直线l过F 与抛物线交于A，B两点，若A4,4，则直线l的方程
为________，△OAB的面积为________（O为坐标原点）．
14．已知函数 f xx1sinxx1cosx，当0,时 f x的最大值与最小值的和为________．
四、解答题：共 77分。解答应写出文字说明、证明过程或演算步骤。
15．（13分）
已知函数 f x x2 10x3f1lnx．
（1）求函数 f x在点  1, f 1 处的切线方程；
（2）求 f x的单调区间和极值．
16．（15分）
为发展体育运动增强学生体质，甲乙两班各选3名同学进行乒乓球单打比赛，3场比赛每人参加一场比
赛，各场比赛互不影响，每场比赛胜者本班获得相应积分，负者班级积分为0。据统计可知甲班3名参赛
学生的情况如下表：
学生 A B C
获胜概率 0.4 0.6 0.8
获胜积分 6 5 4
（1）求甲班至少获胜2场的概率；
（2）记甲班获得积分为X ，求X 的分布列与数学期望．
17．（15分）
将正方形ABCD绕直线AB逆时针旋转90，使得CD到EF 的位置，得到如图所示的几何体．
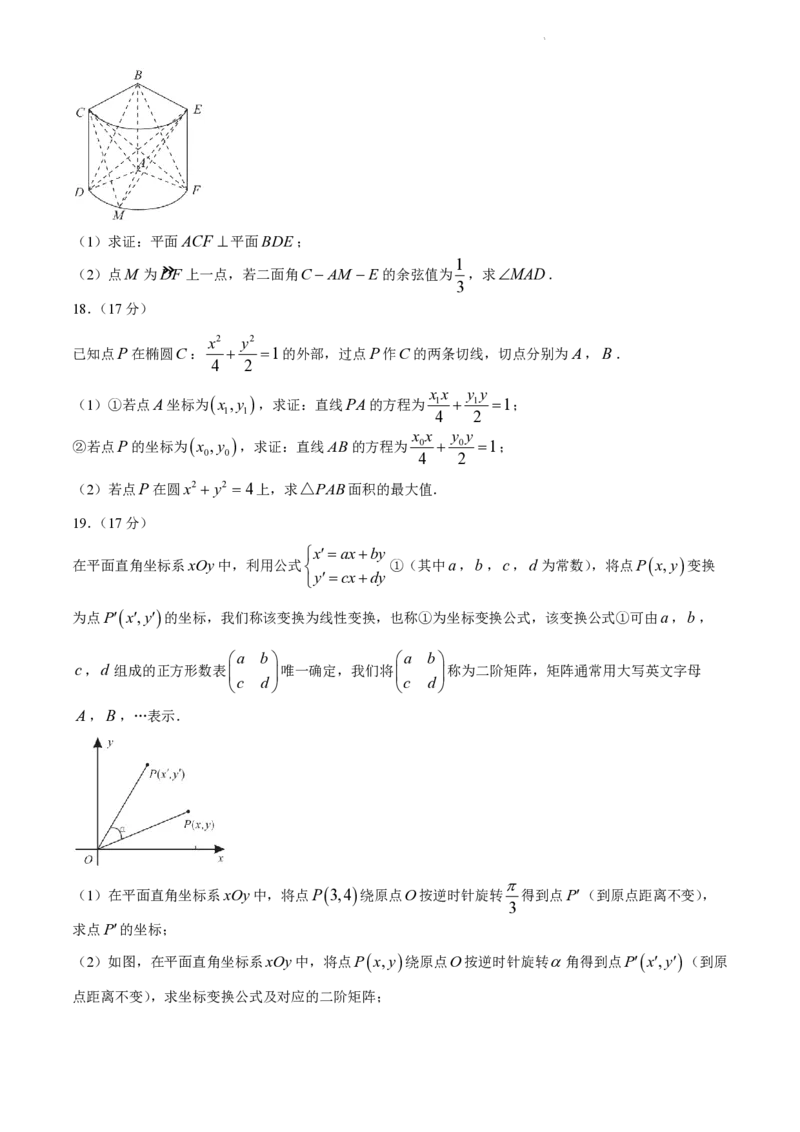
学科网（北京）股份有限公司（1）求证：平面ACF 平面BDE；
1
»
（2）点M 为DF上一点，若二面角CAM E的余弦值为 ，求MAD．
3
18．（17分）
x2 y2
已知点P在椭圆C：  1的外部，过点P作C的两条切线，切点分别为A，B．
4 2
x x y y
（1）①若点A坐标为x ,y ，求证：直线PA的方程为 1  1 1；
1 1 4 2
x x y y
②若点P的坐标为x ,y ，求证：直线AB的方程为 0  0 1；
0 0 4 2
（2）若点P在圆x2  y2 4上，求△PAB面积的最大值．
19．（17分）
xaxby
在平面直角坐标系xOy中，利用公式 ①（其中a，b，c，d 为常数），将点Px,y变换
ycxdy
为点Px,y的坐标，我们称该变换为线性变换，也称①为坐标变换公式，该变换公式①可由a，b，
a b a b
c，d 组成的正方形数表 唯一确定，我们将 称为二阶矩阵，矩阵通常用大写英文字母
c d c d
A，B，…表示．

（1）在平面直角坐标系xOy中，将点P3,4绕原点O按逆时针旋转 得到点P（到原点距离不变），
3
求点P的坐标；
（2）如图，在平面直角坐标系xOy中，将点Px,y绕原点O按逆时针旋转角得到点Px,y（到原
点距离不变），求坐标变换公式及对应的二阶矩阵；
学科网（北京）股份有限公司uuur x
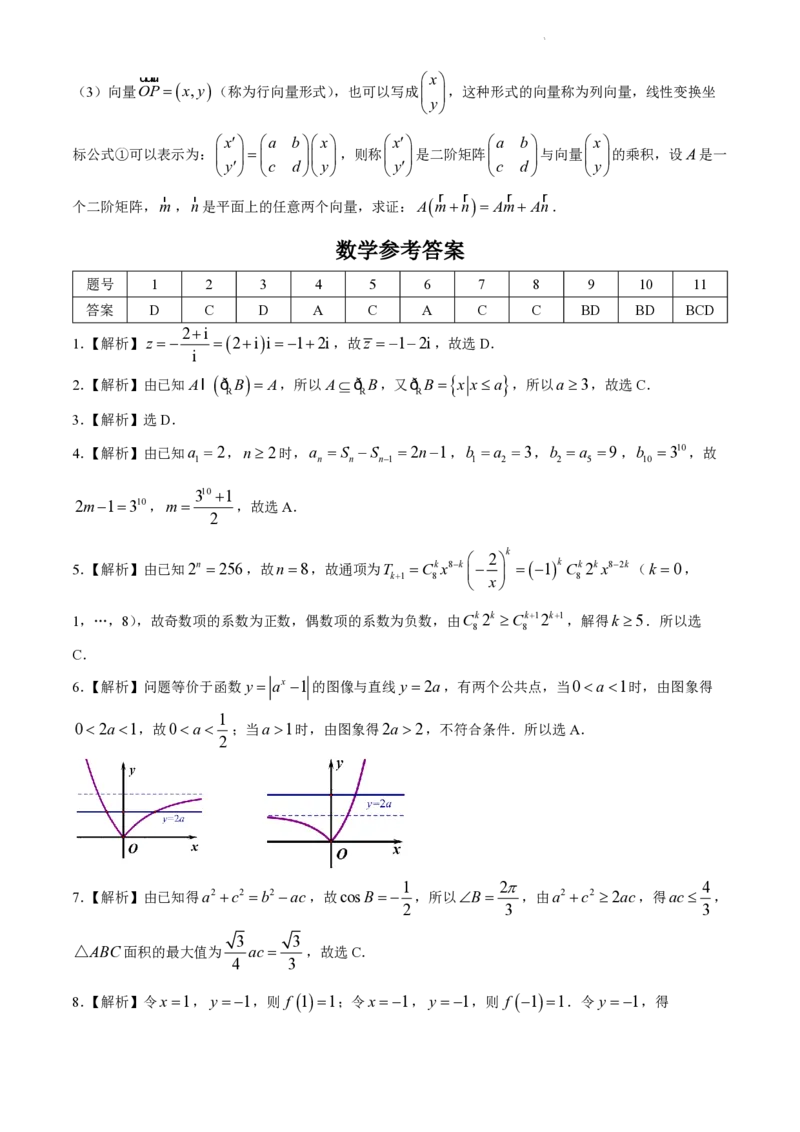
（3）向量OPx,y（称为行向量形式），也可以写成 ，这种形式的向量称为列向量，线性变换坐
y
x a bx x a b x
标公式①可以表示为：     ，则称 是二阶矩阵 与向量 的乘积，设A是一
y c dy y c d y
r r r r r r
个二阶矩阵，m，n是平面上的任意两个向量，求证：Amn Am An．
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D C D A C A C C BD BD BCD
2i
1．【解析】z  2ii12i，故z 12i，故选D．
i
2．【解析】由已知AI ð B A，所以Að B，又ð B  x xa  ，所以a3，故选C．
R R R
3．【解析】选D．
4．【解析】由已知a 2，n2时，a S S 2n1，b a 3，b a 9，b 310，故
1 n n n1 1 2 2 5 10
310 1
2m1310，m ，故选A．
2
k
 2
5．【解析】由已知2n 256，故n8，故通项为T Ckx8k



1k Ck2kx82k（k 0，
k1 8  x 8
1，…，8），故奇数项的系数为正数，偶数项的系数为负数，由Ck2k Ck12k1，解得k 5．所以选
8 8
C．
6．【解析】问题等价于函数y  ax 1的图像与直线y 2a，有两个公共点，当0a1时，由图象得
1
02a1，故0a ；当a 1时，由图象得2a 2，不符合条件．所以选A．
2
1 2 4
7．【解析】由已知得a2 c2 b2 ac，故cosB ，所以B ，由a2 c2 2ac，得ac ，
2 3 3
3 3
△ABC面积的最大值为 ac ，故选C．
4 3
8．【解析】令x1，y 1，则 f 11；令x1，y 1，则 f 11．令y 1，得
学科网（北京）股份有限公司x
f x f x，故y  f xx0为偶函数．任取x ，x 0,，x  x ，则 2 1，
1 2 1 2 x
1
 x 
则 f x  f x  f  2 1 f x ，故y  f xx0在0,上为减函数．由已知
1 2 x 2
 
1
1 1
f 2x11，可得 f  2x1   f 1，故 2x1 1，解得1 x0，且x ．若 f 2 ，
2 2
则 f 1024 f  210  f  29  f 2110f 294，故选C．
7  2
9．【解析】由图可知 f x的周期为：T 2    ，又T  ，所以2；
12 12 
     
由 f   0，sin    0，且  ，所以 ；
12  6  2 2 6
3  
由 f 0 ，所以A 3，故A错误；所以 f x 3sin  2x 
2  6 
   
因为 f  x  2sin  2x  2cos2x为偶函数，B正确；
 3   2 
       
x  0, ，则2x  0, ，故 f  x 在 0, 上单调递增，C错误；
 4   2   3   4 
 5 4 11
因为 f    3， f    3， f    3， f    3，故D正确。所以选BD。
 3   6   3   6 
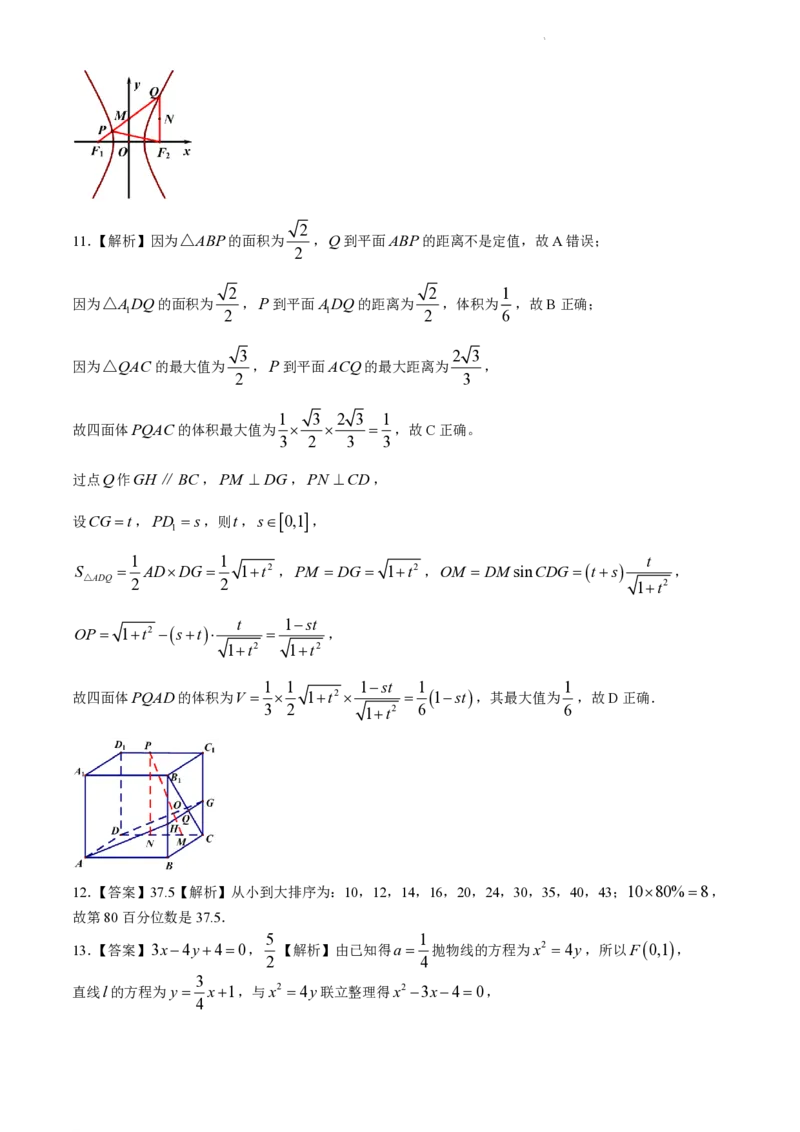
10．【解析】由已知得PQ PF QF ，由双曲线定义知：PF QF QF 2a，
2 2 1 1 2
PF  PF 2a 4a，故QF 4a，QF 6a，
2 1 2 1
1
在△QFF 中，由余弦定理得：16a2 36a2 224a2 167，
1 2 2
x2 y2
解得：a2 4，所以b2 24，方程为  1，A错误。
4 24
1 3
△PFF 的面积为S  8a2 8 3，B正确。
1 2 2 2
1 1 1
取QF 的中点M ，OM  QF  QF 2a QF a，两圆内切，故C错误。
1 2 2 2 1 2 1
1 1 1
取QF 的中点N ，则ON  QF  QF 2a QF a，两圆外切，故D正确。
2 2 1 2 2 2 2
学科网（北京）股份有限公司2
11．【解析】因为△ABP的面积为 ，Q到平面ABP的距离不是定值，故A错误；
2
2 2 1
因为△ADQ的面积为 ，P到平面ADQ的距离为 ，体积为 ，故B正确；
1 2 1 2 6
3 2 3
因为△QAC 的最大值为 ，P到平面ACQ的最大距离为 ，
2 3
1 3 2 3 1
故四面体PQAC的体积最大值为    ，故C正确。
3 2 3 3
过点Q作GH∥BC，PM  DG，PN CD，
设CG t，PD s，则t，s0,1，
1
1 1 t
S  ADDG  1t2 ，PM  DG  1t2 ，OM  DM sinCDG ts ，
△ADQ 2 2 1t2
t 1st
OP 1t2 st  ，
1t2 1t2
1 1 1st 1 1
故四面体PQAD的体积为V   1t2   1st，其最大值为 ，故D正确．
3 2 1t2 6 6
12．【答案】37.5【解析】从小到大排序为：10，12，14，16，20，24，30，35，40，43；1080%8，
故第80百分位数是37.5．
5 1
13．【答案】3x4y40， 【解析】由已知得a 抛物线的方程为x2 4y，所以F0,1，
2 4
3
直线l的方程为y  x1，与x2 4y联立整理得x2 3x40，
4
学科网（北京）股份有限公司1 5
故x 4，x 1，故△OAB的面积为S  OF   x  x   ．
1 2 2 1 2 2
 2 
14．【答案】 11【解析】
 
4
 
fxsinxx1cosxcosxx1sinx xcosxsinx，
   
当x  0, 时， fx0， f x递增；当x  , 时， fx0， f x递减；
 4   4 
 2
f x  f    ， f 01， f 1， f x 1
max  4  4 min
 2 
故最大值与最小值的和为： 11．
 
4
 
3f1
15．【解析】（1）由已知 fx2x10 ，
x
所以 f183f1，解得 f14，故 f x x2 10x12lnx， f 19
所求切线方程为：y94x1，即y 4x13
（2）由已知函数 f x x2 10x12lnx，定义域为0,
12 2  x2 5x6 
fx2x10  ，
x x
由 fx0，解得x2或x3
随x的变化 fx和 f x的变化如下
x 0,2 2 2,3 3 3,
fx
＋ 0 － 0 ＋
f x 单调递增 极大值 单调递减 极小值 单调递增
函数 f x单调递增区间为0,2和3,，单调递减区间为2,3
当x2时， f x取得极大值 f 21612ln2，
当x3时， f x取得极小值 f 32112ln3
16．【解析】（1）记A，B，C参赛获胜事件分别记为A，B，C表示，参赛失败分别记为A，B，
学科网（北京）股份有限公司C，
所以PA0.4，PB0.6，PC0.8，P  A  0.6，P  B  0.4，P  C  0.2
则甲班至少获胜2场事件记为M ，则M  ABC ABC ABC ABC
PM PABCP  ABC  P  ABC  P  ABC 
 PAPBPCPAPBP  C  PAP  B  PCP  A  PBPC
0.40.60.80.40.60.20.40.40.80.60.60.80.656
所以甲班至少获胜2场的概率为0.656
（2）由已知X 取值为0，4，5，6，9，10，11，15，
PX 0 P  ABC  0.60.40.20.048，PX 4 P  ABC  0.60.40.80.192，
PX 5 P  ABC  0.60.60.20.072，PX 6 P  ABC  0.40.40.20.032，
PX 9 P  ABC  0.60.60.80.288，PX 10 P  ABC  0.40.40.80.128，
PX 11 P  ABC  0.40.60.20.048，PX 15 PABC0.40.60.80.192，
所以
EX00.04840.19250.07260.03290.288100.128110.048150.192
0.7680.3600.1922.5921.2800.5282.8808.600
17．【解析】（1）由已知得平面ABCD平面ABEF，AF  AB，所以AF 平面ABCD
因为BD平面ABCD，故BD AF
因为ABCD是正方形，所以BD AC
AC，AF 平面ACF ，ACI AF  A，BD平面ACF
又BD平面BDE，所以平面ACF 平面BDE。
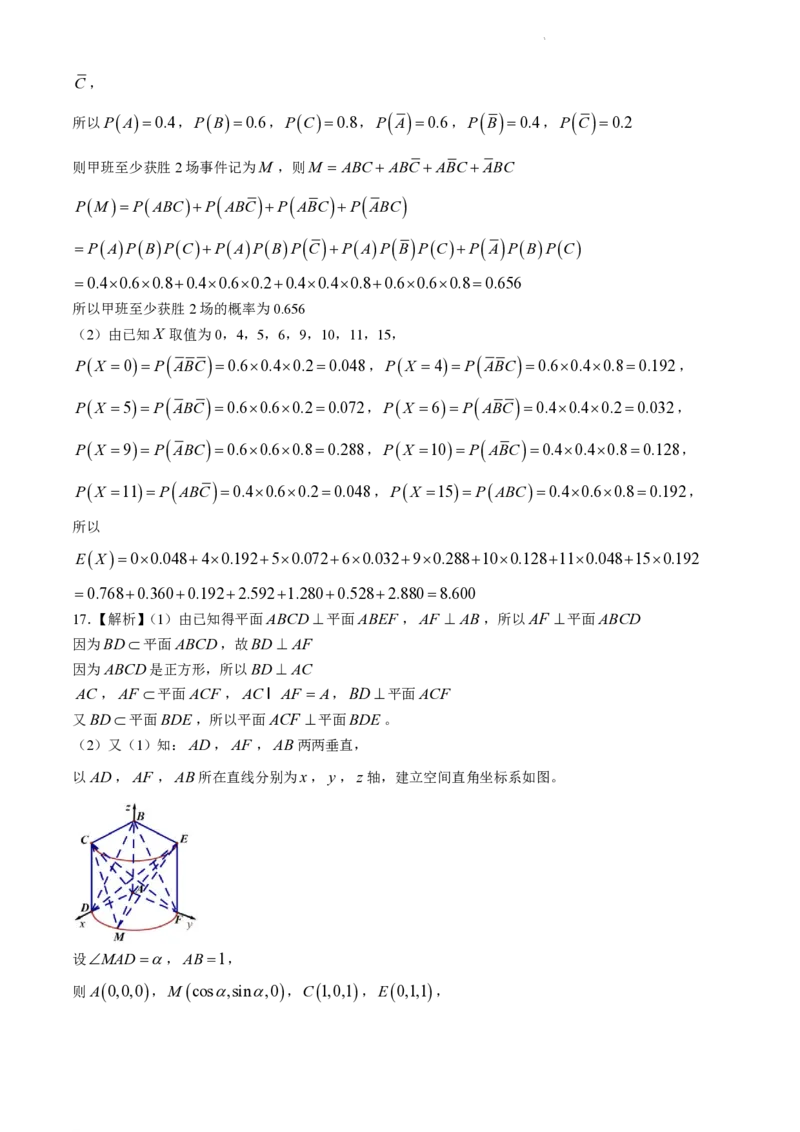
（2）又（1）知：AD，AF ，AB两两垂直，
以AD，AF ，AB所在直线分别为x，y，z轴，建立空间直角坐标系如图。
设MAD，AB1，
则A0,0,0，M cos,sin,0，C1,0,1，E0,1,1，
学科网（北京）股份有限公司uuuur uuur uuur
故AM cos,sin,0，AC 1,0,1，AE 0,1,1
r r uuur r uuuur
设平面AMC的法向量为mx ,y ,z ，则mAC 0，mAM 0
1 1 1
x z 0
故 1 1 ，取x sin，则y cos，z sin
x cos y sin0 1 1 1

1 1
r
所以msin,cos,sin
r r uuur r uuuur
设平面AME的法向量为n x ,y ,z ，nAE 0，nAM 0
2 2 2
y z 0
故 2 2 ，取x sin，则y cos，z cos
x cos y sin0 2 2 2

2 2
r
所以n sin,cos,cos
r r 1sincos
所以cos m,n  ，
1sin2 1cos2
1sincos 1
由已知得 
1sin2 1cos2 3
7
化简得：2sin229sin270，解得sin21或sin2 （舍去）
2
故45，即MAD45
18．【解析】（1）①当PA斜率存在时，y 0，设PA方程为：y y kxx 
1 1 1
x2 y2
与C：  1联立整理得：  12k2 x2 4ky kx x2y kx 2 40，
4 2 1 1 1 1
由已知得：16k2y kx 2 4  12k22y kx 2 4 0
1 1  1 1 
化简得：  4x2 k2 2x yk2 y2 0
1 1 1 1
因为x2 2y2 4，则4y2k2 4x ykx2 0，
1 1 1 1 1 1
x
即2ykx 2 0，所以k  1
1 1 2y
1
x
PA方程为：y y  1 xx ，即x x2y y  x2 2y2，
1 2y 1 1 1 1 1
1
x x y y
故直线PA的方程为 1  1 1
4 2
当PA斜率不存在时，y 0，直线PA的方程为x2或x2满足上式。
1
学科网（北京）股份有限公司x x y y
所以直线PA的方程为 1  1 1
4 2
x x y y
②由①知，设B点坐标为x ,y ，则直线PB的方程为 2  2 1
2 2 4 2
x x y y x x y y
由点P的坐标为x ,y ，则 1 0  1 0 1， 2 0  2 0 1，
0 0 4 2 4 2
x x y y
故直线AB的方程为 0  0 1
4 2
x x y y
（2）由（1）知直线AB的方程为 0  0 1，由题意知y 0，
4 2 0
x2 y2
与C：  1联立整理得：  x2 2y2 x2 8x x168y2 0
4 2 0 0 0 0
因为x2  y2 4，所以64x2 4  x2 2y2 168y2 32y2
0 0 0 0 0 0 0
8x 8x 168y2
因为Ax ,y ，Bx ,y ，则x x  0  0 ，x x  0
1 1 2 2 1 2 x2 2y2 y2 4 1 2 y2 4
0 0 0 0
 x2  43y2 32y4 2 y 2
 43y2
所以 AB  1 0  x x 2 4x x   0  0  0 0
 4y2   1 2 1 2 4y2  y2 4 2 y2 4
0 0 0
0
x2 2y2 4 y2
点P到直线AB的距离为：d  0 0  0
x2 4y2 43y2
0 0 0
3
1 2 y
所以△PAB面积S  AB d  0 y 0
2 y2 4 0
0
2y 3 2  y 4 12 
当0 y 2时，令 f y  0 ，所以 fy  0 0，
0 0 y2 4 0  y2 4 2
0
0
故 f y 在0,2单调递增，所以 f y 的最大值为 f 2 2
0 0
由对称性可知△PAB面积的最大值为 2
3 4
19．【解析】（1）可求得OPOP5，设POx，则cos ，sin ，
5 5

设点Px,y，POx ，
3
  1 3  3
故x5cos



5

cos sin

 2 3
 3   2 2  2
  1 3  3 3
y5sin



5

sin cos

2
 3   2 2  2
学科网（北京）股份有限公司3 3 3
所以P 2 3,2 
 
2 2
 
（2）设OPOPr，POx，则xrcos，y rsin，POx，
故xrcosrcoscosrsinsin xcos ysin
yrsinrsincosrcossin xsin ycos
x xcos ysin
所以坐标变换公式为
y xsin ycos
cos sin
该变换所对应的二阶矩阵为 
sin cos
a b r x  r x  r r x x 
（3）设矩阵A  ，向量m 1 ，n  2 ，则mn  1 2 ．
c d

y
 
y
 
y  y

1 2 1 2
r r a bx x  ax x by  y 
Amn   1 2  1 2 1 2 ，
c d y
1
 y
2  
cx
1
x
2
dy
1
 y
2


xax x by  y 
对应变换公式为： 1 2 1 2
 ycx
1
x
2
dy
1
 y
2

r a bx  ax by  r a bx  ax by 
Am   1  1 1 ，An    2  2 2 
c d y
 
cx dy

c d y
 
cx dy

1 1 1 2 2 2
r r ax by  ax by  ax x by  y 
所以Am An  1 1  2 2  1 2 1 2 
cx dy cx dy cx x dy  y 
 1 1   2 2   1 2 1 2 
xax x by  y 
故对应变换公式同样为 1 2 1 2
 ycx
1
x
2
dy
1
 y
2

r r r r
所以Amn Am An
学科网（北京）股份有限公司