文档内容
2000 年北京高考文科数学真题及答案
本试卷分第Ⅰ卷(选择题)和第卷(非选择题)两部分。第ⅠⅡ卷1至2页。第Ⅱ卷3至8页。
共150分。考试时间120分钟。
第Ⅰ卷(选择题共60分)
参考公式:
三角函数和差化积公式 正棱台、圆台的侧面积公式
inθ+sinΦ=2sin cos s - (c'+c)L
台侧
sinθ-sinΦ=2cos sin 其中c'、c分别表示、下底面周长,
L表
示棱高或母线长
cosθ+cosΦ=2cos cos 台体的体积公式 V = (S'+ +
台体
S)h
cosθ-cosΦ=-2sin sin 其中S'、S分别表示上、下底面积,h表示
高
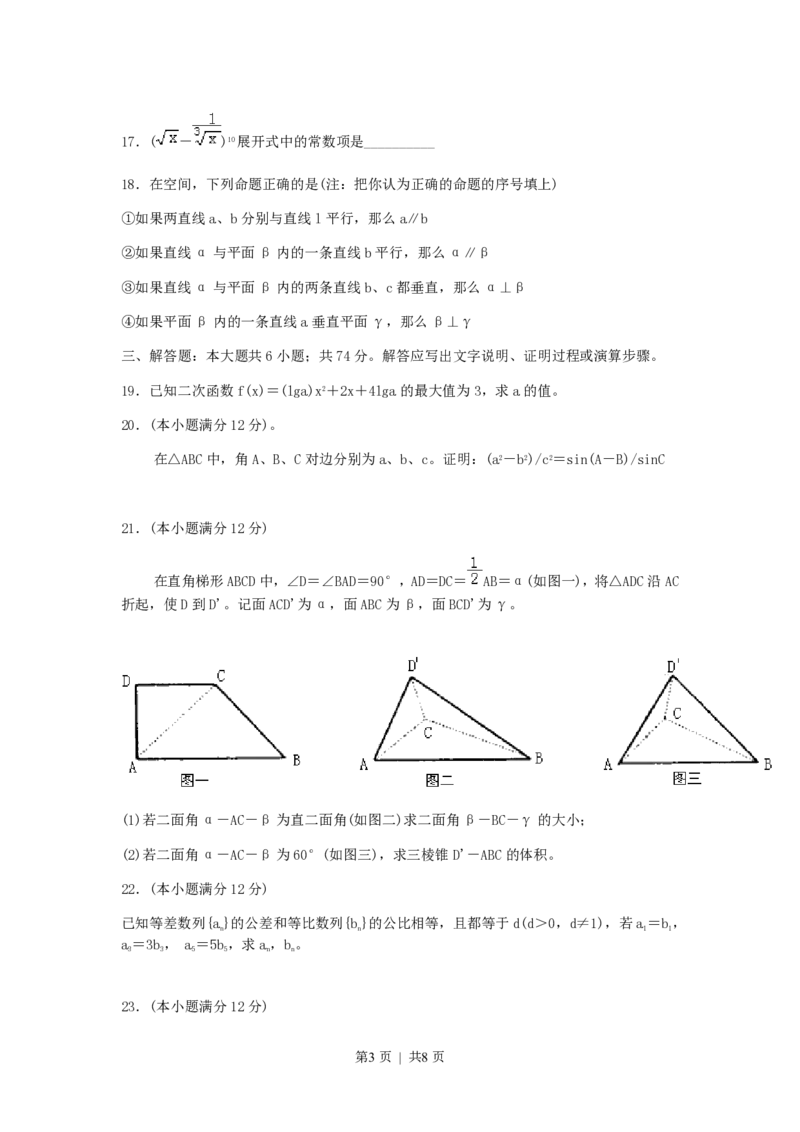
一、选择题:本大题共14小题;第(1)-(10)题每小题4分,第(11)-(14)题每小题5分,
共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数z=3+i,z=1-i,则z=zz 在复平面内的对应点位于
1 2 1 2
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设全集I={a,b,c,d,e},集合M={a,c,d},N={b,d,e},那么 ∩ 是
A.φ B.{d} C.{a,c} D.{b,e}
3.双曲线 =1的两条渐近线互相垂直,那么该双曲线的离心率是
A.2 B. C. D.3/2
4.下列方程的曲线关于x=y对称的是
A.x2-x+y2=1 B.x2y+xy2=1 C.x-y=1 D.x2-y2=1
5.一个圆锥的底面直径和高都同一个球的直径相等,那么圆锥的体积之比是
A.1∶3 B.2∶3 C.1∶2 D.2∶9
6.直线( - )x+y=3和直线x+( - )y=2的位置关系是
A.相交不垂直 B.垂直 C.平行 D.重合
7.函数y=lg|x|
A.是偶函数,在区间(-∞,0)上单调递增
B.是偶函数,在区间(-∞,0)上单调递减
C.是奇函数,在区间(0,+∞)上单调递增
D.是奇函数,在区间(0,+∞)上单调递减
8.从单词“equation”中选取5个不同的字母排成一排,含有“qu”(其中“qu”相连且顺
序不变)的不同排列共有
第1页 | 共8页A.120个 B.480个 C.720个 D.840个
9.椭圆短轴长2,长短是短轴的2倍,则椭圆中心到其准线的距离是
A.8/5 B.4/5 C.8/3 D.4/3
10.函数y=sinx+cosx+2 的最小值是
A.2- B.2+ C.0 D.1
11.设复数z=-1-i在复平面上对应向量 ,将 按顺时针方向旋转 π后得到向量
1
,令 对应的复数z 的辐角主值为θ,则tgθ=
2
A.2- B.-2+ C.2+ D.-2-
12.设α,β是一个钝角三角形的两个锐角,下列四个不等式中不正确的是
A.tgαtgβ<1 B.sinα+sinβ<
C.cosα+cosβ>1 D. tg(α+β)<(tgα+β)/2
13.已知等差数列{an}满足α+α+α+…+α =0则有
1 2 3 101
A.α+α >0 B.α+α <0 C.α+α =0 D.α =51
1 101 2 100 3 90 51
14.已知函数f(x)=ax3+bx2+cx+d的图象如右图,则
A.b∈(-∞,0) B.b∈(0,1)
C.b∈(1,2) D.b∈(2,+∞)
第Ⅱ卷(非选择题共90分)
二、填空题:本大题共4小题;每小题4分,共16分,把答案填在题中横线上。
15.函数y=cos(2π/3+ )的最小正周期是___________
16.右图是一体积为72的正四面体,连结两个面的重心E、F,则线段EF的长是_________
第2页 | 共8页17.( - )10展开式中的常数项是__________
18.在空间,下列命题正确的是(注:把你认为正确的命题的序号填上)
①如果两直线a、b分别与直线l平行,那么a∥b
②如果直线α与平面β内的一条直线b平行,那么α∥β
③如果直线α与平面β内的两条直线b、c都垂直,那么α⊥β
④如果平面β内的一条直线a垂直平面γ,那么β⊥γ
三、解答题:本大题共6小题;共74分。解答应写出文字说明、证明过程或演算步骤。
19.已知二次函数f(x)=(lga)x2+2x+4lga的最大值为3,求a的值。
20.(本小题满分12分)。
在△ABC中,角A、B、C对边分别为a、b、c。证明:(a2-b2)/c2=sin(A-B)/sinC
21.(本小题满分12分)
在直角梯形ABCD中,∠D=∠BAD=90°,AD=DC= AB=α(如图一),将△ADC沿AC
折起,使D到D'。记面ACD'为α,面ABC为β,面BCD'为γ。
(1)若二面角α-AC-β为直二面角(如图二)求二面角β-BC-γ的大小;
(2)若二面角α-AC-β为60°(如图三),求三棱锥D'-ABC的体积。
22.(本小题满分12分)
已知等差数列{a}的公差和等比数列{b}的公比相等,且都等于d(d>0,d≠1),若a=b,
n n 1 1
a=3b, a=5b,求a,b。
3 3 5 5 n n
23.(本小题满分12分)
第3页 | 共8页如图,设点A和B为抛物线y2=4x(p>0)上原点以外的两个动点。已知OA⊥OB,OM⊥AB。
求点M的轨迹方程,并说明它表示什么曲线。
24.(本小题满分12分)
某地区上年度电价为0.8元/kW·h,年用电量为akW.h。本年度计划将电价降到0.55年
/kW·h至0.75元/kW·h之间,而用户期望电价为0.4元/kW·h。经测算,下调电价后新增
的用电量与实际电价和用户期望电价的差成反比(比例系数为k)。该地区电力的成本价为
0.3元/kW·h
(1)写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式;
(2)设k=0.2a,当电价最低定为多少时仍可保证电部门的收益比上年至少增长20%?
(注:收益=实际用电量×(实际电价-成本价))
2000年普通高等到学校春季招生考试(北京、安徽卷)
数学试题(文史类)参考解答及评分标准
说明:
一、本解答指出了每题考查的主要知识和能力,并给出了一种或几种解法供参考。如果考生
的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则。
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容
和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;
如果后继部分的解答有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分。
一、选择题:本题考查基本知识的基本运算,第1—10题每小题4分,第11—14题每小题5
分,满分60分。
1、D 2、A 3、C 4、B 5、C
6、B 7、B 8、B 9、D 10、A
11、C 12、D 13、C 14、A
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分。
第4页 | 共8页15、3 16、2 17、-252 18、① ,④
三、解答题
19.本小题主要考查二次函数最大值和最小值的概念,以及对于配方法、对数方程、
二次方程的解法的运用能力。满分12分。
解:原函数可化成
f(x)=lga(x+ )2- +4lga …………4分
由已知,f(x)有最大值3,所以lga<0,并且
- +4lga=3
整理得 4(lga)2-3lga-1=0 …………8分
解得 lga=1,lga=-1/4 …………10分
∵ lga<0
故取 lga=-1/4
∴ a= = …………12分
20.本小题主要考查三角形的正弦定理、余弦定理等基础知识,考查三角函数简单的
变形技能。满分12分。
证明:由余弦定理 a2=b2+c2-2bccosA
b2=a2+c2-2accosB …………3分
∴ a2-b2=b2-a2-2bccosA+2accosB
整理得 = …………6分
依正弦定理,有 , …………9分
∴ =
= …………12分
21.本小题主要考查空间线面关系,及运算、推理、空间想象能力。(满分12分)
解:(1)在直角梯形ABCD中 由已知△DAC为等腰直角三角形,
第5页 | 共8页∴ AC= a , ∠CAB=45°
过C作CH⊥AB,由AB=2a 可推得AC=BC= a
∴
AC⊥BC …………2分
取AC的中点E,连结D'E, 则D'E⊥AC
又∵ 二面角α-AC-β为直二面角, ∴ D'E⊥β
又∵ BC 平面β ∴ BC⊥D'E
∴ BC⊥α,而D'C α ∴ BC⊥D'C …………4分
∴ ∠D'CA为二面角β-BC-γ的平面角
由于∠D'CA=45°
∴ 二面角β-BC-γ为45°。 …………6分
(2)取AC的中点E,连结D'E,再过D'作D'O⊥β,垂足为O,
连结OE。
∵ AC⊥D'E ∴ AC⊥OE
∴ ∠D'EO为二面角α-AC-β的平面角,
∴ ∠D'EO =
60° …………9分
在Rt△D'OE中,D'E=AC/2= a/2
∴ V =(1/3)S ·D'O =(1/3)×(1/2)AC·BC·D'O
D'-ABC △ABC
=(1/6)× a× a× a/4=( /12)a3 …………12分
22.本小题考查等差数列和等比数列的概念、性质,方程组的解法,以及运算能力和
分析能力。满分12分。
解:由已知
…………4分
由①得 a(3d2-1)=2d ③
1
由②得 a(5d4-1)=4d ④
1
因为 d≠0,由③式和④式得 2(3d2-1)=5d4-1
第6页 | 共8页即 5d4-6d2+1=0 …………7分
解得 d=±1,d=±
∵ d>0,d≠1,∴ d=
代入③,得 a=- ,故b=-
1 1
a=- + (n-1)= (n-6) …………10分
n
b=- × …………12分
1
23.本小题考查直线、抛物线的基础知识,考查由动点轨迹方程的基本方法以及方程
化简的基本技能。满分12分。
解:如图,点A,B在抛物线y2=4px上
设A( ,y),B( ,y),OA,OB的斜率分
A A
别为k 、k 。
OA OB
∴ k = = 4p/y , k =
OA A OB
4p/y …………2分
B
由 OA⊥OB,得 k ·k = =-1
OA OB
① …………4分
依点A在AB上,得直线AB方程
(y+y)(y-y)=4p(x- ) ② …………6分
A B A
由OM⊥AB,得直线OM方程 y= x ③…………8分
设点M(x,y),则x,y满足②、③现式,将②式两边同时乘以-x/4p,并利用③
式整理得
x. +yy-(x2+y2)=0 ④ …………10分
A
由③、④两式得 (-x/4p)yy-(x2+y2)=0
A B
由①式知 yy=-16p2 ∴ x2+y2-4px=0
A B
第7页 | 共8页因为A、B是原点以外的两点,所以x≠0。
所以点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原
点。…………12分
24.本小题主要考查建立函数关系、解不等式基础知识,考查综合应用数学知识、思
想和方法解决实际问题的能力,满分12分。
解:(1)设下调后的电价为x元/kW·h,依题意知用电量增至 +a,电力部门的
收益为
y=( +a)(x-0.3)(0.55≤x≤0.75)
(2)依题意有
整理得
解此不等式得 0.60≤x≤0.75
答:当电价最低定为0.60元/kW·h,仍可保证电力部门的收益比上年至少增长20%。
第8页 | 共8页