山东实验中学2024届高三下学期2月调研考试数学试卷(1)_2024年3月_013月合集_2024届新高考19题（九省联考模式）数学合集140套

山东省实验中学 2024 届高三调研考试 数学试题 2024.2 说明：本试卷满分 150分.试题答案请用 2B铅笔和 0.5mm签字笔填涂到答题卡规定位置上，书 写在试题上的答案无效.考试时间 120分钟. 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是符 合题目要求的 1.设A={ 1,4,2x } ,B= { 1,x2 } ，若B⊆ A，则x=（ ） A.0 B.0或2 C.0或-2 D.2或-2 n  2  2.若  x +  展开式中只有第6项的二项式系数最大，则n=（ ）  x2  A.9 B.10 C.11 D.12       3.已知向量a =( 1,3 ) ,b =( 2,2 )，则cos a+b,a−b =（ ） 1 17 5 2 5 A. B. C. D. 17 17 5 5 { } { } 4.等差数列 a 的首项为1，公差不为0.若a ,a ,a 成等比数列，则 a 前6项的和为（ ） n 2 3 6 n A.-24 B.-3 C.3 D.8  π 5.要得到函数y =cos2x的图象，只需将函数y =sin2x+ 的图象（ ）  3 π π A.向右平移 个单位 B.向左平移 个单位 6 6 π π C.向右平移 个单位 D.向左平移 个单位 12 12 1 2 6.在三棱锥P−ABC 中，线段PC上的点M 满足PM = PC，线段PB上的点N 满足PN = PB，则三 3 3 棱锥P−AMN 和三棱锥P−ABC的体积之比为（ ） 1 1 2 4 A. B. C. D. 9 3 9 9 7.为研究某池塘中水生植物的覆盖水塘面积x（单位：dm2）与水生植物的株数y（单位：株）之间的相关 关系，收集了4组数据，用模型y =cekx(c>0)去拟合x与y的关系，设z =lny,x与z的数据如表格所示： 得到x与z的线性回归方程zˆ =1.2x+aˆ，则c=（ ） 学科网（北京）股份有限公司x 3 4 6 7 z 2 2.5 4.5 7 A.-2 B.-1 C.e−2 D.e−1 x2 y2 8.双曲线M : − =1(a>0,b>0)的左､右顶点分别为A,B，曲线M 上的一点C关于x轴的对称点为 a2 b2 9 D，若直线AC的斜率为m，直线BD的斜率为n，则当 mn+ 取到最小值时，双曲线离心率为 mn （ ） A.3 B.4 C. 3 D.2 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的四个选项中，有多项符合题 目要求.全部选对的得6分，部分选对的得部分分，有选错的得 0分. 9.已知复数z满足z2 +z+1=0，则（ ） 1 3 A.z =− + i B. z =1 2 2 C.z2 = z D.z+z2 +z3++z2024 =0 10.过线段x+ y =4 ( 0x4 ) 上一点P作圆O:x2 + y2 =4的两条切线，切点分别为A,B，直线AB与x,y 轴分别交于点M,N ，则（ ） A.点O恒在以线段AB为直径的圆上 B.四边形PAOB面积的最小值为4 C. AB 的最小值为2 2 D. OM + ON 的最小值为4 ( ) 11.已知函数 f ( x )=ln x2 +1−x+1 ，则（ ） ( ) A. f x 在其定义域上是单调递减函数 B.y = f ( x ) 的图象关于 ( 0,1 ) 对称 C. f ( x ) 的值域是 ( 0,+∞) D.当x>0时， f ( x )− f (−x ) mx恒成立，则m的最大值为-1 学科网（北京）股份有限公司三､填空题：本题共 3小题，每小题 5分，共 15分. 12.已知随机变量X ∼B ( n, p ) .若E ( X )=30,D ( X )=20，则 p = __________. x2 y2 13.已知抛物线y2 =2px(p>0)的焦点F 为椭圆 + =1的右焦点，直线l过点F 交抛物线于A,B两 4 3 点，且 AB =8.直线l ,l 分别过点A,B且均与x轴平行，在直线l ,l 上分别取点M,N （M,N 均在点A,B 1 2 1 2 的右侧），∠ABN 和∠BAM 的角平分线相交于点P，则PAB的面积为__________. 14.已知正方体ABCD−ABC D 的棱长为2 3,M,N 为BD 的三等分点，动点P在ACB 内，且PMN 1 1 1 1 1 1 2 6 的面积为 ，则点P的轨迹长度为__________. 3 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 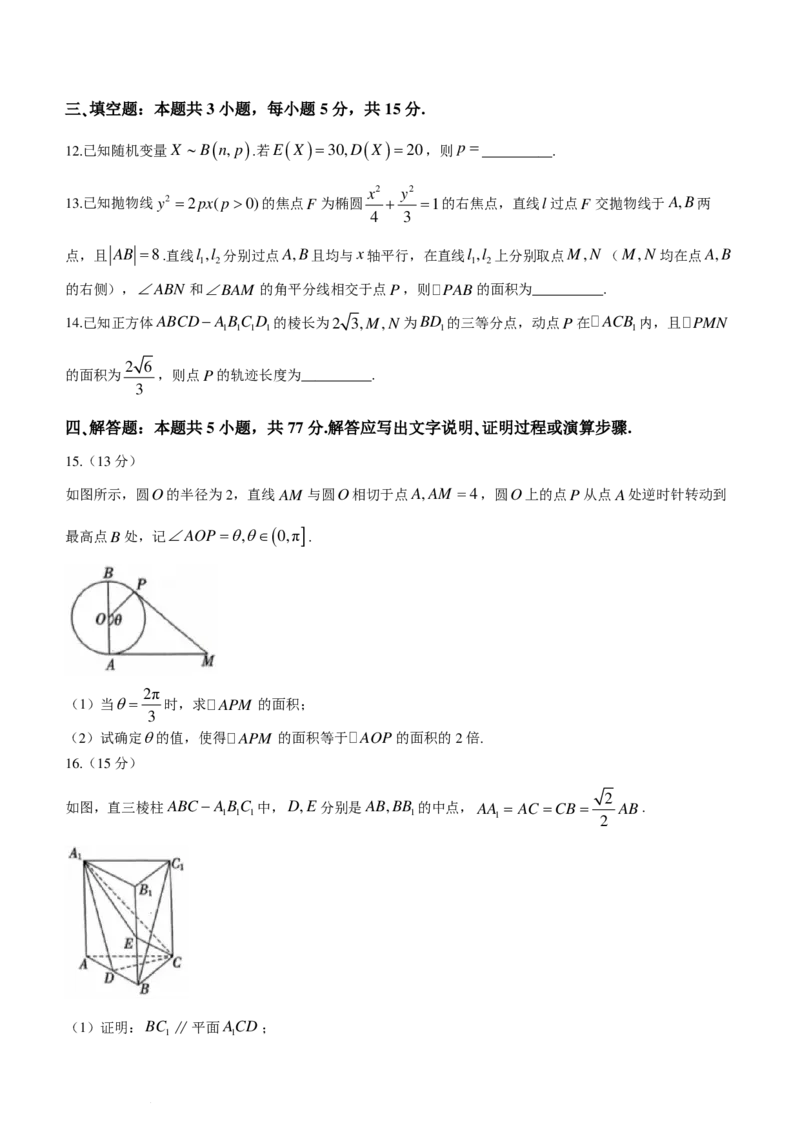15.（13分） 如图所示，圆O的半径为2，直线AM 与圆O相切于点A,AM =4，圆O上的点P从点A处逆时针转动到 最高点B处，记∠AOP=θ,θ∈( 0,π ] . 2π （1）当θ= 时，求APM 的面积； 3 （2）试确定θ的值，使得APM 的面积等于AOP的面积的2倍. 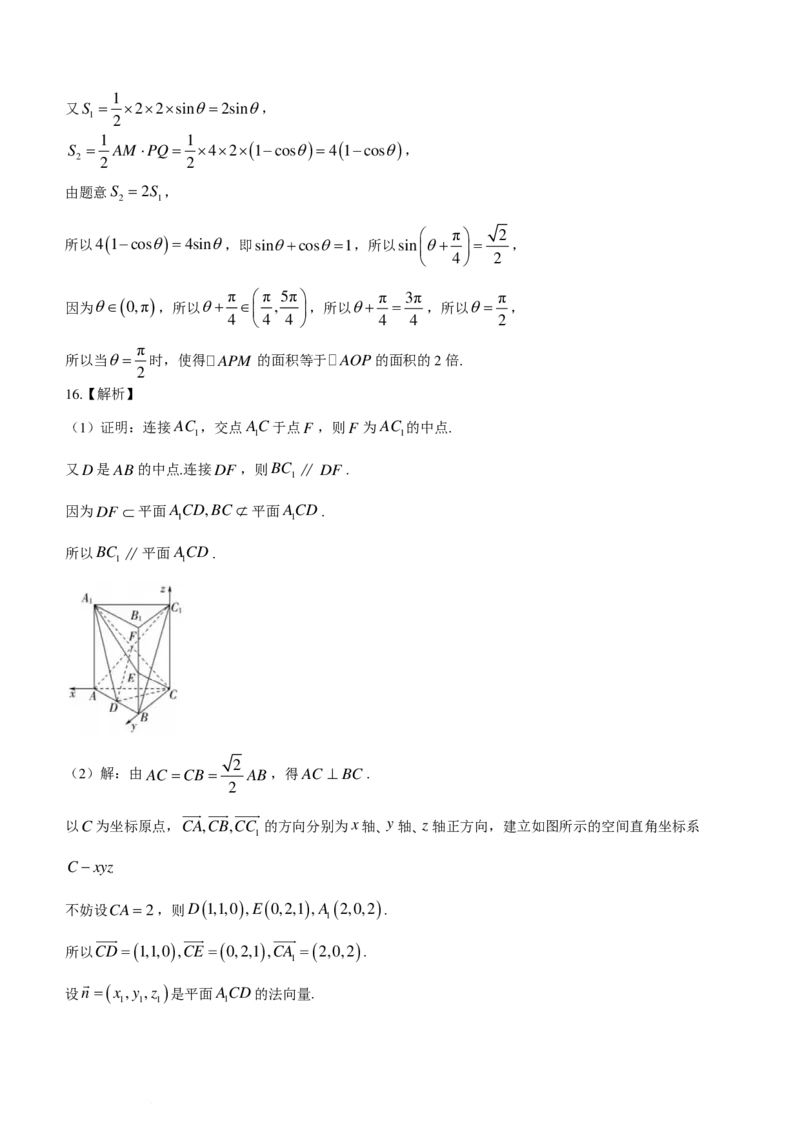16.（15分） 2 如图，直三棱柱ABC−ABC 中，D,E分别是AB,BB 的中点，AA = AC =CB= AB. 1 1 1 1 1 2 （1）证明：BC ∥平面ACD； 1 1 学科网（北京）股份有限公司（2）求二面角D−AC−E的正弦值. 1 17.（15分） 盒中有大小颜色相同的6个乒乓球，其中4个未使用过（称之为新球），2个使用过（称之为旧球）.每局比 赛从盒中随机取2个球作为比赛用球，比赛结束后放回盒中.使用过的球即成为旧球. （1）求一局比赛后盒中恰有3个新球的概率； （2）设两局比赛后盒中新球的个数为X ，求X 的分布列及数学期望. 18.（17分） 1 已知函数 f ( x )= x2 −alnx,a∈R, f′( x )是 f ( x ) 的导函数，g ( x )= xex . 2 ( ) （1）求 f x 的单调区间； ( ) （2）若 f x 有唯一零点. ①求实数a的取值范围； ②当a >0时，证明：g ( x )> f′( x )+4. 19.（17分） 已知有穷数列A:a ,a ,,a ( n3 ) 中的每一项都是不大于n的正整数.对于满足1mn的整数m，令集合 1 2 n A ( m )={ k∣a =m,k =1,2,,n } .记集合A ( m ) 中元素的个数为s ( m ) （约定空集的元素个数为0）. k ( ) ( ) （1）若A:6,3,2,5,3,7,5,5，求A 5 及s 5 ； 1 1 1 （2）若 + ++ =n，求证：a ,a ,,a 互不相同； s ( a ) s ( a ) s ( a ) 1 2 n 1 2 n （3）已知a =a,a =b，若对任意的正整数i, j ( i ≠ j,i+ jn ) 都有i+ j∈A ( a ) 或i+ j∈A ( a ) ，求 1 2 i j a +a ++a 的值. 1 2 n 学科网（北京）股份有限公司山东省实验中学 2024 届高三调研考试 数学参考答案 2024.2 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是符 合题目要求的. 题号 1 2 3 4 5 6 7 8 答案 C B B A D C C D 二､多选题：本题共 3小题，每小题 6分，共 18分，在每小题给出的四个选项中，有多项符合 题目要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分 题号 9 10 11 答案 BC BCD ACD 三､填空题：本题共 3小题，每小题 5分，共 15分 1 2 6π 12. 13.8 2 14. 3 3 四､解答题：共 77分.解答应写出文字说明､证明过程或演算步骤. 15.【解析】 （1）过点P作PQ⊥ AM 交AM 于点Q，如图： 因为圆O的半径为2， 2π 由题意PQ=2−2cosθ=2−2cos =3， 3 1 所以APM 的面积为 ×4×3=6 2 （2）连接AP，设AOP的面积为S ,APM 的面积为S ， 1 2 学科网（北京）股份有限公司1 又S = ×2×2×sinθ=2sinθ， 1 2 1 1 S = AM ⋅PQ= ×4×2×( 1−cosθ)=4 ( 1−cosθ)， 2 2 2 由题意S =2S ， 2 1  π 2 所以4 ( 1−cosθ)=4sinθ，即sinθ+cosθ=1，所以sin θ+  = ，  4 2 π π 5π π 3π π 因为θ∈( 0,π ) ，所以θ+ ∈  , ，所以θ+ = ，所以θ= ， 4 4 4  4 4 2 π 所以当θ= 时，使得APM 的面积等于AOP的面积的2倍. 2 16.【解析】 （1）证明：连接AC ，交点AC于点F ，则F 为AC 的中点. 1 1 1 又D是AB的中点.连接DF，则BC ∥ DF. 1 因为DF ⊂平面ACD,BC ⊄平面ACD. 1 1 所以BC ∥平面ACD. 1 1 2 （2）解：由AC =CB= AB，得AC ⊥ BC . 2    以C为坐标原点，CA,CB,CC 的方向分别为x轴､y轴､z轴正方向，建立如图所示的空间直角坐标系 1 C−xyz ( ) ( ) ( ) 不妨设CA=2，则D 1,1,0 ,E 0,2,1 ,A 2,0,2 . 1    所以CD=( 1,1,0 ) ,CE =( 0,2,1 ) ,CA =( 2,0,2 ) . 1  设n =( x ,y ,z ) 是平面ACD的法向量. 1 1 1 1 学科网（北京）股份有限公司   n⋅CD=0 x + y =0  则  ，即 1 1 ，取n =( 1,−1,−1 ) . n⋅CA 1 =0 2x 1 +2z 1 =0  同理，设m=( x ,y ,z ) 是平面ACE的法向量， 2 2 2 1    m⋅CE =0 2y +z =0  则  ，即 2 2 ，取m=( 2,1,−2 ) . m⋅CA 1 =0 2x 2 +2z 2 =0     n⋅m 3   6 从而cos n,m =   = ，故sin n,m = . n m 3 3 6 所以二面角D−AC−E的正弦值为 . 1 3 17.【解析】 C1C1 8 解答：（1）P= 2 4 = C2 15 6 （2）X 的可能取值为0,1,2,3,4. C2 C2 6 P ( X =0 )= 4 ⋅ 2 = ， C2 C2 225 6 6 C2 C1C1 C1C1 C2 72 P ( X =1 )= 4 ⋅ 4 2 + 4 2 ⋅ 3 = ， C2 C2 C2 C2 225 6 6 6 6 C2 C2 C1C1 C1C1 C2 C2 114 P ( X =2 )= 4 ⋅ 4 + 4 2 ⋅ 3 3 + 2 ⋅ 4 = ， C2 C2 C2 C2 C2 C2 225 6 6 6 6 6 6 C2 C1C1 C1C1 C2 32 P ( X =3 )= 2 ⋅ 4 2 + 4 2 ⋅ 3 = ， C2 C2 C2 C2 225 6 6 6 6 C2 C2 1 P ( X =4 )= 2 ⋅ 2 = ， C2 C2 225 6 6 所以X 的分布列为 X 0 1 2 3 4 6 72 114 32 1 P 225 225 225 225 225 6 72 114 32 1 16 E ( X )=0× +1× +2× +3× +4× = . 225 225 225 225 225 9 18.【解析】 学科网（北京）股份有限公司解：（1） f ( x ) 的定义域为( 0,+∞) , f′( x )= x− a = x2 −a ， x x 当a0时， f′( x )>0恒成立，故 f ( x ) 的单调递增区间是 ( 0,+∞) ，无单调递减区间； 当a >0时，令 f′( x )>0得x> a；令 f′( x )<0得0< x< a ； ( ) ( ) 所以 f ( x ) 单调递减区间为 0, a ；单调递增区间为 a,+∞ （2）①法一； ( ) 当a =0时， f x 没有零点，不符合题意； 当a<0时，函数 f ( x ) 在 ( 0,+∞) 单调递增， 1 1 因为 f ( x )= x2 −alnx< x2 −a ( x−1 )， 2 2 取m=a+ a2 −2a >0，则 f ( m )<0， 1 又 f ( 1 )= >0，故存在唯一x ∈( m,1 ) ，使得 f ( x )=0，符合题意； 0 0 2 （此处用极限说明也可以） ( ) 当a >0时，由（1）可知， f ( x ) 有唯一零点只需 f a =0， a a 即 − lna =0，解得a=e； 2 2 综上，a的取值范围为 (−∞,0 )∪{ e } . 法二： 当a =0时， f ( x ) 没有零点，不符合题意； 1 lnx 所以 f ( x )=0⇔ = ， 2a x2 lnx 1−2lnx 令ϕ( x )= ，则ϕ′( x )= ， x2 x3 ( ) 当x∈ 0, e 时，ϕ′( x )>0,ϕ( x ) 单调递增； ( ) 当x∈ e,+∞ 时，ϕ′( x )<0,ϕ( x ) 单调递减； 又 limϕ(x)=0 . x→+∞ 1 1 ( ) 1 所以 <0或 =ϕ e = ， 2a 2a 2e 即a<0或a=e， 综上，a的取值范围为 (−∞,0 )∪{ e } . 学科网（北京）股份有限公司②由①得出a=e，  1 令h ( x )= xex −2ex− (x>0)  2 h′( x )=( x+1 ) ex −2e， h′′( x )=( x+2 ) ex >0，所以h′( x ) 单调递增，又h′( 1 )=0， 故当x∈( 0,1 ) 时，h′( x )<0,h ( x ) 单调递减； 当x∈( 1,+∞) 时，h′( x )>0,h ( x ) 单调递增；  1 故h ( x ) h ( 1 )=0，故g ( x )= xex 2ex−   2  1 e 要证g ( x )> f′( x )+4，只需证明2ex−  > f′( x )+4= x− +4，  2 x 即证 ( 2e−1 ) x2 −( e+4 ) x+e>0， 9 5  9  5 由Δ=12e+16−7e2 =12e− e2 +16− e2 =e12− e +16− e2 2 2  2  2  9  5 0成立.故不等式得证. 19.【解析】 解：（1）因为a =a =a =5，所以A ( 5 )={ 4,7,8 } ，则s ( 5 )=3. 4 7 8 （2）依题意s ( a ) 1,i =1,2,,n， i 1 1 1 1 则有 1，因此 + ++ n， ( ) ( ) ( ) ( ) s a s a s a s a i 1 2 n 1 1 1 又因为 + ++ =n， ( ) ( ) ( ) s a s a s a 1 2 n 所以s ( a )=1，所以a ,a ,,a 互不相同. i 1 2 n （3）依题意a =a,a =b. 1 2 由i+ j∈A ( a ) 或i+ j∈A ( a ) ，知a =a 或a =a . i j i+j i i+j j 学科网（北京）股份有限公司令 j =1，可得a =a 或a =a ，对于i =2,3,,n−1成立， i+1 i i+1 1 故a =a 或a =a . 3 2 3 1 ①当a =b时，a =a ==a =a， 3 4 n 所以a +a ++a =na 1 2 n ②当a ≠b时，a =a或a =b. 3 3 当a =a时，由a =a 或a =a ，有a =a， 3 4 3 4 1 4 同理a =a ==a =a，所以a +a ++a =( n−1 ) a+b 5 6 n 1 2 n 当a =b时，此时有a =a =b， 3 2 3 令i =1, j =3，可得4∈A ( a ) 或4∈A ( b ) ，即a =a或a =b. 4 4 令i =1, j =4，可得5∈A ( a ) 或5∈A ( b ) .令i =2, j =3，可得5∈A ( b ) .所以a =b. 5 若a =a，则令i =1, j =4，可得a =a，与a =b矛盾.所以有a =b. 4 5 5 4 不妨设a =a ==a =b ( k5 ) , 2 3 k 令i =t, j =k+1−t ( t =2,3,,k−1 ) ，可得k+1∈A ( b ) ，因此a =b. k+1 令i =1, j =k ，则a =a或a =b.故a =b. k+1 k+1 k+1 所以a +a ++a =( n−1 ) b+a 1 2 n 综上，a =b时，a +a ++a =na. 1 2 n a =a≠b时，a +a ++a =( n−1 ) a+b. 3 1 2 n a =b≠a时，a +a ++a =( n−1 ) b+a. 3 1 2 n 学科网（北京）股份有限公司