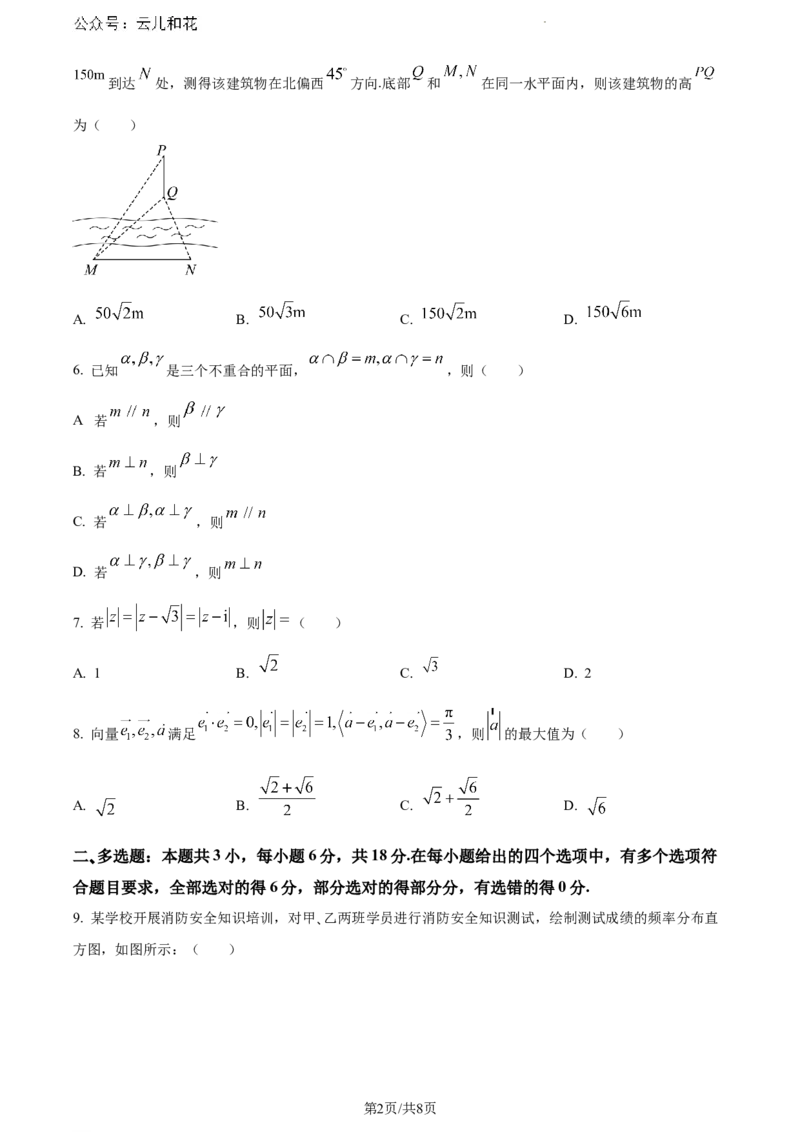文档内容
厦门市 2023—2024 学年第二学期高一期末质量检测
数学试题
满分:150分考试 时间:120分钟
考生注意:
1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的
条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将答题卡交回.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 若 ,则 ( )
A. B. C. D.
2. 为了解某校高一年级学生体育锻炼情况,用比例分配的分层随机抽样方法抽取50人作为样本,其中男
生20人.已知该校高一年级女生240人,则高一年级学生总数为( )
A. 600 B. 480 C. 400 D. 360
3. 在梯形 中 , , ,以 所在直线为旋转轴,其余各
边旋转一周形成的面所围成的几何体的体积为( )
.
A B. C. D.
4. 甲、乙两人参加某项活动,甲获奖的概率为0.5,乙获奖的概率为0.4,甲、乙两人同时获奖的概率为
0.2,则甲、乙两人恰有一人获奖的概率为( )
A. 0.3 B. 0.5 C. 0.7 D. 0.9
的
5. 如图,甲在 处观测到河对岸 某建筑物在北偏东 方向,顶部 的仰角为 ,往正东方向前进
第1页/共8页
学科网(北京)股份有限公司到达 处,测得该建筑物在北偏西 方向.底部 和 在同一水平面内,则该建筑物的高
为( )
A. B. C. D.
6. 已知 是三个不重合的平面, ,则( )
.
A 若 ,则
B. 若 ,则
C. 若 ,则
D. 若 ,则
7. 若 ,则 ( )
A. 1 B. C. D. 2
8. 向量 满足 ,则 的最大值为( )
A. B. C. D.
二、多选题:本题共3小,每小题6分,共18分.在每小题给出的四个选项中,有多个选项符
合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 某学校开展消防安全知识培训,对甲、乙两班学员进行消防安全知识测试,绘制测试成绩的频率分布直
方图,如图所示:( )
第2页/共8页
学科网(北京)股份有限公司的
A. 甲班成绩 平均数<甲班成绩的中位数
B. 乙班成绩的平均数 乙班成绩的中位数
C. 甲班成绩的平均数 乙班成绩的平均数
D. 乙班成绩的中位数 甲班成绩的中位数
10. 在梯形 中, ,则( )
A. B.
C. D. 在 上的投影向量为
11. 在长方体 中, ,动点 满足
,则( )
A. 当 时,
B. 当 时, 与 是异面直线
C. 当 时,三棱锥 的外接球体积的最大值为
D. 当 时,存在点 ,使得 平面
三、填空题:本题共3小题,每小题5分,共15分.
12. 向量 , ,若 ,则 ______.
第3页/共8页
学科网(北京)股份有限公司13. 在四棱锥 中, 底面 ,四边形 为正方形, ,则直线 与
所成角的大小为______.
14. 在 中, 为边 的中点, 的平分线交 于点 ,若 的面积为1,
则 的面积为______, 的最小值为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 某厂为了提升车载激光雷达质量的稳定性,对生产线进行升级改造、为了分析升级改造的效果,随机抽
取了12台车载激光雷达进行检测,检测结果如下:
序号 1 2 3 4 5 6 7 8 9 10 11 12
探测距离 (单位: ) 146 151 152 149 153 150 144 150 156
统计后得到样本平均数 ,方差 .
(1)升级改造后,若有 的产品的探测距离在 内,则认为升级改造成功;若改造成功且
有 的产品的探测距离在 内,则认为升级改造效果显著.根据样本数据,分析此次升级
改造的效果;
(2)采用在 内的数据作为新样本,求新样本的平均数 和方差 .
16. 甲每次投篮投进的概率是0.7,连续投篮三次,每次投篮结果互不影响,记事件A为“甲至少投进两球
(1)用 表示甲第 次的投篮结果,则 表示试验的样本点.用1表示“投进”,0表
示“未投进”,写出该试验的样本空间,判断其是否为古典概型,并说明理由;
(2)用计算机产生 之间的整数随机数,当出现随机数 时,表示“投进”,出现7,8,9时表
示“未投进”,以每3个随机数为一纽,代表甲三次投篮结果,产生20组随机数:
第4页/共8页
学科网(北京)股份有限公司的
利用该模拟试验,估计事件A 概率,并判断事件A的概率的精确值与估计值是否存在差异,并说明理由
17. 已知 分别为锐角三角形 三哥内角 的对边,且 .
(1)求 ;
(2)已知 ,点 为 的垂心,求 的周长的最大值.
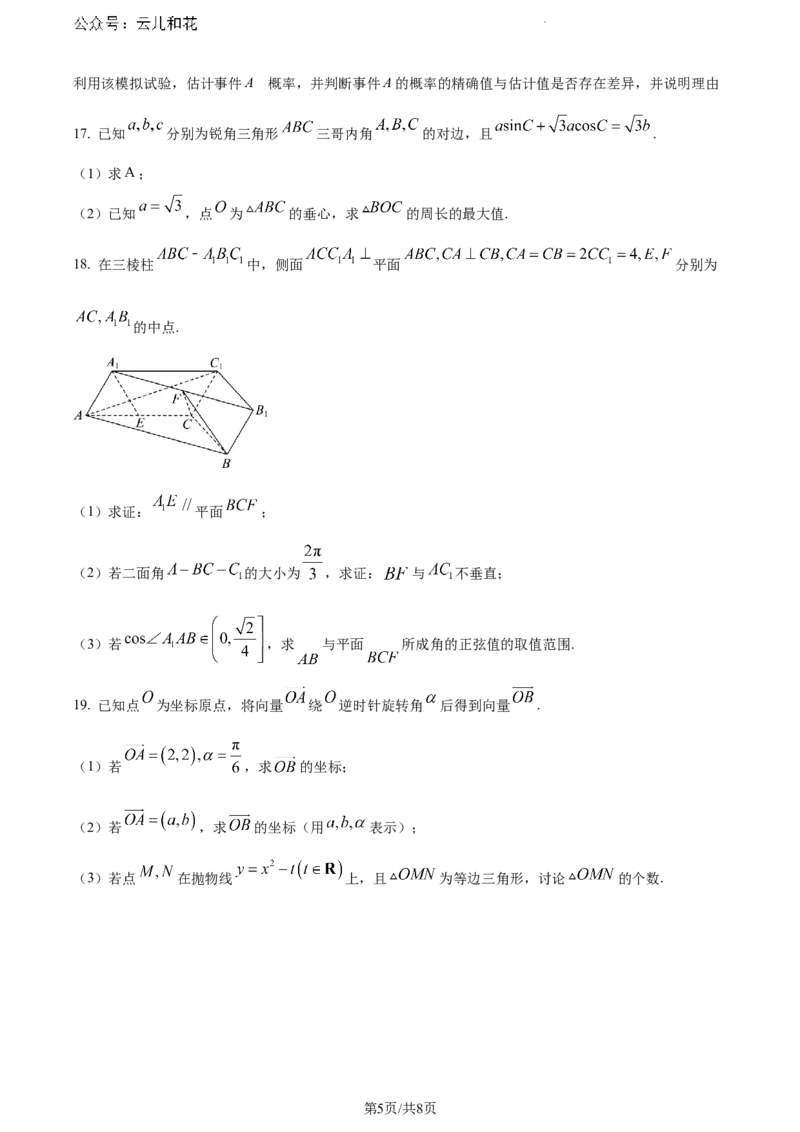
18. 在三棱柱 中,侧面 平面 分别为
的中点.
(1)求证: 平面 ;
(2)若二面角 的大小为 ,求证: 与 不垂直;
(3)若 ,求 与平面 所成角的正弦值的取值范围.
19. 已知点 为坐标原点,将向量 绕 逆时针旋转角 后得到向量 .
(1)若 ,求 的坐标;
(2)若 ,求 的坐标(用 表示);
(3)若点 在抛物线 上,且 为等边三角形,讨论 的个数.
第5页/共8页
学科网(北京)股份有限公司厦门市 2023—2024 学年第二学期高一期末质量检测
数学试题
满分:150分考试 时间:120分钟
考生注意:
1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的
条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将答题卡交回.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
【1题答案】
【答案】D
【2题答案】
【答案】C
【3题答案】
【答案】B
【4题答案】
【答案】B
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】A
【8题答案】
【答案】B
二、多选题:本题共3小,每小题6分,共18分.在每小题给出的四个选项中,有多个选项符
第6页/共8页
学科网(北京)股份有限公司合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】BC
【10题答案】
【答案】ACD
【11题答案】
【答案】ACD
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】
【答案】
【13题答案】
【答案】 ##
【14题答案】
【答案】 ①. 6 ②.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
【15题答案】
【答案】(1)答案见解析
(2)150,
【16题答案】
【答案】(1)样本空间见解析,不是古典概型,理由见解析
(2)事件A的概率的估计值为0.9,存在差异,理由见解析
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)证明见解析
第7页/共8页
学科网(北京)股份有限公司(2)证明见解析 (3)
【19题答案】
【答案】(1)
(2)
(3)答案见解析
第8页/共8页
学科网(北京)股份有限公司