文档内容
福建省泉州市泉州一中、泉港一中、德化一中、厦外石狮分校四校联盟
2025-2026学年高一上学期11月期中考试数学试题
一、单选题
1.化简 的结果是( )
A. B. C. D.
2.集合 , ,则 =( )
A. B. C. D.
3.已知幂函数 的图象与坐标轴没有公共点,则实数m的取值为 ( )
A. 或1 B. 或2 C.1 D.
4.下列命题为假命题的是( )
A.若 ,则 B.若 ,则
C.若 且 ,则 D.若 ,则
5.若“ ”是“ ”的必要不充分条件,则实数 的取值范围是( )
A. B. C. D.
6.函数 的图象大致为( )
A. B.C. D.
7.函数图象的渐近线是指曲线上一点M沿曲线无限远离原点时,M到某一条直线的距离无限趋近于零,
那么这条直线称为该曲线的渐近线,如函数 的两条渐近线分别是x轴与y轴.则直线y=3x是以下哪个
函数图象的一条渐近线( )
A. B. C. D.
8.定义在 上的奇函数 满足: ,且 , ,若 ,则不等
式 的解集为( )
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.当 时,幂函数 在 上单调递增
B.函数 的值域为
C.函数 的最小值是1
D.在同一坐标系中函数 与 的图象关于 轴对称
10.已知 ,且 ,则下列不等式恒成立的是( )
A. B.
C. D.11.分别用 , 表示 , 中的最小者和最大者,记为 ,
.若 , ,则( )
A.
B.函数 有2个零点
C.函数 的图象关于 轴对称
D.关于 的方程 的所有解的乘积为
三、填空题
12.已知 , ,则 .
13.若关于 的不等式 的解集为 ,则实数 的取值范围是 .
14.已知函数 , ,若方程 有且仅有 个不相等的解,则
的取值范围是 .
四、解答题
15.已知全集 ,集合 ,
(1)若 ,求
(2)若“ ”是“ ”充分不必要条件,求实数 a的取值范围.
16.已知函数 定义域为 .
(1)判断并证明 在 上的单调性;(2)求不等式 的解集.
17.如图,在平面直角坐标系中,有一个半径为2的半圆,直径 在x轴上, 中点为坐标原点O,等
腰梯形 的上底 的端点在圆周上.
(1)当 时,记梯形 位于直线 )左侧的图形的面积为 ,请写出函数 的解
析式.
(2)记线段 的长度为x,线段 与 的长度之和为y,求y的最大值.
18.已知 为偶函数, 为奇函数,且满足 .( )
(1)求 , 的解析式;
(2)令函数 ,求函数 的值域;
(3)存在 ,使得不等式 成立,求 的取值范围.
19.设函数 在区间 上有定义,若对任意 ,都存在 使得: ,则称函数
在区间 上具有性质 .
(1)判断函数 在 上是否具有性质 ,并说明理由;
(2)若函数 在区间 上具有性质 ,求实数 的取值范围;
(3)设 ,若存在唯一的实数 ,使得函数 在 上具有性质 ,求实数 的值.参考答案
1.B
【详解】因为 ,
所以 .
故选:B.
2.D
【详解】由题意可知 ,
∴ ,
故选:D
3.C
【详解】因为幂函数 的图象与坐标轴没有公共点,
所以 ,解得 .
故选:C.
4.A
【详解】对于A,取 ,由 ,可得 ,A错误,
对于B,因为 ,故 ,又 ,
所以 ,B正确,
对于C,因为 ,所以 ,
所以 ,又 ,
所以 ,C正确,
对于D,因为 ,
所以 ,
所以 ,D正确,
故选:A.5.C
【详解】根据题意,解不等式 ,即 ,
解得 ,即不等式的解集为 ,
若“ ”是“ ”的必要不充分条件,
则集合 是集合 的真子集,所以 .
故选:C
6.D
【详解】对于函数 ,定义域为 ,
因为 ,
所以函数 为偶函数,故B,C错误,
当 时, ,
又 在 上单调递增, 在 上单调递减,
故 在 上单调递增,故A错误,D正确.
故选:D.
7.B
【详解】 的渐近线也是x轴与y轴.故A错误.
对于选项B:当x很大时, 趋向于0.
故函数 的图象与直线 无限接近,故B正确.
类似的,C选项中的 的渐近线为直线 与y轴.
D选项当x很大时, 趋向于3,故它的渐近线为直线 与 .故选:B.
8.D
【详解】因为 ,且 , ,
所以 ,
设 ,
则 , ,且 ,,
根据单调性的定义可得, 在 上单调递增,
因为 在R上为奇函数,
所以 ,
所以 在R上为奇函数,
所以 在 上单调递增,
因为 ,
所以 ,则 ,
所以 的解集为 ,
所以 的解集为 .
故选:D
9.CD
【详解】对于A,当 时,函数定义域为 ,选项A错误;
对于B, ,函数 值域为 ,选项B错误;对于C, 函数 的最小值是1,故命题C正确;
对于D,在同一坐标系中,函数 与 的图象关于y轴对称,命题D正确.
故选:CD
10.BCD
【详解】因为 ,所以 ,
当且仅当 时,等号成立,故A错误;
因为 ,所以 ,
当且仅当 时,等号成立,故B正确
所以 ,当且仅当 时,等号成立,故C正确;
因为 ,所以 ,
所以 ,当且仅当 时,等号成立,故D正确.
故选:BCD
11.ACD
【详解】依题意, ,当 时, ;当 时, ,
则 , ,
对于A, ,A正确;
对于B, ,由 ,解得 ,B错误;
对于C, ,令 , ,函数 是偶函数,C正确;
对于D,由 ,得 或 ,
而 ,则 ,即 ,该方程有且仅有一个正根 ,
或 ,
,该方程有且仅有一个负根 ,且 ,
,该方程要么无解,要么一解 ,要么两个正根 ,
且 ,所以关于 的方程 的所有解的乘积为 ,D正确.
12.
【详解】因为 , ,
所以 ,
,
两式相加可得 ,所以 .
故答案为:
13.
【详解】设 ,
故由题意可得关于 的不等式 在区间 上恒成立,
.
故答案为:
14.
【详解】法一:当 时, ( 时等号成立),当 时, 在 单调递减且 , 的图象如图所示,
令 , ,即 ,
由 有 个不等解等价于 有两根,
其中一根 ,另一根 ,
根据韦达定理, , ,则 , ,
,由 ,所以 .
法二:可知由 有 个不等解等价于 有两根,其中一根 ,另一根 ,
所以 ,
由①得 ,则 ,
将④代入②得: ⑤
又由③得 ⑥,
由⑤⑥可知 ,所以 .
故答案为: .
15.(1)
(2)【详解】(1)当 时, , 或 ,
因为 ,所以 ;
(2)若“ ”是“ ”的充分不必要条件,即 ,
当 时, ,此时 ,满足 ,
当 时,则 ,解得: ,且 和 不能同时成立,
综上所述:实数a的取值范围为
16.(1)减函数,证明见解析
(2)
【详解】(1)函数 在 上为减函数.
证明如下:
任意 且 ,
则 ,
因为 ,所以 , ,
所以 ,即 ,所以函数 在 上为减函数.
(2)对任意的 , 且 ,所以 为奇函数,
由题意,不等式 可化为 ,
所以 ,解得 ,所以该不等式的解集为 .
17.(1)
(2) .
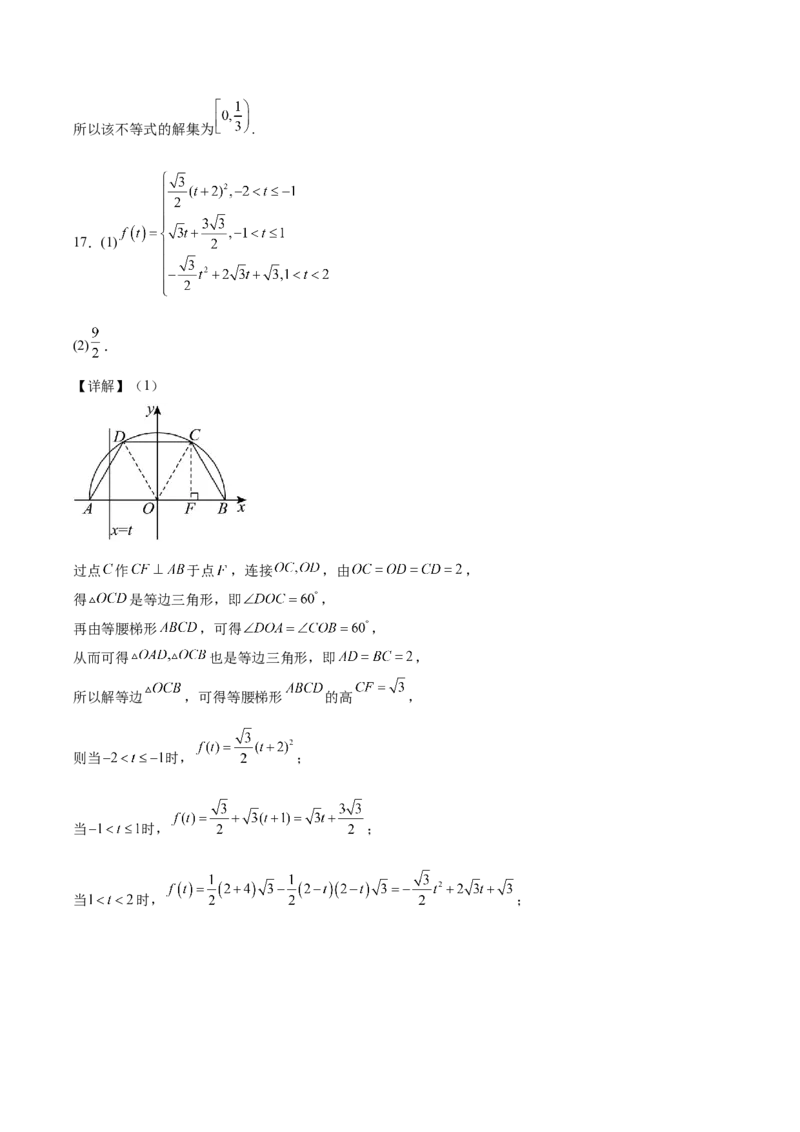
【详解】(1)
过点 作 于点 ,连接 ,由 ,
得 是等边三角形,即 ,
再由等腰梯形 ,可得 ,
从而可得 也是等边三角形,即 ,
所以解等边 ,可得等腰梯形 的高 ,
则当 时, ;
当 时, ;
当 时, ;所以 .
(2)连接OC,因为半圆的半径为2,线段 的长度为x,
则OC=2, , ,所以 ,
因此 ,
所以 ,其中 ,
令 ,因为 ,所以 ,
则 ,
所以 ,
当且仅当 ,即 时,取得最大值,
因此y的最大值为 .
18.(1) ,
(2)
(3)
【详解】(1)由 ,可得 ,
因为 为偶函数, 为奇函数,所以 ,联立方程组 ,
解得 , .
(2)由(1)
,∴ 为奇函数
当 时, , ,
因为 为奇函数,所以,当 时,
所以,函数 的值域为
(3)由(1)知 , ,
因为 ,所以 ,
可得 ,
所以 ,即 ,
设 ,
则 ,即 ,
当 时,则 ,不合题意;
当 时,则 ,设 ,则只需 ,
则 ,
当且仅当 ,即 时,等号成立,所以 ,解得 ,
综上可得,实数 的取值范围为 .
19.(1)指数函数 在 上不具有性质 ,理由见解析;
(2)
(3) 或
【详解】(1)指数函数 在 上不具有性质 .
理由如下:指数函数 的定义域为 ,
对于 ,易知 不存在 满足题意,
因此对于 ,不存在 满足 ,
即函数 在 上不具有性质 .
(2)因为函数 在区间 上具有性质 ,
所以对任意 ,都存在 使得 ,即 ,
可得 ,
因为 ,所以 ,又 ,所以 ,
即 ,解得 ,
因此实数 的取值范围为 .
(3)若函数 在 上具有性质 ,则对任意 ,都存在 使得 ,即 ;
因为 ,所以 ;
若 ,易知函数 关于 对称,
当 时,即 ,此时 在 上单调递减,此时 ;
因此可得 ,即 ,
解得 ,若存在唯一的实数 可得 ,
解得 ,符合题意;
当 时,可得 ,此时 在 的最小值为 ,
最大值为 ,即 ;
所以 ,即 ,
解得 ,若存在唯一的实数 可得 ,
解得 (舍)或 (舍);
当 时,可得 ,此时 在 的最小值为 ,
最大值为 ,即 ;
所以 ,即 ,
解得 ,若存在唯一的实数 可得 ,解得 或 (舍),即 符合题意;