文档内容
第八章 立体几何初步
(A 基础卷)
班级______ 姓名_______ 考号______
一、单项选择题(本大题共8题,每小题5分,共计40分。每小题列出的四个选项中只有一
项是最符合题目要求的)
1.设 , 是两条不同的直线, 是一个平面,则下列命题正确的是( )
A.若 , ,则 B.若 , ,则
C.若 , ,则 D.若 , ,则
2.如果一个长方体的长、宽、高分别是6,5,3,则它的体积为( )
A.15 B.18 C.30 D.90
3.一个圆柱的侧面展开图是一个边长为4的正方形,则这个圆柱的体积为( )
A. B. C. D.
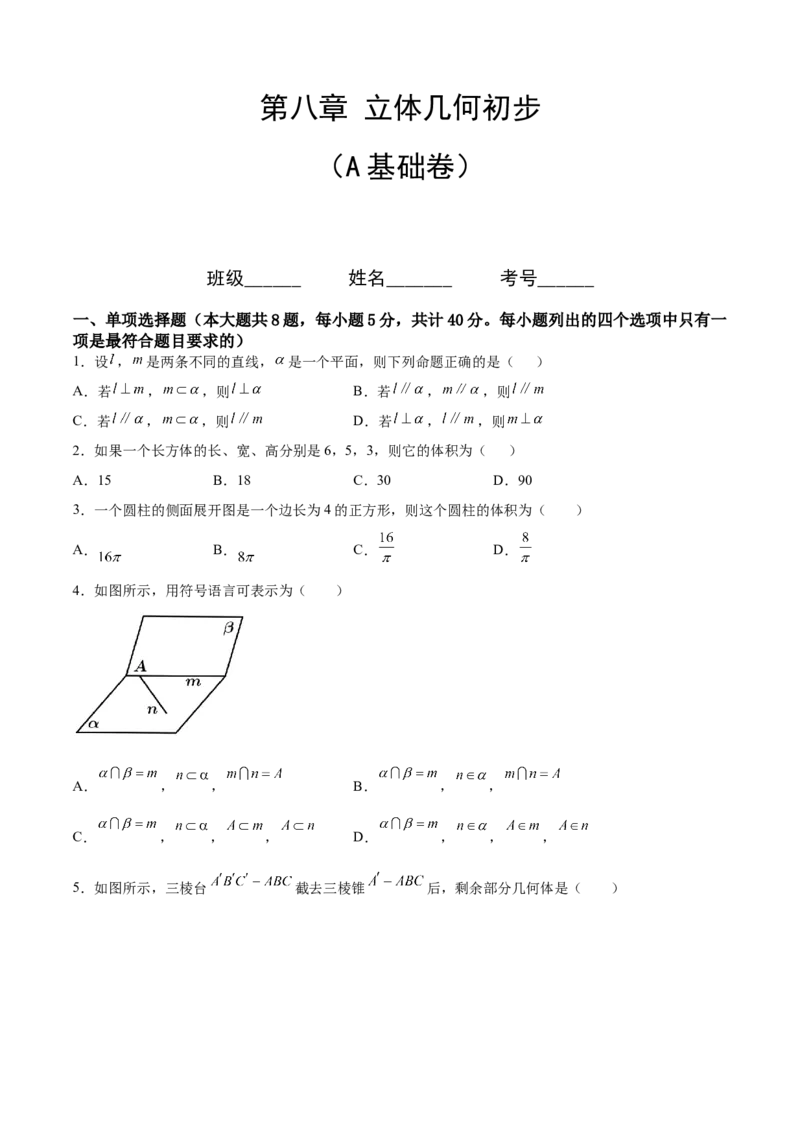
4.如图所示,用符号语言可表示为( )
A. , , B. , ,
C. , , , D. , , ,
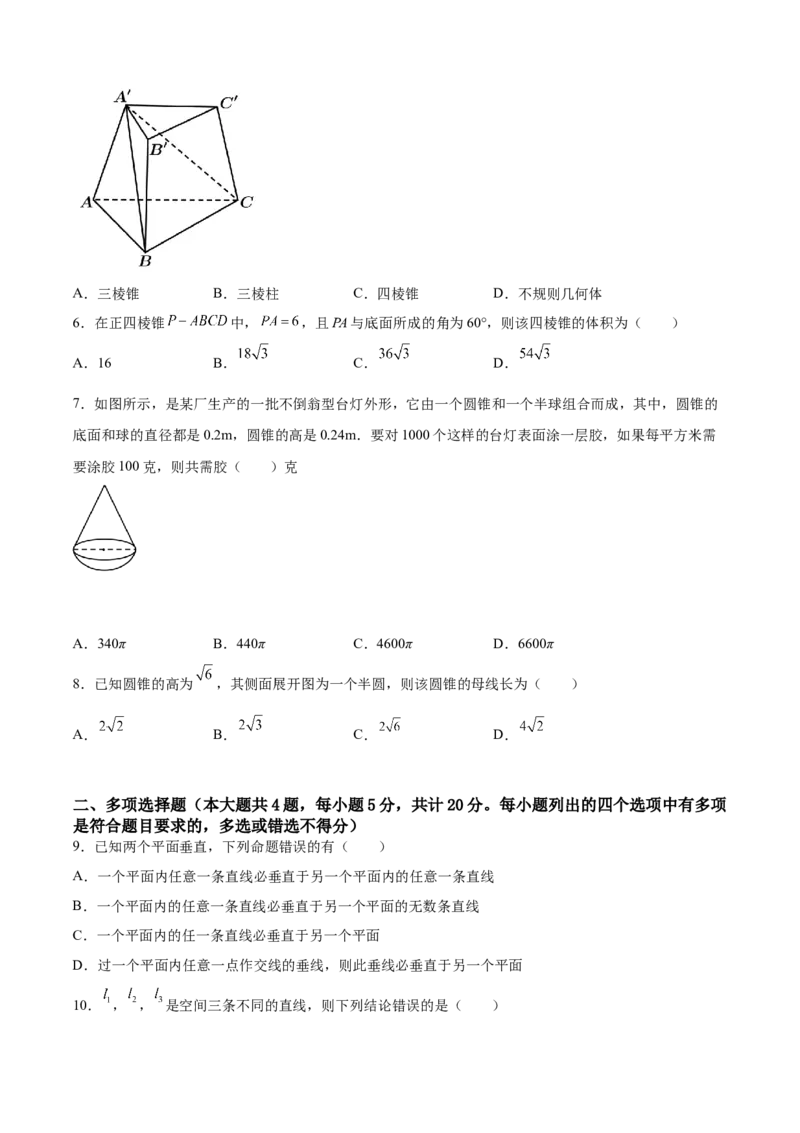
5.如图所示,三棱台 截去三棱锥 后,剩余部分几何体是( )A.三棱锥 B.三棱柱 C.四棱锥 D.不规则几何体
6.在正四棱锥 中, ,且PA与底面所成的角为60°,则该四棱锥的体积为( )
A.16 B. C. D.
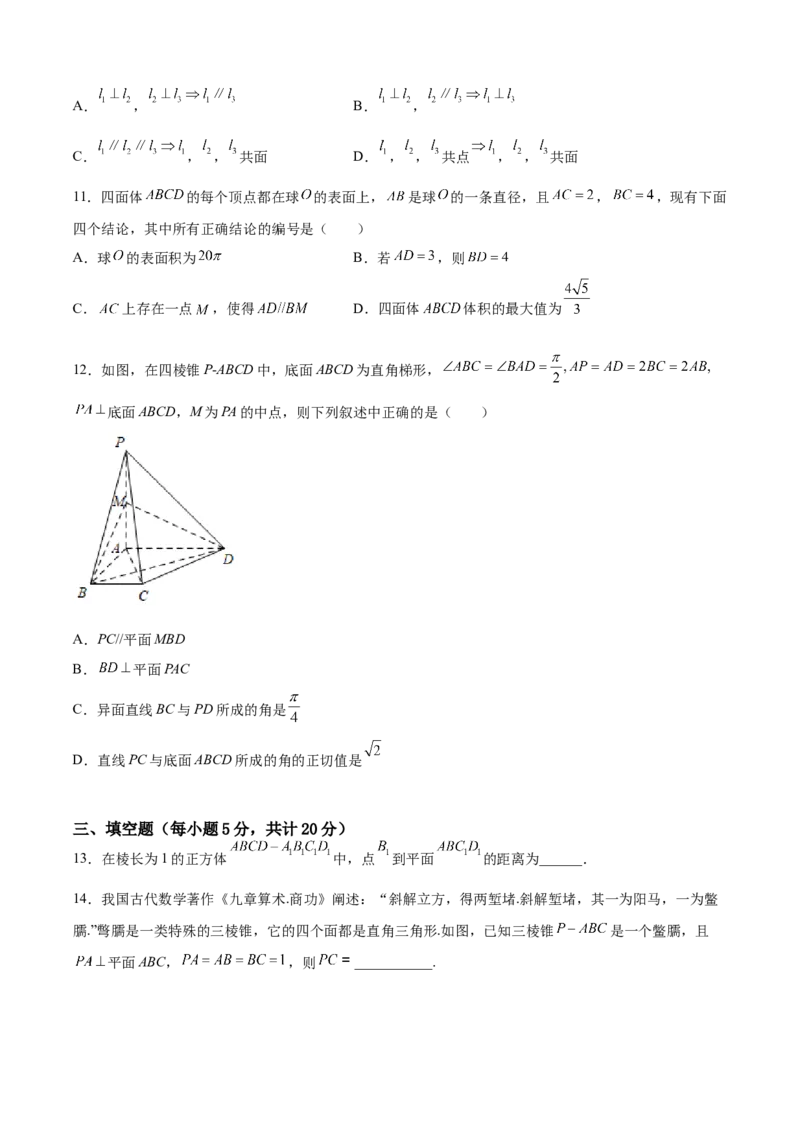
7.如图所示,是某厂生产的一批不倒翁型台灯外形,它由一个圆锥和一个半球组合而成,其中,圆锥的
底面和球的直径都是0.2m,圆锥的高是0.24m.要对1000个这样的台灯表面涂一层胶,如果每平方米需
要涂胶100克,则共需胶( )克
A.340π B.440π C.4600π D.6600π
8.已知圆锥的高为 ,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
二、多项选择题(本大题共4题,每小题5分,共计20分。每小题列出的四个选项中有多项
是符合题目要求的,多选或错选不得分)
9.已知两个平面垂直,下列命题错误的有( )
A.一个平面内任意一条直线必垂直于另一个平面内的任意一条直线
B.一个平面内的任意一条直线必垂直于另一个平面的无数条直线
C.一个平面内的任一条直线必垂直于另一个平面
D.过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面
10. , , 是空间三条不同的直线,则下列结论错误的是( )A. , B. ,
C. , , 共面 D. , , 共点 , , 共面
11.四面体 的每个顶点都在球 的表面上, 是球 的一条直径,且 , ,现有下面
四个结论,其中所有正确结论的编号是( )
A.球 的表面积为 B.若 ,则
C. 上存在一点 ,使得 D.四面体 体积的最大值为
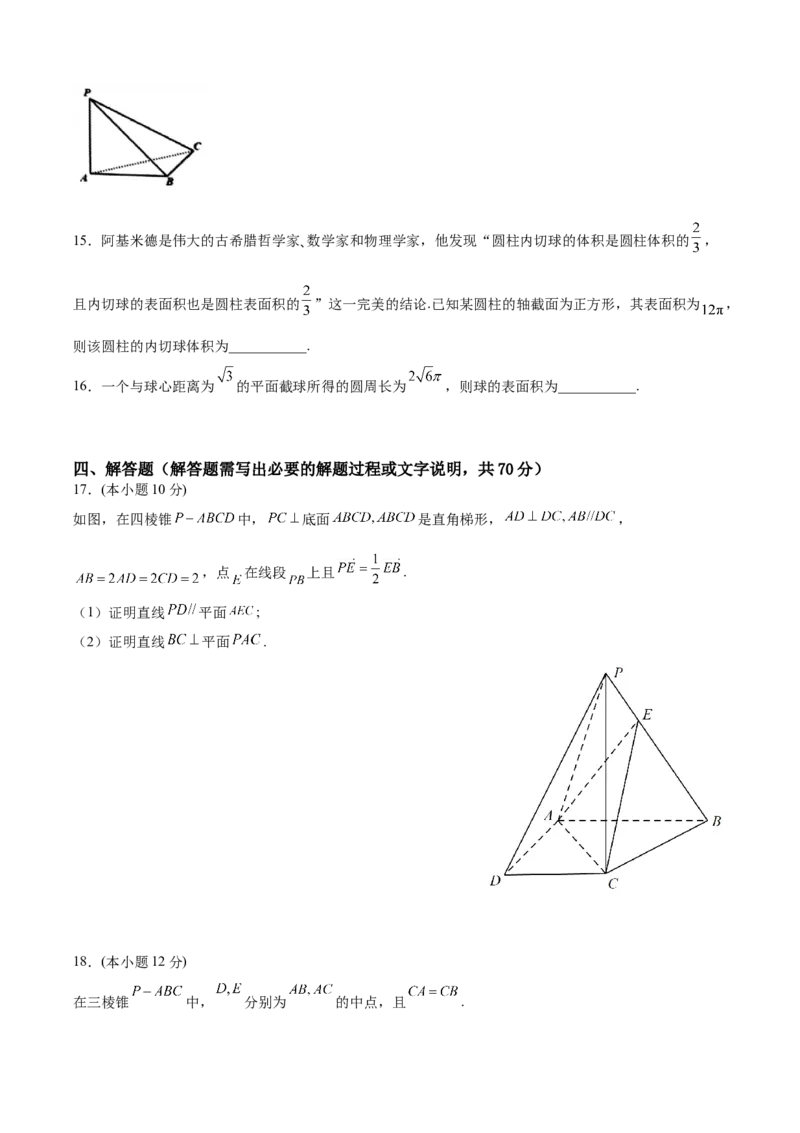
12.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,
底面ABCD,M为PA的中点,则下列叙述中正确的是( )
A.PC//平面MBD
B. 平面PAC
C.异面直线BC与PD所成的角是
D.直线PC与底面ABCD所成的角的正切值是
三、填空题(每小题5分,共计20分)
13.在棱长为1的正方体 中,点 到平面 的距离为______.
14.我国古代数学著作《九章算术.商功》阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖
臑.”彆臑是一类特殊的三棱锥,它的四个面都是直角三角形.如图,已知三棱锥 是一个鳖臑,且
平面ABC, ,则 ___________.15.阿基米德是伟大的古希腊哲学家、数学家和物理学家,他发现“圆柱内切球的体积是圆柱体积的 ,
且内切球的表面积也是圆柱表面积的 ”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为 ,
则该圆柱的内切球体积为___________.
16.一个与球心距离为 的平面截球所得的圆周长为 ,则球的表面积为___________.
四、解答题(解答题需写出必要的解题过程或文字说明,共70分)
17.(本小题10分)
如图,在四棱锥 中, 底面 是直角梯形, ,
,点 在线段 上且 .
(1)证明直线 平面 ;
(2)证明直线 平面 .
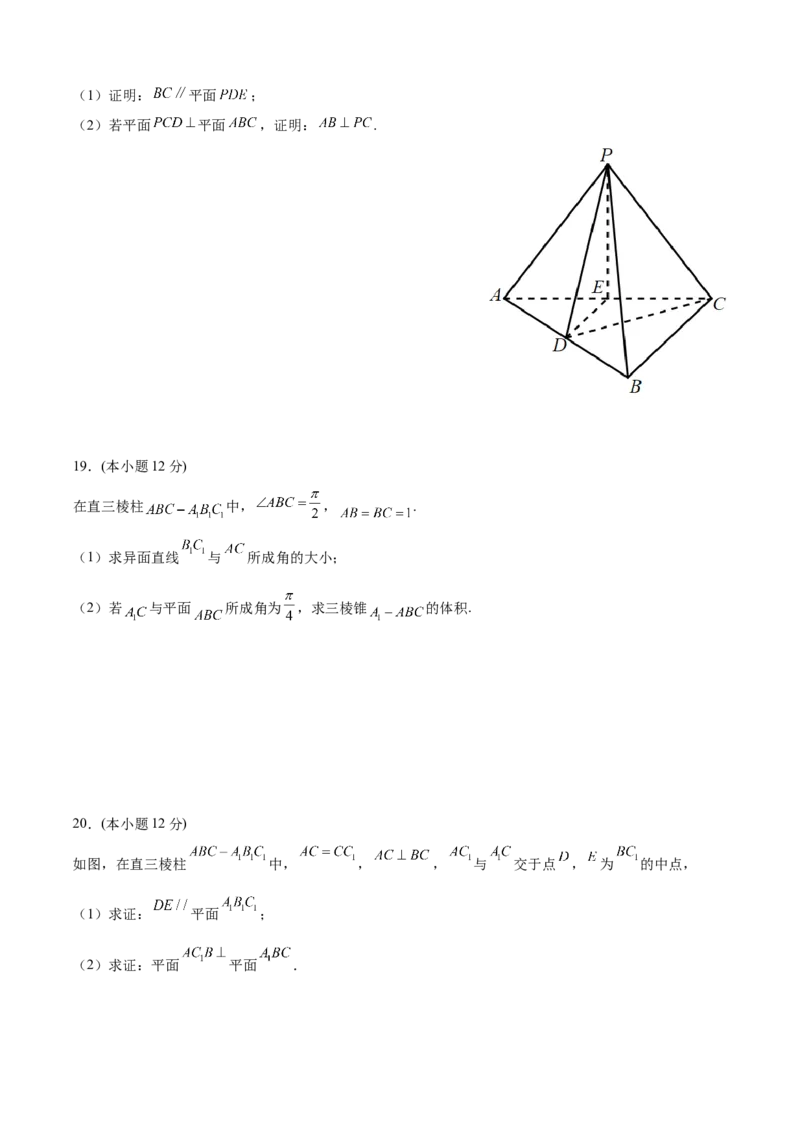
18.(本小题12分)
在三棱锥 中, 分别为 的中点,且 .(1)证明: 平面 ;
(2)若平面 平面 ,证明: .
19.(本小题12分)
在直三棱柱 中, , .
(1)求异面直线 与 所成角的大小;
(2)若 与平面 所成角为 ,求三棱锥 的体积.
20.(本小题12分)
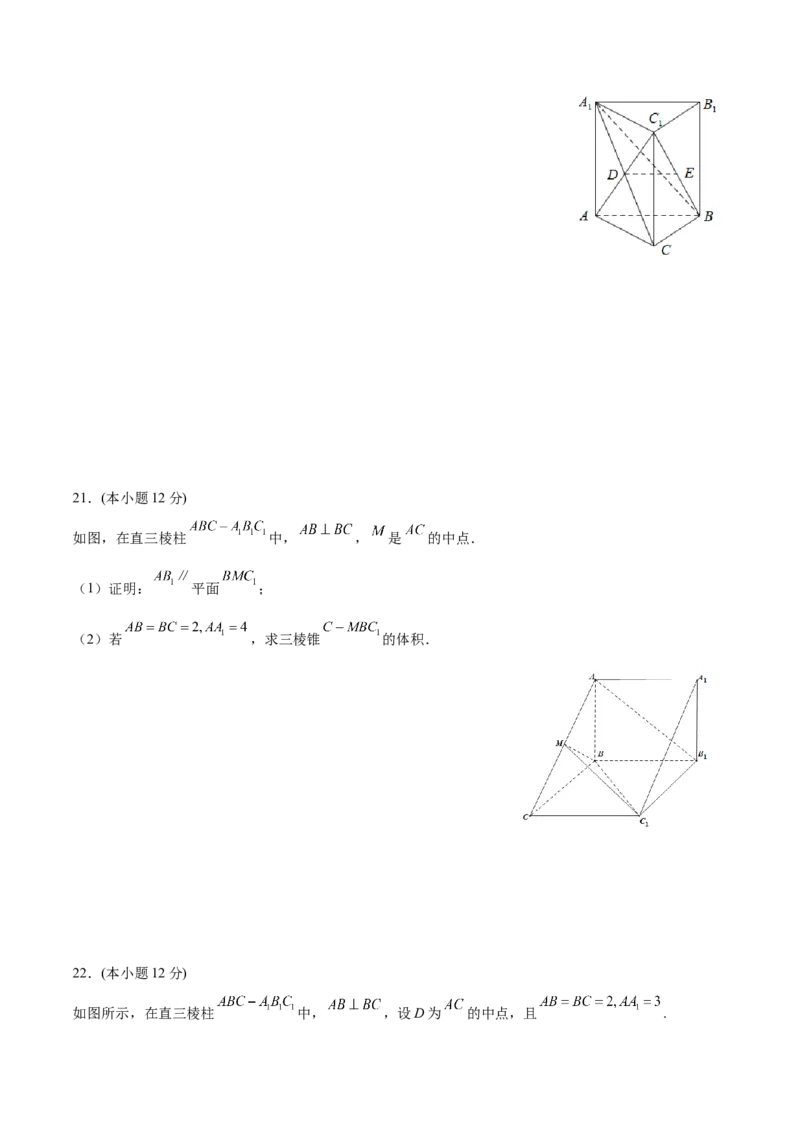
如图,在直三棱柱 中, , , 与 交于点 , 为 的中点,
(1)求证: 平面 ;
(2)求证:平面 平面 .21.(本小题12分)
如图,在直三棱柱 中, , 是 的中点.
(1)证明: 平面 ;
(2)若 ,求三棱锥 的体积.
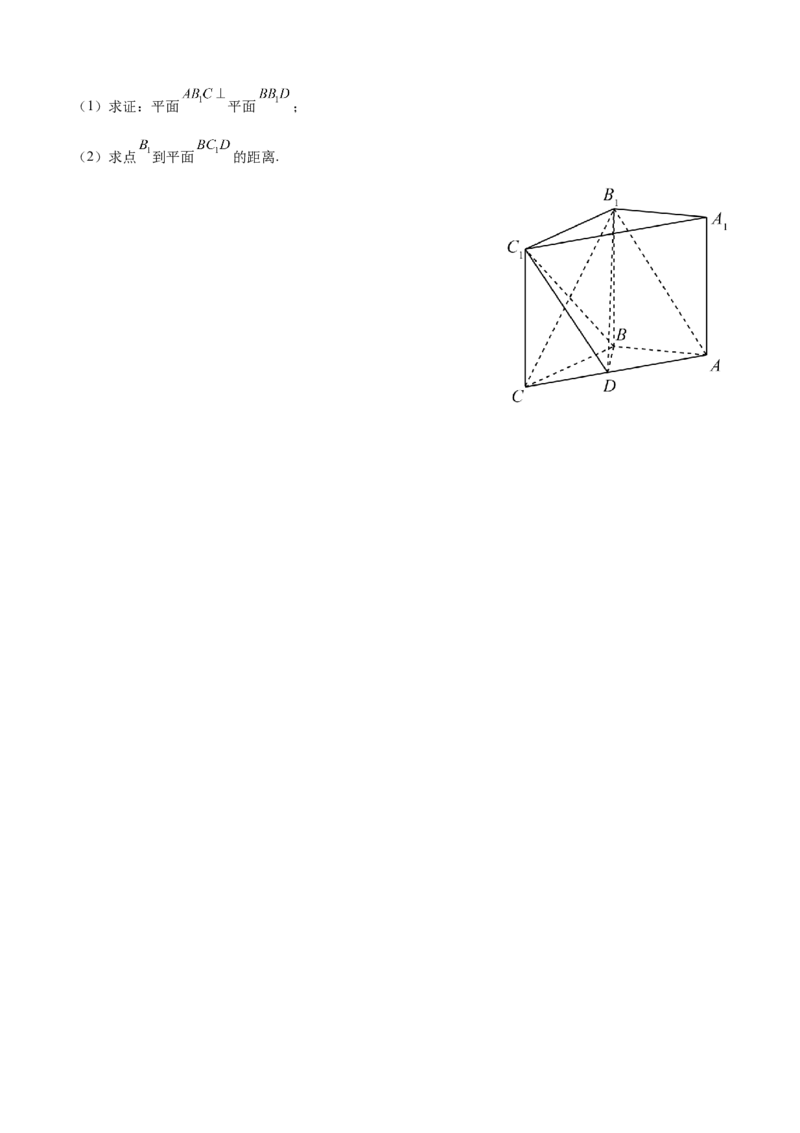
22.(本小题12分)
如图所示,在直三棱柱 中, ,设D为 的中点,且 .(1)求证:平面 平面 ;
(2)求点 到平面 的距离.