文档内容
第八章 章末测试
一、单选题(每题只有一个选项为正确答案,每题5分,8题共40分)
1.(2021·应城市第一高级中学高二期末)已知x与y之间的一组数据如下表:
x 3 4 5 6
y 30 40 60 50
若y与x线性相关,根据上表求得y与x的线性回归方程, 中的 为8,据此模型预报 时
y的值为( )
A.70 B.63 C.65 D.66
2.(2021·黄石市有色第一中学高二期末)下列关于回归分析的说法中错误的是( )
A.回归直线一定过样本中心
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.甲、乙两个模型的 分别约为 和 ,则模型乙的拟合效果更好
D.两个模型中残差平方和越小的模型拟合的效果越好
3.(2021·云南高二期末)某同学为了解气温对热饮销售的影响,经过统计分析,得到了一个卖出的热
饮杯数 与当天气温 的回归方程 .下列选项正确的是( )
A. 与 线性正相关 B. 与 线性负相关
C. 随 增大而增大 D. 随 减小而减小
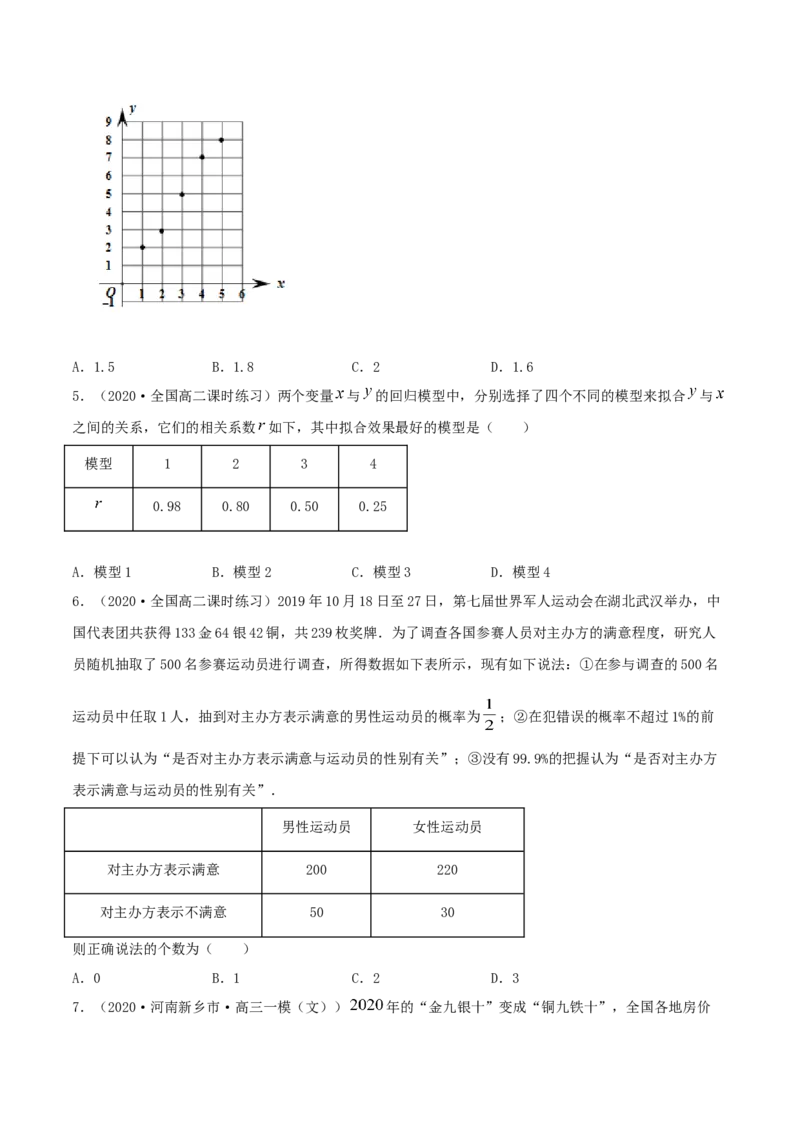
4.(2021·安徽阜阳市)如图,根据已知的散点图,得到y关于x的线性回归方程为 ,则
( )A.1.5 B.1.8 C.2 D.1.6
5.(2020·全国高二课时练习)两个变量 与 的回归模型中,分别选择了四个不同的模型来拟合 与
之间的关系,它们的相关系数 如下,其中拟合效果最好的模型是( )
模型 1 2 3 4
0.98 0.80 0.50 0.25
A.模型1 B.模型2 C.模型3 D.模型4
6.(2020·全国高二课时练习)2019年10月18日至27日,第七届世界军人运动会在湖北武汉举办,中
国代表团共获得133金64银42铜,共239枚奖牌.为了调查各国参赛人员对主办方的满意程度,研究人
员随机抽取了500名参赛运动员进行调查,所得数据如下表所示,现有如下说法:①在参与调查的500名
运动员中任取1人,抽到对主办方表示满意的男性运动员的概率为 ;②在犯错误的概率不超过1%的前
提下可以认为“是否对主办方表示满意与运动员的性别有关”;③没有99.9%的把握认为“是否对主办方
表示满意与运动员的性别有关”.
男性运动员 女性运动员
对主办方表示满意 200 220
对主办方表示不满意 50 30
则正确说法的个数为( )
A.0 B.1 C.2 D.3
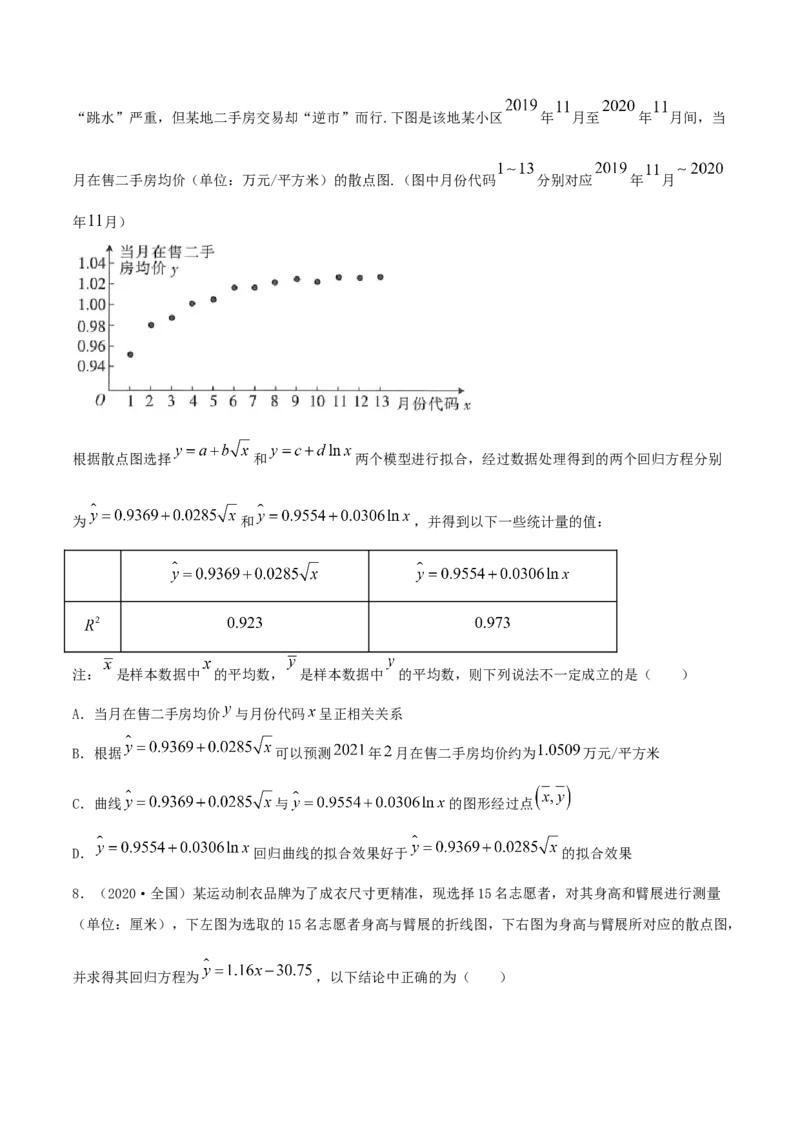
7.(2020·河南新乡市·高三一模(文)) 年的“金九银十”变成“铜九铁十”,全国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.下图是该地某小区 年 月至 年 月间,当
月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码 分别对应 年 月
年 月)
根据散点图选择 和 两个模型进行拟合,经过数据处理得到的两个回归方程分别
为 和 ,并得到以下一些统计量的值:
注: 是样本数据中 的平均数, 是样本数据中 的平均数,则下列说法不一定成立的是( )
A.当月在售二手房均价 与月份代码 呈正相关关系
B.根据 可以预测 年 月在售二手房均价约为 万元/平方米
C.曲线 与 的图形经过点
D. 回归曲线的拟合效果好于 的拟合效果
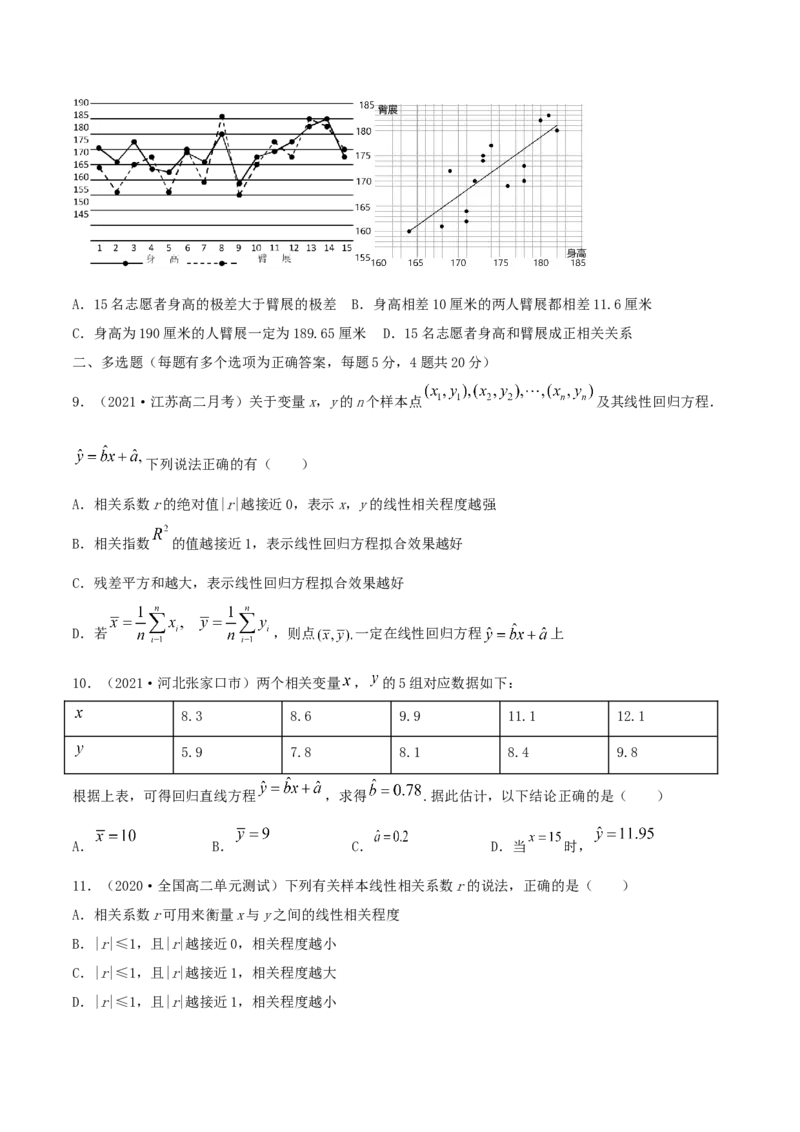
8.(2020·全国)某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量
(单位:厘米),下左图为选取的15名志愿者身高与臂展的折线图,下右图为身高与臂展所对应的散点图,
并求得其回归方程为 ,以下结论中正确的为( )A.15名志愿者身高的极差大于臂展的极差 B.身高相差10厘米的两人臂展都相差11.6厘米
C.身高为190厘米的人臂展一定为189.65厘米 D.15名志愿者身高和臂展成正相关关系
二、多选题(每题有多个选项为正确答案,每题5分,4题共20分)
9.(2021·江苏高二月考)关于变量x,y的n个样本点 及其线性回归方程.
下列说法正确的有( )
A.相关系数r的绝对值|r|越接近0,表示x,y的线性相关程度越强
B.相关指数 的值越接近1,表示线性回归方程拟合效果越好
C.残差平方和越大,表示线性回归方程拟合效果越好
D.若 ,则点 一定在线性回归方程 上
10.(2021·河北张家口市)两个相关变量 , 的5组对应数据如下:
8.3 8.6 9.9 11.1 12.1
5.9 7.8 8.1 8.4 9.8
根据上表,可得回归直线方程 ,求得 .据此估计,以下结论正确的是( )
A. B. C. D.当 时,
11.(2020·全国高二单元测试)下列有关样本线性相关系数r的说法,正确的是( )
A.相关系数r可用来衡量x与y之间的线性相关程度
B.|r|≤1,且|r|越接近0,相关程度越小
C.|r|≤1,且|r|越接近1,相关程度越大
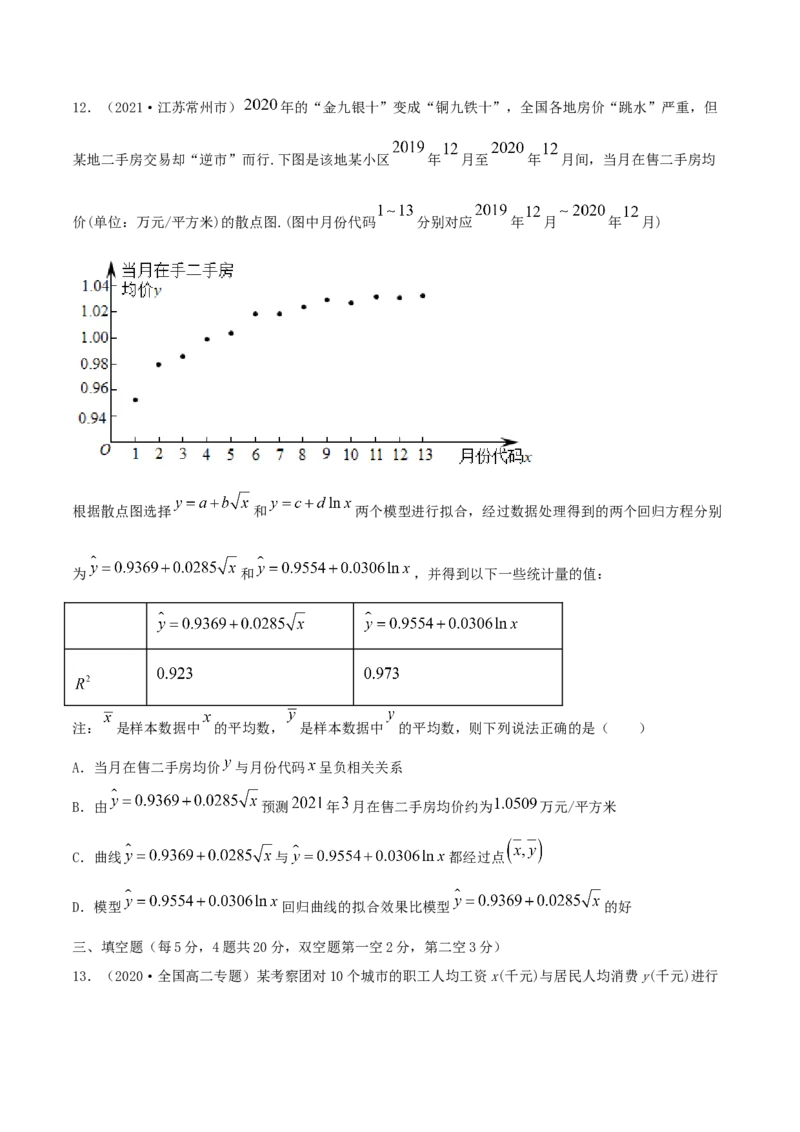
D.|r|≤1,且|r|越接近1,相关程度越小12.(2021·江苏常州市) 年的“金九银十”变成“铜九铁十”,全国各地房价“跳水”严重,但
某地二手房交易却“逆市”而行.下图是该地某小区 年 月至 年 月间,当月在售二手房均
价(单位:万元/平方米)的散点图.(图中月份代码 分别对应 年 月 年 月)
根据散点图选择 和 两个模型进行拟合,经过数据处理得到的两个回归方程分别
为 和 ,并得到以下一些统计量的值:
注: 是样本数据中 的平均数, 是样本数据中 的平均数,则下列说法正确的是( )
A.当月在售二手房均价 与月份代码 呈负相关关系
B.由 预测 年 月在售二手房均价约为 万元/平方米
C.曲线 与 都经过点
D.模型 回归曲线的拟合效果比模型 的好
三、填空题(每5分,4题共20分,双空题第一空2分,第二空3分)
13.(2020·全国高二专题)某考察团对10个城市的职工人均工资x(千元)与居民人均消费y(千元)进行调查统计,得出y与x具有线性相关关系,且回归方程为 .若某城市职工人均工资为5千元,
估计该城市人均消费额占人均工资收入的百分比为________.
14.(2020·全国)在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是________.
(填序号)
①若 的观测值为 ,在犯错误的概率不超过 的前提下认为吸烟与患肺癌有关系,那么在
个吸烟的人中必有 人患有肺癌;
②由独立性检验可知,在犯错误的概率不超过 的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,
那么他有 的可能患有肺癌;
③若从统计量中求出在犯错误的概率不超过 的前提下认为吸烟与患肺癌有关系,是指有 的可能性
使得判断出现错误
15.(2020·全国)2020年4月份,华为举行中国区春季新品发布会,华为消费者业务 余承东正式
发布 系列 手机.现调查得到该系列手机上市时间 和市场占有率 (单位: 的几组相关对应
数据,绘制如图所示的折线图,图中的 ,2,3,4,5, ,分别代表2020年的4月份,5月份,6月
份,7月份,8月份, .据此数据得出 关于 的回归方程为 ,用此方程预测该系列手
机市场占有率的变化趋势,要使该系列手机的市场占有率超过 ,最早应在2021年的__月份.
16.(2020·西安市长安区第五中学)面对竞争日益激烈的消费市场,众多商家不断扩大自己的销售市场,以降低生产成本.某白酒酿造企业市场部对该企业9月份的产品销量(千箱)与单位成本(元)的资料进行
线性回归分析,结果如下: , , , ,
, ,则销量每增加1千箱,单位成本下降
________元 .
四、解答题(17题10分,其余每题12分,共70分)
17.(2021·河南)为激活国内消费市场,挽回疫情造成的损失,国家出台一系列的促进国内消费的优惠
政策,某机构从某一电商的线上交易大数据中来跟踪调查消费者的购买力,界定3至8月份购买商品在
5000元以上人群属“购买力强人群”,购买商品在5000元以下人群属“购买力弱人群”.现从电商平台
消费人群中随机选出200人,发现这200人中属购买力强的人数占80%,并将这200人按年龄分组,记第1
组 ,第2组 ,第3组 ,第4组 ,第5组 ,得到频率分布直方图,
如图.
(1)求出频率分布直方图中的 值和这200人的平均年龄;
(2)从第1,2组中用分层抽样的方法抽取5人,并再从这5人中随机抽取2人进行电话回访,求这两人
恰好属于不同组别的概率;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中“购买力弱人群”的中老年人有20人,问是否有99%的把握认为是否属“购买力强人群”与年龄有关?
附:
0.150 0.100 0.050 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
,
18.(2021·广东清远市·高二期末)某企业投资两个新型项目,投资新型项目 的投资额 (单位:十
万元)与纯利润 (单位:万元)的关系式为 ,投资新型项目 的投资额 (单位:十万
元)与纯利润 (单位:万元)的散点图如图所示.
(1)求 关于 的线性回归方程;(2)根据(1)中的回归方程,若 , 两个项目都投资60万元,试预测哪个项目的收益更好.
附:回归直线 的斜率和截距的最小二乘估计分别为 , .
19.(2021·河南驻马店市)近年来,共享单车进驻城市,绿色出行引领时尚.某公司计划对未开通共享
单车的 县城进行车辆投放,为了确定车辆投放量,对过去在其他县城的投放量情况以及年使用人次进行
了统计,得到了投放量 (单位:千辆)与年使用人次 (单位:千次)的数据如下表所示,根据数据绘
制投放量 与年使用人次 的散点图如图所示.
(1)观察散点图,可知两个变量不具有线性相关关系,拟用对数函数模型 或指数函数模型对两个变量的关系进行拟合,请问哪个模型更适宜作为投放量 与年使用人次 的
回归方程类型(给出判断即可,不必说明理由),并求出 关于 的回归方程;
(2)已知每辆单车的购入成本为 元,年调度费以及维修等的使用成本为每人次 元,按用户每使用
一次,收费 元计算,若投入 辆单车,则几年后可实现盈利?
参考数据:
其中 , .
参考公式:对于一组数据 , ,…, ,其回归直线 的斜率和截距的最小
二乘估计公式分别为 , .
20.(2021·江苏泰州市)2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱
贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在
产业扶贫政策的大力支持下,西部某县新建了甲、乙两家玩具加工厂,加工同一型号的玩具质监部门随机
抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A”、“B”、“C”三
个等级,A、B等级都是合格品,C等级是次品,统计结果如下表所示:
等级 A B C
频数 20 120 60
(表一)
厂家 合格品 次品 合计
甲 75乙 35
合计
(表二)
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销.
(1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率
与厂家有关?
(2)每件玩具的生产成本为30元,A、B等级产品的出厂单价分别为60元、40元.另外已知每件次品的销毁
费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲、乙两厂能否都能盈
利,并说明理由.
附: ,其中 .
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
21.(2020·长沙市·湖南师大附中高二期中)近年来,我国肥胖人群的规模急速增长,肥胖人群有很大
的心血管安全隐患.目前,国际上常用身体质量指数(BodyMassIndex,缩写 )来衡量人体胖瘦程度
以及是否健康,其计算公式是 .中国成人的 数值标准为: 为
偏瘦; 为正常; 为偏胖; 为肥胖.为了解某公司员工的身
体质量指数,研究人员从公司员工体检数据中,抽取了8名员工(编号1~8)的身高 和体重
数据,并计算得到他们的 值(精确到0.1)如表:
编号 1 2 3 4 5 6 7 8
身高 164 176 165 168 182体重 60 72 77 72 55
(近似
22.3 23.2 28.3 20.3 23.5 23.7 25.5 16.6
值)
(1)现从这8名员工中选取2人进行复检,求至少一人 值“正常”的概率.
(2)某调查机构分析发现公司员工的身高 和体重 之间有较强的线性相关关系,在部分体检
数据丢失之前调查员甲已进行相关的数据分析,并计算得出该组数据的线性回归方程为 ,且根
据回归方程预估一名身高为 的员工体重为 .计算得到的其他数据如下: ,
.
①求 的值及表格中体重的平均值 ;
②在数据处理时,调查员乙发现编号为8的员工体重数据有误,应为增加 为 ,身高数据无误.请
你根据调查员乙更正的数据重新计算线性回归方程,并据此预估一名身高为 的员工的体重.
(附:对于一组数据 , ,…, ,其回归直线 的斜率和截距的最小二乘
法估计分别为: , .
22.(2021·湖南长沙市·长沙一中)定向越野起源于欧洲,是一种借助地图、指南针,在一个划定的区
域内,通过对地形地貌的判断.设计合理路线到达各个目标点位,最后到达终点的运动.湖南青奠定向体育
发展有限公司为了推广定向活动,对学生群体进行定向越野的介绍和培训,并对初步了解了定向活动的学
生是否会参加定向越野活动进行调查.随机抽取了200位中小学生进行调查,得到如下数据:准备参加定向
越野的小学生有80人,不准备参加定向越野的小学生有40人,准备参加定向越野的中学生有40人.(1)完成下列 列联表,并根据列联表判断是否有97.5%的把握认为这200位参与调查的中小学生是否
准备参加定向越野与中学生、小学生年龄有关.
准备参加定向越野 不准备参加定向越野 合计
小学生
中学生
合计
(2)为了储备定向后备力量,备战全国赛,提高会员定向水平,俱乐部将小学生会员分组进行比赛.两人
一组,每周进行一轮比赛,每小组两人每人跑两张地图(跑一张地图视为一次),达到教练设定的成绩标准
的次数之和不少于3次称为“优秀小组”.小超与小红同一小组,小超、小红达到教练设定的成绩标准的概
率分别为 , ,且 ,理论上至少要进行多少轮比赛,才能使得小超、小红小组在比赛中获
得“优秀小组”次数的期望值达到16次?并求此时 , 的值.
附: , .
0.50 0.25 0.05 0.025 0.010
0.455 1.323 3.840 5.024 6.635