文档内容
A级:“四基”巩固训练
一、选择题
1.给出下列函数:
①y=2·3x;②y=3x+1;③y=3x;④y=x3;⑤y=(-2)x.
其中,指数函数的个数是( )
A.0 B.1 C.2 D.3
答案 B
解析 形如y=ax(a>0,且a≠1)的函数叫指数函数,由定义知只有 y=3x是
指数函数.故选B.
2.已知函数f(x)=则f[f(-1)]=( )
A.2 B. C.0 D.
答案 B
解析 f(-1)=2-1=,f[f(-1)]=f=3=.
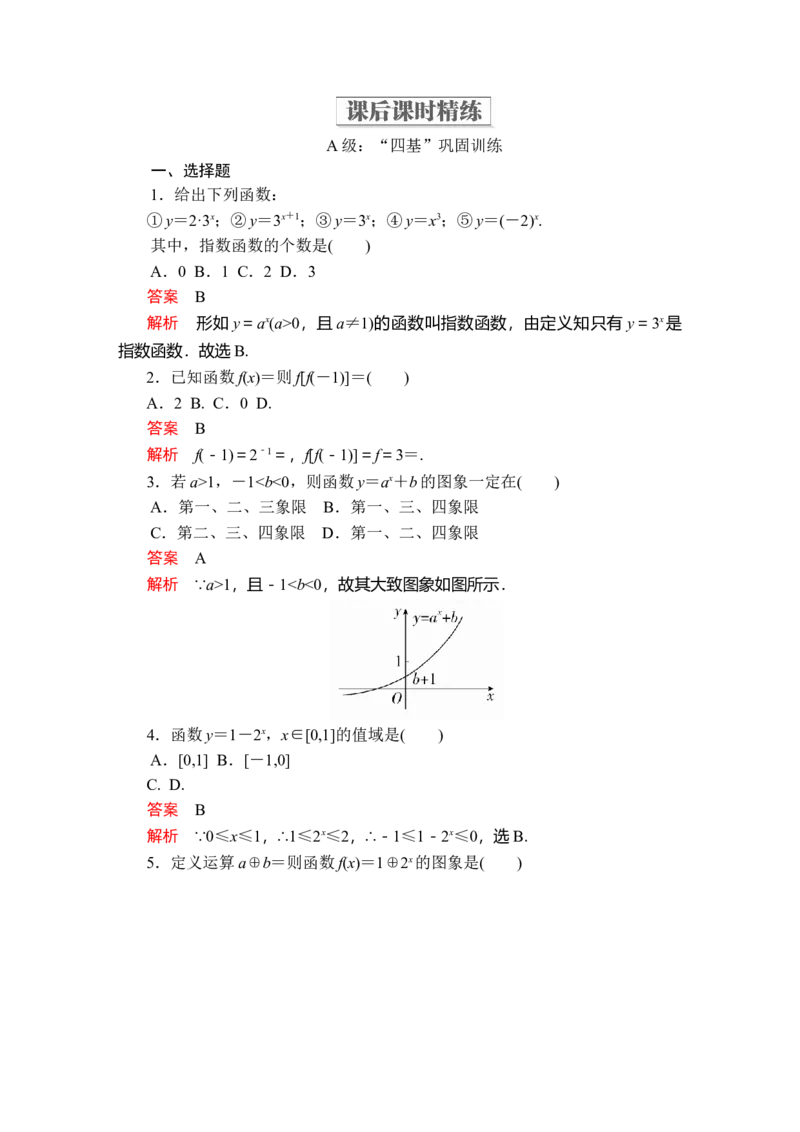
3.若a>1,-11,且-10时
f(x)=2x>1,所以a>0不成立,故a<0,即f(a)=a+1=-2,所以a=-3.
7.函数y=-2-x的图象一定过第________象限.
答案 三、四
解析 y=-2-x=-x与y=x关于x轴对称,一定过第三、四象限.
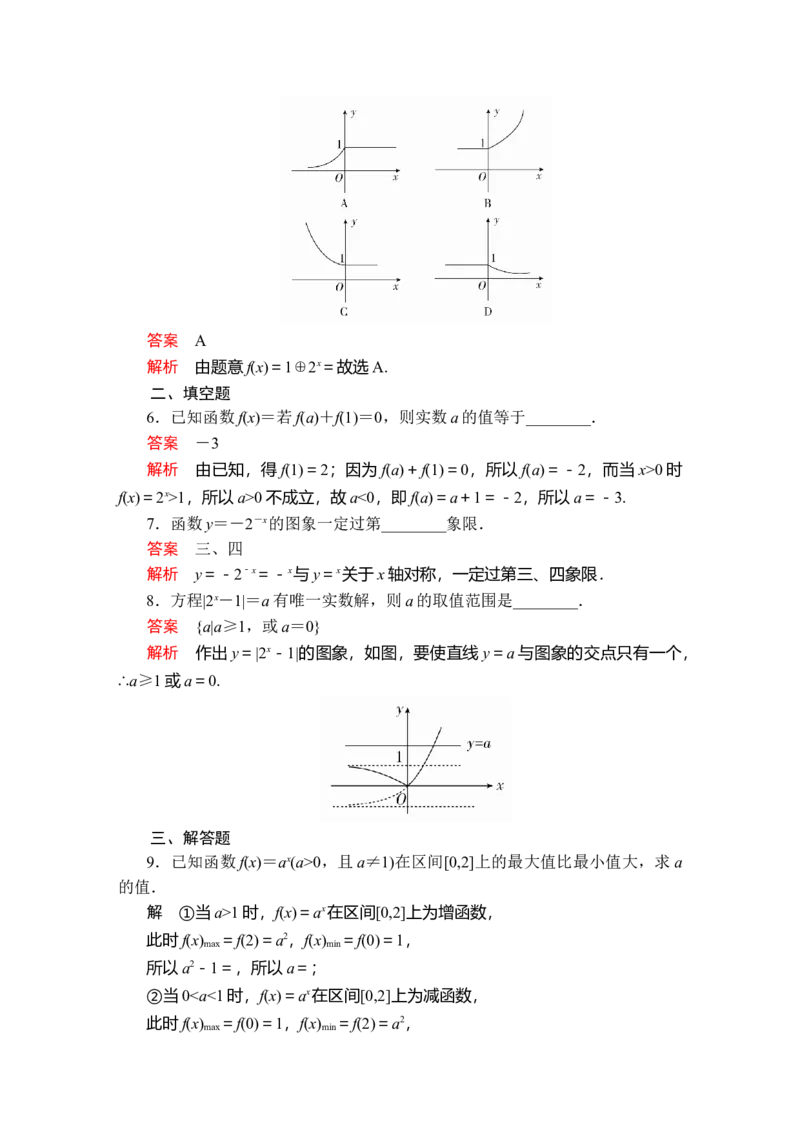
8.方程|2x-1|=a有唯一实数解,则a的取值范围是________.
答案 {a|a≥1,或a=0}
解析 作出y=|2x-1|的图象,如图,要使直线y=a与图象的交点只有一个,
∴a≥1或a=0.
三、解答题
9.已知函数f(x)=ax(a>0,且a≠1)在区间[0,2]上的最大值比最小值大,求a
的值.
解 ①当a>1时,f(x)=ax在区间[0,2]上为增函数,
此时f(x) =f(2)=a2,f(x) =f(0)=1,
max min
所以a2-1=,所以a=;
②当00,
1 2
故f(x )>f(x )>0,
1 2
所以(2,+∞)是f(x)的单调增区间,(-∞,2)是f(x)的单调减区间.
B级:“四能”提升训练
1.已知函数f(x)=.
(1)证明:函数f(x)是R上的增函数;
(2)求函数f(x)的值域;
(3)令g(x)=,判断函数g(x)的奇偶性,并简要说明理由.
解 (1)证明:设x ,x 是R上任意两个实数,且x >x ,
1 2 2 1
(2)f(x)==1-,
∵2x+1>1,∴0<<2,即-2<-<0,
∴-1<1-<1.
∴f(x)的值域为(-1,1).
(3)g(x)为偶函数.
由题意知g(x)==·x,
易知函数g(x)的定义域为(-∞,0)∪(0,+∞),
g(-x)=(-x)·=(-x)·=x·=g(x),∴函数g(x)为偶函数.
2.设x,y,z为正数,且2x=3y=5z.证明:5z>2x>3y.
证明 ∵2x=3y,∴22x=32y=(3)3y,
∴(23)2x=(32)3y.
∵32>23,3y>0,∴(32)3y>(23)3y,
故(23)2x>(23)3y.
由指数函数的单调性得2x>3y.
∵2x=5z,∴22x=52z=(5)5z,
∴(25)2x=(52)5z.
∵25>52,5z>0,∴(52)5z<(25)5z,
故(25)2x<(25)5z.
由指数函数的单调性得2x<5z.
综上,5z>2x>3y.