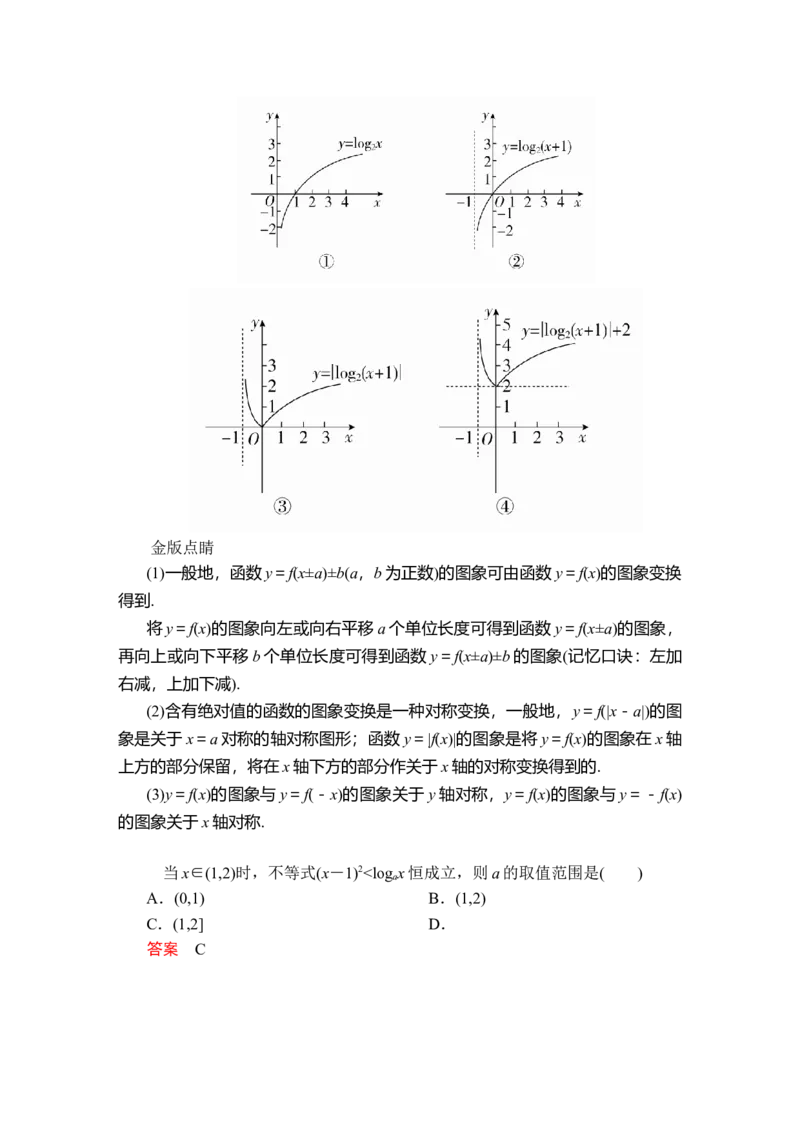
文档内容
4.4.2 对数函数的图象和性质
第 1 课时 对数函数的图象和性质
(教师独具内容)
课程标准:能用描点法或借助计算工具画出具体对数函数的图象,探索并了
解对数函数的单调性与特殊点.
教学重点:对数函数的图象及性质.
教学难点:底数a对图象的影响及对数函数性质的应用.
【知识导学】
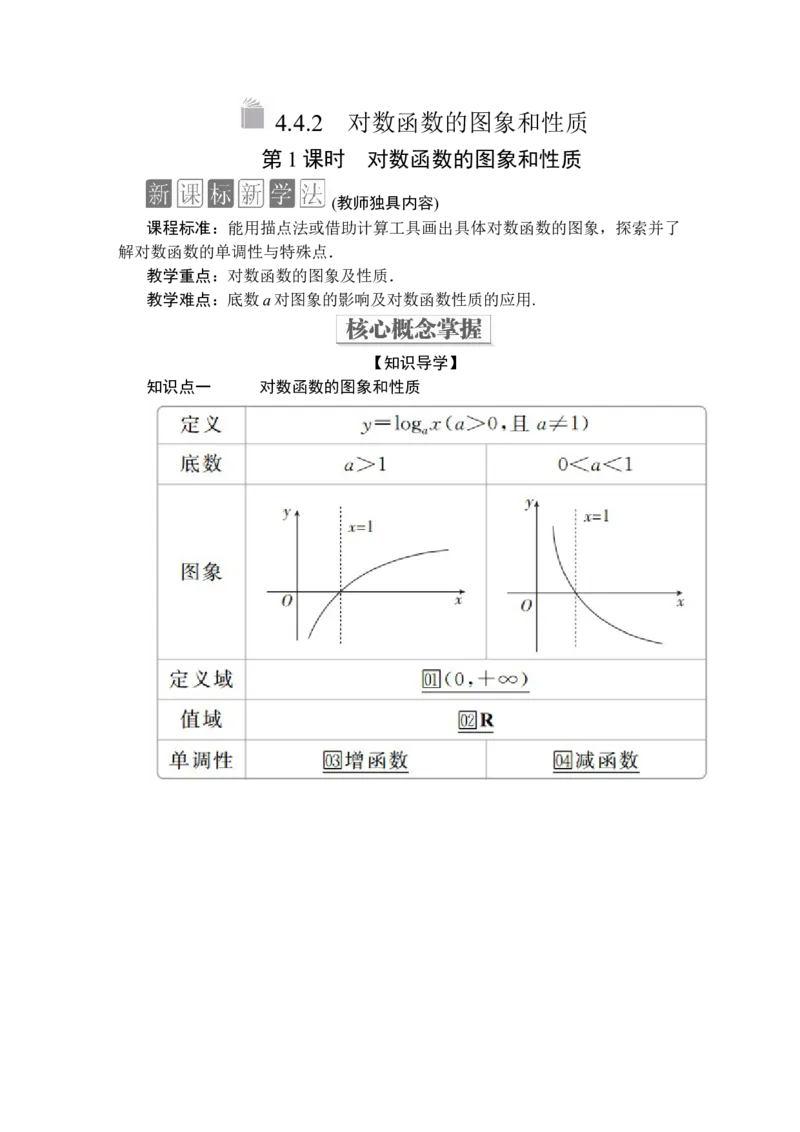
知识点一 对数函数的图象和性质知识点二 指数函数与对数函数的关系【新知拓展】
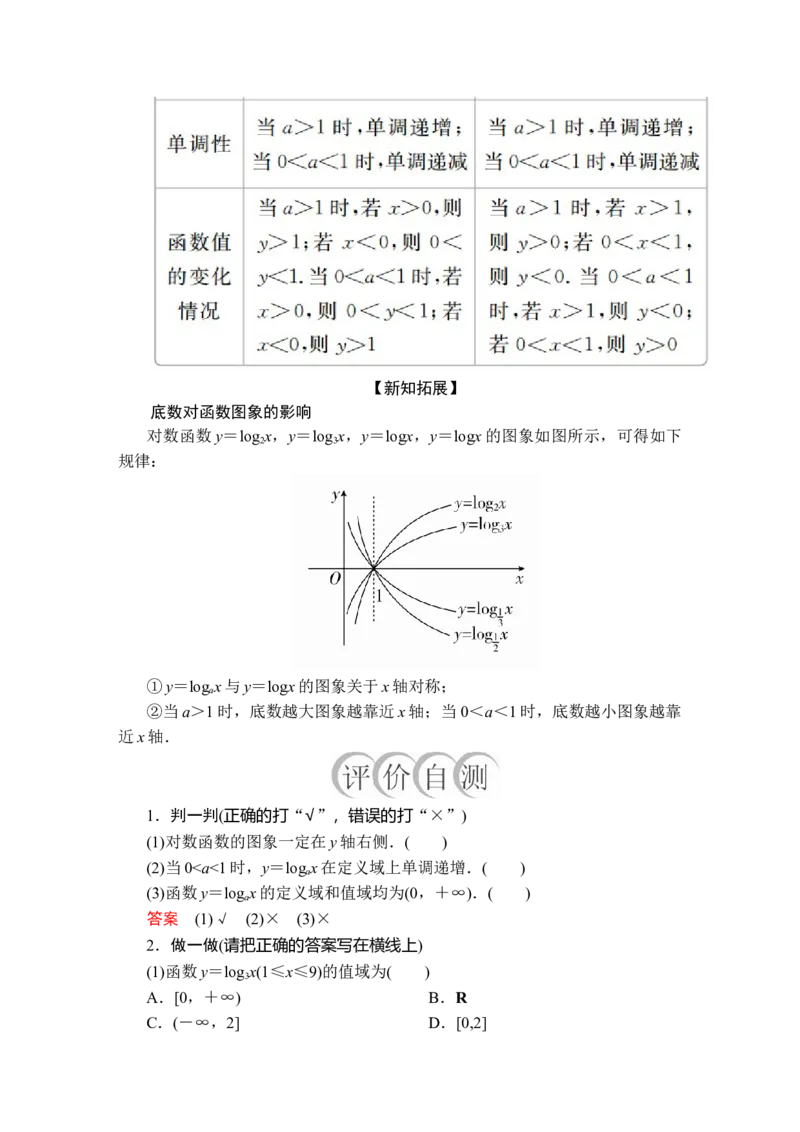
底数对函数图象的影响
对数函数y=log x,y=log x,y=logx,y=logx的图象如图所示,可得如下
2 3
规律:
①y=log x与y=logx的图象关于x轴对称;
a
②当a>1时,底数越大图象越靠近x轴;当0<a<1时,底数越小图象越靠
近x轴.
1.判一判(正确的打“√”,错误的打“×”)
(1)对数函数的图象一定在y轴右侧.( )
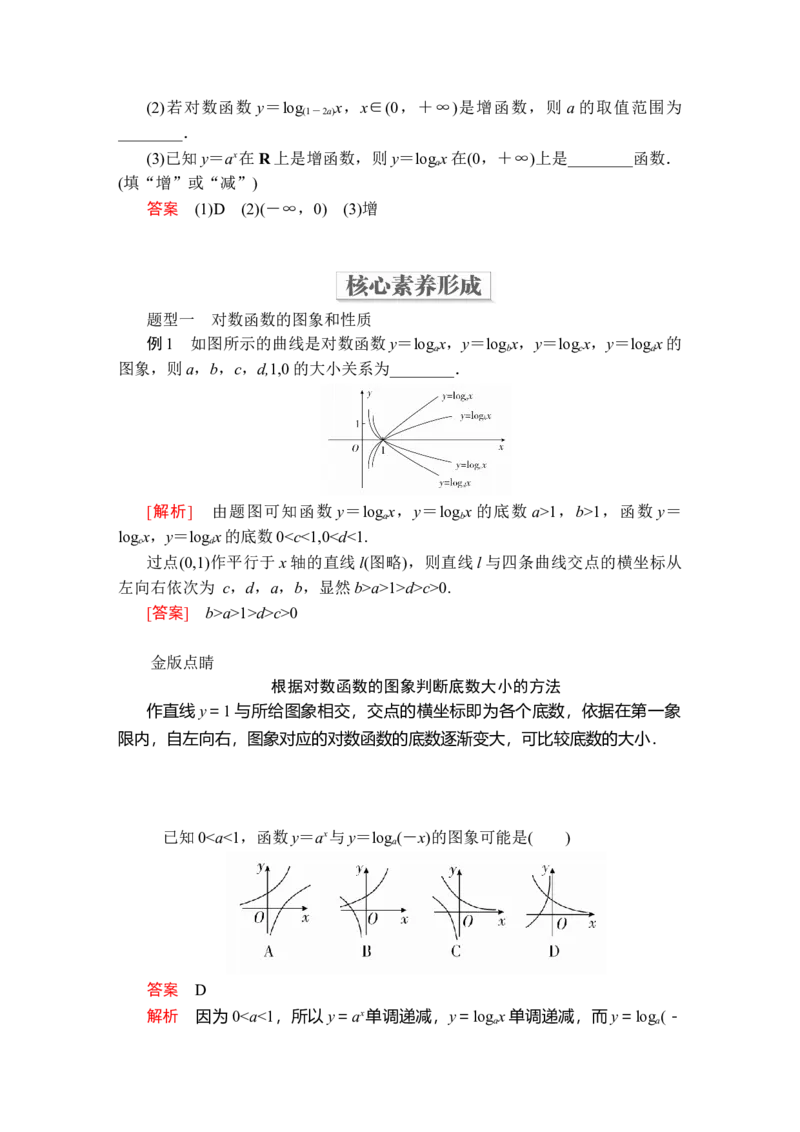
(2)当01,b>1,函数 y=
a b
log x,y=log x的底数0a>1>d>c>0.
[答案] b>a>1>d>c>0
金版点睛
根据对数函数的图象判断底数大小的方法
作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象
限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.
已知00,且a≠1)的图象恒过定点(3,2),则实数
a
b,c的值分别为_______.
[解析] ∵函数的图象恒过定点(3,2),∴将(3,2)代入y=log (x+b)+c,得2=
a
log (3+b)+C.又当a>0,且a≠1时,log 1=0恒成立,∴c=2,由log (3+b)=
a a a
0,得3+b=1,∴b=-2.故填-2,2.
[答案] -2,2
金版点睛
画对数函数图象时要注意的问题
(1)明确对数函数图象的分布区域.对数函数的图象在第一、四象限.当 x趋
近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)建立分类讨论的思想.在画对数函数图象之前要先判断对数的底数 a的取
值范围是a>1,还是00,且a≠1)的图象经过点:(1,0),(a,1)
a
和.
函数y=log (x+1)-2(a>0,且a≠1)的图象恒过点________.
a
答案 (0,-2)
解析 因为函数y=log x(a>0,且a≠1)的图象恒过点(1,0),则令x+1=1,
a
得x=0,此时y=log (x+1)-2=-2,所以函数y=log (x+1)-2(a>0,且a≠1)
a a
的图象恒过点(0,-2).
题型二 对数式的大小比较
例3 比较下列各组中两个值的大小:
(1)log 1.9,log 2;
3 3
(2)log 3,log 2;
2 0.3
(3)log π,log 3.14(a>0,a≠1).
a a
[解] (1)因为y=log x在(0,+∞)上是增函数,所以log 1.9log 1=0,log 2log 2.
2 2 0.3 0.3 2 0.3
(3)当a>1时,函数y=log x在(0,+∞)上是增函数,则有log π>log 3.14;
a a a
当01时,log π>log 3.14;当0.
比较下列各组中两个值的大小:
(1)3log 5,2log 3;
4 2
(2)log 0.2,log 0.2;
3 4
(3)log π,log 3;
3 π
(4)log 0.1,0.20.1.
0.2
解 (1)∵3log 5=log 125,2log 3=log 9=log 81,且函数y=log x在(0,+∞)
4 4 2 2 4 4
上是增函数,又125>81,∴3log 5>2log 3.
4 2
(2)∵0>log 3>log 4,∴<,
0.2 0.2
即log 0.23,∴log π>log 3=1.
3 3 3
同理,1=log π>log 3,所以log π>log 3.
π π 3 π
(4)∵函数y=log x在(0,+∞)上是减函数,且0.1<0.2,∴log 0.1>log 0.2=
0.2 0.2 0.2
1.
∵函数y=0.2x在R上是减函数,且0<0.1,
∴0.20.1<0.20=1.
∴log 0.1>0.20.1.
0.2
题型三 与对数有关的函数的值域问题
例4 求下列函数的值域:
(1)y=log (x2+4);(2)y=log (3+2x-x2).
2[解] (1)y=log (x2+4)的定义域是R.
2
因为x2+4≥4,所以log (x2+4)≥log 4=2.
2 2
所以y=log (x2+4)的值域为[2,+∞).
2
(2)设u=3+2x-x2=-(x-1)2+4≤4.
因为u>0,所以00,且a≠1的复合函数,其值域的求解步骤如下:
a
①分解成y=log u,u=fx两个函数;
a
②求fx的定义域;
③求u的取值范围;
④利用y=log u的单调性求解.
a
函数y=lg (1+32-x2)的值域为( )
A.(-∞,1) B.(0,1]
C.[0,+∞) D.(1,+∞)
答案 B
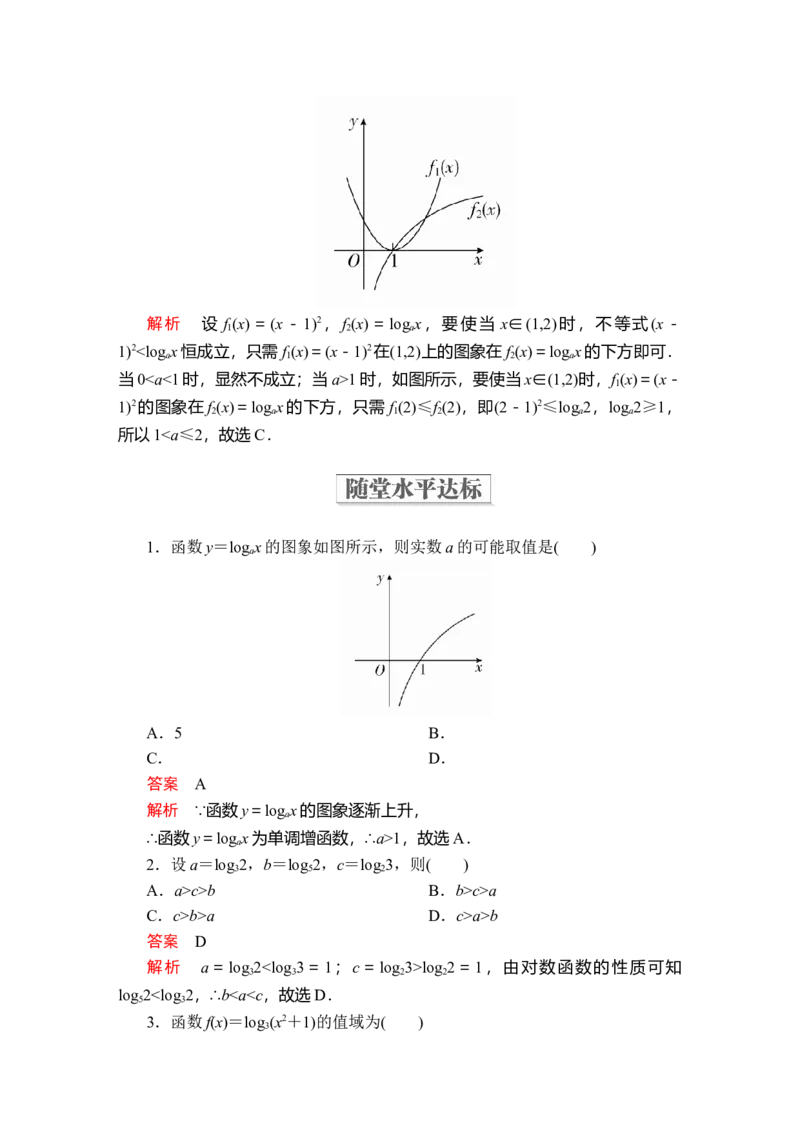
解析 ∵2-x2≤2,∴0<32-x2≤9,∴1<1+32-x2≤10,∴01时,如图所示,要使当x∈(1,2)时,f (x)=(x-
1
1)2的图象在f (x)=log x的下方,只需f (2)≤f (2),即(2-1)2≤log 2,log 2≥1,
2 a 1 2 a a
所以11,故选A.
a
2.设a=log 2,b=log 2,c=log 3,则( )
3 5 2
A.a>c>b B.b>c>a
C.c>b>a D.c>a>b
答案 D
解析 a=log 2log 2=1,由对数函数的性质可知
3 3 2 2
log 20,且a≠1)的图象恒过定点 P,则点P
a
的坐标是________.
答案 (2,2)
解析 令x-1=1,得x=2,即f(2)=2,故P(2,2).
5.若函数f(x)为定义在R上的奇函数,且x∈(0,+∞)时,f(x)=lg (x+1),
求f(x)的表达式,并画出大致图象.
解 ∵f(x)为R上的奇函数,∴f(0)=0.
又当x∈(-∞,0)时,-x∈(0,+∞),
∴f(-x)=lg (1-x).
又f(-x)=-f(x),
∴f(x)=-lg (1-x),
∴f(x)的解析式为
f(x)=
f(x)的大致图象如图所示.