文档内容
A级:“四基”巩固训练
一、选择题
1.下列函数中,增长速度最慢的是( )
A.y=6x B.y=log x
6
C.y=x6 D.y=6x
答案 B
解析 增长速度最慢的是对数函数y=log x.
6
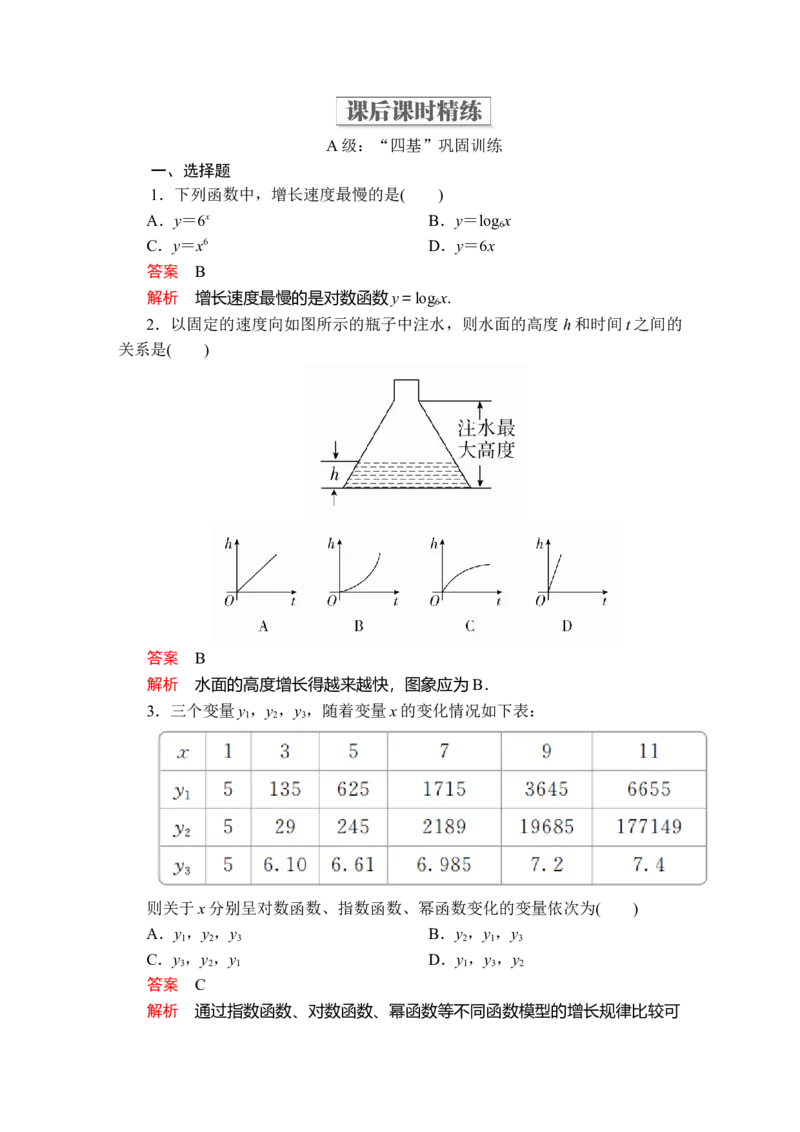
2.以固定的速度向如图所示的瓶子中注水,则水面的高度 h和时间t之间的
关系是( )
答案 B
解析 水面的高度增长得越来越快,图象应为B.
3.三个变量y ,y ,y ,随着变量x的变化情况如下表:
1 2 3
则关于x分别呈对数函数、指数函数、幂函数变化的变量依次为( )
A.y ,y ,y B.y ,y ,y
1 2 3 2 1 3
C.y ,y ,y D.y ,y ,y
3 2 1 1 3 2
答案 C
解析 通过指数函数、对数函数、幂函数等不同函数模型的增长规律比较可知,对数函数的增长速度越来越慢,变量 y 随x的变化符合此规律;指数函数的
3
增长速度最快,y 随x的变化符合此规律;幂函数的增长速度介于指数函数与对
2
数函数之间,y 随x的变化符合此规律,故选C.
1
4.在一次数学试验中,采集到如下一组数据:
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+
答案 B
解析 ∵x=0时,无意义,∴D不成立;由对应数据显示该函数是增函数,
且增幅越来越快,∴A不成立;∵C是偶函数,∴x=±1的值应该相等,故C不成
立;对于B,当x=0时,y=1,∴a+1=1,a=0;当x=1时,y=a+b=2.02,
∴b=2.02,经验证,它与各数据比较接近.
5.若x∈(1,2),则下列结论正确的是( )
答案 A
解析 ∵x∈(1,2),∴2x>2,x∈(1,),lg x∈(0,1),∴2x>x>lg x.故选A.
6.某地为加强环境保护,决定使每年的绿地面积比上一年增长 10%,那么
从今年起,x年后绿地面积是今年的y倍,则函数y=f(x)的大致图象是( )
答案 D
解析 设今年绿地面积为m,则有my=(1+10%)xm,∴y=1.1x,故选D.
二、填空题
7.若a>1,n>0,那么当x足够大时,ax,xn,log x中最大的是________.
a
答案 ax解析 ∵a>1,n>0,∴函数y =ax,y =xn,y =log x都是增函数.由指数
1 2 3 a
函数、对数函数、幂函数的变化规律可知,当x足够大时,ax>xn>log x.
a
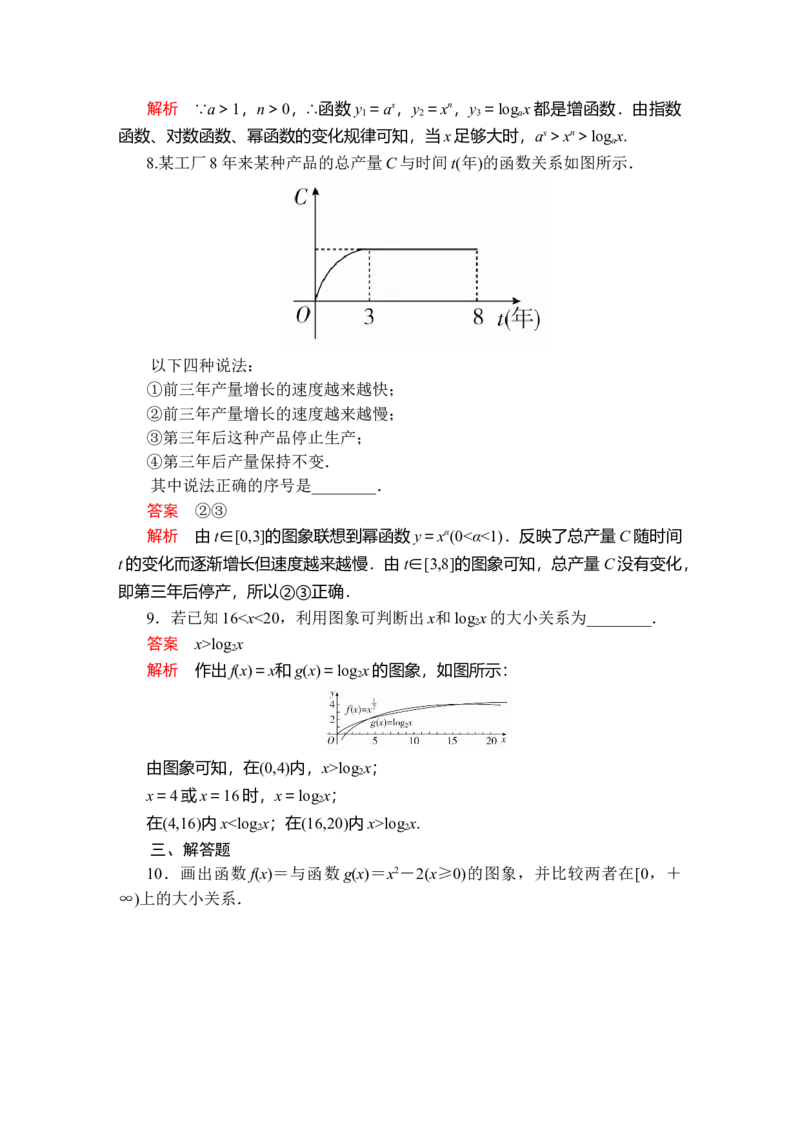
8.某工厂8年来某种产品的总产量C与时间t(年)的函数关系如图所示.
以下四种说法:
①前三年产量增长的速度越来越快;
②前三年产量增长的速度越来越慢;
③第三年后这种产品停止生产;
④第三年后产量保持不变.
其中说法正确的序号是________.
答案 ②③
解析 由t∈[0,3]的图象联想到幂函数y=xα(0<α<1).反映了总产量C随时间
t的变化而逐渐增长但速度越来越慢.由t∈[3,8]的图象可知,总产量C没有变化,
即第三年后停产,所以②③正确.
9.若已知16log x
2
解析 作出f(x)=x和g(x)=log x的图象,如图所示:
2
由图象可知,在(0,4)内,x>log x;
2
x=4或x=16时,x=log x;
2
在(4,16)内xlog x.
2 2
三、解答题
10.画出函数 f(x)=与函数g(x)=x2-2(x≥0)的图象,并比较两者在[0,+
∞)上的大小关系.解 函数f(x)与g(x)的图象如图所示.
根据图象易得:
当0≤x<4时,f(x)>g(x);
当x=4时,f(x)=g(x);
当x>4时,f(x)<g(x).
B级:“四能”提升训练
1.生活经验告诉我们,当水注入容器(设单位时间内进水量相同)时,容器
内水面的高度随着时间的变化而变化,在图中请选择与容器相匹配的图象,A对
应________;B对应________;C对应________;D对应________.
答案 (4) (1) (3) (2)
解析 A容器下粗上细,水高度的变化先慢后快,故与(4)对应;B容器为球
形,水高度变化为快—慢—快,应与(1)对应;C,D容器都是柱形的,水高度的
变化速度都应是直线型,但C容器细,D容器粗,故水高度的变化为:C容器快,
与(3)对应,D容器慢,与(2)对应.
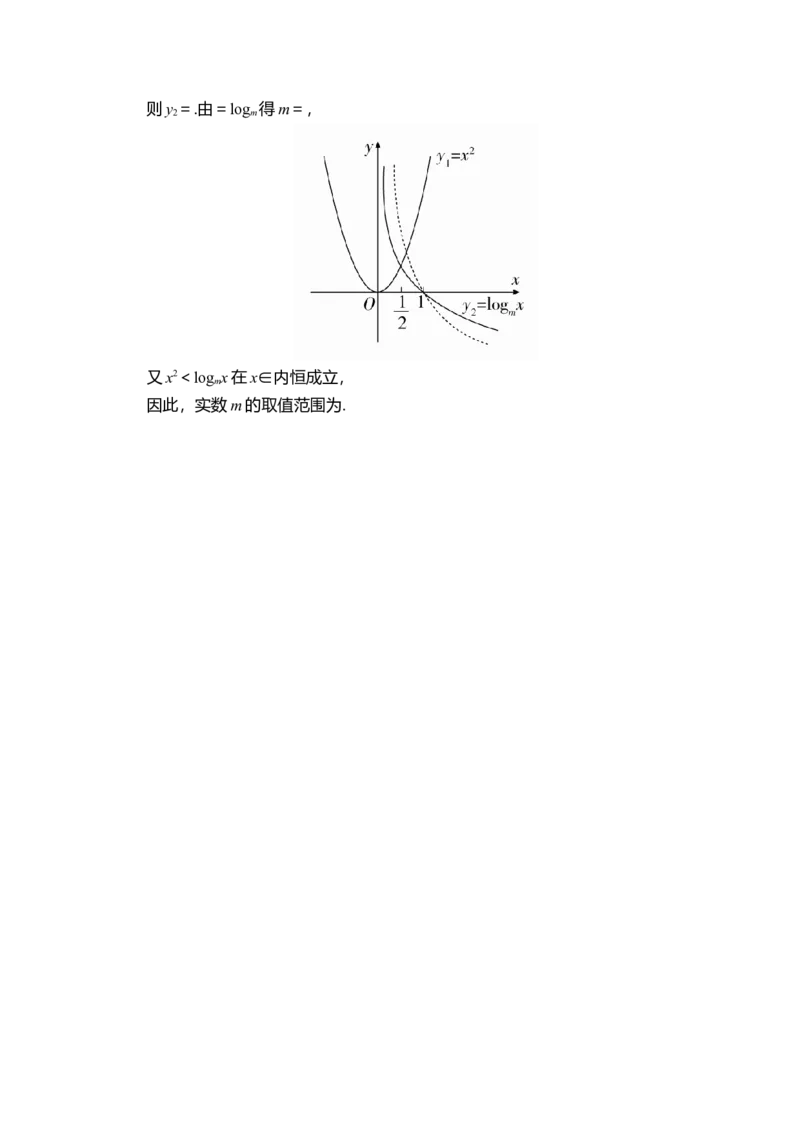
2.若x2<log x在x∈内恒成立,求实数m的取值范围.
m
解 设y =x2,y =log x,作出符合题意的两函数的大致图象(如图),可知0
1 2 m
<m<1.
当x=时,y =,若两函数图象在x=处相交,
1则y =.由=log 得m=,
2 m
又x2<log x在x∈内恒成立,
m
因此,实数m的取值范围为.