文档内容
A级:“四基”巩固训练
一、选择题
1.如果logx0,且a≠1),则实数a的取值范围为( )
a
A. B.
C.∪(1,+∞) D.∪
答案 C
解析 log <1=log a,当01时,a>,即a>1.综
a a
上,a∈∪(1,+∞).
3.已知函数y=ex的图象与函数y=f(x)的图象关于直线y=x对称,则( )
A.f(2x)=e2x(x∈R)
B.f(2x)=ln 2·ln x(x>0)
C.f(2x)=2ex(x∈R)
D.f(2x)=ln x+ln 2(x>0)
答案 D
解析 因为函数y=ex的图象与函数f(x)的图象关于直线y=x对称,所以f(x)
是y=ex的反函数,即f(x)=ln x,故f(2x)=ln 2x=ln x+ln 2(x>0),故选D.
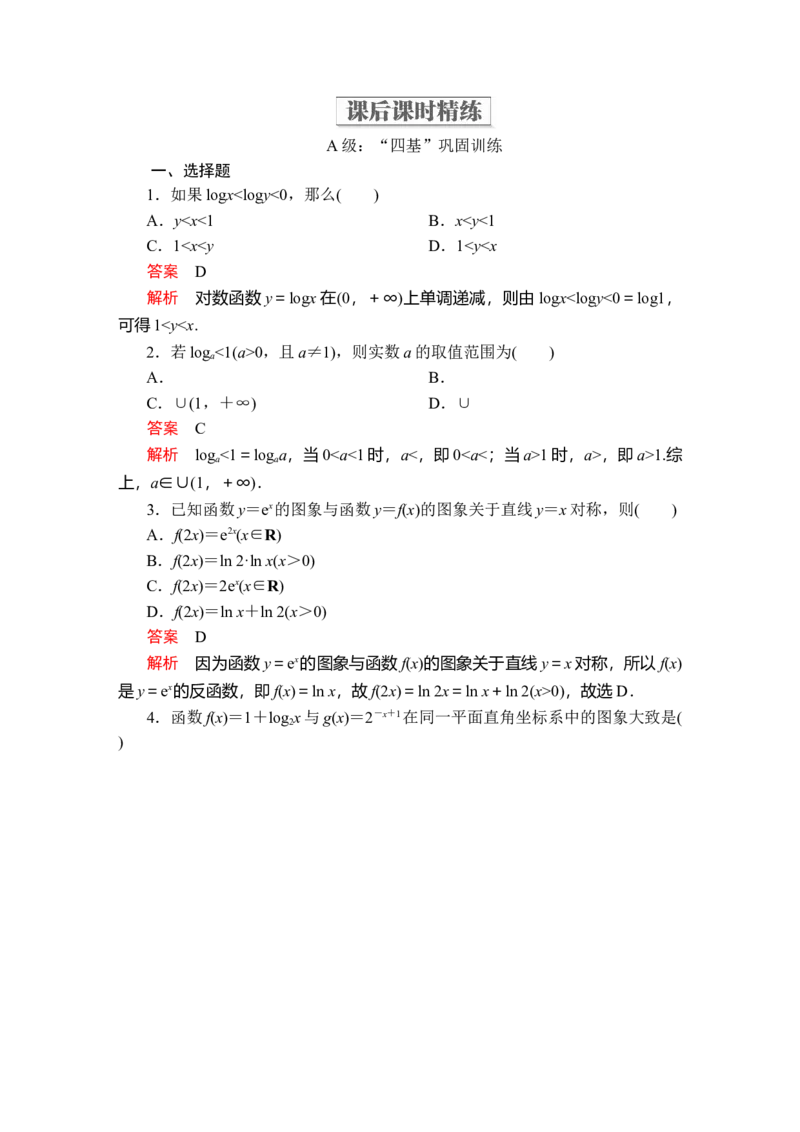
4.函数f(x)=1+log x与g(x)=2-x+1在同一平面直角坐标系中的图象大致是(
2
)答案 C
解析 f(x)=1+log x的图象是由y=log x的图象向上平移一个单位长度得到
2 2
的,过定点(1,1),g(x)=2-x+1=x-1的图象是由y=x的图象向右平移一个单位长度
得到的,过定点(0,2),故只有C项中的图象符合.
5.函数f(x)=若f(a)>f(-a),则实数a的取值范围是( )
A.(-1,0)∪(0,1) B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1)
答案 C
解析 若a>0,由f(a)>f(-a),得log a>loga=-log a,即log a>0,则a>1;
2 2 2
若 a<0,则由 f(a)>f(-a),得 log (-a)>log (-a),即-log (-a)>log (-a),则
2 2 2
log (-a)<0,得0<-a<1,即-10,∴f(x)=log ·log(2x)=log x·log (4x2)=log x·(log 4+2log x)=
2 2 2 2 2 2
log x+(log x)2=2-≥-,当且仅当x=时,有f(x) =-.
2 2 min
三、解答题
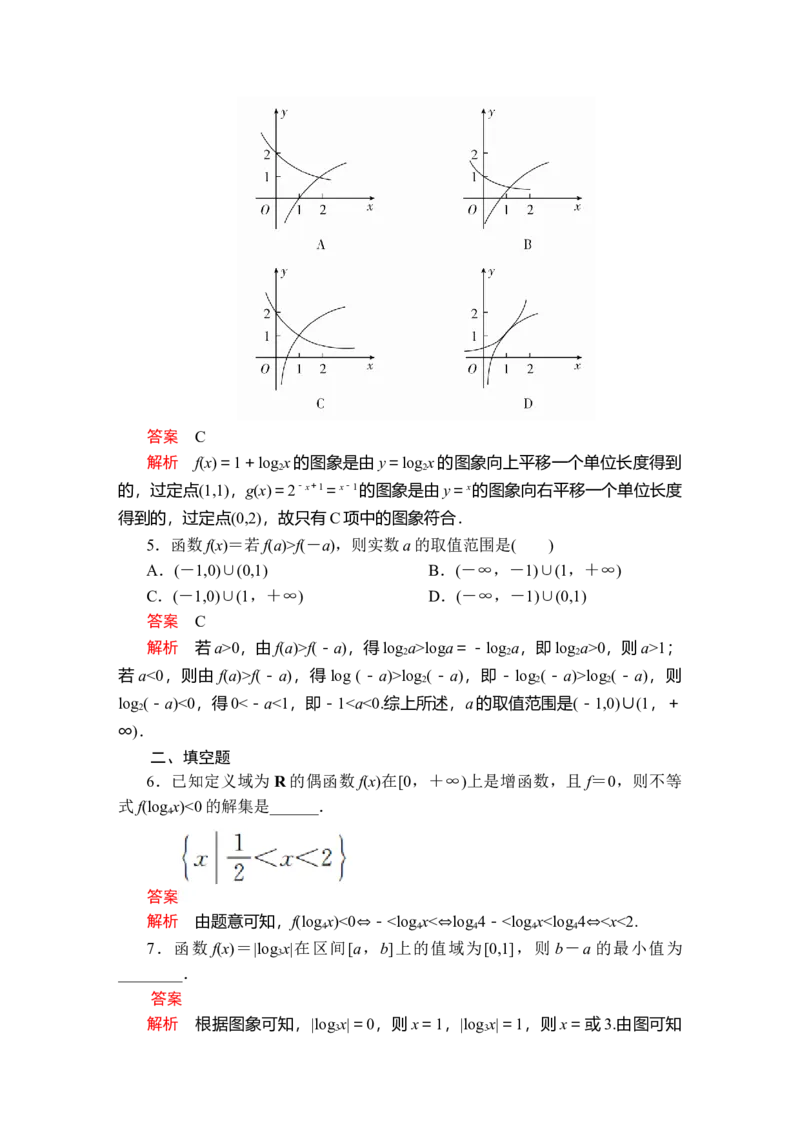
9.函数f(x)=-log ,x∈(0,1),求不等式f(x2)>f的解集.
3
解 ∵y=在(0,1)上为减函数,
y=-log =log =log 在(0,1)上也为减函数,
3 3 3
∴f(x)=-log 在(0,1)上单调递减.
3
∴x2<.∴0