文档内容
秘密★启⽤前
2024-2025(下)期末质量监测
⾼ ⼀ 数 学
本试卷满分150分 考试时间120分钟
【命题组织单位:辽宁沈⽂新⾼考研究联盟】
第Ⅰ卷 选择题(共 58分)
⼀、单选题(本⼤题共8⼩题,每⼩题5分,共40分,在每⼩题所给的四个选项中,有且只
有⼀项是符合题⽬要求的)
1.如果复数 满⾜ ,那么 的最⼩值是
A. B. C. D.
2.已知点 在第三象限,则⻆ 的终边在第⼏象限
A.第⼀象限 B.第⼆象限 C.第三象限 D.第四象限
3.已知 ,则“ ” 是“ , ” 的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知点 , , ,则 在 上的投影向量的坐标为
A. B. C. D.
5.如图,已知正六边形 ,下列向量的数量积中最⼤的是
A. B. C. D.
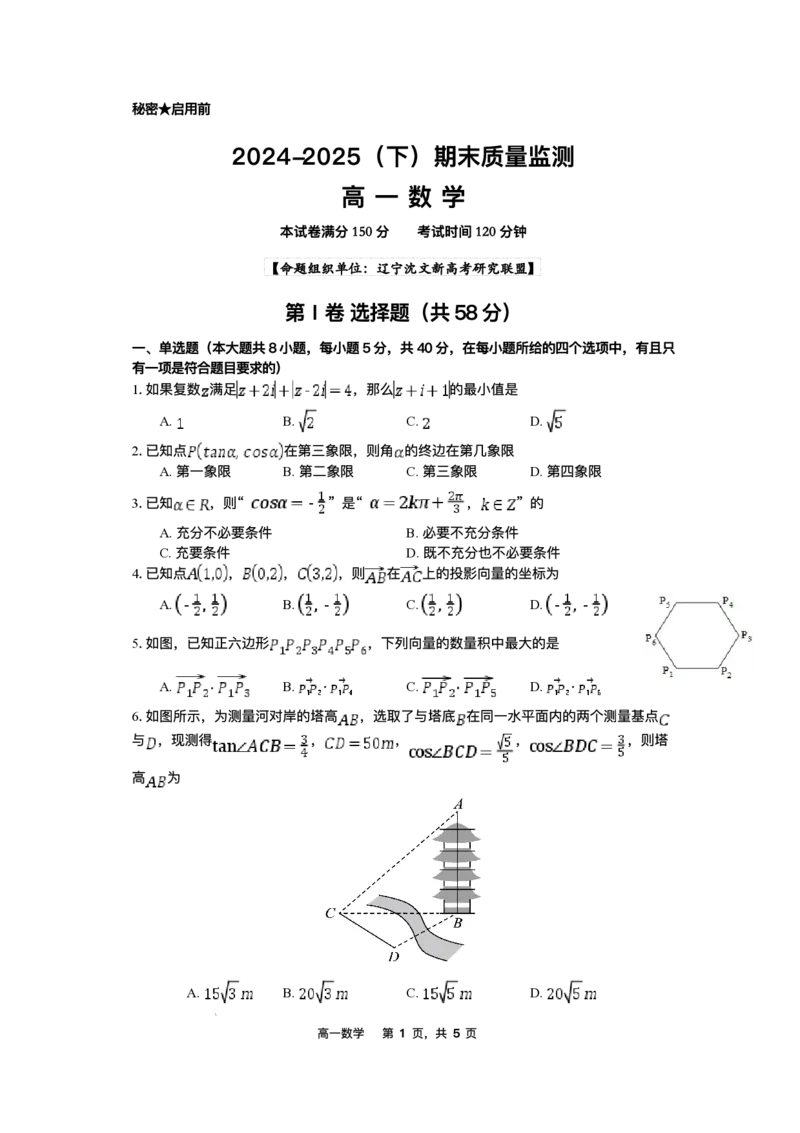
6.如图所示,为测量河对岸的塔⾼ ,选取了与塔底 在同⼀⽔平⾯内的两个测量基点
与 ,现测得 , , , ,则塔
⾼ 为
A. B. C. D.
⾼⼀数学 第 1 ⻚,共 5 ⻚
学科⽹(北京)股份有限公司7.在空间中, , 是不重合的直线, , 是不重合的平⾯,则下列说法正确的是
A.若 , , ,则
B.若 , ,则
C.若 , , ,则
D.若 , , ,则
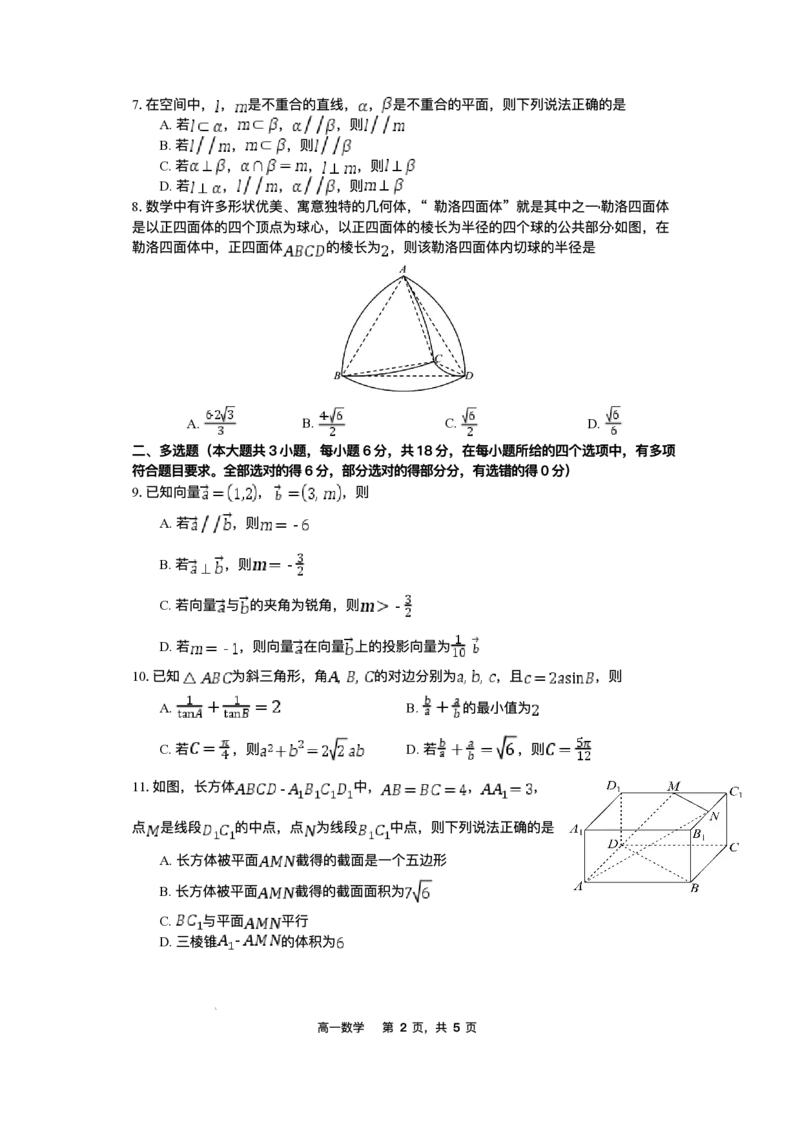
8.数学中有许多形状优美、寓意独特的⼏何体,“ 勒洛四⾯体” 就是其中之⼀勒洛四⾯体
是以正四⾯体的四个顶点为球⼼,以正四⾯体的棱⻓为半径的四个球的公共部分如图,在
勒洛四⾯体中,正四⾯体 的棱⻓为 ,则该勒洛四⾯体内切球的半径是
A. B. C. D.
⼆、多选题(本⼤题共3⼩题,每⼩题6分,共18分,在每⼩题所给的四个选项中,有多项
符合题⽬要求。全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.已知向量 , ,则
A.若 ,则
B.若 ,则
C.若向量 与 的夹⻆为锐⻆,则
D.若 ,则向量 在向量 上的投影向量为
10.已知 为斜三⻆形,⻆ 的对边分别为 ,且 ,则
A. B. 的最⼩值为
C.若 ,则 D.若 ,则
11.如图,⻓⽅体 中, , ,
点 是线段 的中点,点 为线段 中点,则下列说法正确的是
A.⻓⽅体被平⾯ 截得的截⾯是⼀个五边形
B.⻓⽅体被平⾯ 截得的截⾯⾯积为
C. 与平⾯ 平⾏
D.三棱锥 的体积为
⾼⼀数学 第 2 ⻚,共 5 ⻚
学科⽹(北京)股份有限公司第Ⅱ卷 ⾮选择题(共 92分)
三、填空题(本⼤题共3⼩题,每⼩题5分,共15分)
12.已知 ,则 .
13.已知平⾯单位向量 , 满⾜ 设 , ,向量 ,
的夹⻆为 ,则 的最⼩值是 .
14.已知 三边分别为 ,且 则边 所对应的⻆ ⼤⼩为 ,
此时,如果 ,则 的最⼤值为 .
四、解答题(本⼤题共5⼩题,共77分。解答时应写出必要的⽂字说明、证明过程或演算步
骤)
15.已知 , .
求 的值;
求 的值.
16.在 中,⻆ , , 所对的边分别为 , , ,满⾜
.
求 的⼤⼩;
若 , 的⾯积为 ,求 的周⻓.
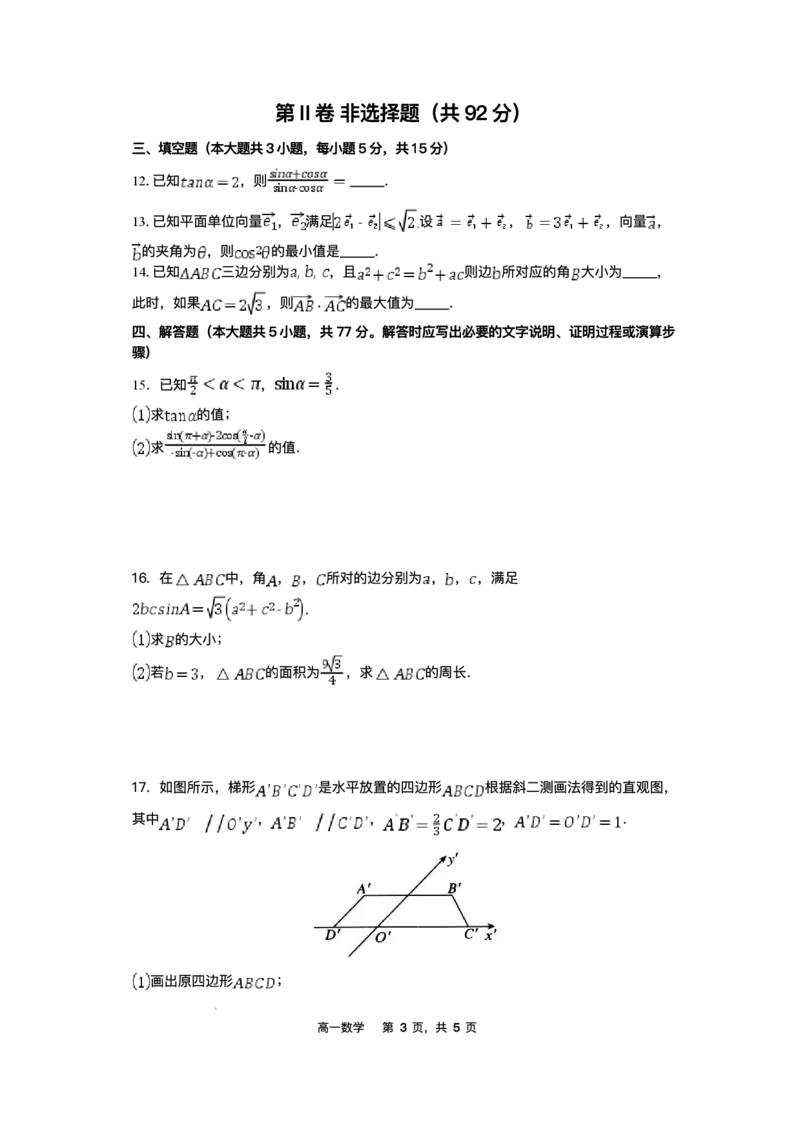
17.如图所示,梯形 是⽔平放置的四边形 根据斜⼆测画法得到的直观图,
其中 , , , .
画出原四边形 ;
⾼⼀数学 第 3 ⻚,共 5 ⻚
学科⽹(北京)股份有限公司分别求出原四边形 与梯形 的⾯积.
18.在平⾯直⻆坐标系中, 为坐标原点, , , 三点共线,点 不在直线 上,满
⾜ .
求 的值;
, , , ,若
的最⼩值为 ,求 的最⼤值.
19.
材料⼀:
我们可以发现这样⼀个现象:随机⽣成的⼀元多项式,在复数集中最终都可以分解成
⼀次因式的乘积,且⼀次因式的个数 包括重复因式 就是被分解的多项式的次数事实上,
数学中有如下定理:
代数基本定理:任何⼀元 次复系数多项式⽅程 ⾄少有⼀个复数
根.
材料⼆:
由代数基本定理可以得到:任何⼀元 次复系数多项式 在复数集中可
以分解为 个⼀次因式的乘积进⽽,⼀元 次多项式⽅程有 个复数根 重根按重数计 .
下⾯我们从代数基本定理出发,看看⼀元多项式⽅程的根与系数之间的关系.
设实系数⼀元⼆次⽅程
在复数集 内的根为 ,容易得到
设实系数⼀元三次⽅程
在 复 数 集 内 的 根 为 , 可 以 得 到 , ⽅ 程 可 变 形 为
展开得:
⽐较 可以得到根与系数之间的关系:
阅读以上材料,利⽤材料中的⽅法及学过的知识解决下列问题:
对于⽅程 在复数集 内的根为 ,求 的值;
⾼⼀数学 第 4 ⻚,共 5 ⻚
学科⽹(北京)股份有限公司如果实系数⼀元四次⽅程 在复数集 内的
根为 ,试找到根与系数之间的关系;
已知函数 ,对于⽅程 在复数集 内的根为 ,
当 时,求 的最⼤值.
⾼⼀数学 第 5 ⻚,共 5 ⻚
学科⽹(北京)股份有限公司2024-2025(下)期末质量监测
⾼ ⼀ 数 学 参考答案
【命题组织单位:辽宁沈⽂新⾼考研究联盟】
1 2 3 4 5 6 7 8 9 10 11
A B B C A C D B BD AC ABD
12.3
13.
14.
15.解: 因为 ,则 ,⼜ ,
所以 ,则 .
所以 .
原式 .
16.解: 因为 ,
所以 ,
由余弦定理得, ,
由正弦定理得 ,
因为 ,所以 ,
所以 ,即 ,
⼜ ,所以 .
因为 ,所以 ,
由余弦定理得, ,
因为 ,所以 ,解得 ,
所以 的周⻓为 .
17.解: 如图,建⽴平⾯直⻆坐标系 ,
⾼⼀数学答案 第 1 ⻚,共 3 ⻚
学科⽹(北京)股份有限公司在 轴上截取 , .
在过点 的 轴的平⾏线上截取 .
在过点 的 轴的平⾏线上截取 ,连接 ,
即可得到原四边形 .
原四边形 是直⻆梯形,且 , , .
所以其⾯积为 .
易得直观图中梯形的⾼为 ,
⼜ , ,
所以其⾯积为 .
18.解: 由题意,因为 三点共线,则 ,
则有 ,
由题意, 不共线,⽽ ,
于是 ,解得 ,
从⽽ 的值为 .
由题意,知 , ,
,
,
函数
,
令 ,因为 ,所以 ,
令 , .
当 时, 的最⼩值为 ,即
当 时, 的最⼩值为 ,即
当 时, 的最⼩值为 ,即 .
⾼⼀数学答案 第 2 ⻚,共 3 ⻚
学科⽹(北京)股份有限公司综上所述,
可得 的最⼤值为 ,即 的最⼤值为 .
19.解:
由阅读材料可知: ,且
有: ;
由材料可知:⼀元四次⽅程可改写为
展开得:
故可得:
由题有 的三个实根为 .
设 ,
展开得 ,
故 ,
则 ,
⼜ ,故 ,
综上:当 时, 的最⼤值为 ;
注:具体评分变更信息(分值、答案等)请阅卷教师关注阅卷群。
⾼⼀数学答案 第 3 ⻚,共 3 ⻚
学科⽹(北京)股份有限公司