文档内容
第 2 课时 指数函数的图象和性质的应用
(教师独具内容)
课程标准:1.掌握指数函数的图象变换.2.熟悉指数函数与其他函数的复合函
数的处理方法.3.熟悉指数函数在实际问题中的应用.
教学重点:1.指数函数的图象与底数的关系.2.指数函数的图象变换与参数的
关系,特殊点在图象变换中的作用.3.复合函数的单调性、定义域与值域问题的处
理方法.4.指数函数性质的应用.
教学难点:1.指数函数的图象与底数关系的直观理解与严格证明.2.参数在图
象变换(平移、翻转)中的作用,数形结合方法的进一步渗透.3.复合函数相关问题
中各种函数性质的综合应用.
【知识导学】
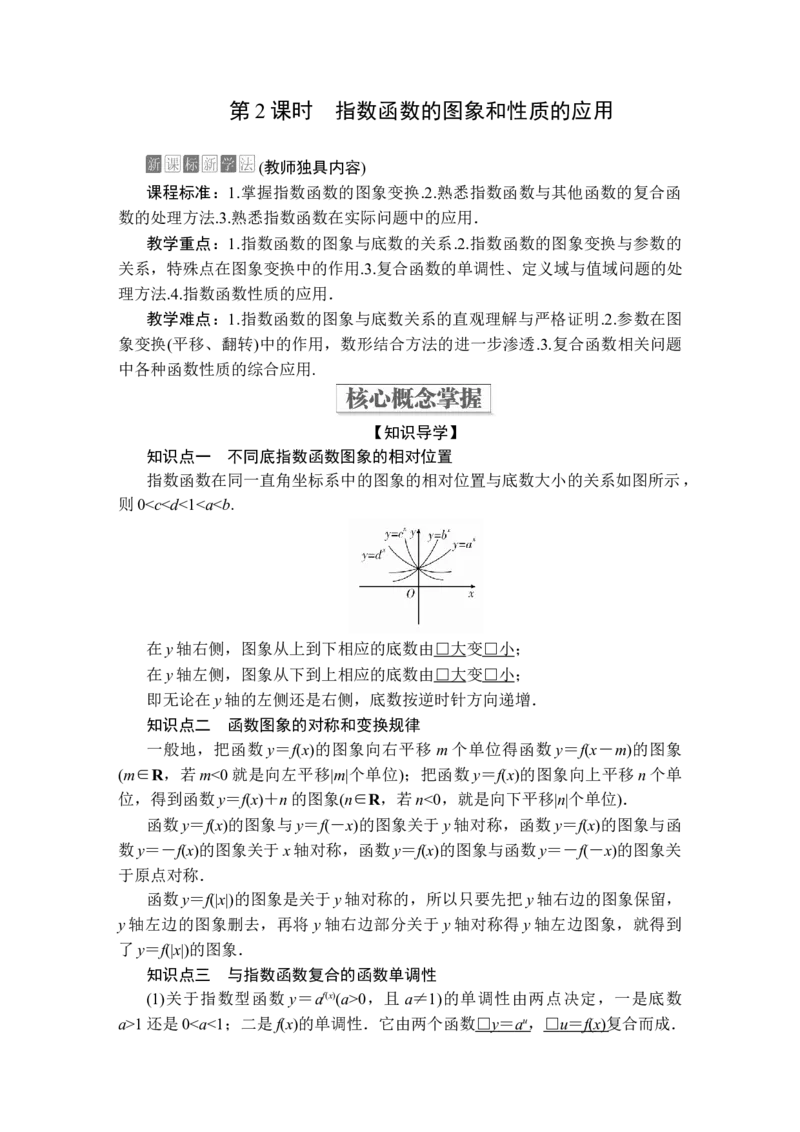
知识点一 不同底指数函数图象的相对位置
指数函数在同一直角坐标系中的图象的相对位置与底数大小的关系如图所示,
则00,且 a≠1)的单调性由两点决定,一是底数
a>1还是03-2.5.( )
(2)7-0.5<8-0.5.( )
(3)6-0.8<70.7.( )
答案 (1)√ (2)× (3)√
2.做一做(请把正确的答案写在横线上)
(1)如果a-5x>ax+7(a>0,且a≠1),当a>1时,x的取值范围是__________;当
016的x的取值范围是________.
(3)某种细菌在培养的过程中,每 15分钟分裂一次(由一个分裂成两个),则
这种细菌由一个分裂成4096个需经过________小时.
答案 (1) (2)(-∞,1)
(3)3题型一 指数函数的图象变换
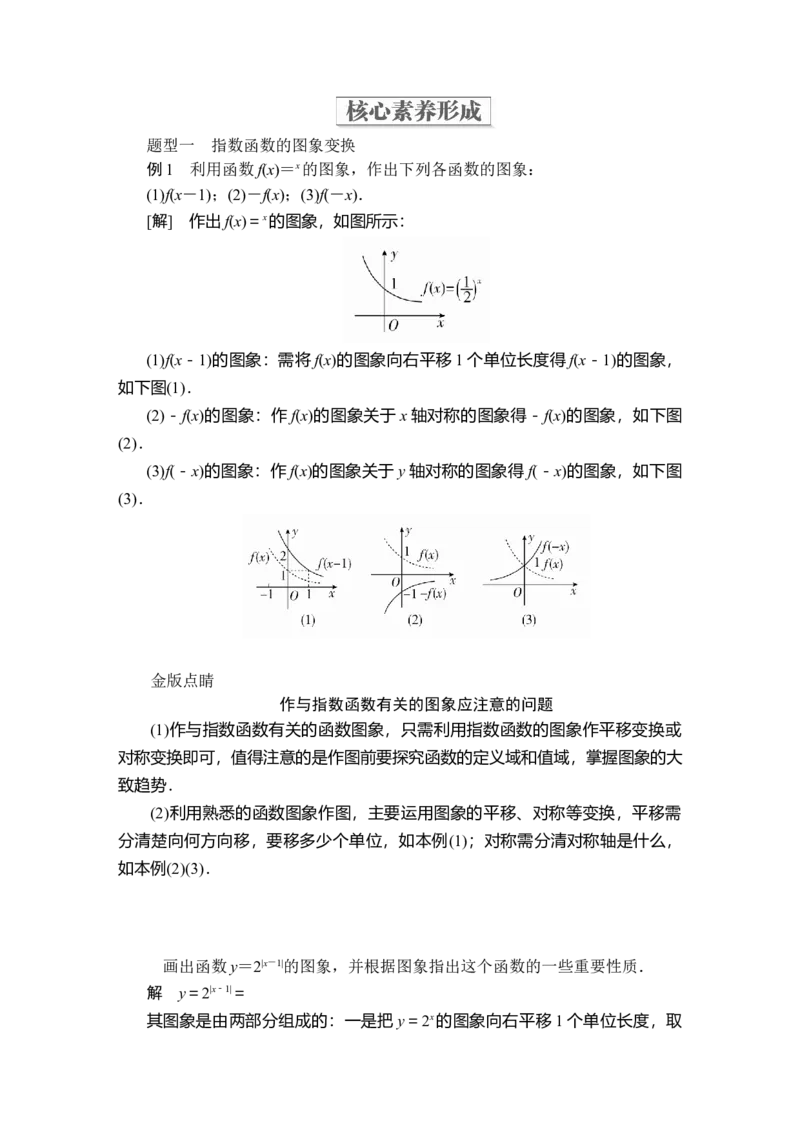
例1 利用函数f(x)=x的图象,作出下列各函数的图象:
(1)f(x-1);(2)-f(x);(3)f(-x).
[解] 作出f(x)=x的图象,如图所示:
(1)f(x-1)的图象:需将f(x)的图象向右平移1个单位长度得f(x-1)的图象,
如下图(1).
(2)-f(x)的图象:作f(x)的图象关于x轴对称的图象得-f(x)的图象,如下图
(2).
(3)f(-x)的图象:作f(x)的图象关于y轴对称的图象得f(-x)的图象,如下图
(3).
金版点睛
作与指数函数有关的图象应注意的问题
(1)作与指数函数有关的函数图象,只需利用指数函数的图象作平移变换或
对称变换即可,值得注意的是作图前要探究函数的定义域和值域,掌握图象的大
致趋势.
(2)利用熟悉的函数图象作图,主要运用图象的平移、对称等变换,平移需
分清楚向何方向移,要移多少个单位,如本例(1);对称需分清对称轴是什么,
如本例(2)(3).
画出函数y=2|x-1|的图象,并根据图象指出这个函数的一些重要性质.
解 y=2|x-1|=
其图象是由两部分组成的:一是把 y=2x的图象向右平移1个单位长度,取x≥1的部分;二是把y=x的图象向右平移1个单位长度,取x<1的部分,如图中
实线部分所示.由图象可知,函数有三个重要性质:
①对称性:图象的对称轴为直线x=1;
②单调性:在(-∞,1]上单调递减,在[1,+∞)上单调递增;
③函数的值域:[1,+∞).
题型二 利用指数函数的单调性比较大小
例2 比较下列各题中两个值的大小:
(1)1.7-2.5,1.7-3;(2)1.70.3,1.50.3;
(3)1.70.3,0.83.1.
[解] (1)∵1.7>1.
∴y=1.7x在(-∞,+∞)上是增函数.
∵-2.5>-3,∴1.7-2.5>1.7-3.
(2)解法一:∵1.7>1.5,
∴在(0,+∞)上,y=1.7x的图象位于y=1.5x的图象的上方.而0.3>0,
∴1.70.3>1.50.3.
解法二:∵1.50.3>0,且=0.3,
又>1,0.3>0,∴0.3>1,
∴1.70.3>1.50.3.
(3)∵1.70.3>1.70=1,0.83.1<0.80=1,
∴1.70.3>0.83.1.
金版点睛
比较函数值大小的常用方法
(1)利用函数单调性比较,此法用于可化为同底的式子.
(2)对于底数不同,指数相同的两个幂值比较大小,可利用指数函数的图象
的变化规律来判断.
(3)当底数不同,指数也不同时,采用中间值法,即当两个数不易比较时,
可找介于两值中间且与两数都能比较大小的一个值,进而利用中间值解决问题.比较下列各题中的两个值的大小.
(1)0.8-0.1,1.250.2;(2)-π,1.
解 (1)∵0<0.8<1,∴y=0.8x在R上是减函数.
∵-0.2<-0.1,∴0.8-0.2>0.8-0.1,
又∵0.8-0.2=1.250.2
∴0.8-0.1<1.250.2.
(2)∵0<<1,∴函数y=x在R上是减函数.
又∵-π<0,∴-π>0=1,即-π>1.
题型三 解简单的指数不等式
例3 设0a2x2+2x-3.
[解] ∵0a2x2+2x-3,
∴2x2-3x+2<2x2+2x-3,解得x>1.
∴不等式的解集是(1,+∞).
金版点睛
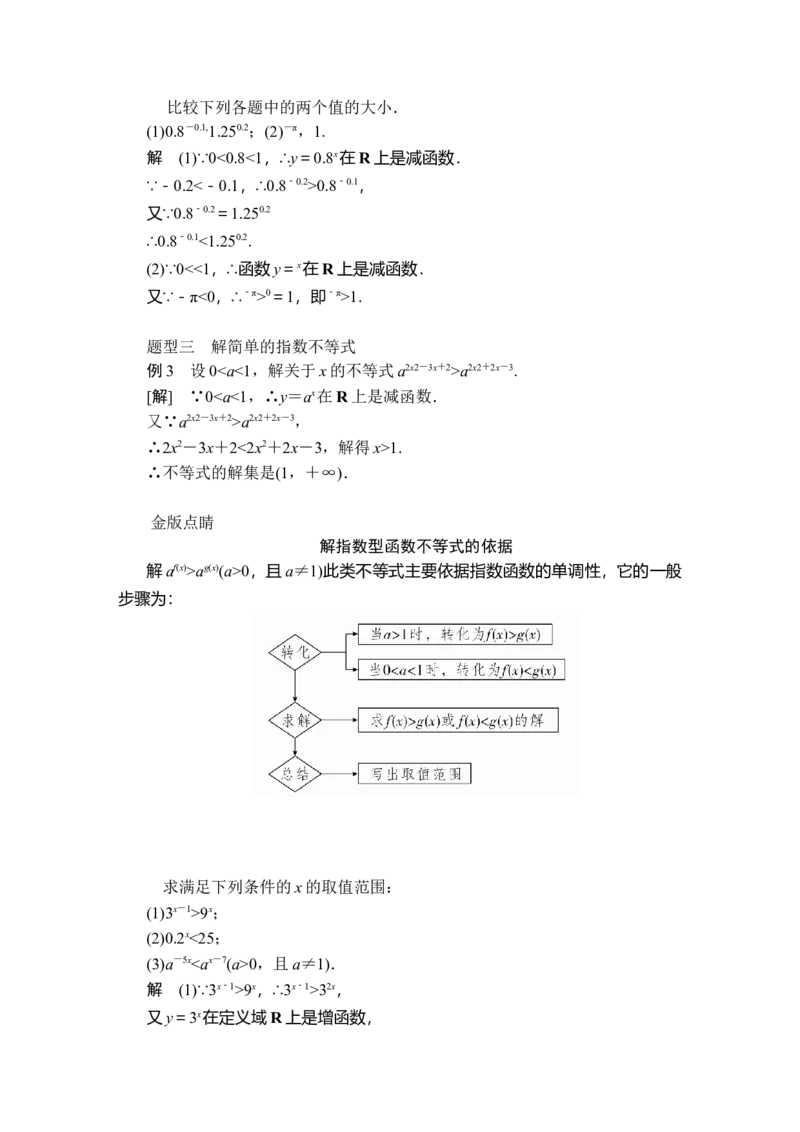
解指数型函数不等式的依据
解af(x)>ag(x)(a>0,且a≠1)此类不等式主要依据指数函数的单调性,它的一般
步骤为:
求满足下列条件的x的取值范围:
(1)3x-1>9x;
(2)0.2x<25;
(3)a-5x0,且a≠1).
解 (1)∵3x-1>9x,∴3x-1>32x,
又y=3x在定义域R上是增函数,∴x-1>2x,∴x<-1,
即x的取值范围是(-∞,-1).
(2)∵0<0.2<1,∴指数函数f(x)=0.2x在R上是减函数.
又25=0.2-2,∴0.2x<0.2-2,∴x>-2,即x的取值范围是(-2,+∞).
(3)当a>1时,∵a-5x;
当0x-7,
解得x<.
综上所述,当a>1时,x的取值范围是;当01时,函数y=f(ax)与函数f(x)的单调性相同;当02.53 B.0.82<0.83
C.π2<π D.0.90.3>0.90.5
答案 D
解析 因为函数y=0.9x在R上为减函数,所以0.90.3>0.90.5.
2.若2a+1<3-2a,则实数a的取值范围是( )
A.(1,+∞) B.
C.(-∞,1) D.
答案 B
解析 ∵函数y=x在R上为减函数,∴2a+1>3-2a,∴a>.
3.设<b0,且a≠1),当x≥0时,求函数f(x)的值域.
解 y=a2x+2ax-1,令t=ax,
则y=g(t)=t2+2t-1=(t+1)2-2.
当a>1时,∵x≥0,∴t≥1,
∴当a>1时,y≥2.
当01时,函数的值域是[2,+∞);
当0