文档内容
第二学期高一年级阶段数学检测
必修第四册学分认定考核试卷
说明:本试卷选择题(1-10题)为客观性试题(闭卷30分钟,共40分),填空题与四道大
题(11-19题)为主观性试题(开卷60分钟,共60分(其中含卷面书写分5分)),全卷共
100分;请将答案写在答题纸的相应位置上.
一、选择题:(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.请将正确答案填涂在答题纸上的相应位置)
1. 下面四个说法中,正确说法的个数为( )
(1)如果两个平面有三个公共点,那么这两个平面重合;
(2)两条直线可以确定一个平面;
(3)若 , , ,则 ;
(4)空间中,两两相交的三条直线在同一平面内.
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
【分析】
如果两个平面有三个公共点,那么这两个平面重合或者是相交,即可判断;利用两条异面直线不能确定一
个平面即可判断;利用平面的基本性质中的公理 判断即可;若两两相交的三条直线相交于同一点,则相
交于同一点的三直线不一定在同一平面内(如棱锥的3条侧棱),即可判断.
【详解】如果两个平面有三个公共点,那么这两个平面重合或者是相交,故(1)不正确;
两条异面直线不能确定一个平面,故(2)不正确;
利用平面的基本性质中的公理 判断(3)正确;
空间中,若两两相交的三条直线相交于同一点,则相交于同一点的三直线不一定在同一平面内(如棱锥的
3条侧棱),故(4)不正确,
综上所述只有一个说法是正确的,
故选:A.
【点睛】本题主要考查了空间中点,线,面的位置关系.属于较易题.
2. 设 是一条直线, 、 是两个不同的平面,则下列命题一定正确的是( )A. 若 , ,则
B. 若 , ,则
C. 若 , ,则
D. 若 , ,则
【答案】C
【解析】
【分析】
对于选项A:根据面面垂直的性质定理即可判断;对于选项 B:根据面面垂直的性质定理即可判断;对于
选项C:根据面面平行的性质定理判断即可;对于选项D:根据线面的位置关系判断即可.
【详解】对于选项A:若 , ,则 或 ,故A不正确;
对于选项B:若 , ,则 或 或 ,故B不正确;
对于选项C:若 , ,根据面面平行的性质定理可得 ,故C正确;
对于选项D:若 , ,则 或 ,故D不正确.
故选:C.
【点睛】本题主要考查了面面垂直的性质定理以及面面平行的性质定理.属于较易题.
3. 在 中, , , ,则 等于( )
A. B. 3 C. D. 21
【答案】A
【解析】
【分析】
直接根据余弦定理即可得出结果.
【详解】因为 , , ,所以 ,
即 ,
故选:A.
【点睛】本题主要考查了通过余弦定理解三角形,属于基础题.
4. 在 中,根据下列条件解三角形,其中有两个解的是( )
.
A , , B. , ,
C. , , D. , ,
【答案】D
【解析】
【分析】
在已知两边及一边对角用正弦定理解三角形时才可能出现两解.根据正弦定理判断.
【详解】A:已知两角和一边,三角形确定,只有一解;
B:已知两边及夹角用余弦定理,只有一解;
C:已知两边及一边对角,但已知的是大边所对的角,小边所对角只能是锐角,不可能有两解;
D: ,有两解.
故选:D.
【点睛】本题主要考查三角形解的个数问题,掌握正弦定理和余弦定理是解题关键.三角形解的个数中只
有在已知两边及一边对角用正弦定理解三角形时才可能出现两解,注意判断方法.属于较易题.
5. 若轴截面为正方形的圆柱的侧面积是S,则圆柱的体积为( )
A. B. C. D.
【答案】D
【解析】
【分析】
设出圆柱的高 ,找到侧面积 和 之间的关系,即可求得体积.
【详解】根据题意,不妨设圆柱的高为 ,又因为轴截面为正方形,
故可得底面半径为 .则 ,解得 ,
故可得圆柱体积 .
故选:D.
【点睛】本题考查圆柱的侧面积和体积的求解,属基础题.
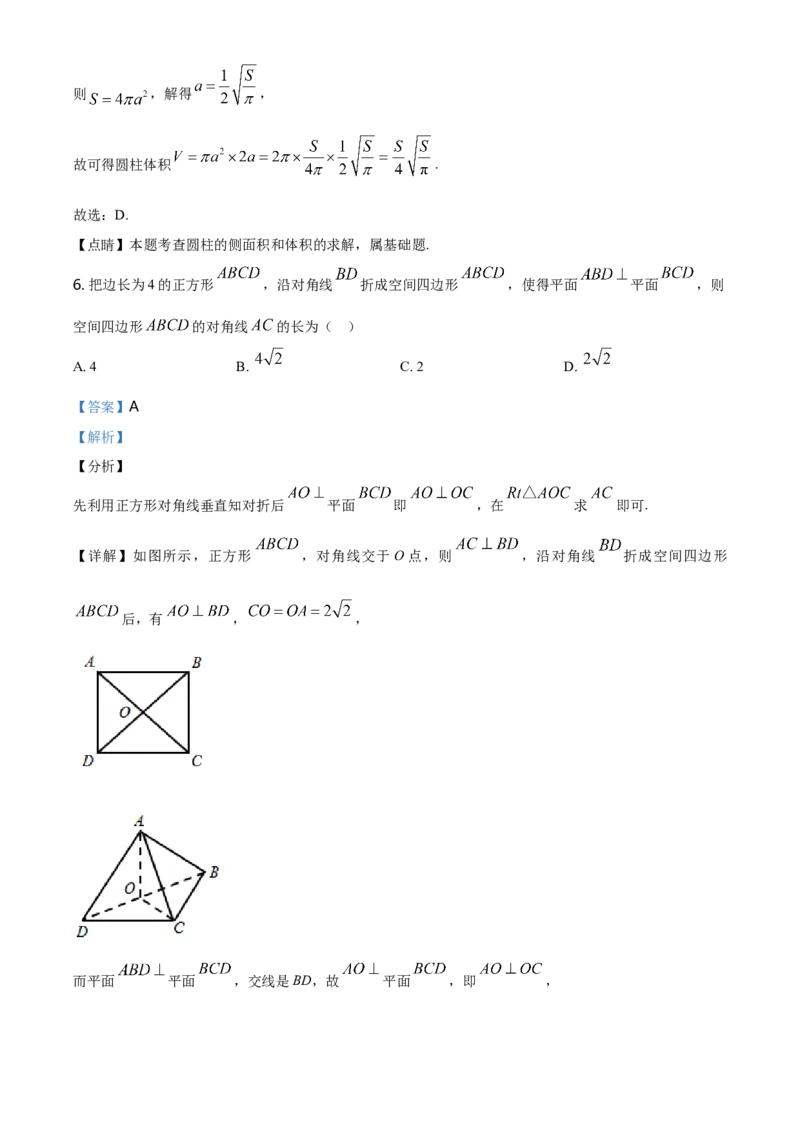
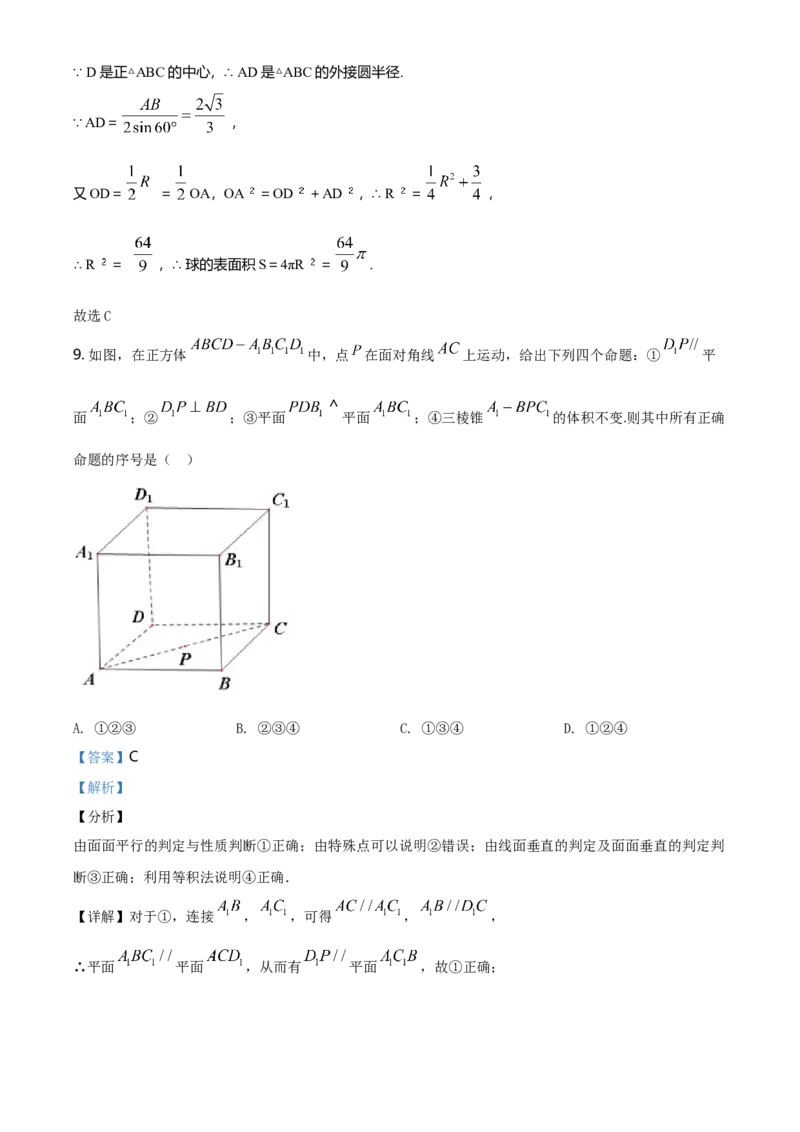
6. 把边长为4的正方形 ,沿对角线 折成空间四边形 ,使得平面 平面 ,则
空间四边形 的对角线 的长为( )
A. 4 B. C. 2 D.
【答案】A
【解析】
【分析】
先利用正方形对角线垂直知对折后 平面 即 ,在 求 即可.
【详解】如图所示,正方形 ,对角线交于O点,则 ,沿对角线 折成空间四边形
后,有 , ,
而平面 平面 ,交线是BD,故 平面 ,即 ,所以 是等腰直角三角形,故 .
故选:A.
【点睛】本题考查了面面垂直的性质定理,属于基础题.
7. 在 中, , , ,则 的面积是( )
A. B. C. D.
【答案】C
【解析】
【分析】
利用已知条件先求出 ,在 中,利用正弦定理求出 ,再利用三角形面积公式求解即可.
【详解】由 , ,
得 ,
在 中,
由正弦定理得:
,
则 的面积是:
,
所以 的面积是 .
故选:C.
【点睛】本题主要考查了正弦定理以及三角形面积公式,考查了两角和的正弦公式.属于较易题.
8. 已知过球面上 三点的截面和球心的距离等于球半径的一半,且 ,则球面积
是( )
A. B. C. D.
【答案】C
【解析】∵ D是正△ABC的中心,∴ AD是△ABC的外接圆半径.
∵ AD= ,
又OD= = OA,OA =OD +AD ,∴ R = ,
∴ R = ,∴ 球的表面积S=4πR = .
故选C
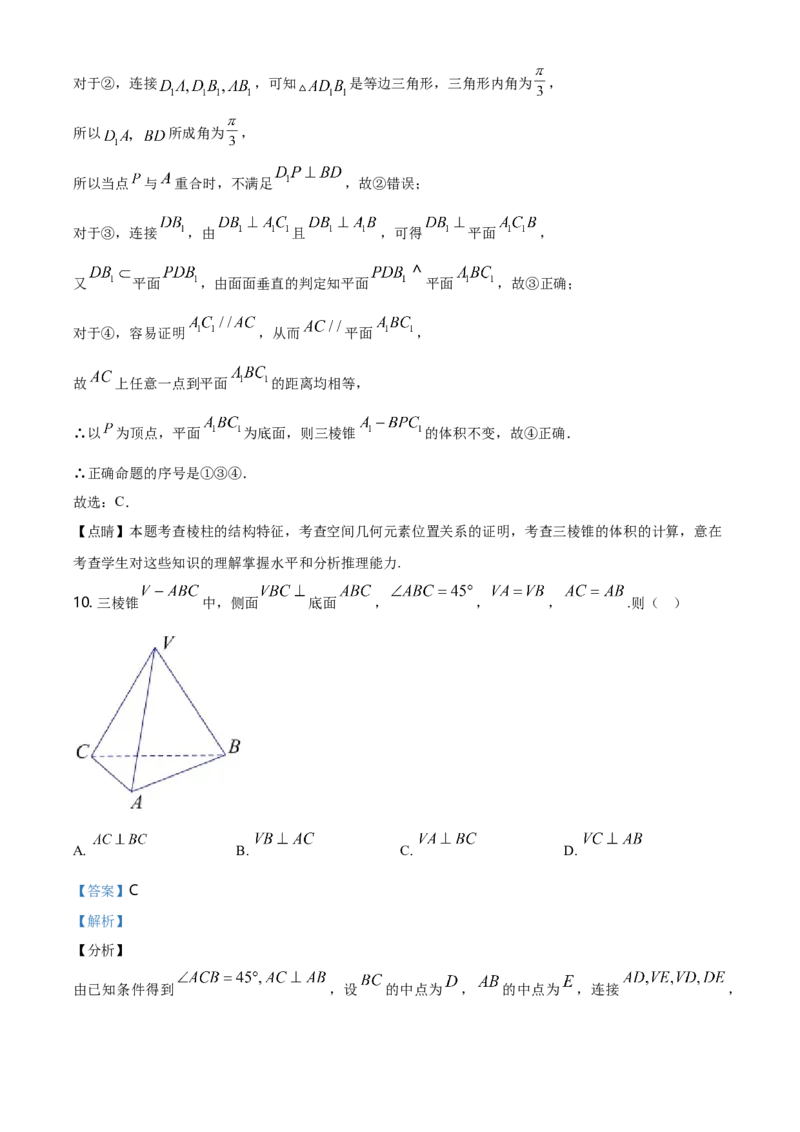
9. 如图,在正方体 中,点 在面对角线 上运动,给出下列四个命题:① 平
面 ;② ;③平面 平面 ;④三棱锥 的体积不变.则其中所有正确
命题的序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
【答案】C
【解析】
【分析】
由面面平行的判定与性质判断①正确;由特殊点可以说明②错误;由线面垂直的判定及面面垂直的判定判
断③正确;利用等积法说明④正确.
【详解】对于①,连接 , ,可得 , ,
∴平面 平面 ,从而有 平面 ,故①正确;对于②,连接 ,可知 是等边三角形,三角形内角为 ,
所以 所成角为 ,
所以当点 与 重合时,不满足 ,故②错误;
对于③,连接 ,由 且 ,可得 平面 ,
又 平面 ,由面面垂直的判定知平面 平面 ,故③正确;
对于④,容易证明 ,从而 平面 ,
故 上任意一点到平面 的距离均相等,
∴以 为顶点,平面 为底面,则三棱锥 的体积不变,故④正确.
∴正确命题的序号是①③④.
故选:C.
【点睛】本题考查棱柱的结构特征,考查空间几何元素位置关系的证明,考查三棱锥的体积的计算,意在
考查学生对这些知识的理解掌握水平和分析推理能力.
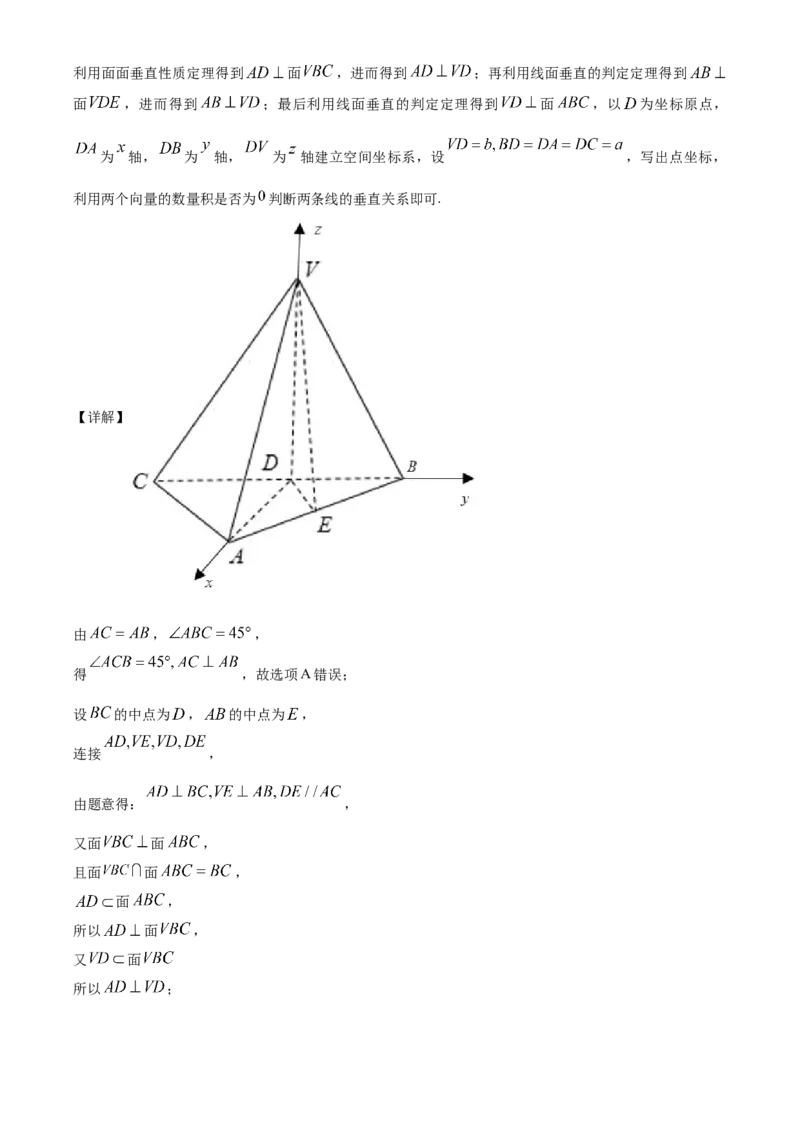
10. 三棱锥 中,侧面 底面 , , , .则( )
A. B. C. D.
【答案】C
【解析】
【分析】
由已知条件得到 ,设 的中点为 , 的中点为 ,连接 ,利用面面垂直性质定理得到 面 ,进而得到 ;再利用线面垂直的判定定理得到
面 ,进而得到 ;最后利用线面垂直的判定定理得到 面 ,以 为坐标原点,
为 轴, 为 轴, 为 轴建立空间坐标系,设 ,写出点坐标,
利用两个向量的数量积是否为 判断两条线的垂直关系即可.
【详解】
由 , ,
得 ,故选项A错误;
设 的中点为 , 的中点为 ,
连接 ,
由题意得: ,
又面 面 ,
且面 面 ,
面 ,
所以 面 ,
又 面
所以 ;,
所以 ,
又 , ,
面 ,
则 面 ,
所以 ;
又 ,
面 ,
所以 面 ,
则 ,
所以以 为坐标原点, 为 轴, 为 轴, 为 轴建立空间坐标系,
设 ,
则 ,
所以 ,
,
所以 ,
故 ,选项BD错误,选项C正确.
故选:C.
【点睛】本题主要考查了线面垂直的判定定理以及面面垂直的性质定理,考查了利用空间向量求解两条直
线的垂直问题.属于中档题.
二、填空题:本大题共5小题,每小题4分,共20分,把答案填在答题纸中相应位置上.
11. 在 中,角 , , 的对边分别为 , , .若 ,则角 的大小为
________.
【答案】
【解析】【分析】
利用余弦定理结合已知条件求 的余弦值即得结果.
【详解】因为 ,所以 ,
又 中, ,故 ,
故答案为: .
【点睛】本题考查了利用余弦定理求角,属于基础题 .
12. 在 中,若 , , ,则 等于________.
【答案】 或 .
【解析】
【分析】
由正弦定理,求得 ,得到 或 ,分类讨论,即可求得 的值.
【详解】由正弦定理,可得 ,所以 ,
因为 ,所以 或 ,
当 时, ,可得 ;
当 时, ,此时 ,
综上可得 或 .
故答案为: 或 .
【点睛】本题主要考查了正弦定理的应用,其中解答中利用正弦定理求得 的值,得出 的大小是解
答的关键,着重考查分类讨论,以及运算与求解能力.
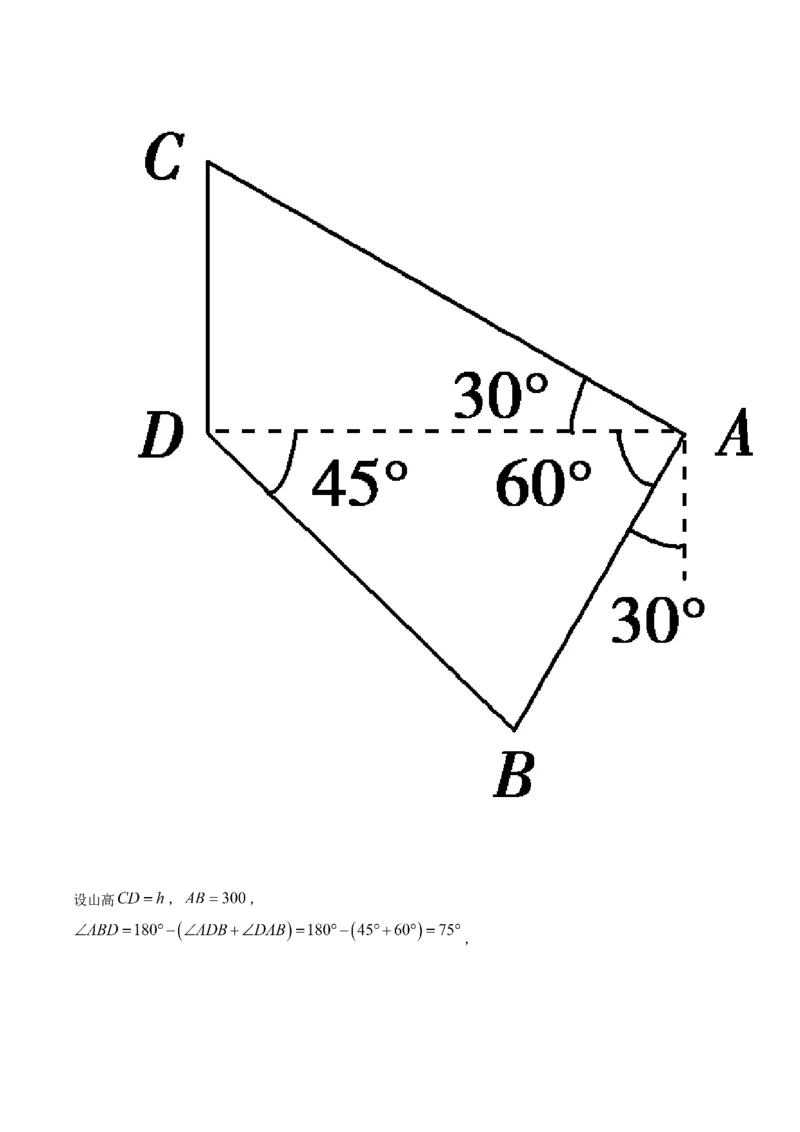
13. 在平地上有 、 两点, 在山的正东, 在山的东南,且 在 的南偏西 距离 点300米的地
方,在 测得山顶的仰角是 ,则山高为________米.【答案】
【解析】
【分析】
先设山高 ,依题意可得 ,由正弦定理可求得 ,在直角 中, 计
算得出结果即可.
【 详 解 】设山高 , ,
,由正弦定理得 .
在直角 中,
(米).
故山高为 米.
故答案为: .
【点睛】本题主要考查正弦定理在解三角形中的应用,属于较易题.
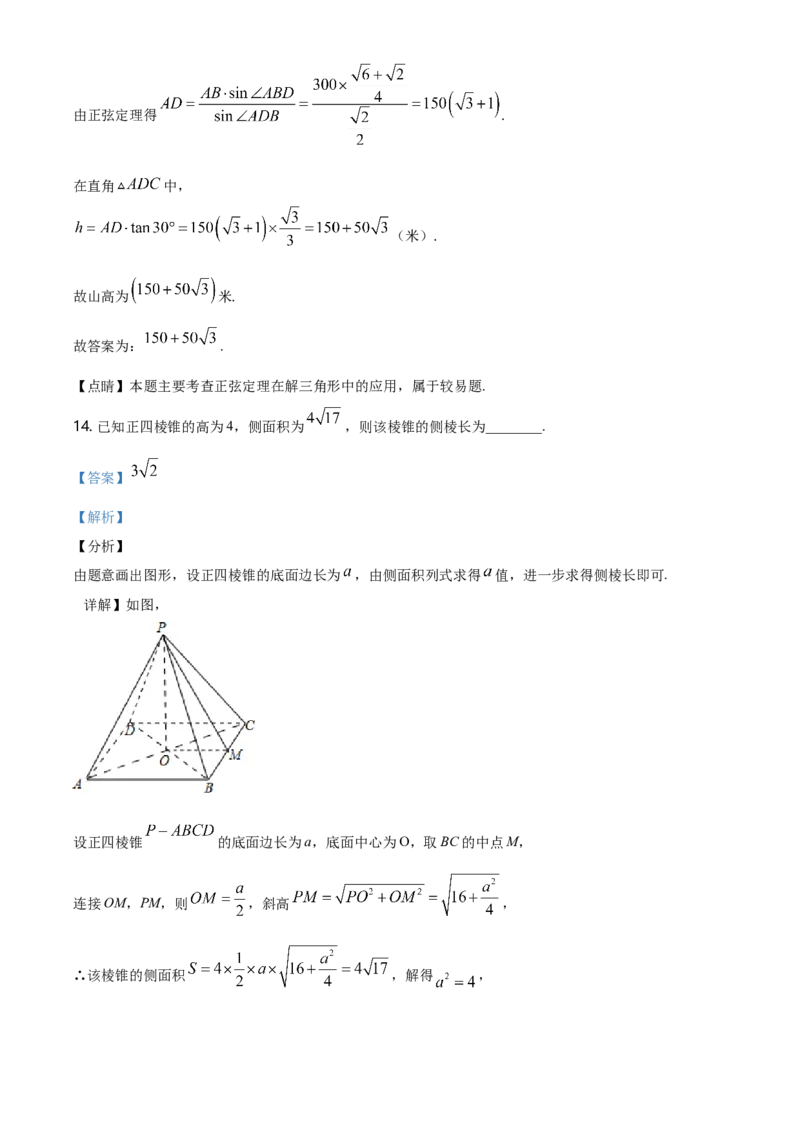
14. 已知正四棱锥的高为4,侧面积为 ,则该棱锥的侧棱长为________.
【答案】
【解析】
【分析】
由题意画出图形,设正四棱锥的底面边长为 ,由侧面积列式求得 值,进一步求得侧棱长即可.
【详解】如图,
设正四棱锥 的底面边长为a,底面中心为O,取BC的中点M,
连接OM,PM,则 ,斜高 ,
∴该棱锥的侧面积 ,解得 ,又 ,
∴该棱锥的侧棱长为 ,
故答案 为: .
【点睛】本题考查棱柱的结构特征,考查正四棱锥侧面积的求法,属于基础题.
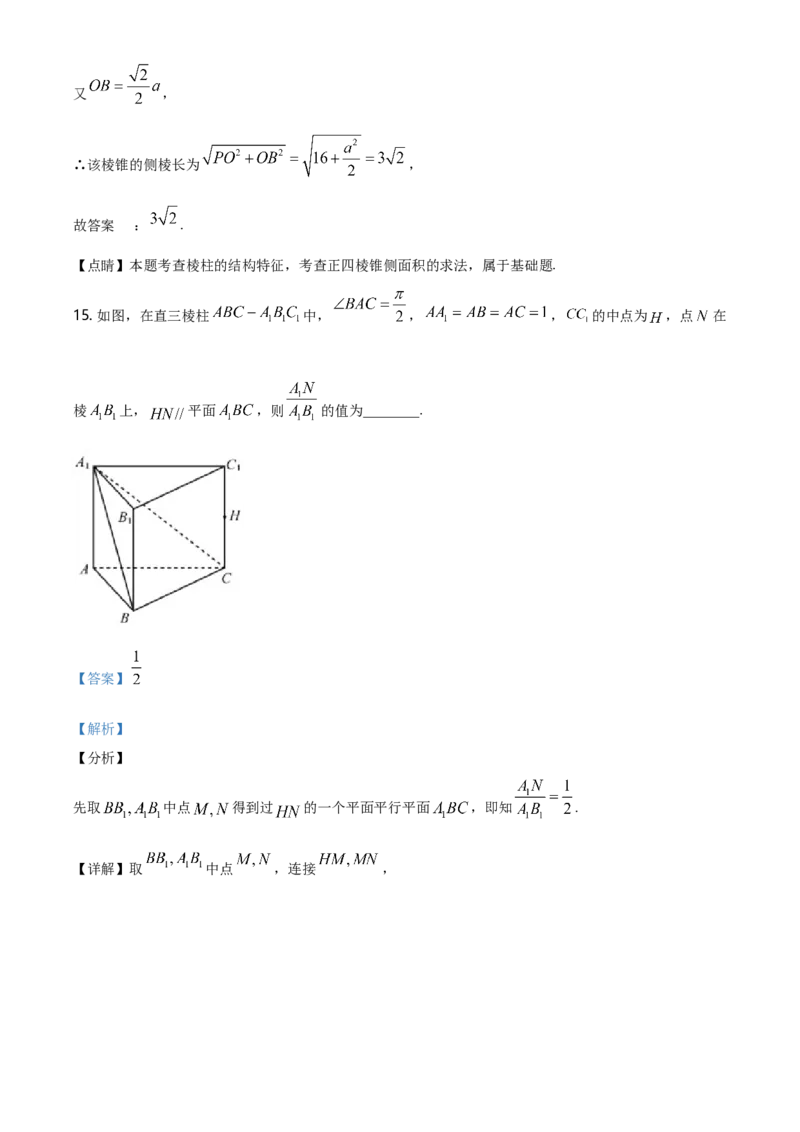
15. 如图,在直三棱柱 中, , , 的中点为 ,点 在
棱 上, 平面 ,则 的值为________.
【答案】
【解析】
【分析】
先取 中点 得到过 的一个平面平行平面 ,即知 .
【详解】取 中点 ,连接 ,故 , ,又 在平面 外, 平面
所以 平面 , 平面 ,又 相交在平面 内,故平面 平面
,即 平面 ,故 .
故答案为: .
【点睛】本题考查了面面平行的判定定理,属于基础题.
三、解答题:本大题共4小题,共40分.解答应写出文字说明,证明过程或演算步骤.
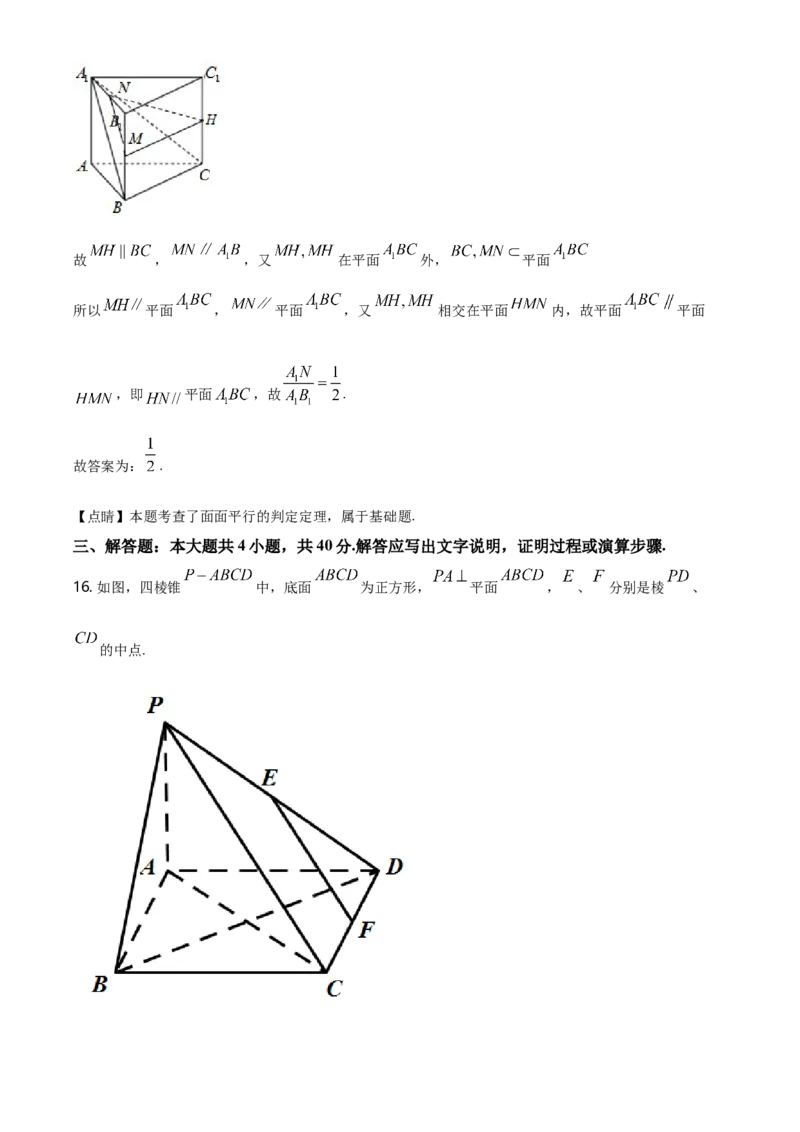
16. 如图,四棱锥 中,底面 为正方形, 平面 , 、 分别是棱 、
的中点.(1)求证: 平面 ;
(2)求证: .
【答案】(1)证明见详解;(2)证明见详解.
【解析】
【分析】
(1)由 、 分别是棱 、 的中点,可得: ,利用线面平行的判定定理证明即可;
(2)利用已知条件得到 , ,利用线面垂直的判定定理证明 面 ,所以
,又由(1)得 ,即可得证.
【详解】证明:(1)由 、 分别是棱 、 的中点,
可得: ,
又 平面 , 平面 ,
所以 平面 ;
(2)∵底面 为正方形,
,
又 平面 ,
所以 ,
又 ,
面 ,
所以 面 ,
所以 ,
又由(1)得 ,
所以 .
【点睛】本题主要考查了线面垂直、线面平行的判定定理,考查了推理能力与空间想象能力,属于较易题.
17. 在 中, , , 的面积为 .
(1)求 ;(2)求 的值.
【答案】(1) 或 ;(2) 或 .
【解析】
【分析】
(1)根据三角形的面积公式求得 的值,从而可以确定出角 的大小;
(2)由余弦定理求出 ,结合正弦定理可求出 的值.
【详解】(1)因为 , , 的面积为 ,
所以有 ,所以 ,
因为 ,所以 或 ;
(2)由余弦定理可得:
当 时, ,
所以 ,
由正弦定理, ,得 ,
当 时, ,
所以 ,
由正弦定理, ,得 ,所以 的值为 或 .
【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有三角形的面积公式,余弦定理解三角形,
正弦定理解三角形,属于简单题目.
18. 在 中,设内角 , , 所对的边分别为 , , , .
(1)求 ;
(2)若 , 边上的中线 长为 ,求边 .
【答案】(1) ;(2) .
【解析】
【分析】
(1)由题中条件,根据正弦定理,先得到 ,代入 ,即可得出结果;
(2)根据 为 边上的中线,得到 ,根据余弦定理,得出
,再由 得出 ,两式联立,即可得出结果.
【详解】(1)因为 ,
在 中,由正弦定理可得 ,
则 ,
所以 ,解得 (负值舍去);
(2)因为 为 边上的中线,所以 与 互补,
则 ,
因为 , , ,由余弦定理可得 ,
,
则 ,所以 ,
又在 中, ,
则 ,
因此 ,整理得 ,解得 或 (舍).
【点睛】本题主要考查解三角形,熟记正弦定理和余弦定理即可,属于常考题型.
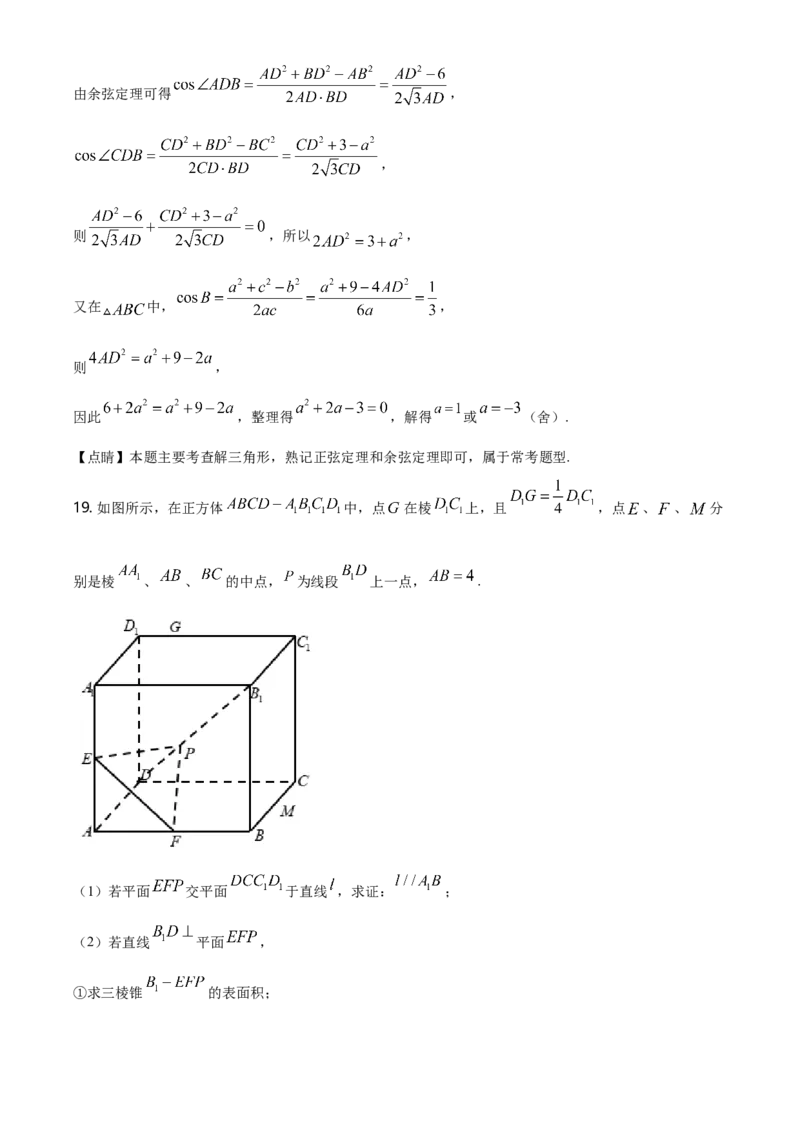
19. 如图所示,在正方体 中,点 在棱 上,且 ,点 、 、 分
别是棱 、 、 的中点, 为线段 上一点, .
(1)若平面 交平面 于直线 ,求证: ;
(2)若直线 平面 ,
①求三棱锥 的表面积;②试作出平面 与正方体 各个面的交线,并写出作图步骤,保留作图痕迹设平面
与棱 交于点 ,求三棱锥 的体积.
【答案】(1)答案见详解;(2)① ;②作图步骤见解析,三棱锥 的体积为 .
【解析】
【分析】
(1)根据面面平行的性质即可得到 ,再结合线线平行的传递性即可证明结论;
(2)①先根据直线 平面 得到 ,进而得到 是 的中点,然后依次求出三棱锥的
四个面的面积再相加即可得到三棱锥 的表面积;②根据公理“一条直线上的两点在一个平面内,
那么这条直线在此平面内”作出平面 与正方体 各个面的交线即可;根据 四
点共面,且三角形 与三角形 面积相等,那么三棱锥 的体积等于三棱锥 的体
积,直接利用三棱锥的体积公式求解即可.
【详解】(1)在正方体 中,
因为平面 平面 ,平面 平面 ,
所以 ,
因为点 、 分别是棱 、 的中点,
所以 ,
所以 .
(2)①因为直线 平面 , 平面 ,
所以 ,又因为 △ ,所以 ,
所以 ,
因为 ,
,
,
所以三棱锥 的表面积为 .
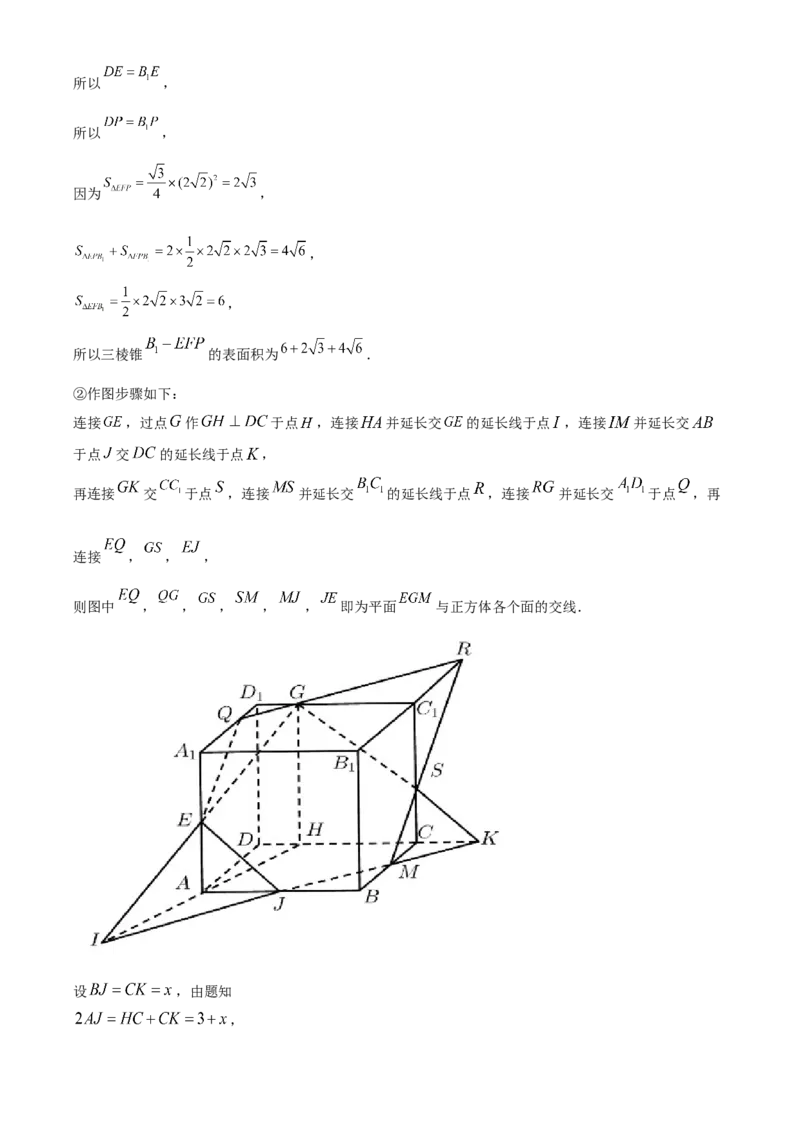
②作图步骤如下:
连接 ,过点 作 于点 ,连接 并延长交 的延长线于点 ,连接 并延长交
于点 交 的延长线于点 ,
再连接 交 于点 ,连接 并延长交 的延长线于点 ,连接 并延长交 于点 ,再
连接 , , ,
则图中 , , , , , 即为平面 与正方体各个面的交线.
设 ,由题知
,所以 ,所以 ,
解得 ,
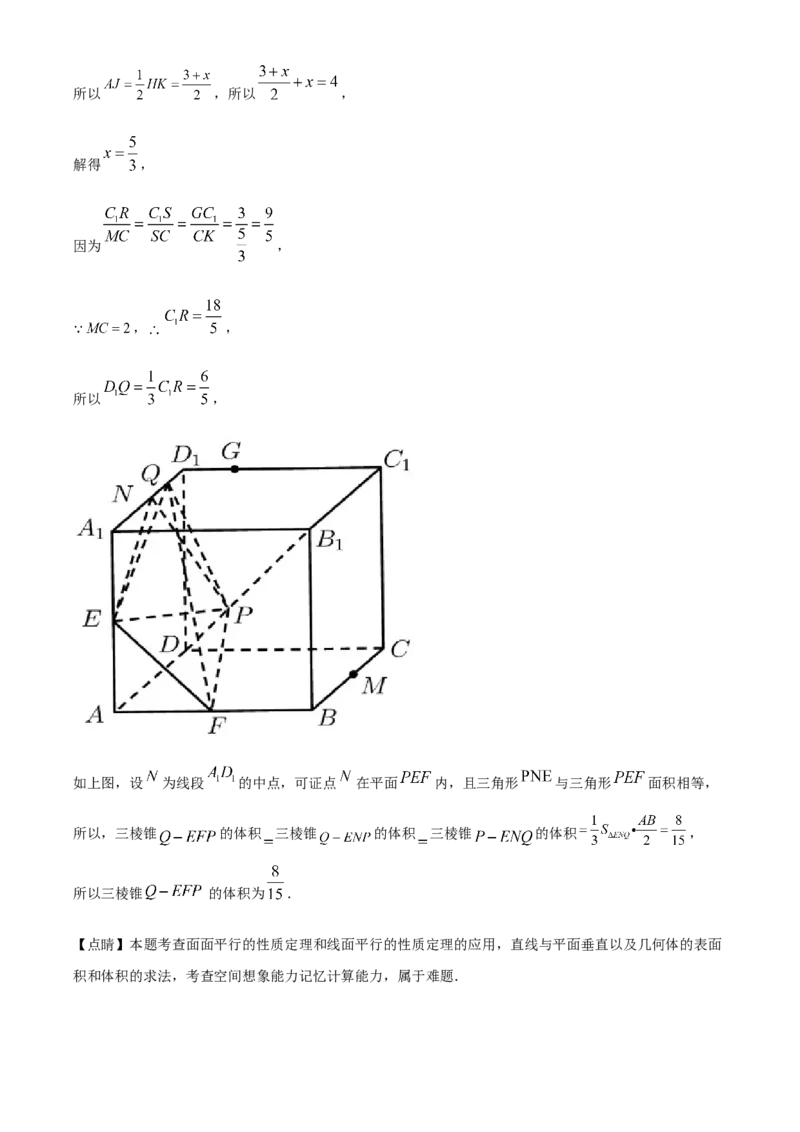
因为 ,
, ,
所以 ,
如上图,设 为线段 的中点,可证点 在平面 内,且三角形 与三角形 面积相等,
所以,三棱锥 的体积 三棱锥 的体积 三棱锥 的体积 ,
所以三棱锥 的体积为 .
【点睛】本题考查面面平行的性质定理和线面平行的性质定理的应用,直线与平面垂直以及几何体的表面
积和体积的求法,考查空间想象能力记忆计算能力,属于难题.