文档内容
第二学期七校联考
高一数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.
1. 已知复数 ,则 的虚部为( )
A. B. 1 C. D.
【答案】C
【解析】
【分析】先化简求出 ,即可得出答案.
【详解】因为 ,所以 的虚部为 .
故选:C.
2. 在 中,若 , , ,则 的值为( )
A. B. C. D.
【答案】D
【解析】
【分析】由面积公式直接进行求解.
【详解】
故选:D
3. 已知一组数据为85,87,88,90,92,则这组数据的第60百分位数为( )
A. 87 B. 87.5 C. 89 D. 91
【答案】C
【解析】
【分析】根据一组数的百分位数的定义直接计算即可.
【详解】该组数据从小到大排序为85,87,88,90,92,共5个数据,而 ,
学科网(北京)股份有限公司所以这组数据的第60百分位数为 .
故选:C.
4. 一个正四棱锥的底面边长为 ,高为 ,则该正四棱锥的表面积为( )
A. B. C. D.
【答案】B
【解析】
的
【分析】计算出正四棱锥 侧棱长以及侧面三角形的高,进而可计算出该正四棱锥的表面积.
【详解】如下图所示,在正四棱锥 中,底面 的边长为 ,
设点 在底面 的射影点为点 ,则四棱锥 的高 ,
则 为 的中点,且 , ,
取 的中点 ,连接 ,则 ,且 ,
,故正四棱锥 的表面积为 .
故选:B.
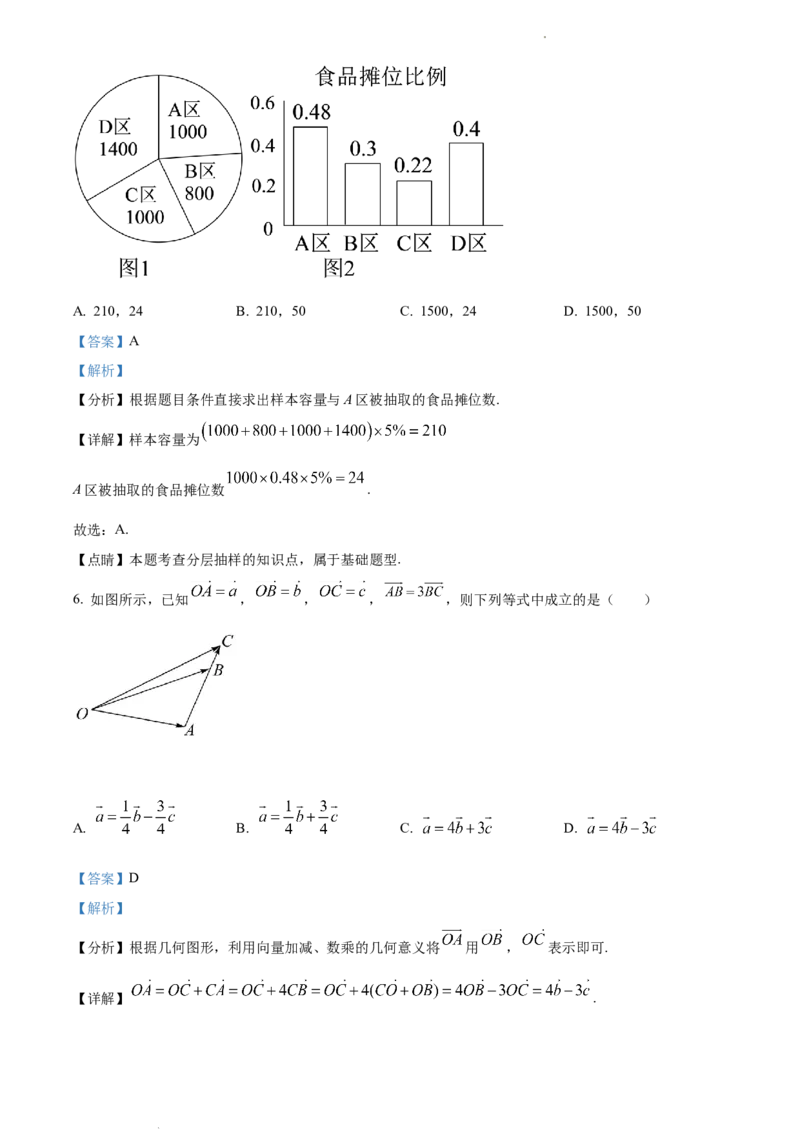
5. 今年6月初,某市采取了鼓励地摊经济的做法,该市各区的地摊的摊位数和食品摊位比例分别如图1、
图2所示,现用分层抽样的方法抽取 的摊位进行调查,则抽取的样本容量与A区被抽取的食品摊位数
分别为( )
学科网(北京)股份有限公司A. 210,24 B. 210,50 C. 1500,24 D. 1500,50
【答案】A
【解析】
【分析】根据题目条件直接求出样本容量与A区被抽取的食品摊位数.
【详解】样本容量为
A区被抽取的食品摊位数 .
故选:A.
【点睛】本题考查分层抽样的知识点,属于基础题型.
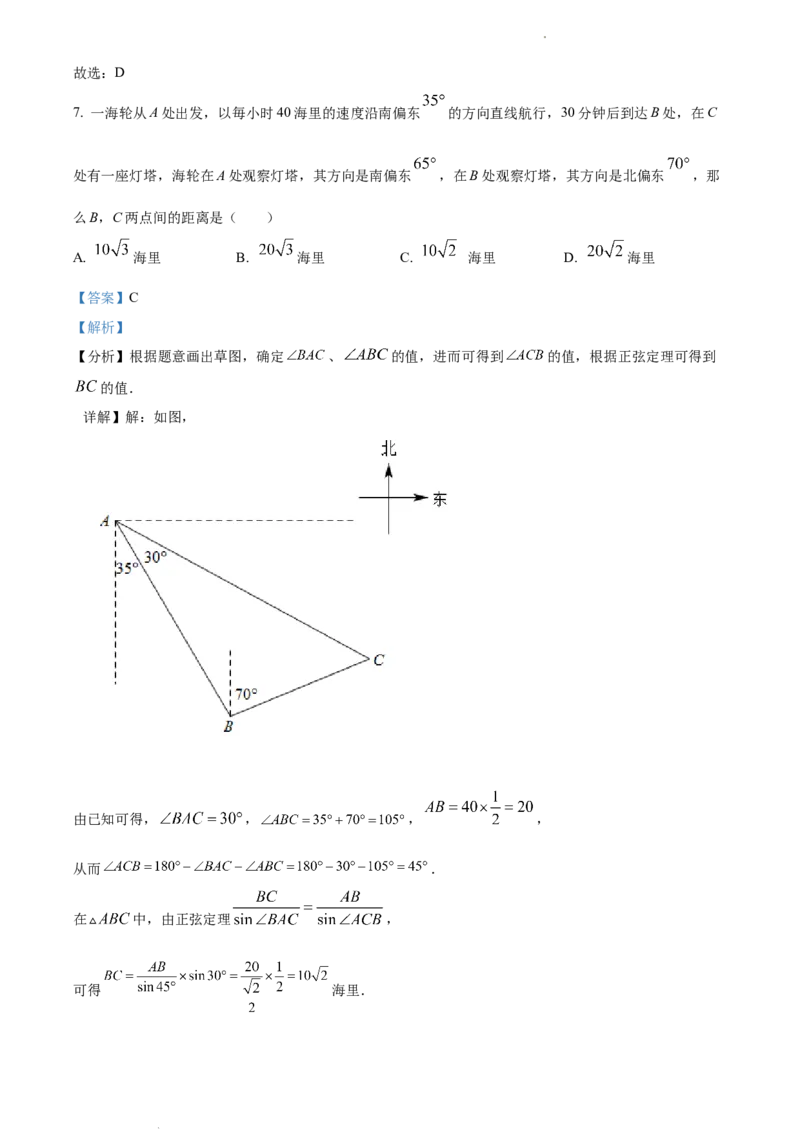
6. 如图所示,已知 , , , ,则下列等式中成立的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据几何图形,利用向量加减、数乘的几何意义将 用 , 表示即可.
【详解】 .
学科网(北京)股份有限公司故选:D
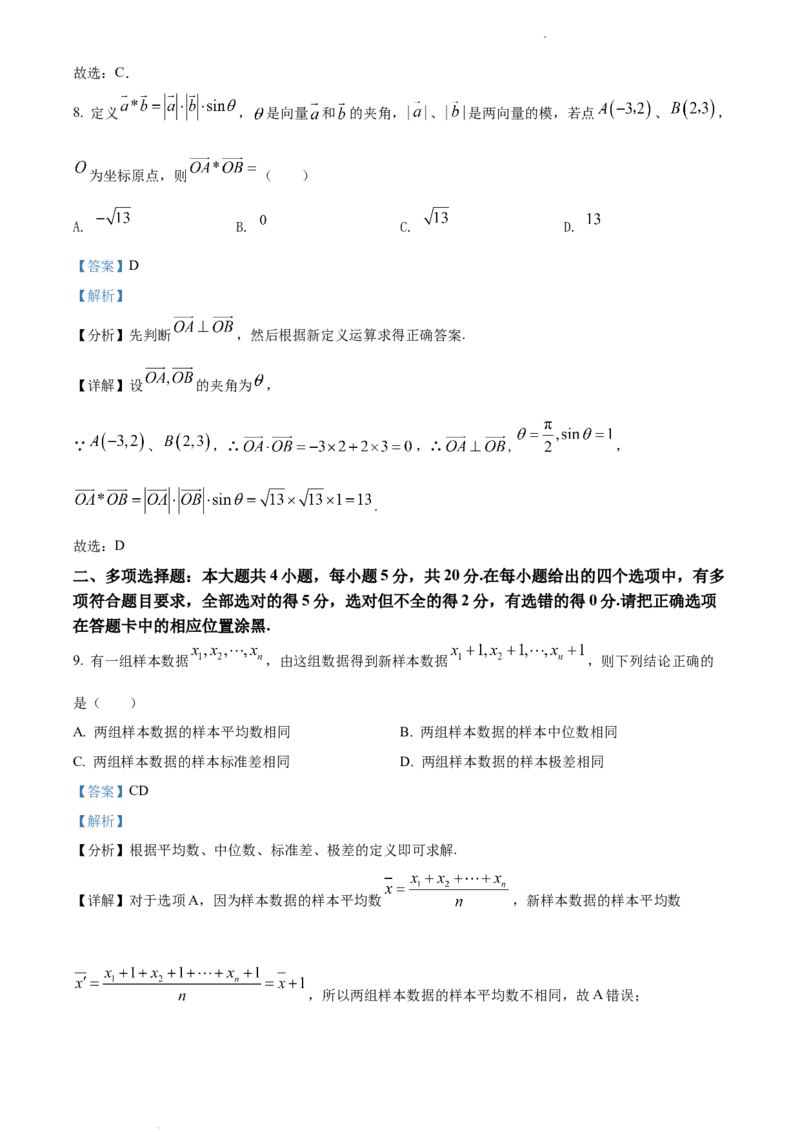
7. 一海轮从A处出发,以毎小时40海里的速度沿南偏东 的方向直线航行,30分钟后到达B处,在C
处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东 ,在B处观察灯塔,其方向是北偏东 ,那
么B,C两点间的距离是( )
A. 海里 B. 海里 C. 海里 D. 海里
【答案】C
【解析】
【分析】根据题意画出草图,确定 、 的值,进而可得到 的值,根据正弦定理可得到
的值.
【详解】解:如图,
由已知可得, , , ,
从而 .
在 中,由正弦定理 ,
可得 海里.
学科网(北京)股份有限公司故选:C.
8. 定义 , 是向量 和 的夹角, 、 是两向量的模,若点 、 ,
为坐标原点,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】先判断 ,然后根据新定义运算求得正确答案.
【详解】设 的夹角为 ,
∵ 、 ,∴ ,∴ , ,
.
故选:D
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多
项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.请把正确选项
在答题卡中的相应位置涂黑.
9. 有一组样本数据 ,由这组数据得到新样本数据 ,则下列结论正确的
是( )
A. 两组样本数据的样本平均数相同 B. 两组样本数据的样本中位数相同
C. 两组样本数据的样本标准差相同 D. 两组样本数据的样本极差相同
【答案】CD
【解析】
【分析】根据平均数、中位数、标准差、极差的定义即可求解.
【详解】对于选项A,因为样本数据的样本平均数 ,新样本数据的样本平均数
,所以两组样本数据的样本平均数不相同,故A错误;
学科网(北京)股份有限公司对于选项B,设样本数据 的中位数为 ,则新样本数据 的中位数为
,所以两组样本数据的样本中位数不相同,故B错误;
对于选项C,样本数据的标准差为
新样本数据的样本标准差为
,故C正确;
对于选项D,设样本数据 中, 最大, 最小,所以样本数据的极差 ,新样本数据
中, 最大, 最小,新样本数据的极差 ,故D正
确.
.
故选:CD
10. 已知复数 则( )
A. 是纯虚数 B. 对应的点位于第二象限
C. D.
【答案】AD
【解析】
【分析】利用复数的概念及几何有意义判断A、B选项是否正确,利用利用复数的四则运算法则计算
及 ,并计算出模长,判断C、D是否正确.
【详解】利用复数的相关概念可判断A正确;
对于B选项, 对应的点位于第四象限,故B错;
对于C选项, ,则 ,故C错;
对于D选项, ,则 ,故D正确.
学科网(北京)股份有限公司故选:AD
【点睛】本题考查复数的相关概念及复数的计算,较简单.
11. 在 中,角A,B,C所对的边分别为a,b,c,则正确的结论有( )
A. 若 ,则
B. 若 ,则 则为直角三角形
C. 若 为锐角三角形,则
D. 若 ,则 一定是等腰三角形
【答案】ABC
【解析】
【分析】A选项,由大角对大边和正弦定理进行推导;B选项,由正弦定理和勾股定理逆定理进行解答;
C选项,根据锐角三角形得到 ,结合正弦定理的单调性得到 ,利用诱导公
式进行解答;D选项,得到 或 ,所以是直角三角形或等腰三角形.
【详解】因为 ,所以 ,由正弦定理得: ,
所以 ,A正确;
若 ,由正弦定理得: ,
由勾股定理逆定理得: 则为直角三角形,B正确;
若 为锐角三角形,则 ,所以 ,且
由于 在 上单调递增,
学科网(北京)股份有限公司所以 ,即 ,C正确;
若 ,则 或 ,
所以 或 ,则 是等腰三角形或直角三角形,D正确.
故选:ABC
12. 在给出的下列命题中,正确的是( )
A. 设 是同一平面上的四个点,若 ,则点 必共
线
B. 若向量 是平面 上的两个向量,则平面 上的任一向量 都可以表示为 ,
且表示方法是唯一的
C. 已知平面向量 满足 则 为等腰三角形
D. 已知平面向量 满足 ,且 ,则 是等边三
角形
【答案】ACD
【解析】
【分析】
对于A,根据共线定理判断A、B、C三点共线即可;对于B,根据平面向量的基本定理,判断命题错误;
对于C,根据向量的运算性质可得OA为BC的垂线且OA在 的角平分线上,从而可判断C;对于
D,根据平面向量的线性表示与数量积运算得出命题正确;
【详解】对于A, ,
∴ ,∴ ,且有公共点C,
∴则点A、B、C共线,命题A正确;
对于B,根据平面向量的基本定理缺少条件 不共线,故B错误;
学科网(北京)股份有限公司对于C,由于 ,即 , ,
得 ,即OA为BC的垂线,
又由于 ,可得OA在 的角平分线上,
综合得 为等腰三角形,故C正确;
对于D,平面向量 、 、 满足 ,且 ,
∴ ,∴ ,
即 ,∴ ,
∴ 、 的夹角为 ,同理 、 的夹角也为 ,
∴ 是等边三角形,故D正确;
故选ACD.
【点睛】本题主要考查利用命题真假的判断考查了平面向量的综合应用问题,属于中档题.
三、填空题:本大题共4小题,每小题5分,共20分.其中第16题第一空2分,第二空3分.
请把答案填在答题卡的相应位置上.
13. 已知向量 , 满足: , , 与 的夹角为 ,则 ______.
【答案】
【解析】
【分析】根据向量的数量积公式及向量的摸公式即可求解.
【详解】因为 , , 与 的夹角为 ,
所以 ,
学科网(北京)股份有限公司所以 .
故答案为: .
14. 设 ,复平面内 对应的点为 .如果 满足下列条件: ,则点 的集合对应图形面积
是:________.(计算结果保留 )
【答案】
【解析】
【分析】利用复数的几何意义可得所求图形为圆环面,进而可得.
【详解】设 ,其中 , ,
由 可得 ,
∴ ,
∴复数 对应的点 的集合是以 为圆心, , 为半径的圆所夹的圆环面,
∴圆环面积为 .
故答案为: .
15. 已知一场足球比赛中,队员甲进球的概率为0.4,队员乙进球的概率为0.3,这两名队员是否进球相互
独立,则同一场比赛中他们两人至少有一人进球的概率为____________.
【答案】0.58
【解析】
【分析】利用独立事件与对立事件的概率公式求解即可.
【详解】解:一场足球比赛中,队员甲进球的概率为0.4,队员乙进球的概率为0.3,这两名队员是否进球
相互独立,
同一场比赛中他们两人至少有一人进球的对立事件是他们两人同时不进球,
∴同一场比赛中他们两人至少有一人进球的概率为: .
故答案为:0.58.
16. 在 中,角A,B,C所对的边分别为a,b,c,若 ,则 ________,
学科网(北京)股份有限公司________.
【答案】 ①. ②.
【解析】
【分析】
利用余弦定理求出 ,再根据正弦定理求出 、 即可求解.
【详解】在 中, ,
则 ,即 ,
解得 或 (舍去).
由正弦定理 ,
解得 , ,
所以 .
四、解答题:本大题共6小题,第17题10分,18、19、20、21、22题各,共70分.解答应写
出文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出
指定区域的答案无效.
17. 已知复数 , .
(1)若复数 在复平面上对应的点在第三象限,求实数 的取值范围.
(2)若 ,求 的共轭复数 .
【答案】(1) ;(2) .
【解析】
学科网(北京)股份有限公司【分析】(1)由题意求出 ,结合复数的几何意义和各象限的点的坐标特征即可.
(2)利用复数的除法运算法则求出z,进而求出z的共轭复数.
【详解】解:( )因为 , ,
所以 .
因为复数 在复平面上对应的点在第三象限,所以
解得 ,即实数 的取值范围为 .
( )因 为 ,
所以 .
18. 已知向量 .
(1)求向量 与 的夹角的大小;
(2)若 ,求实数 的值.
【答案】(1) ;(2)
【解析】
【分析】(1)由 ,计算可求出答案;
(2)先求出 ,再根据 ,可得 ,进而可列出方程,即可求出 的值.
【详解】(1)由题意, .
因为 ,故 .
学科网(北京)股份有限公司(2) ,
因为 ,所以 ,
即 ,解得 .
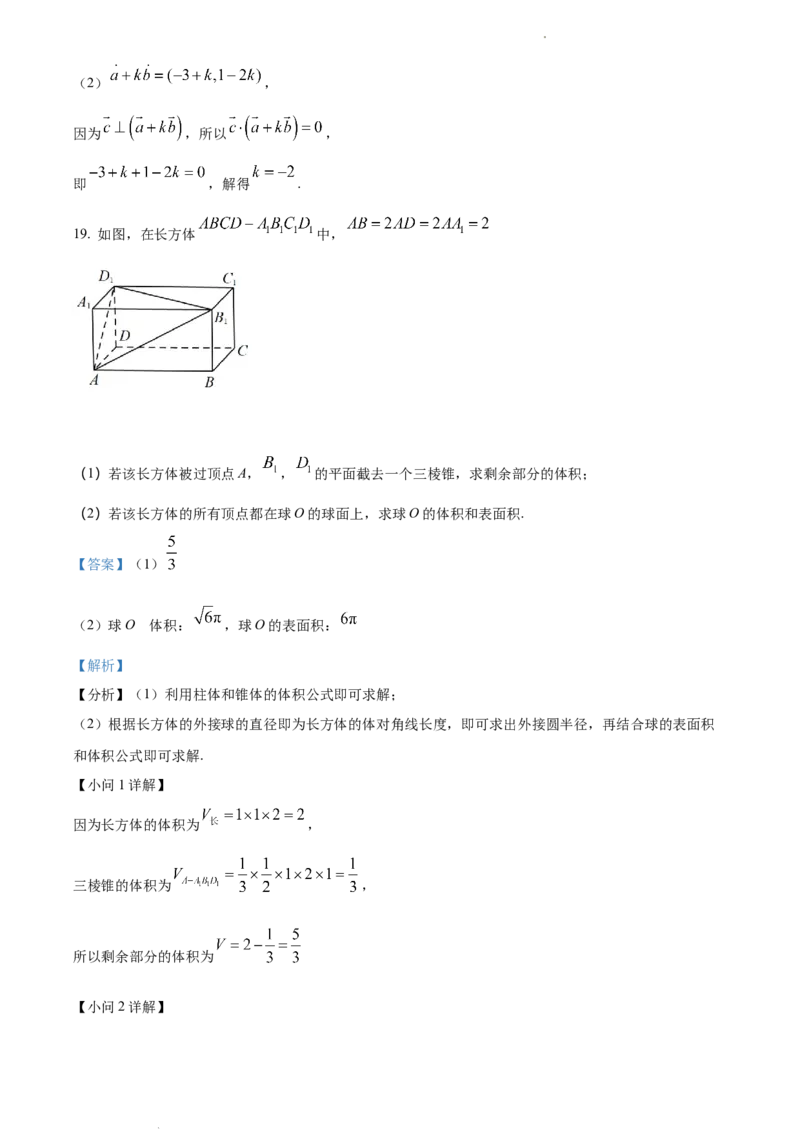
19. 如图,在长方体 中,
(1)若该长方体被过顶点A, , 的平面截去一个三棱锥,求剩余部分的体积;
(2)若该长方体的所有顶点都在球O的球面上,求球O的体积和表面积.
【答案】(1)
的
(2)球O 体积: ,球O的表面积:
【解析】
【分析】(1)利用柱体和锥体的体积公式即可求解;
(2)根据长方体的外接球的直径即为长方体的体对角线长度,即可求出外接圆半径,再结合球的表面积
和体积公式即可求解.
【小问1详解】
因为长方体的体积为 ,
三棱锥的体积为 ,
所以剩余部分的体积为
【小问2详解】
学科网(北京)股份有限公司由题可知球O为长方体的外接球,则球O的半径 ,
故球O的体积为 ,
球O的表面积: .
20. 在 中,角 所对的边分别为 ,且
(1)求角B;
(2)若 的面积为 ,BC边上的高 ,求 , 的值.
【答案】(1)
(2) ,
【解析】
【分析】(1)利用余弦定理角边互化,再利用三角函数的特殊值对应特殊角,结合角的范围即可求解;
(2)根据正弦定理及三角形的面积公式,再利用余弦定理即可求解.
【小问1详解】
因为 ,所以
所以 ,即
由余弦定理可得 ,
因为 ,所以
【小问2详解】
由(1)知, ,因为BC边上的高 ,所以 ,
在 中,由正弦定理可得 ,
学科网(北京)股份有限公司即 .
因为 的面积为 ,
所以 ,解得 .
在 中,由余弦定理,得
,则 .
所以 的值为 , 的值为 .
21. 东莞市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通
过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼,摄影协会收到了来自社会各界的大量
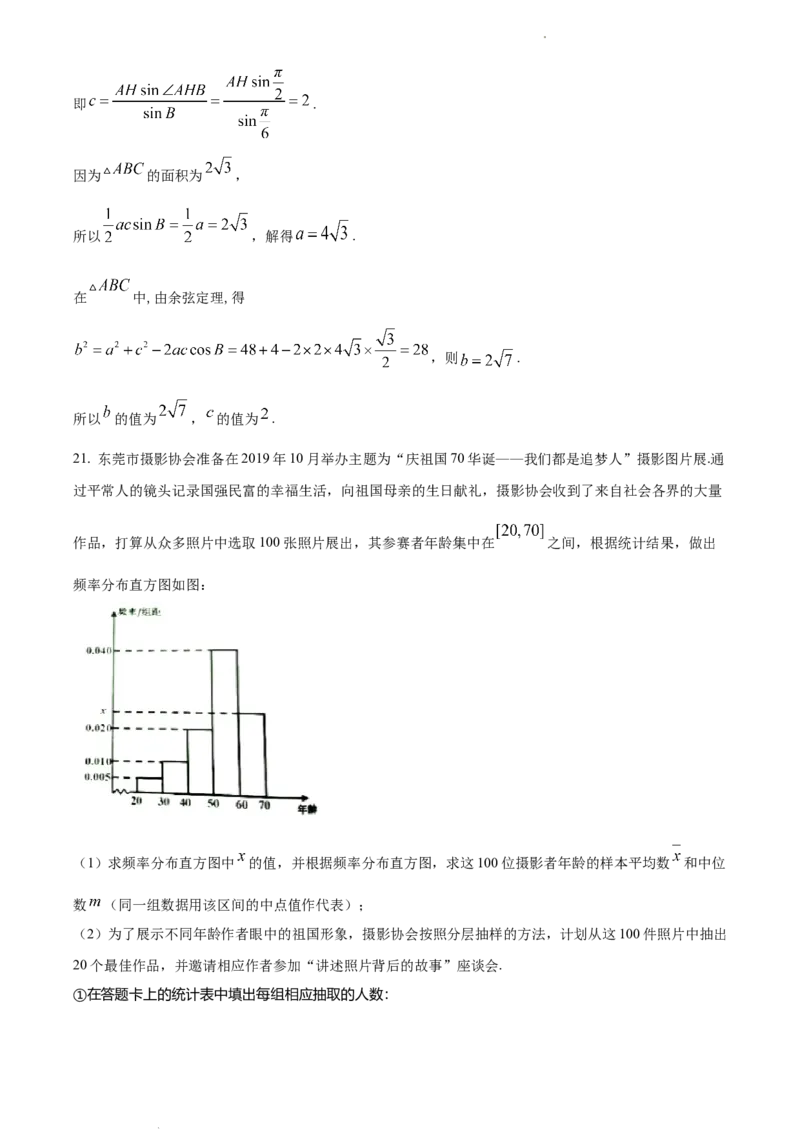
作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在 之间,根据统计结果,做出
频率分布直方图如图:
(1)求频率分布直方图中 的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数 和中位
数 (同一组数据用该区间的中点值作代表);
(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中抽出
20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
学科网(北京)股份有限公司年龄
人数
②若从年龄在 的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在
的概率.
【答案】(1) ,平均数 为 ,中位数为 (2)①见解析②
【解析】
【分析】(1)由频率分布直方图各个小矩形的面积之和为1可得 ,用区间中点值代替可计算均值,中位
数把频率分布直方图中小矩形面积等分.
(2)①分层抽样,是按比例抽取人数;②年龄在 有2人,在 有4人,设在 的是 ,
,在 的是 ,可用列举法列举出选2人的所有可能,然后可计算出概率.
【详解】(1)由频率分布直方图各个小矩形的面积之和为1,
得
在频率分布直方图中,这100位参赛者年龄的样本平均数为:
设中位数为 ,由 ,
解得 .
(2)①每组应各抽取人数如下表:
年龄
人数 1 2 4 8 5
②根据分层抽样的原理,年龄在 有2人,在 有4人,设在 的是 , ,在
的是 ,列举选出2人的所有可能如下:
学科网(北京)股份有限公司,
共15种情况.
设“这2人至少有一人的年龄在区间 ”为事件 ,则包含:
共9种情况
则
【点睛】本题考查频率分布直方图,考查样本数据特征、古典概型,属于基础题型.
22. 已知 的内角A,B,C所对的边分别为a,b,c,且
(1)若 , ,D为边BC上的中点,求 ;
(2)若E为边BC上一点,且 , ,求 的最小值.
【答案】(1)
(2)
【解析】
【分析】(1)由余弦定理和 求出 ,进而求出 ,进而求出
,平方后得到 ,从而求出 ;
(2)由 和 ,推导出 ,再利用基本不等式“1”的妙用求解出最小值.
【小问1详解】
依题意得: ,
学科网(北京)股份有限公司由 ,得:
∴
∵D为边BC的中点,∴
∴
即
【小问2详解】
∵E为边BC上一点, ,
∴ ,
即 ,
∴ ,
又 ,
∴ ,
∴ ,即 ,
∴ ,
当且仅当 ,即 取等号,
故 的最小值为 .
学科网(北京)股份有限公司