高二（上）期末模拟测试卷（A卷基础巩固）解析版_E015高中全科试卷_数学试题_选修1_04.期末试卷_高二（上）期末模拟测试卷（A卷基础巩固）

高二（上）期末模拟测试卷（A 卷 基础巩固） 考试时间：120分钟 满分：150分 一、单选题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题 目要求的．） 1．椭圆 的焦距为2，则 的值等于（ ）. A．5 B．8 C．5或3 D．5或8 【答案】C 【解析】当焦点在 轴上时： ， ，解得： ， 当焦点在 轴上时： ， ，解得： ， 所以 或 ，故选：C 2．椭圆 的焦点坐标是（ ） A． B． C． D． 【答案】．A 【详解】由题意，椭圆 ，即 ，可得椭圆的焦点在 轴上，且 ，所 以椭圆的焦点坐标为 故选： . A. 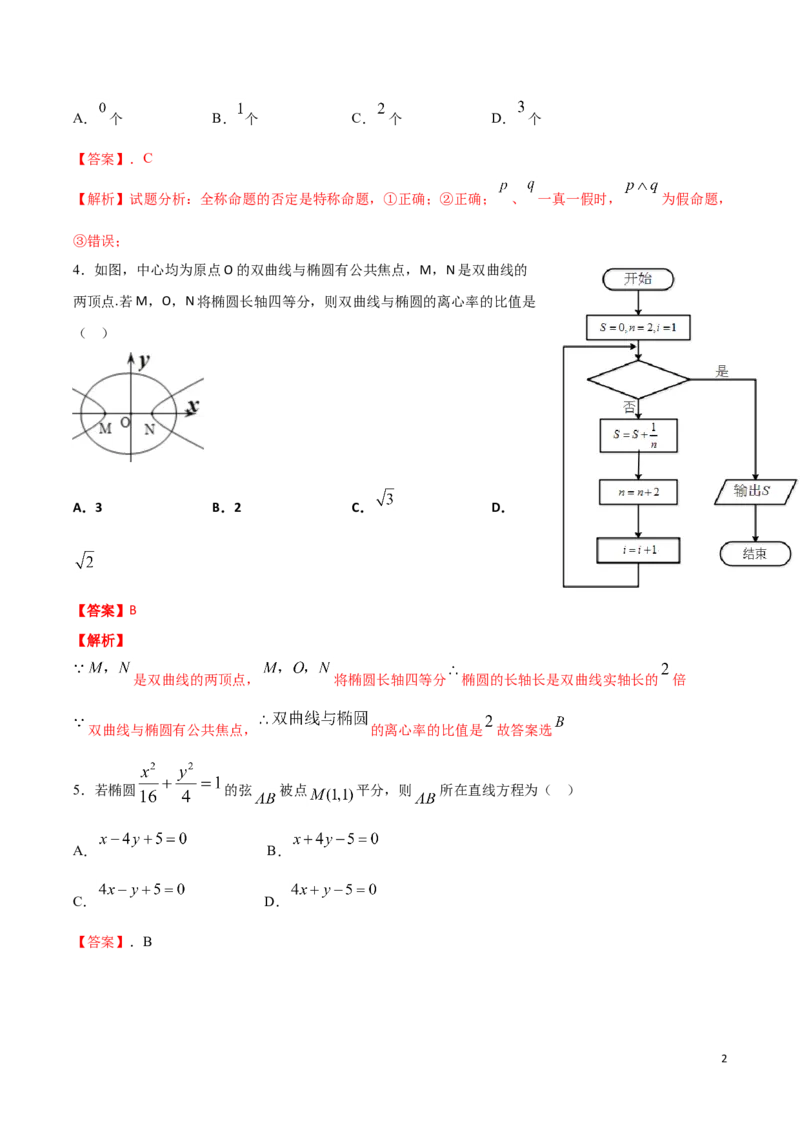3．以下命题正确的个数是（ ） ①命题“ ， ”的否定是“ ， ”． ②命题“若 ，则 ”的逆否命题为“若 ，则 ”． ③若 为假命题，则 、 均为假命题． 1A． 个 B． 个 C． 个 D． 个 【答案】．C 【解析】试题分析：全称命题的否定是特称命题，①正确；②正确； 、 一真一假时， 为假命题， ③错误； 4．如图，中心均为原点O的双曲线与椭圆有公共焦点，M，N是双曲线的 两顶点.若M，O，N将椭圆长轴四等分，则双曲线与椭圆的离心率的比值是 （ ） A．3 B．2 C． D． 【答案】B 【解析】 是双曲线的两顶点， 将椭圆长轴四等分 椭圆的长轴长是双曲线实轴长的 倍 双曲线与椭圆有公共焦点， 的离心率的比值是 故答案选 5．若椭圆 的弦 被点 平分，则 所在直线方程为（ ） A． B． C． D． 【答案】．B 2【详解】设 ，则满足 ，两式作差得 ， 又 被点 平分，故 ， 且直线 的斜率存在，所以 ， 化简得 ，则 所在直线方程为 ，化简得 故选：B ． 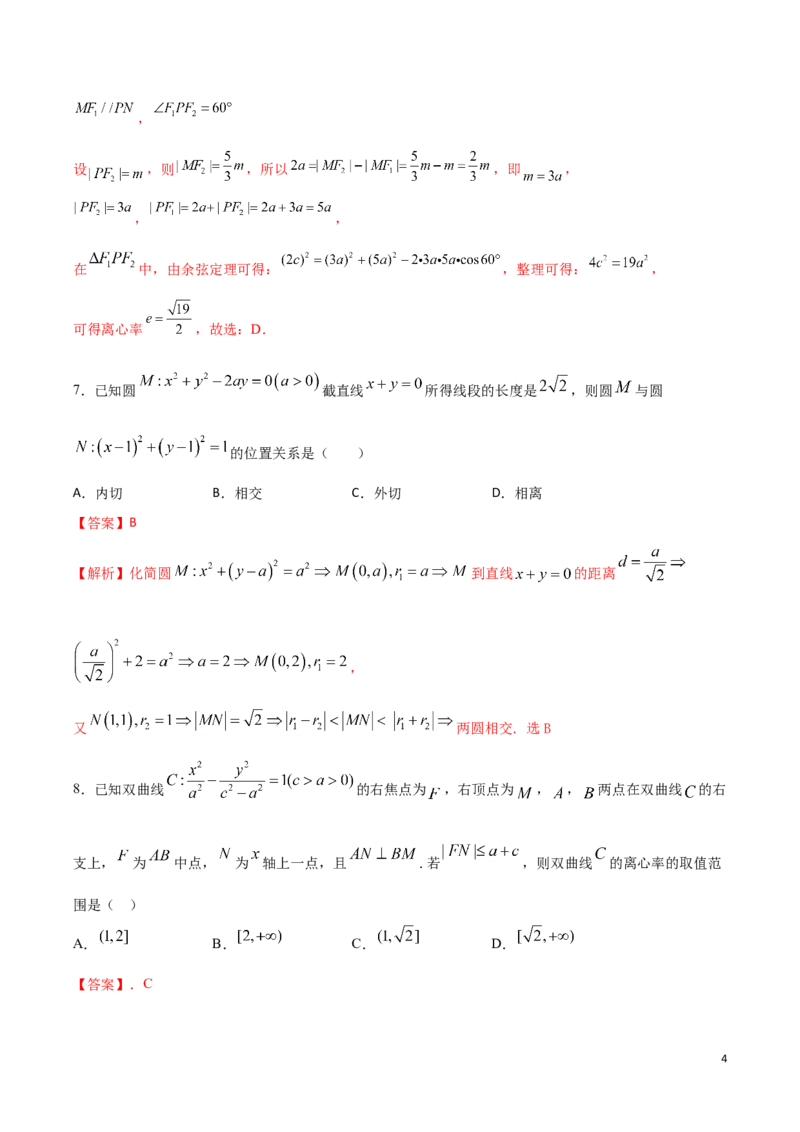6．设 是双曲线 的右焦点，O为坐标原点，过 的直线交双曲线的右支于点 P，N，直线PO交双曲线 于另一点M，若 ，且 ，则双曲线 的离心率为 （ ） A． B． C． D． 【答案】．D 【详解】解：设双曲线的左焦点 ，由双曲线的对称性可得 为平行四边形，所以 ， 3， 设 ，则 ，所以 ，即 ， ， ， 在 中，由余弦定理可得： ，整理可得： ， 可得离心率 ，故选：D． 7．已知圆 截直线 所得线段的长度是 ，则圆 与圆 的位置关系是（ ） A．内切 B．相交 C．外切 D．相离 【答案】B 【解析】化简圆 到直线 的距离 ， 又 两圆相交. 选B 8．已知双曲线 的右焦点为 ，右顶点为 ， ， 两点在双曲线 的右 支上， 为 中点， 为 轴上一点，且 .若 ，则双曲线 的离心率的取值范 围是（ ） A． B． C． D． 【答案】．C 4【详解】解：设 ，由题意可知 ， 轴，不妨令 ， （其中 ）.因为 ，所以 ，解得 . 由题易知 ，整理得 ，即 ，即 ，又 ，所以 .故选C. 二、单选题（本大题共4小题，每小题5分，共20分．） 9.设P是椭圆C： 上任意一点，F，F 是椭圆C的左、右焦点，则（ ） 1 2 A PF＋PF＝ B. ﹣2＜PF﹣PF＜2 C. 1≤PF·PF≤2 D. 0≤ ≤1 1 2 1 2 1 2 【答案】ACD 【详解】椭圆长轴长为 ，根据椭圆定义 ，故选A； 设P是椭圆C的任意一点，则 ，所以 ，B错误； ,而 ，所以 ，C正确； ,又根据椭圆性质 有 ，所以 ，D正确。故选:ACD. 10．若直线过点A(1,2)，且在两坐标轴上截距的绝对值相等，则直线l方程可能为( ) A．x y10 B．x y30 C．2x y0 D．x y10 【答案】ABC 20 【解析】：当直线经过原点时，斜率为k  2，所求的直线方程为y2x，即2x y0； 10 5当直线不过原点时，设所求的直线方程为 x yk，把点 A(1,2)代入可得12k，或12k ，求得 k 1，或k 3，故所求的直线方程为x y10，或x y30； 综上知，所求的直线方程为2x y0、x y10，或x y30．故选：ABC． 11. 已知P是椭圆 上一点，椭圆的左、右焦点分别为 ，且 ，则 （ ） A． 的周长为12 B． C．点P到x轴的距离为 D． 【答案】. 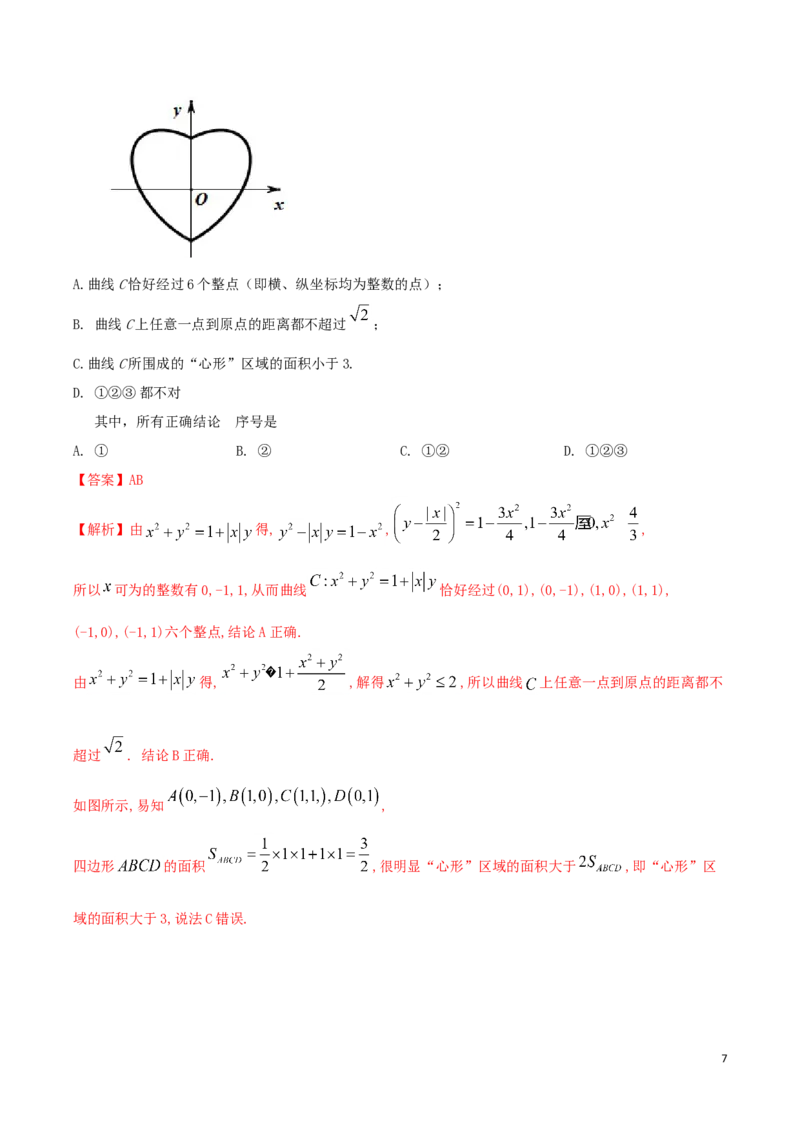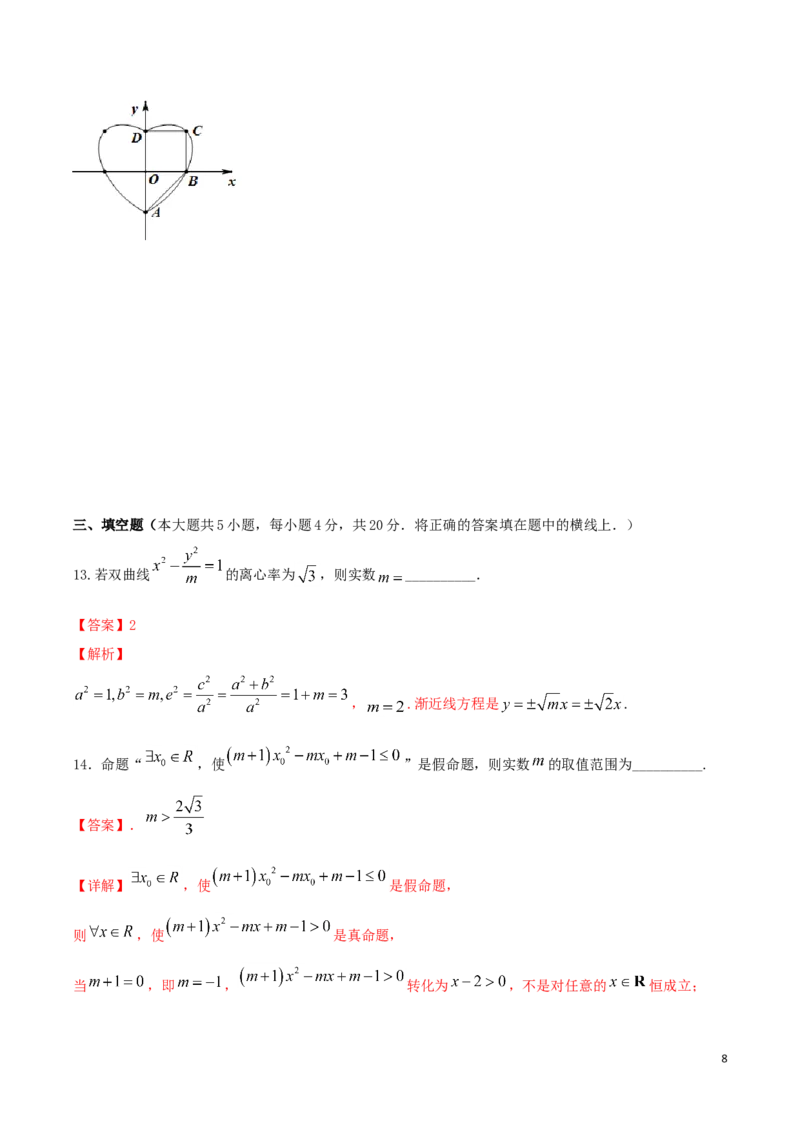BCD 【详解】由椭圆方程知 ，所以 ，所以 ， 于是 的周长为 ，故A选项错误；在 中，由余弦定理可得 ， 所以 ，解得 ， 故 ，故B选项正确； 设点 到 轴的距离为 ，则 ， 所以 ，故C选项正确； ，故D选项正确． 12.数学中有许多形状优美、寓意美好的曲线，曲线C： 就是其中之一（如图）.给出下 列三个结论： 6A.曲线C恰好经过6个整点（即横、纵坐标均为整数的点）； B. 曲线C上任意一点到原点的距离都不超过 ； C.曲线C所围成的“心形”区域的面积小于3. D. ①②③都不对 其中，所有正确结论 的序号是 A. ① B. ② C. ①② D. ①②③ 【答案】AB 【解析】由 得, , , 所以 可为的整数有0,-1,1,从而曲线 恰好经过(0,1),(0,-1),(1,0),(1,1), (-1,0),(-1,1)六个整点,结论A正确. 由 得, ,解得 ,所以曲线 上任意一点到原点的距离都不 超过 . 结论B正确. 如图所示,易知 , 四边形 的面积 ,很明显“心形”区域的面积大于 ,即“心形”区 域的面积大于3,说法C错误. 7三、填空题（本大题共5小题，每小题4分，共20分．将正确的答案填在题中的横线上．） 13.若双曲线 的离心率为 ，则实数 __________． 【答案】2 【解析】 ， .渐近线方程是 . 14．命题“ ，使 ”是假命题，则实数 的取值范围为__________. 【答案】． 【详解】 ，使 是假命题， 则 ，使 是真命题， 当 ，即 ， 转化为 ，不是对任意的 恒成立； 8当 ， ，使 即恒成立，即 ，第二个式子化简得 ， 解得 或 所以 15.曲线 是平面内与两个定点 和 的距离的积等于常数 的点的轨迹,给出下列 三个结论:①曲线 过坐标原点；②曲线 关于坐标原点对称; ③若点 在曲线 上,则 ,的面积 不大于 ，其中，所有正确结论的序号是_____ 【答案】②③ 【解析】 【详解】设曲线 上点的坐标为 ，则 ①将 代入曲线方程知： 曲线 不过坐标原点，①错误； ②若 在曲线 上，将 代入曲线方程，可知方程成立，则曲线 关于坐标原点对称，②正确； ③ ，③正确. 故答案为：②③ 16．已知椭圆 （ ）的离心率为 ，短轴长为2，点P为椭圆上任意一点，则 的最小值是______. 【答案】． 9【详解】据题意 ， ，解得 ， ，于是 ， 所以 ， 当且仅当 ，即 ， 时等号成立.故答案为： . 三、解答题（本大题共6小题，共70分．解答须写出文字说明、证明过程或演算步骤．） 17．（10分）分别求适合下列条件的方程： （1）焦点在 轴上，长轴长为 ，焦距为 的椭圆标准方程； （2）一个焦点为 ，渐近线方程为 的双曲线标准方程. 【详解】（1）由已知条件可得 ，可得 ， ， 因此，所求椭圆的标准方程为 ； （2）设所求双曲线的方程为 ，化为标准方程得 ， 由于该双曲线的一个焦点坐标为 ，则 ，解得 ， 因此，该双曲线的标准方程为 . 18．已知圆 经过三点 ， ， . （Ⅰ）求圆 的方程； （Ⅱ）求过点 且被圆 截得弦长为 的直线的方程. 10【答案】（Ⅰ） ； （Ⅱ） 和 . 【解析】（Ⅰ）由题意，设圆 的方程为 ，列出方程组，求解 的值，即 可求解； （Ⅱ）由（Ⅰ）知圆心坐标为 ，半径为 ，弦长为 时，得到圆心到直线的距离为 ，利用点到直 线的距离公式，列出方程，求得直线的斜率，即可求求解. 【详解】 （Ⅰ）由题意，设圆 的方程为 ， 则 ，解得 ， 所以圆 的方程为 . （Ⅱ）由（Ⅰ）知圆心坐标为 ，半径为 ，弦长为 时，圆心到直线的距离为： . ①若直线斜率不存在，直线方程为 ，经检验符合题意； ②若直线斜率存在，设直线斜率为 ，则直线方程 ， 即 ，则 ，解得 ， 所以直线方程为 ，即 . 综上可知，直线方程为 和 . 19．已知椭圆 的离心率为 ，椭圆上任意一点到右焦点F的距离的最大值为 11（1）求椭圆的方程； （2）已知点 是线段 上一个动点(O为坐标原点)，是否存在过点 且与 轴不垂直的直线 与 椭圆交于 ， 点，使得 ？并说明理由 【答案】（1） ；（2）当 时，存在这样的直线 ， ， 当 ，不存在；证明见解析 【解析】（1）结合已知条件 ，可求 ， ，由 ，可以求 的值，进而可求椭 圆的方程. （2）有题意可知 ，假设存在满足条件的直线 ，设 的方程为 ，代入 ， 设 ， ，根据根与系数的关系可以求 ，根据 ，从而 可求 的中点为 ，由 可得 ，可得 ， 之间的关系，结合 的范围可 求 . 【详解】 由题意可得 ，解得： ， 又因为 ，所以 ， 所以椭圆的方程为 ， 12（2）由（1）得 ，所以 ，假设存在满足条件的直线 ， 设 的方程为 ，代入 ，得 ， 设 ， ，则 ， ， ， 设 的中点为 ，则 ， 因为 ，所以 ，所以 ， 即 ， 所以 ， 当 时， ，即存在这样的直线 ， 当 时， 不存在，即不存在这样的直线 . 20．（12分）已知命题 ；命题 ． （1）若 ，“ 或 ”为真命题，“ 且 ”为假命题，求实数 的取值范围． （2）若 是 的充分条件，求实数 的取值范围． 【详解】由 得 ， ， 设 （1） 时 ，由已知可知 与 一真一假 13若 为真命题， 为假命题，则 ，所以 若 假命题， 为真命题，则 ， 则 ， 综上： （2）根据题意知： 是 的充分条件， 是 的充分条件，即 ，解得 ，所以实数 的取值范围 . 21．已知椭圆 ： 的离心率为 ，椭圆的四个顶点围成的四边形的面积为4. （Ⅰ）求椭圆 的标准方程； （Ⅱ）直线 与椭圆 交于 ， 两点， 的中点 在圆 上，求 （ 为坐标原点） 面积的最大值. 【答案】（Ⅰ） . （Ⅱ）1. 【解析】【详解】试题分析：（Ⅰ）由题意知， ，得 ， ，代入椭圆的方程，再 由椭圆 的四个顶点围成的四边形的面积得 ，求得 的值，即可得到椭圆的方程； （Ⅱ）当直线 的斜率不存在时，得到 ， 当直线 的斜率存在时，设 : ，联立方程组，求得 ，求得 中点的坐标，代入圆 14的方程，得 ，再由弦长公式和点到直线的距离公式，即可得到 的表达式，即可求解 面积的最大值． 试题解析： （Ⅰ）由题意知 ，得 ， ， 所以 ， 由椭圆 的四个顶点围成的四边形的面积为4，得 ， 所以 ， ，椭圆 的标准方程为 . （Ⅱ）当直线 的斜率不存在时， 令 ，得 ， ， 当直线 的斜率存在时，设 : ， ， ， ， 由 ，得 ， 则 ， ， 所以 ， ， 将 代入 ，得 ， 又因为 ， 15原点到直线 的距离 ， 所以 . 当且仅当 ，即 时取等号. 综上所述， 面积的最大值为1. 22．（12分）已知定圆 ,动圆 过点 ,且和圆 相切． （1）求动圆圆心 的轨迹 的方程； （2）设不垂直于 轴的直线 与轨迹 交于不同的两点 、 ，点 ．若 、 、 三点不共线, 且 ．证明：动直线 经过定点． 【详解】(1)圆 的圆心为 ,半径 . 设动圆 的半径为 ,依题意有 ．由 ,可知点 在圆 内,从而圆 内切于圆 ,故 , 16即 .所以动点 的轨迹E是以 、 为焦点,长轴长为4的椭圆, 其方程为 (2) 设直线 的方程为 ,联立 消去 得, , . 设 , , 则 , . 于是 , 由 知 . 即 ,得 , . 故动直线 的方程为 ,过定点 . 17