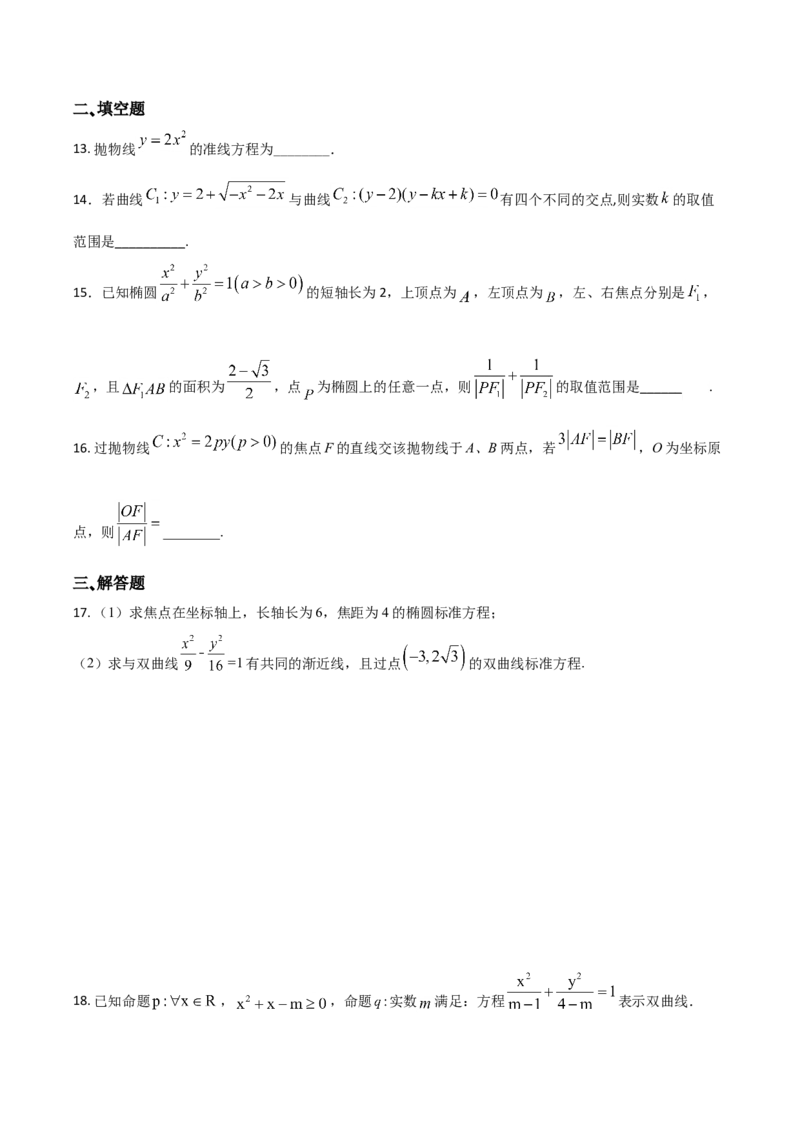文档内容
高二(上)期末模拟测试卷(B 卷 能力提升)
考试时间:120分钟 满分:150分
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目
要求的.)
1. 已知方程 表示焦点在 轴上的椭圆,则 的取值范围是( )
A. B. C. D. 且
2. 下列四个命题为真命题的是
A. “若 ,则 互为相反数”的逆命题;
B. “全等三角形的面积相等” 的否命题;
C. “若 ,则 无实根”的逆否命题;
D. “不等边三角形的三个内角相等”的逆命题;
3. 王昌龄《从军行》中两句诗为“黄沙百战穿金甲,不破楼兰终不还”,其中后一句中“攻破楼兰”是
“返回家乡”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4. 已知双曲线 的一条渐近线过点 ,且双曲线的一个焦点在抛物线
的准线上,则双曲线的方程为( )
A. B. C. D.
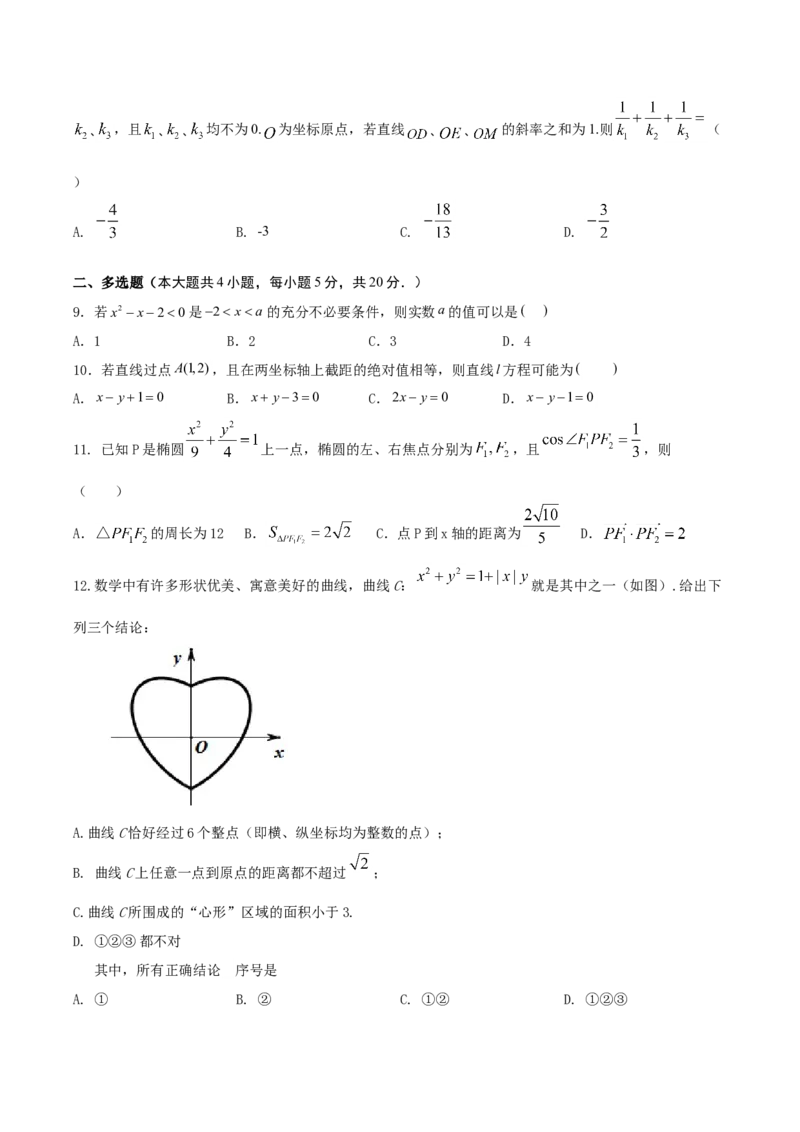
5. 如图图为中国古代刘徽的《九章算术注》中研究“勾股容方”问题的图形,图中 为直角三角形,
四边形 为它的内接正方形,已知 , ,在 上任取一点,则此点取自正方形
的概率为( )A. B. C. D.
6. 已知点P为双曲线 右支上一点,点F,F 分别为双曲线的左右焦点,点I是
1 2
△PFF 的内心(三角形内切圆的圆心),若恒有 成立,则双曲线的离心率取值
1 2
范围是( )
A. (1, ) B. (1,2 )
C. (1,2 ] D. (1, ]
7. 试在抛物线 上求一点 ,使其到焦点 的距离与到 的距离之和最小,则该点坐标为
A. B. C. D.
8. 已知椭圆 : 的右焦点为 ,且离心率为 ,三角形 的三个顶点都
在椭圆 上,设它的三条边 、 、 的中点分别为 、 、 ,且三条边所在直线的斜率分别为 、、 ,且 、 、 均不为0. 为坐标原点,若直线 、 、 的斜率之和为1.则 (
)
A. B. -3 C. D.
二、多选题(本大题共4小题,每小题5分,共20分.)
9.若x2 x20是2xa的充分不必要条件,则实数a的值可以是( )
A.1 B.2 C.3 D.4
10.若直线过点A(1,2),且在两坐标轴上截距的绝对值相等,则直线l方程可能为( )
A.x y10 B.x y30 C.2x y0 D.x y10
11. 已知P是椭圆 上一点,椭圆的左、右焦点分别为 ,且 ,则
( )
A. 的周长为12 B. C.点P到x轴的距离为 D.
12.数学中有许多形状优美、寓意美好的曲线,曲线C: 就是其中之一(如图).给出下
列三个结论:
A.曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
B. 曲线C上任意一点到原点的距离都不超过 ;
C.曲线C所围成的“心形”区域的面积小于3.
D. ①②③都不对
其中,所有正确结论 的序号是
A. ① B. ② C. ①② D. ①②③二、填空题
13. 抛物线 的准线方程为________.
14.若曲线 与曲线 有四个不同的交点,则实数 的取值
范围是__________.
15.已知椭圆 的短轴长为2,上顶点为 ,左顶点为 ,左、右焦点分别是 ,
,且 的面积为 ,点 为椭圆上的任意一点,则 的取值范围是______ .
16. 过抛物线 的焦点F的直线交该抛物线于A、B两点,若 ,O为坐标原
点,则 ________.
三、解答题
17. (1)求焦点在坐标轴上,长轴长为6,焦距为4的椭圆标准方程;
(2)求与双曲线 =1有共同的渐近线,且过点 的双曲线标准方程.
18. 已知命题 , ,命题 实数 满足:方程 表示双曲线.若命题 为真命题,求实数 的取值范围;
1
若命题“ 或 ”为假命题,求实数 的取值范围.
219. 已知抛物线 的焦点为 ,点 在抛物线上,且点 的横坐标为 , .
(1)求抛物线的方程;
的
(2)设过焦点 且倾斜角为 交抛物线于 两点,求线段 的长.
20.已知双曲线C的焦点在坐标轴上,其渐近线方程为 ,过点 .
(1)求双曲线C的标准方程;
(2)是否存在被点 平分的弦?如果存在,求出弦所在的直线方程;如果不存在,请说明理由.21.已知椭圆 ,直线 不过原点 且不平行于坐标轴, 与 有两个交点 , ,
线段 的中点为 .
(Ⅰ)证明:直线 的斜率与 的斜率的乘积为定值;
(Ⅱ)若 过点 ,延长线段 与 交于点 ,四边形 能否为平行四边形?若能,求此时
的斜率,若不能,说明理由.
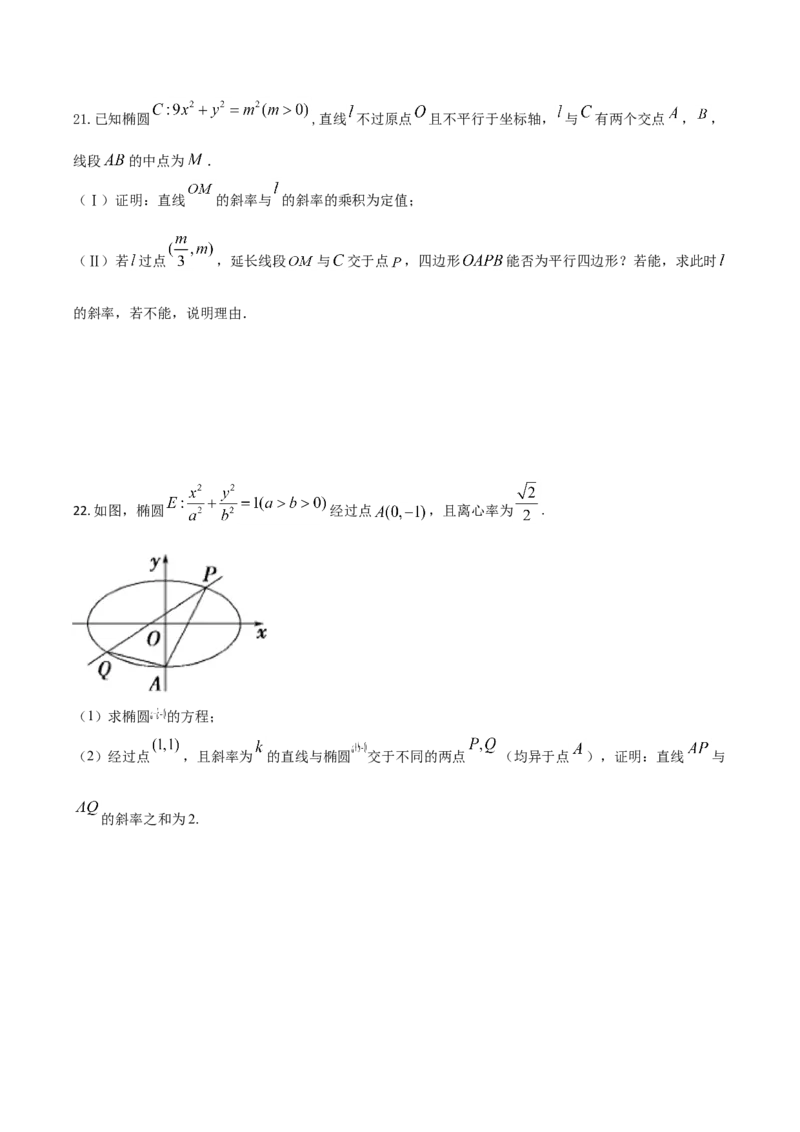
22. 如图,椭圆 经过点 ,且离心率为 .
(1)求椭圆 的方程;
(2)经过点 ,且斜率为 的直线与椭圆 交于不同的两点 (均异于点 ),证明:直线 与
的斜率之和为2.