数学（理科）_2024年2月_01每日更新_29号_2024届四川省射洪中学高三下学期开学考试_四川省射洪中学2023-2024学年高三下学期开学考试数学（理）PDF版含答案（可编辑）

射洪中学高2021级高三下期入学考试 数学(理科)试题 命题人：杨 勇 审题人：文质彬 时间：120分钟满分：150分 第I卷(选择题共60分) 注意事项： 1.答卷前，考生务必将自己的姓名、准考证号等填写在答题卡上。 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后， 再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。 3.考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求 的，请将答案涂在答题卡上。 1. 已知集合M= x x−1    <2  ,N=−1,0,1,2,3  ，则M∩N= A. 0,1,2  B. 1,2  C. -1,0,1,2  D. 2,3  3−2i 2. 若复数z满足z= ，其中i为虚数单位，则z 2+3i  = A.0 B.-1 C. 13 D.1 3. 下图是遂宁市2022年4月至2023年3月每月最低气温与最高气温(℃)的折线统计图：已知每月最低气 温与最高气温的线性相关系数r=0.88，则下列结论正确的是 A.月温差(月最高气温-月最低气温)的最大值出现在8月 B.每月最低气温与最高气温有较强的线性相关性，且二者为线性负相关 C. 每月最高气温与最低气温的平均值在4-8月逐月增加 D.9-12月的月温差相对于5-8月，波动性更小 4. 下列说法不正确的是 A.若am20，则¬p：∃x ∈R，2x0<0 0  C.回归直线方程为y=1.23x+0.08，则样本点的中心可以为4,5  D.在△ABC中，角A,B,C的对边分别为a,b,c则“A>B”是“sinA>sinB”的充要条件 2x-y-2≤0,  5. 已知实数x，y满足x-2y-2≥0,则y-3x的最小值是 x≥0, 8 A.- B.-2 C.-1 D.1 3 高三数学（理科）入学考试试题 第1页（共4页）6. 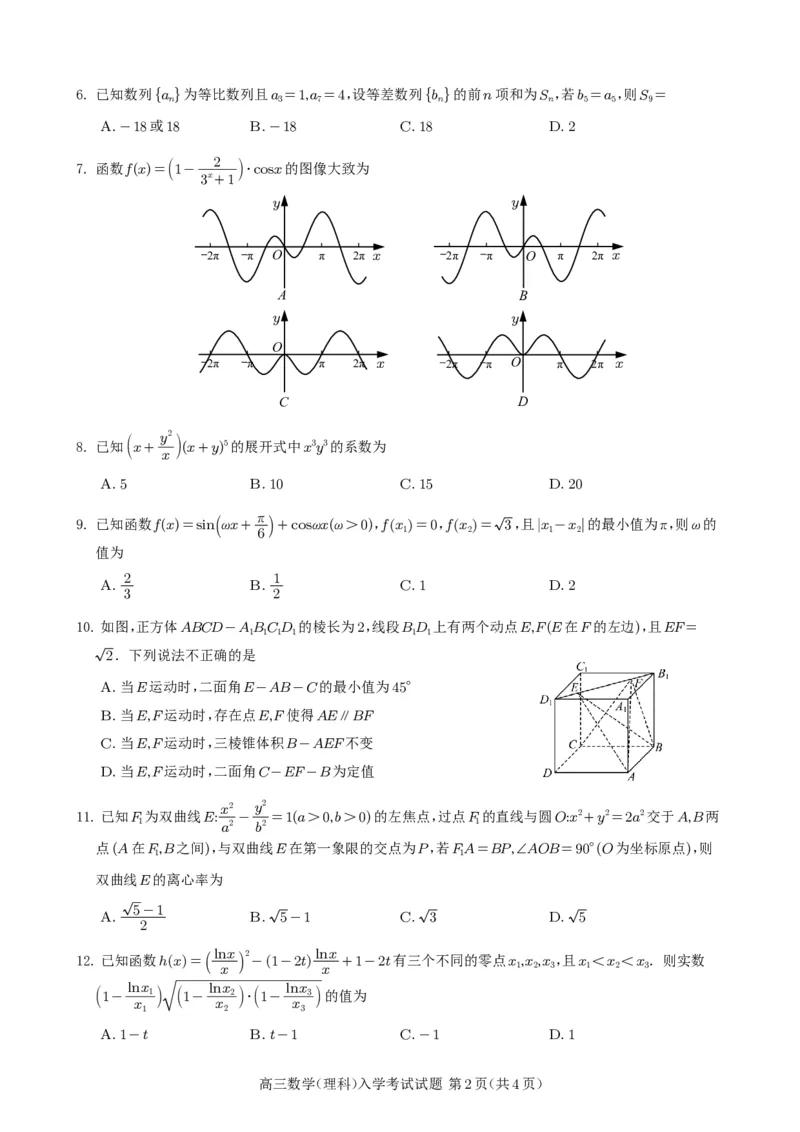已知数列a n  为等比数列且a =1,a =4，设等差数列b 3 7 n  的前n项和为S ，若b =a ，则S = n 5 5 9 A.-18或18 B.-18 C.18 D.2 2 7. 函数f(x)=1- 3x+1  ⋅cosx的图像大致为 y y 2π π O π 2π x 2π π O π 2π x A B y y O 2π π π 2π x 2π π O π 2π x C D y2 8. 已知x+ x  (x+y)5的展开式中x3y3的系数为 A.5 B.10 C.15 D.20 π 9. 已知函数f(x)=sinωx+ 6  +cosωx(ω>0)，fx 1  =0，fx 2  = 3，且x 1 -x 2  的最小值为π，则ω的 值为 2 1 A. B. C.1 D.2 3 2 10.如图，正方体ABCD-ABCD 的棱长为2，线段BD 上有两个动点E,F(E在F的左边)，且EF= 1 1 1 1 1 1 2．下列说法不正确的是 A.当E运动时，二面角E-AB-C的最小值为45° B.当E,F运动时，存在点E,F使得AE⎳BF C.当E,F运动时，三棱锥体积B-AEF不变 D.当E,F运动时，二面角C-EF-B为定值 x2 y2 11.已知F 为双曲线E: - =1(a>0,b>0)的左焦点，过点F 的直线与圆O:x2+y2=2a2交于A,B两 1 a2 b2 1 点(A在F,B之间)，与双曲线E在第一象限的交点为P，若FA=BP,∠AOB=90°(O为坐标原点)，则 1 1 双曲线E的离心率为 5-1 A. B. 5-1 C. 3 D. 5 2 12.已知函数hx  lnx = x  2 -1-2t  lnx +1-2t有三个不同的零点x,x ,x ，且x 0)的焦点为F，准线为l，点Q(2,y )在抛物线上，点K为l与y轴的交点， 0 且QK  = 2QF  ，过点P4,2    向抛物线作两条切线，切点分别为A,B，则AF⋅BF=________. 三、解答题：共70分．第17题至第21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生 根据要求作答． 17.本小题12分  已知数列a n  前n项和为S ．从下面①②中选择其中一个作为条件解答试题，若选择 n 不同条件分别解答，则按第一个解答计分． ①数列a n  是等比数列，S =6，且4a ,2a ,a 成等差数列； 2 2 3 4 ②数列a n  是递增的等比数列，aa =32，a +a =12； 1 4 2 3 (1)求数列a n  的通项公式； (2)已知数列b n  1 的前n项的和为T，且b = n n log 2 a n  ⋅log 2 a n+1  ．证明：T <1． n 18.本小题12分  某企业举行招聘考试，共有1000人参加，分为初试和复试，初试成绩总分100分，初试通 过后参加复试． (1)若所有考生的初试成绩X近似服从正态分布Nμ,σ2  ，其中μ=65，σ=15，试估计初试成绩不低于 80分的人数；(精确到个位数) (2)复试共三道题，每答对一题得10分，答错得0分，答完三道题后的得分之和为考生的复试成绩．已知 3 3 某考生进入复试，他在复试中第一题答对的概率为 ，后两题答对的概率均为 ，且每道题回答正确与 4 5 否互不影响．记该考生的复试成绩为Y，求Y的分布列及期望. 附：若随机变量X服从正态分布Nμ,σ2  ，则：Pμ-σb>0 a2 b2  的左、右顶点为A,A ，点G是椭圆C的上顶点，直 1 2 8 2 线A G与圆x2+y2= 相切，且椭圆C的离心率为 2 3 2 (1)求椭圆C的标准方程；   (2)若点Q在椭圆C上，过左焦点F 的直线l与椭圆C交于A,B两点(A,B不在x轴上)且OQ⋅AB=0, 1 2 2AB (O为坐标原点)，求  OQ  的取值范围． 2 21.本小题12分  e2x 已知函数f(x)= ，其中x>0，a∈R． xa (1)求函数fx  的单调区间； f(x) (2)当a>0时，函数g(x)=alnx+ -2x+1恰有两个零点，求a的取值范围． e2 选考题：共10分，请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分． 【选修4-4：坐标系与参数方程】 22.本小题10分  在直角坐标系xoy中，已知曲线C 1 :   x y= = 2 2 s + in 2 θ cosθ (θ为参数，θ∈0,π  )，在极坐标系 π 中，曲线C 是以1, 2 2  为圆心且过极点O的圆． (1)分别写出曲线C 普通方程和曲线C 的极坐标方程； 1 2 π (2)直线l:θ= ρ∈R 4  与曲线C 1 、C 2 分别交于M、N两点(异于极点O)，求MN  ． 【选修4-5：不等式选讲】 23.本小题10分  已知函数fx  =x-t  +x+t  ，t∈R． (1)若t=1，求不等式fx  ≤8-x2的解集； (2)已知m+n=4，若对任意x∈R，都存在m>0，n>0使得fx  4m2+n = ，求实数t的取值范围. mn 高三数学（理科）入学考试试题 第4页（共4页）