文档内容
临川一中 2024 届高三“九省联考”考后适应性测试数学试题一
本套试卷根据九省联考题型命制,题型为8+3+3+5模式
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要
求的.
1.(本题5分)某校高一年级18个班参加艺术节合唱比赛,通过简单随机抽样,获得了10个班的比赛得
分如下:91,89,90,92,94,87,93,96,91,85,则这组数据的80%分位数为( )
A.93 B.93.5 C.94 D.94.5
π
2.(本题5分)已知向量a,b满足a⋅b =1, a,b = ,则 a+b +2 a−b 的最小值为( )
3
A. 6+2 2 B. 6+ 2 C.8 D.2
3.(本题5分)过直线y=x上一点M作圆C:(x−2)2+y2 =1的两条切线,切点分别为P,Q.若直线PQ
过点(1,3),则直线PQ的方程为( )
A.5x−y−2=0 B.x−5y+14=0
C.5x+y−8=0 D.x+5y−16=0
4.(本题5分)古城赣州最早有五大城门,分别为镇南门、百盛门、涌金门、建春门和西津门,赣州某学
校历史兴趣小组决定利用两个周日的时间对五大城门的地理位置及历史意义进行调研.若约定:每个城门
只调研一次,且每个周日只调研五大城门中的两大城门或三大城门,则恰好在同一个周日调研百盛门和建
春门的概率为( )
2 1 1 4
A. B. C. D.
5 3 5 5
5.(本题5分)数列{a }的前n项和为S ,满足S +a =1024,则数列{a }的前n项积的最大值为( )
n n n n n
A.255 B.245 C.29 D.210
6.(本题5分)已知矩形ABCD中,AB=2,BC=1,将△CBD沿BD折起至C′BD,当C′B与AD所成角
最大时,三棱锥C′− ABD的体积等于( )
3 3 2 5 2 5
A. B. C. D.
6 2 15 5
7.(本题5分)已知cos(140°−α)+sin(110°+α)=sin(130°−α),求tanα=( )
3 3
A. B.− C. 3 D.− 3
3 3
8.(本题5分)若存在a∈R,使得对于任意x∈
1 ,e
,不等式lnx≤ax2+bx≤ ( e2−2e ) lnx+e恒成立,则
e
试卷第1页,共4页
学科网(北京)股份有限公司实数b的最小值为( )
e3+e+1 e2+e
A.− B.− C.−1 D.−e
e2−1 e2−1
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9.(本题6分)下列说法正确的是( )
A.∅∈{0}
x
B.集合{x|x=2n,n∈Z}=x ∈Z
2
1 x∈Q
C.函数 f (x)= 的值域为[0,1]
0 x∈ Q
R
D. f (x)=x x 在定义域内单调递增
10.(本题6分)如图,点A,B,C是函数 f (x)=sin(ωx+ϕ)(ω>0)的图象与直线y= 3 相邻的三个交点,
2
π π
且 BC − AB = , f − =0,则( )
3 12
A.ω4
9π 1
B. f =
8 2
π π
C.函数 f (x)在 , 上单调递减
3 2
π
D.若将函数 f (x)的图象沿x轴平移θ个单位,得到一个偶函数的图像,则θ的最小值为
24
11.(本题6分)已知定义在(0,+∞)的函数 f (x)满足:①对∀x∈(0,+∞)恒有xf′(x)− f (x)=x;②对任意的
正数m,n恒有 f (mn)=nf (m)+mf (n)+mn.则下列结论中正确的有( )
A. f (1)=−1
B.过点
(
e, f
(e))
的切线方程y=x−1
C.对∀x∈(0,+∞),不等式 f (x)≥x−e恒成立
试卷第2页,共4页D.若x 为函数y= f (x)+x2的极值点,则 f (x )+3x >0
0 0 0
三、填空题:本题共3小题,每小题5分,共15分.
12.(本题5分)已知复平面上一个动点Z对应复数z,若|z−4i|≤2,其中i是虚数单位,则向量OZ扫过
的面积为 .
m2
13.(本题5分)已知实数x,y满足x2−3lnx−y=0,则 x2+y2−mx+my+ (m∈R)的最小值为 .
2
14.(本题5分)如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,动点M
在边DC上(不同于D点),P为边AB上任意一点,沿AM将 ADM翻折成 AD'M,当平面AD'M垂直于
平面ABC时,线段PD'长度的最小值为 . △ △
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
2
15.(本题13分)某校举行围棋友谊赛,甲、乙两名同学进行冠亚军决赛,每局比赛甲获胜的概率是 ,
3
1
乙获胜的概率是 ,规定:每一局比赛中胜方记1分,负方记0分,先得3分者获胜,比赛结束.
3
(1)求进行3局比赛决出冠亚军的概率;
(2)若甲以2:1领先乙时,记X 表示比赛结束时还需要进行的局数,求X 的分布列及数学期望.
16.(本题15分)设函数 f (x)=lnx+ax+b,曲线y= f (x)在点 ( 1, f (1)) 处的切线方程为y=6x−3.
(1)求a,b;
3
(2)证明: f (x)>− .
5x
17.(本题15分)如图,AB是半球O的直径,AB=4,M,N依次是底面
AB
上的两个三等分点,P是半球
面上一点,且∠PON =60°.
试卷第3页,共4页
学科网(北京)股份有限公司(1)证明:PB⊥PM ;
(2)若点P在底面圆上的射影为ON中点,求直线PM与平面PAB所成的角的正弦值.
x2
18.(本题17分)已知双曲线C: − y2 =1,点M(4,0),经过点M的直线交双曲线C于不同的两点A、B,
4
过点A,B分别作双曲线C的切线,两切线交于点E.(二次曲线Ax2+By2 =1在曲线上某点(x ,y )处的切
0 0
线方程为Ax x+By y=1)
0 0
(1)求证:点E恒在一条定直线L上;
(2)若两直线与L交于点N,AN =λMA,BN =µMB,求λ+µ的值;
(3)若点A、B都在双曲线C的右支上,过点A、B分别做直线L的垂线,垂足分别为P、Q,记AMP,BMQ,
PMQ的面积分别为S ,S ,S ,问:是否存在常数m,使得SS =mS2?若存在,求出m的值;若不存在,
1 2 3 1 2 3
请说明理由.
19.(本题17分)若各项为正的无穷数列{a }满足:对于∀n∈N*,a2 −a2 =d,其中d为非零常数,则称
n n+1 n
数列{a }为D数列.记b =a −a .
n n n+1 n
(1)判断无穷数列a = n和a =2n是否是D数列,并说明理由;
n n
(2)若{a }是D数列,证明:数列{b }中存在小于1的项;
n n
n 1
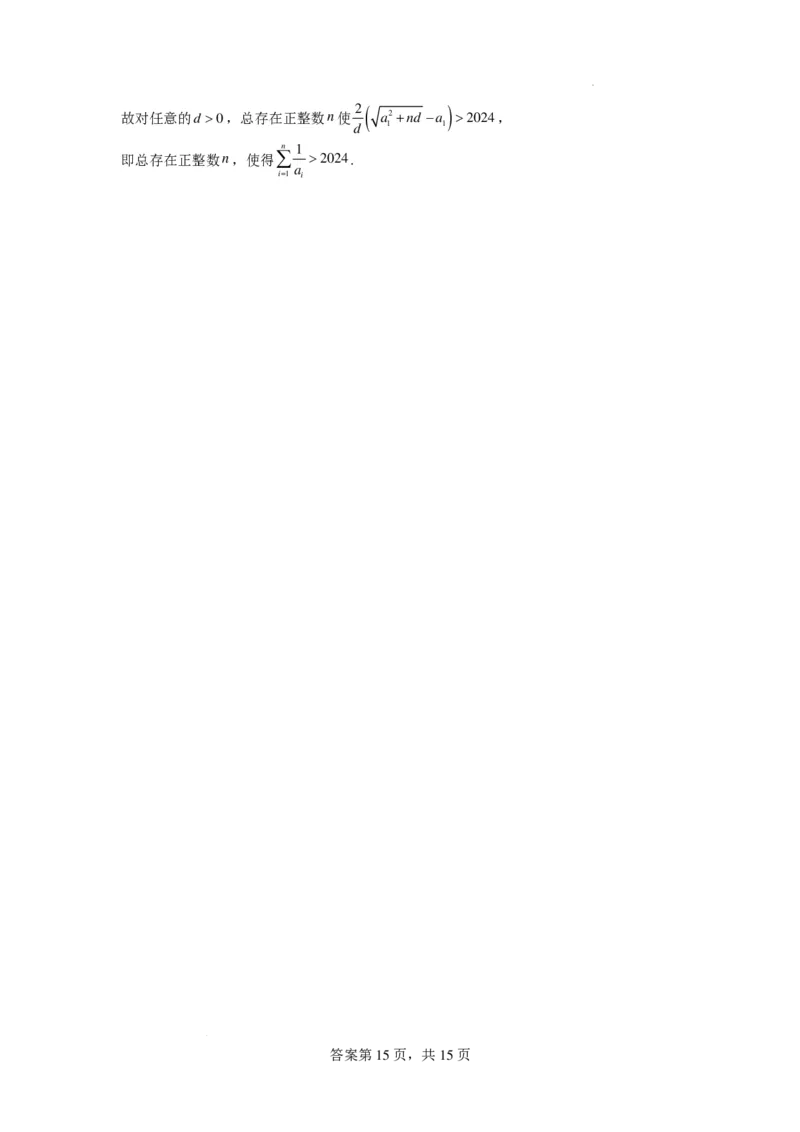
(3)若{a }是D数列,证明:存在正整数n,使得∑ >2024.
n a
i=1 i
试卷第4页,共4页参考答案:
1.B
【详解】将比赛得分从小到大重新排列:85,87,89,90,91,91,92,93,94,96,
因为10×80%=8,
93+94
所以这组数据的80%分位数第8个数与第9个数的平均值,即 =93.5.
2
故选:B.
2.A
【详解】解:建立如图所示的平面直角坐标系,设OA=a,OB=b且 OA =m,OB =n,
π 1 3
因为a,b = ,可得A(m,0),B( n, n),
3 2 2
1 3
则a=OA=(m,0),b=OB=( n, n),
2 2
1 3 1 3
所以a+b=(m+ n, n),a−b=(m− n,− n),
2 2 2 2
1
又因为向量a,b满足a⋅b =1,可得a⋅b = a b cosa,b = mn=1,解得mn=2,
2
1 3
所以 a+b = (m+ n)2+( n)2 = m2+n2+mn = m2+n2+2,
2 2
1 3
a−b = (m− n)2+(− n)2 = m2+n2−mn = m2+n2−2,
2 2
则 a+b +2 a−b = m2+n2+2+2 m2+n2−2,
设t=m2+n2,因为t =m2+n2 ≥2mn=4,当且仅当 m=n= 2 ,
所以 a+b +2 a−b = t+2+2 t−2,
又因为 f (t)= t+2+2 t−2在[4,+∞)上为单调递增函数,
所以 f (t) = f (4)= 6+2 2,即 a+b +2 a−b 的最小值为 6+2 2.
min
故选:A.
3.C
答案第1页,共15页
学科网(北京)股份有限公司【详解】圆C:(x−2)2+y2 =1的圆心为C(2,0),
设M(t,t),则以MC为直径的圆的方程为
t+2 2 t 2 1
x− +y− = (t−2)2+(t−0)2
2 2 4
与圆C的方程(x−2)2+y2 =1两式相减可得直线PQ的方程为
(t−2)x+ty−2t+3=0
1
因为直线PQ过点(1,3),所以t−2+3t−2t+3=0,解得t =− .
2
5 1
所以直线PQ的方程为− x− y+1+3=0,即5x+y−8=0.
2 2
故选:C.
4.A
【详解】由题意,每个城门只调研一次,且每个周日只调研五大城门中的两大城门或三大城
门,
共有C2+C3 =20种不同的调研方法,
5 5
其中恰好在同一个周日调研百盛门和建春门,可得分为:
①其中一个周日只调研百盛门和建春门,另一个周日调研其他三门,有C1 =2种方法;
2
②其中一个周日调研百盛门、建春门和其中另一个门,另一个周日调研剩余的两门,
有C1C1 =6种方法,共有2+6=8种不同的调研方法,
2 3
8 2
所以恰好在同一个周日调研百盛门和建春门的概率为P= = .
20 5
故选:A.
5.B
【详解】依题意,n∈N∗,S +a =1024,则a =512,当n≥2时,S +a =1024,
n n 1 n−1 n−1
答案第2页,共15页两式相减得2a =a ,即a = 1 a ,因此数列{a }是以512为首项, 1 为公比的等比数列,
n n−1 n 2 n−1 n 2
1
于是a =512×( )n−1 =210−n,显然数列{a }单调递减,当n≤10时,a ≥1,当n≥11,a <1,
n 2 n n n
所以当n=9或n=10时,数列{a }的前n项积最大,最大值为29×28×27××22×2×20
=245.
n
故选:B
6.A
π
【详解】因为异面直线所成角的范围是0,
,故当C′B⊥ AD时,C′B与AD所成角最大,
2
因为四边形ABCD是矩形,所以AB⊥AD,
而AB∩C′B=B,AB,C′B⊂平面ABC′,所以AD⊥平面ABC′,
因为AC′⊂平面ABC′,所以AD⊥AC′,
在直角三角形ADC′中,AD=1,C′D=2,AC′= 3,
而BC′=1,AB=2,BC′2+AC′2 = AB2,所以BC′⊥ AC′,
1 1 1 3
所以V =V = S ⋅AD= × ×1× 3×1= .
C′−ABD D−ABC′
3
ABC′
3 2 6
故选:A
7.D
【详解】由题意知,cos(140°−α)+sin(110°+α)=sin(130°−α)
即−cos(40°+α)+cos(20°+α)=cos(40°−α),
故cos(20°+α)=cos(40°−α)+cos(40°+α),
即cos20°cosα−sin20°sinα=2cos40°cosα,
故cos20°cosα−2cos40°cosα=sin20°sinα,
sinα cos20°−2cos40° cos(30°−10°)−2cos(30°+10°)
即tanα= = =
cosα sin20° sin20°
3 3
− cos10°+ sin10°
2 2
3sin(10°−30°) − 3sin20° ,
= = = =− 3
sin20° sin20° sin20°
答案第3页,共15页
学科网(北京)股份有限公司故选:D
8.C
lnx 1 1−lnx
【详解】令 f (x)= ,其中x∈
,e
,则 f′(x)= ,
x e x2
当 1 < x0,g′(e)=− 1 <0,
e e
1
所以,存在x ∈ ,e,使得g′(x )=0,
0 e 0
1
当 0,此时函数g(x)单调递增,
e 0
当x 3,1+2lnx≤3,
e x
e
所以,2(e−1)x+ −(1+2lnx)>0,
x
1 1
所以当x∈
,e
时,h′(x)>0,则函数h(x)在
,e
上单调递增,
e e
所以h(x)有唯一的零点1,
所以x =1,此时直线方程为y=x−1,故b =−1.
0 min
故选:C.
9.BD
【详解】对于A:∅⊆{0}或∅{0},故A错误;
对于B:{x|x=2n,n∈Z}={,−6,−4,−2,0,2,4,6,8,},
x x
又 ∈Z,令 =k∈Z,所以x=2k,k∈Z,
2 2
即 x x ∈Z ={ x x=2k,k∈Z }={,−6,−4,−2,0,2,4,6,8,},
2
x
所以{x|x=2n,n∈Z}=x ∈Z,故B正确;
2
1 x∈Q
对于C:因为 f (x)= ,所以 f (x)的值域为{0,1},故C错误;
0 x∈ Q
R
x2,x≥0
对于D: f (x)=x x = ,
−x2,x<0
因为y x2在[0,+∞)上单调递增,y=−x2在(−∞,0)上单调递增,
且 f (x)为连续函数,所以 f (x)在R上单调递增,故D正确;
故选:BD
10.ACD
3 π 2π
【详解】令 f (x)=sin(ωx+ϕ)= 得,ωx+ϕ= +2kπ或ωx+ϕ= +2kπ,k∈Z,
2 3 3
答案第5页,共15页
学科网(北京)股份有限公司π π 2π
由图可知:ωx +ϕ= +2kπ,ωx +ϕ= +2kπ+2π,ωx +ϕ= +2kπ,
A 3 C 3 B 3
1 π 1 π
所以 BC =x −x = − +2π, AB =x −x = ⋅ ,
C B ω 3 B A ω 3
π 1 2π
所以 = BC − AB = − +2π,所以ω4,故A选项正确,
3 ω 3
π π
所以 f (x)=sin(4x+ϕ),由 f − =0得sin− +ϕ=0,
12 3
π
所以− +ϕ=π+2kπ,k∈Z,
3
4π
所以ϕ= +2kπ,k∈Z,
3
4π 4π π
所以 f (x)=sin4x+ +2kπ=sin4x+ =−sin4x+ ,
3 3 3
9π 9π π 1
f =−sin + =− ,故B错误.
8 2 3 2
π π π 5π π
当x∈ , 时,4x+ ∈ ,2π+ ,
3 2 3 3 3
5π π π π
因为y=−sint在t∈ ,2π+ 为减函数,故 f (x)在 , 上单调递减,故C正确;
3 3 3 2
π
将函数 f (x)的图象沿x轴平移θ个单位得g(x)=−sin4x+4θ+ ,(θ<0时向右平移,
3
θ>0时向左平移),
π π
g(x)为偶函数得4θ+ = +kπ,k∈Z,
3 2
π kπ π
所以θ= + ,k∈Z,则θ的最小值为 ,故D正确.
24 4 24
故选:ACD.
11.ACD
【详解】∀x∈(0,+∞)恒有xf′(x)− f (x)=x,
f(x) ′ xf′(x)− f(x) 1
∴ = = ,
x x2 x
f(x)
∴可设 =lnx+C(其中C为常数),
x
又对任意的正数m,n恒有 f(mn)=nf(m)+mf(n)+mn,
f(mn) f(m) f(n)
∴对任意的正数m,n恒有 = + +1,
mn m n
∴ln(mn)+C =lnm+C+lnn+C+1,
∴C =−1,
答案第6页,共15页f(x)
∴ =lnx−1,即 f(x)=xlnx−x,
x
对于A,由上式可得 f (1)=−1,故A正确;
对于B, f′(x)=lnx,设切点为 ( x , f (x )) ,则切线斜率为k =lnx ,
0 0 0
f (x )− f (e) x lnx −x
∴lnx = 0 = 0 0 0 ,化简得elnx =x ,解x =e,
0 x −e x −e 0 0 0
0 0
所以点 ( e,f(e))就是切点,所以切线方程为y=x−e,故B错误;
对于C,令g(x)= f (x)−x+e=xlnx−2x+e,x>0,则g′(x)=lnx−1,
令g′(x)>0,可得x>e,g′(x)<0,可得00,
e e
1
所以∃x ∈ ,1使p(x)在(0,x )上单调递减,p(x)在(x ,+∞)上单调递增,
0 e 0 0
1
∴x=x 为函数p(x)的极小值点且满足lnx +2x =0,x ∈ ,1,
o 0 0 0 e
∴ f (x )+3x =x lnx +2x =−2x2+2x =2x (1−x )>0,故D正确.
o 0 0 0 0 0 0 0 0
故选:ACD.
8π
12.4 3+
3
【详解】因为|z−4i|≤2,
根据复数的几何意义,可得复数z表示以C(0,4)为圆心,以2为半径的圆C的圆面,
如图所示,过原点O作圆C的切线,切点为A,B,
π
在直角△OBC中,可得OC =4, BC =2,所以∠OCB= ,且 OB =2 3 ,
3
2π
所以∠ACB= ,
3
1 1 2π 8π
所以复数向量OZ扫过的面积为S =2× ×2 3×2+ ⋅(2π− )×22 =4 3+ .
2 2 3 3
答案第7页,共15页
学科网(北京)股份有限公司8π
故答案为:4 3+ .
3
13. 2
m2 m 2 m 2
【详解】由题意得, x2+y2−mx+my+ = x− +y+ ,
2 2 2
m m
即求曲线y=x2−3lnx上一点到 ,− 距离最小值,
2 2
m m
又因为 ,− 在直线y=−x上,
2 2
所以当曲线与直线y=−x平行时,距离取得最小值,
3 3
令y′=2x− =−1,解得x=1或x=− (舍去),
x 2
2
当x=1时,点(1,1)到直线x+y=0距离为 = 2,
2
m m
即所求曲线y=x2−3lnx上一点到 ,− 距离最小值为 2.
2 2
故答案为: 2
15
14.
2
【详解】作DH ⊥直线AM 于点H,连接PH ,则翻折后D′H ⊥AM ,
平面AD′M ⊥平面ABC,AM 为两平面的交线,
答案第8页,共15页∴D′H ⊥平面ABC,∴ PD′ = D′H 2+ PH 2 .
设∠DAH =θ,由 DA =2,得 DH =2sinθ, AH =2cosθ,
设 AP =x,则x∈[0,1].
2π
由 AC = CD = DA =2知ACD为正三角形,则∠BAD= ,
3
2π
∴∠BAM = −θ,在PAH中, PH 2 = AP2+ AH 2−2 AP ⋅ AH ⋅cos∠PAH,
3
即 PH 2 =x2−4cosθcos(
2π
−θ)x+4cos2θ,
3
∴ PD′2 =x2−4cosθcos( 2π −θ)x+4cos2θ+4sin2θ,
3
记t=2cosθcos(
2π
−θ),则 PD′2 =(x−t)2+4−t2,
3
2π π 1 π 1
由t=2cosθcos( −θ)=sin(2θ− )− ,0<θ ,得−1− 等价于xlnx>−5x2+2x− .
5x 5
设函数g(x)=xlnx,则g′(x)=1+lnx.
1 1
所以当x∈0, 时,g′(x)<0,当x∈ ,+∞时,g′(x)>0.
e e
1 1
故g(x)在0, 上单调递减,在 ,+∞上单调递增,
e e
1 1
从而g(x)在(0,+∞)上的最小值为g =− .
e e
2
3 1 2
设函数h(x)=−5x2+2x− =−5x− − ,
5 5 5
1 2 1
从而h(x)在(0,+∞)上的最大值为h =− <− .
5 5 e
3
故g(x)>h(x),即 f (x)>− .
5x
17.(1)证明见解析
10
(2)
5
【详解】(1)连接AM,OM,MN,PN ,
因为M,N依次是底面
AB
上的两个三等分点,
所以四边形OMNB是菱形,设MB∩ON =Q,则Q为ON中点,且ON ⊥MB,
答案第10页,共15页又因为OP=ON,∠PON =60°,故OPN是等边三角形,
连接PQ,则ON ⊥PQ,
又因为MB,PQ⊂面PMB,MB∩PQ=Q,所以ON ⊥面PMB,
因为PB⊂面PMB,所以ON ⊥PB,
因为M,N依次是底面 AB 上的两个三等分点,所以ON //AM ,所以AM ⊥PB,
又因为AB是半球O的直径, P是半球面上一点,所以PB⊥PA,
因为AM,PA⊂面PAM ,AM ∩PA= A,所以PB⊥面PAM ,
又因为PM ⊂面PAM ,所以PB⊥PM
(2)因为点P在底面圆上的射影为ON中点,
所以PQ⊥面AMB,
因为QM,QN ⊂面AMB,所以PQ⊥QM,PQ⊥QN,
又因为QM ⊥QN,
{ }
所以以 QM,QN,QP 为正交基底建立如图所示的空间直角坐标系,
( ) ( ) ( ) ( )
所以P 0,0, 3 ,M 3,0,0 ,B − 3,0,0 ,A 3,−2,0 ,
( ) ( ) ( )
所以PM = 3,0,− 3 ,PA= 3,−2,− 3 ,BA= 2 3,−2,0 ,
设平面PAB的法向量n=(x,y,z),
n⋅PA= 3x−2y− 3z=0 ( )
则 ,令x=1,则n= 1, 3,−1 ,
n⋅BA=2 3x−2y=0
π
设直线PM 与平面PAB所成角为θ0≤θ≤ ,
2
PM⋅n 2 3 10
则sinθ= cosPM,n = = =
PM ⋅ n 6× 5 5
10
所以直线PM与平面PAB所成角的正弦值为
5
答案第11页,共15页
学科网(北京)股份有限公司18.(1)证明见解析
(2)0
1
(3)存在m=
4
【详解】(1)证明:设E(x ,y ),A(x,y ),B(x ,y ),
0 0 1 1 2 2
xx xx
由题意得:切线EA的方程为: 1 −y y=1,将点E带入得: 1 0 −y y =1,
4 1 4 1 0
x x x x
同理可得: 2 0 −y y =1,易知点A,B都在直线 0 −y y=1上,
4 2 0 4 0
x x
所以直线l的方程为: 0 −y y=1,
4 0
因为直线l过点M(4,0),所以x =1,
0
所以点E恒在定直线L:x=1上.
1−x =λ(x −4),
(2)法一:设N(1,y ),因为AN =λMA,所以 1 1
3 y −y =λy ,
3 1 1
1+4λ
x = ,
1 1+λ
整理得
y = y 3 ,
1 1+λ
1+4λ 2
因为点A(x,y )在双曲线上,所以 1+λ y 2 ,
1 1 −
3
=1
4 1+λ
整理得12λ2−4y2−3=0,
3
同理可得12µ2−4y2−3=0,
3
所以,λ,µ是关于x的方程12x2−4y2−3=0的两个实根,
3
所以λ+µ=0.
法二:由题意知,l的斜率存在,设l的方程:y=k(x−4),
y=k(x−4)
联立 x2 得: ( 1−4k2) x2+32k2x− ( 64k2+4 ) =0,
−y2 =1
4
Δ= ( 32k2)2 +4 ( 1−4k2)( 64k2+4 ) >0
32k2 64k2+4
所以x +x = ,xx = ,
1 2 4k2−1 1 2 4k2−1
答案第12页,共15页 1−x
设N(1,y ),因为AN =λMA,所以1−x =λ(x −4),所以λ= 1 ,
3 1 1 x −4
1
1−x
同理µ= 2 ,
x −4
2
1−x 1−x −2xx +5(x +x )−8
所以λ+µ= 1 + 2 = 1 2 1 2
x −4 x −4 xx −4(x +x )+16
1 2 1 2 1 2
−128k2−8+160k2−32k2+8
= =0.
64k2+4−128k2+64k2−16
x2
(3)设l:x=ty+4,与C: − y2 =1联立得:
4
( t2−4 ) y2+8ty+12=0,
8t 12
y +y =− , y y = ,
1 2 t2−4 1 2 t2−4
因为直线L的方程为x=1,所以P(1,y ),Q(1,y ),
1 2
1 1 1
所以S = AP ⋅ y = x −1⋅ y = ty +3⋅ y ,
1 2 1 2 1 1 2 1 1
1 3
同理S = ty +3⋅ y ,S = y −y ,
2 2 2 2 3 2 1 2
12 12t2 24t2
SS 1 4 y 1 y 2 ⋅t2y 1 y 2 +3t(y 1 +y 2 )+9 t2−4 ⋅⋅ t2−4 − t2−4 +9 1
所以m= 1 2 = = = ,
S 3 2 9 4 (y 1 −y 2 )2 9 − t2 8 − t 4 2 − t2 4 − 8 4 4
1 1
故存在m= ,使得SS = S2.
4 1 2 4 3
19.(1)a = n是D数列,a =2n不是D数列,理由见解析
n n
(2)证明见解析
(3)证明见解析 微信公众号:智慧学库
【详解】(1)a = n是D数列,a =2n不是D数列,理由如下:
n n
当a = n时,a2 =n,a2 =n+1,
n n n+1
答案第13页,共15页
学科网(北京)股份有限公司则a2 −a2 =n+1−n=1,故是D数列;
n+1 n
当a =2n时,a2 =22n,a2 =22n+2,
n n n+1
则a2 −a2 =22n+2−22n =3×22n,故不是D数列;
n+1 n
(2)若{a }是D数列,则a >0且a2 −a2 =d ,
n n n+1 n
此时数列
{ a2}
是以a2为首项,d为公差的等差数列,
n 1
故a2 =a2+(n−1)d,当d <0时,则总存在正整数n,使a2+(n−1)d <0,
n 1 1
与a >0矛盾,故d >0恒成立,a2 −a2 =d >0,
n n+1 n
有a2 =a2+(n−1)d >(n−1)d,a2 =a2+nd >nd,
n 1 n+1 1
即a > (n−1)d ,a > nd ,有a +a > (n−1)d + nd = ( n+ n−1 ) d ,
n n+1 n+1 n
d d d
则b n =a n+1 −a n = a +a < ( n+ n−1 ) d = n+ n−1 ,
n+1 n
由 n+ n−1随n的增大而增大,
d
故总存在正整数n使 <1,即数列{b }中存在小于1的项;
n
n+ n−1
(3)由(2)得a2 =a2+(n−1)d,故a = a2+(n−1)d ,
n 1 n 1
1 1 2
= =
即
a a2+(n−1)d a2+(n−1)d + a2+(n−1)d
n 1 1 1
( )
2 a2+nd − a2+(n−1)d
2 1 1
> =
( )( )
a2+nd + a2+(n−1)d a2+nd + a2+(n−1)d a2+nd − a2+(n−1)d
1 1 1 1 1 1
( )
2 a2+nd − a2+(n−1)d
1 1 ,
=
d
n 1 2( )
则∑ > a2+d − a2 + a2+2d − a2+d ++ a2+nd − a2+(n−1)d
a d 1 1 1 1 1 1
i=1 i
2( )
= a2+nd −a ,由 a2+nd −a 随n的增大而增大,
d 1 1 1 1
2( )
且n→+∞时, a2+nd −a →+∞,
d 1 1
答案第14页,共15页2( )
故对任意的d >0,总存在正整数n使 a2+nd −a >2024,
d 1 1
n 1
即总存在正整数n,使得∑ >2024.
a
i=1 i
答案第15页,共15页
学科网(北京)股份有限公司