文档内容
2025届高三部分重点中学12月联合测评
数学试题参考答案及多维细目表
知必要性成立.
题号
1 2 3 4 5 6 .答案
答案 6 【 】A
C D B D C A 【 解析 】 设等比数列 { a n} 的公比为q , q ≠0, 依题
题号
7 8 9 10 11 意 1 1 1 a 1 即1 1 1
答案 ,a +a +a =14,2= , a +a +aq=
1 2 3 4 2 2 2
A B AD ABC BCD
q
.答案
1 【 】C q
【 解析 】∵ A ={ x |ln( x -1)≤0}={ x |1< x ≤2}, a +a 1 +a 1 q 1 =14,∴2 q +2+q 2 =7,2 q2 -
2 2 2
{ }
B ={ x |0≤2 x -1≤2}= x 1 2 ≤ x ≤ 3 2 , 5 q +2=0, 解得q =2 或q = 1 ,∴ a 1= 1 , a 2=
2 8
{ }
A B x 1 x .
∴ ∪ = ≤ ≤2 1a 1或a 1a 1a 1 S 1
2 ,3= 1= ,2= ,3= ,∴ 3=
.答案 4 2 2 4 8 8
2 【 】D
1 1 7.
解析 由z 4+i可得z (4+i)(1+i) + + =
【 】 = = = 4 2 8
1-i (1-i)(1+i) .答案
æ ö 7 【 】A
3+
2
5i
,
z
=
3-
2
5i
,
故对应的点为
è
ç3
2
,-
5
2
ø
÷
,
位于
【
解析
】
由题知F
(1,0),
直线l的斜率不为
0,
设
第四象限. 直线l的方程为x my A x y
= +1, (1, 1),
.答案 B(x y )
3 【 】B 2,2 ,
解析 8 x 9 增加两个样本点后
【 】∵i∑ i = ×8=9,∴
=1 8
x的平均数为9-1+2 ^ y 9 1
=1;∵ =2× - =2,
10 8 4
∴i∑
8 yi
=2×8=16,∴
增加两个样本点后y的平
=1
均数为16+5+9 ^ b 解得^ b
=3,∴3=3×1+ , =0,
10
新的经验回归方程为^ y x 则当x 时^ y
∴ =3 , =4 , {x my
4 . 【 = 答 12 案 , 】 ∴ D 样本点 (4,10) 的残差为 10-12=-2 . 联立 y2 = =4 x + , 1,整理得y2 -4 my -4=0, 则y 1
解析 y myy .
【 】∵2023 2025 =(2024-1) 2025 =C 0 20252024 2025 + 2=4 ,1 2=-4
-C 1 20252024 2024 ++C 2 2 0 0 2 2 4 52024-C 2 2 0 0 2 2 5 5= ∴
x
1+
x
2=
m
(
y
1+
y
2)+2=4
m2
+2
.
2024(C
0
20252024
2024
-C
1
20252024
2023
+ + ∵
OP→
=
OA→
+
OB→
,∴
四边形OAPB 为平行四
C
2
2
0
0
2
2
4
5-1)+2024-C
2
2
0
0
2
2
5
5,∴
b
=2024-C
2
2
0
0
2
2
5
5=
边形.
2023. 点P的横坐标为 x x m2
.答案 ∵ 3,∴3= 1+ 2=4 +2,
5 【 】C
解析 θ 则a b a b ab 解得m2 1.
【 】∵cos =1, =||||,∴ , =
4
同向 但当a b 时显然不满足a b
, ||-||<0 | - |= AB m2 y y 2 yy
a b 因此充分性不成立. a b a ∴| |= 1+ (1+ 2)-4 1 2 =
||-||, ∵| - |=||
-| b |,∴(| a - b |) 2 =(| a |-| b |) 2 , 即 | a | 2 + 1+ m2 16 m2 -4×(-4)=5 .
b2 a b a2 b2 a b 即a
||-2 =||+||-2||||, 点O到直线AB的距离为 1 25 平
b
=|
a
||
b
|,
从而a
,
b同向
,cos
θ
=1,
由此可
1+
m2 =
5
,∴
数学试题 参考答案 第 页 共 页
1 7对于选项 x y 且z 由糖水原理可
行四边形OAPB的面积为 25 . B,∵ > >0 >0,
5× =25 y z y
5 知 + 故错误
.答案 x z>x, ;
8 【 】B +
【 解析 】 如图 , 取AB中点M , 连接PM , CM. 对于选项 C, 当x <0< y时 , 结论不成立 , 故
由题可知AB ⊥ PM , AB ⊥ CM. 错误 ;
∵ PM ∩ CM = M , PM ⊂ 平面PMC , CM ⊂ 平面 对于选项 D, æ è çx +y 1 ö ø ÷ - æ è çy +x 1 ö ø ÷ = xy y +1 -
PMC AB 平面PMC.
,∴ ⊥
xy æ ö
作PH MC 垂足为H. PH 平面PMC +1 (xy )ç1 1÷ 即x 1 y
⊥ , ∵ ⊂ , x = +1 èy-xø>0, +y> +
AB PH.
∴ ⊥
1 故正确.
又CM AB M CM 平面ABCAB 平面 x,
∩ = , ⊂ , ⊂
ABC PH 平面ABC. .答案
,∴ ⊥ 10 【 】ABC
过点H 作HN BC 垂足为N 连接PN 易知 ì
⊥ , , , ï φ k π
BC PN. ïï0+ =2π+ ,
⊥ 解析 由图可知A í 6
【 】 =2,ïω
PH PB
设小球半径为r ,∴ r=FB= 3 ,∴ PH =3 r. î ï5 12 π + φ =2 k π+π,
2 2
根据 题 意 , V三棱锥PGABC = 1S △ ABC PH = k ∈ Z , 解得ω =2, φ =2 k π+ 6 π , k ∈ Z ,
3
æ ö
fx çx π÷.
1 ( S △ PAB + S △ PAC + S △ PBC + S △ ABC) r , ∴ ()=2sinè2 + 6 ø
3
é ù
∵ S △ PAB = S △ ABC =2, S △ PAC = S △ PBC,∴6=4+ 对于选项 A, 当x ∈ ë ê ê - π , π û ú ú时 ,2 x + π ∈
S S S . 3 6 6
2 △
PAC,∴
△
PAC
= △
PBC
=1 é ù é ù
ê ê π π ú ú fx 在区间 ê ê π π ú ú上单调
由1BC PN 得PN PBC ë- , û,∴ ( ) ë- , û
=1, =1,∴sin∠ = 2 2 3 6
2 递增 故正确
, ;
PN
1 PBN 3. æ ö æ ö
PB= ,∴cos∠ = 对于选项 fç2π÷ ç4π π÷ 3π
2 2 B, è ø=2sinè + ø=2sin
3 3 6 2
PC PB2 CB2 PB CB PBC
∴ = + -2 cos∠ = 为其最小值 x 2π为fx 图象的一
=-2 ,∴ = ( )
. 3
6- 2
条对称轴 故正确
, ;
æ ö æ ö
对于 选 项 f ç11π÷ ç11π π÷
C, è ø =2sin è + ø =
12 6 6
æ ö
点ç11π ÷为fx 图象的一个
2sin2π=0,∴ è ,0ø ( )
12
对称中心 故正确
, ;
é ù
对于选项 当x ê ê π ú ú 时 x π
D, ∈ ë0, û ,2 + ∈
.答案 4 6
9 【 】AD é ù
x ê êπ 2π ú ú 当 x π π即x 时 f x
解析 对于选项 当x 时 2 2 . ë , û, 2 + = =0 , ()min
【 】 A, >0 ,x2 = 6 3 6 6
+1 x 1
+x 当 x π π即x π时 f x
=1, 2 + = = , ()max=2,
6 2 6
x 1 当且仅当x 时 取等号 é ù
∵ +x≥2, =1 , ,∴ 即fx 在区间 ê ê π ú ú上的值域为 故
( ) ë0, û [1,2],
x 4
2 2 故正确. 错误.
x2 = ≤1,
+1 x 1
+x .答案
11 【 】BCD
数学试题 参考答案 第 页 共 页
2 7解析 对于选项 沿C B A A B 的概率为 . .
【 】 A, 1→ 1→ 1→ → → (96,100) 1-2×005=09,
C C 等路线即可 故错误 即 件产品的质量指标位于区间 的概
→ 1 , ; 1 (96,100)
对于选项 若存在重复路线 两次移动回到点 率为 . Y B . 故DY
B, , 09,∴ ~ (500,09), ( )=500×
C 可以第一次移动到达点A B C 第三次 . . .
1 1, 1, , 09×01=45
移动再从这些移动方式中选 , 共有 9 种走法 , 另 14 . 【 答案 】[e -e ,1)
外 能到 可 达 以 点 先 A 移动 B 两次 C 再 每 原 个 路 点 返 在 回 第 , 第 二 一 次 次 移 移 动 动 时 可 都 【 解析 】 f ( x )= ax -1 -log a( x -1)= a a x -
1,1, ,
有两种移动方式 故有 种方式 x
, 6 ; ln(-1) 1 ax a a x
a =a a[ ln - ln(-1)],
若不存在重复路线 经过点C由四条棱组成的 ln ln
,
闭合回路只有C 1 A 1 ACC 1 和C 1 B 1 BCC 1 两种 , 记h ( x )= ax ln a - a ln( x -1), f ( x ) 在定义域
每条路都有两种经过方式 共有 种方式 概
上单调 可得hx 必为单调函数.
, ()
, 4 ,∴
率为 æ ç1 ö ÷ 4 19 故正确 若h ( x ) 单调递增 , 则h′ ( x )= ax (ln a ) 2 -
è ø 19= , ;
a
3 81 恒成立 即x ax -1 1
对于选项 列举法 C A A B B x ≥0 , (-1) ≥ a2 ,
C, :1→ 1→ → → 1→ -1 (ln )
C C A A B C C C A B
1,1→ 1→ → → → 1,1→ 1→ 1→ tat 1 .又函数Gt tat在t 时值
∴ ≥ a2 ()= →0
B C C C B A A C C C C (ln )
→ → 1,1→ 1→ 1→ → → 1,1→
趋近于 不满足.
A B B C 故共有 条不同笔记 故 0,
→ → → 1→ 1, 5 ,
正确 若h ( x ) 单调递减 , 则h′ ( x )= ax (ln a ) 2 -
;
对于选项 先考虑重复路线 a
D, :
x ≤0
恒成立
,
即
(
x
-1)
ax -1
≤
1
a2 ,
即
前两条路线重复 第一次移动到达点A B C -1 (ln )
, 1,1,
共 条路径 后两条路径重复 即第一次移动到 tat 1
3 ; ( ≤ a2 ,
点A 同理有 条路径 其中C A C
(ln )
1) 3 , 1→ 1→ 1→
A 1 重复 , 故共只有 5 条路径 ; ∴( tat )max≤ (ln 1 a ) 2 , 设G ( t )= tat , G′ ( t )=(1
再考虑不重复路径 只有C C A A 条
: 1→ → → 1,1
t aat 则t 1
路径 三次移动后到达点A有 条路径.记事 +ln ) =0, =- a,
,∴ 6 ln
件A 从点C 出发 三次移动后到达点A 事 当a 时t 不成立
1: 1 , 1; >1 ,<0 ;
件C 从点C 出发 三次移动时经过点C 故
: 1 , , 当 a 时t 1 Gt 在区间
æ ö æ ö 0< <1 ,=- a>0,∴ ()
3 3 ln
PA ç1÷ PAC ç1÷
(1)=è ø 6, (1 )=è ø 2, æ ö
3 3 ç 1 ÷ 上 单 调 递 增 在 区 间
PAC
è0,- aø ,
故PCA (1 ) 1 故正确.也可以 ln
(| 1)=PA = , ( æ ö
(1) 3 ç 1 ÷上单调递减
直接列举路径来判断 è- a,+∞ø ,
) ln
.答案
12 【
解析
】8
根据点F到其中一条渐近线的距离为 ∴- ln
1
a
a-ln 1a
≤ (ln
1
a ) 2 ,
即a-ln 1a
≤- ln
1
a,
【 】
æ ö æ ö
2, 可得b =2, 且满足α + β =π .又α = 1β ,∴ β = ∴ è ç - ln 1 aø ÷ ln a ≤ln è ç - ln 1 aø ÷ , 即 -1≤
5
æ ö
π b β 3 故a c 焦 lnè ç - 1 aø ÷ , 解得 e -e ≤ a <1 .
,∴a=tan = , =23,∴ =4,∴ ln
6 3
距为 c . æ ç A Aö ÷ 2
2 =8 èsin +cos ø
.答案 .解 由二倍角公式得 2 2
13 【 】45 15 :(1) A A =
解析 由正态分布的性质得质量指标在区间 cos 2 -sin 2
【 】 2 2
数学试题 参考答案 第 页 共 页
3 7æ B Bö 2 又PA 平面ABCDBD 平面ABCD
ç ÷ ⊥ , ⊂ ,
èsin +cos ø
2 2 分 PA BD.
B B , 2 ∴ ⊥
2 2 又ACPA 平面PACAC PA A
cos -sin , ⊂ , ∩ = ,
2 2
BD 平面PAC.
A A B B
∴ ⊥
sin +cos sin +cos 又BD 平面PBD 平面PAC 平面PBD.
2 2 2 2 ⊂ ,∴ ⊥
∴ A A= B B,
分
cos -sin cos -sin 7
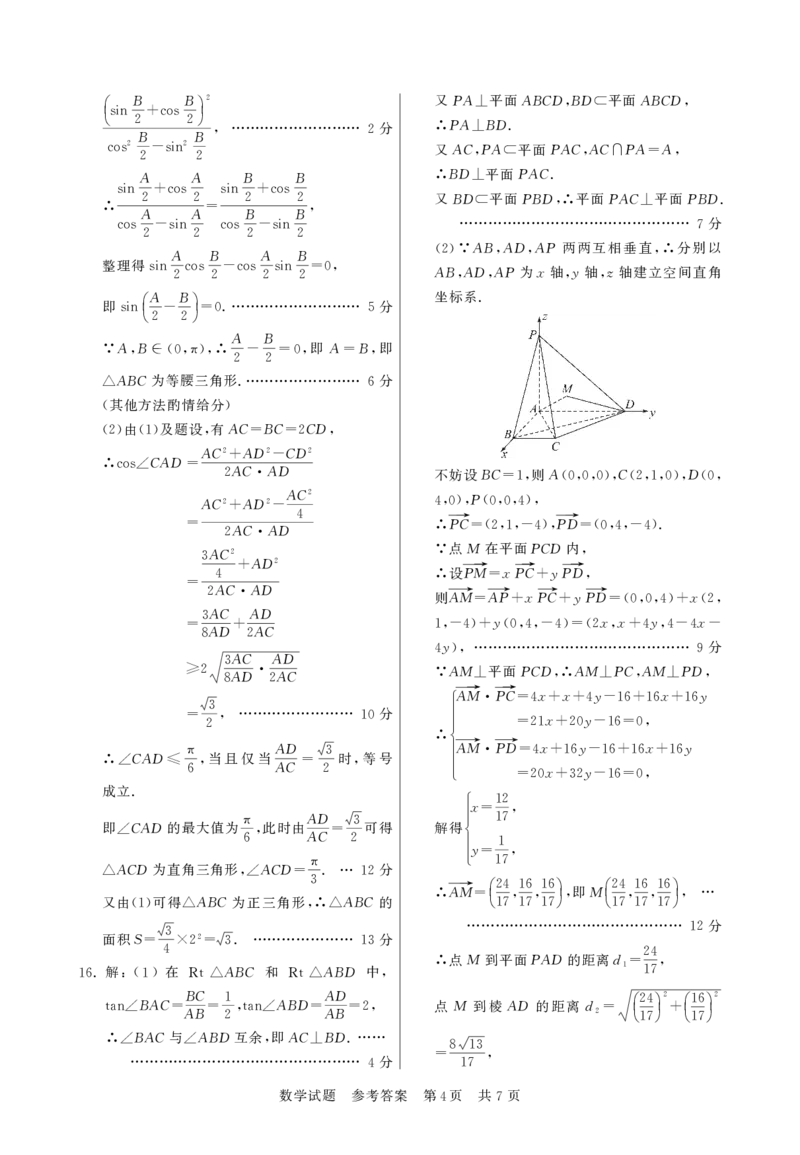
2 2 2 2 AB AD AP 两两互相垂直 分别以
A B A B (2)∵ , , ,∴
整理得
sin cos -cos sin =0, ABADAP为x轴y轴z轴建立空间直角
2 2 2 2 , , , ,
æA Bö 坐标系.
即 ç ÷ . 分
sinè - ø=0 5
2 2
A B
A B 即A B 即
∵ , ∈(0,π),∴ - =0, = ,
2 2
ABC为等腰三角形. 分
△ 6
其他方法酌情给分
( )
由 及题设 有AC BC CD
(2) (1) , = =2 ,
AC2 AD2 CD2
CAD + -
∴cos∠ = 2 AC AD 不妨设BC =1, 则A (0,0,0), C (2,1,0), D (0,
AC2
P
AC2 AD2 4,0), (0,0,4),
+ -
4 PC→ PD→ .
= AC AD ∴ =(2,1,-4), =(0,4,-4)
2
点M 在平面PCD内
AC2 ∵ ,
3 AD2
+ 设PM→ xPC→ yPD→
4 ∴ = + ,
= AC AD
2 则AM→ AP→ xPC→ yPD→ x
= + + =(0,0,4)+ (2,
AC AD
3 y xx y x
= AD+ AC 1,-4)+ (0,4,-4)=(2 , +4 ,4-4 -
8 2 y 分
AC AD 4 ), 9
3 AM 平面PCD AM PCAM PD
≥2 AD AC ∵ ⊥ ,∴ ⊥ , ⊥ ,
8 2
ì ïAM→ PC→ x x y x y
=4 + +4 -16+16 +16
3 分 ï
= , 10 ï x y
2 í =21 +20 -16=0,
∴ï
AD AM→ PD→ x y x y
CAD π 当且仅当 3时 等号 ï =4 +16 -16+16 +16
∴∠ ≤ 6 , AC= 2 , î ï =20 x +32 y -16=0,
成立.
ì
ï
x 12
AD ïï = ,
即 CAD的最大值为π 此时由 3可得 解得í 17
∠ , AC= ï
6 2 ïy 1
î = ,
ACD为直角三角形 ACD π. 分 17
△ ,∠ = 12 æ ö æ ö
3 AM→ ç241616÷ 即Mç241616÷
又由 可得 ABC为正三角形 ABC的 ∴ =è , , ø, è , , ø,
(1) △ ,∴△ 171717 171717
分
面积S 3 2 . 分 12
= ×2= 3 13
4 点M 到平面PAD的距离d 24
.解 在 ABC 和 ABD 中 ∴ 1= ,
16 :(1) Rt△ Rt△ , 17
BC AD æ ö æ ö
BAC 1 ABD 点M 到棱AD 的距离d ç24÷ 2 ç16÷ 2
tan∠ =AB= ,tan∠ =AB=2, 2= è ø +è ø
2 17 17
BAC与 ABD互余 即AC BD.
∴∠ ∠ , ⊥
8 13
分 = ,
4 17
数学试题 参考答案 第 页 共 页
4 7d é ù
设二面角MGADGP大小为θ 则 θ 1 g′x gx f′x 在区间ê ê 3π ú ú上单
, sin =d = ∴ ()>0,()= () ëπ, û
2 2
调递增.
24 3 13
= , æ ö
8 13 13 g gç3π÷ 存在x
(π)=-1<0, è ø=π>0,∴ 0∈
2
∴cos
θ
= 1-sin
2θ
=
2
13
13
, æ ç 3π ö ÷ 使得gx 分
èπ, ø, (0)=0, 11
2
即二面角MGADGP的余弦值为2 13. 且x x 时 gx f′x 即此时
13
∈(π,0) , ()= ()<0,
分 fx 在区间 x 上单调递减
15 () (π,0) ;
æ ö æ ö
.解 f′ x x çx π÷ x 且 x çx 3π÷ 时 gx f′x 即 此 时
17 :(1) ( )=cos - è - øsin , ∈ è 0, ø , ()= ()>0,
2 2
æ ö æ ö
f′çπ÷ . 分 fx 在区间çx 3π÷上单调递增. 分
è ø=0 2 () è 0, ø 13
2 2
æ ö
当
0<
x
<
π时
,cos
x
>0,è
çx
-
π
ø
÷
sin
x
<0,
从
∴
由f
(π)=-
π
+1<0,
得f
(
x
0)<0,
2 2 2
而f′
(
x
)=cos
x
-
æ
è
çx
-
π ö
ø
÷
sin
x
>0,
即函数f ( x ) 在区间 (π, x 0) 上无零点 ;
2 æ ö
é ù 而由fx fç3π÷
即此时函数fx 在区间ê ê π ú ú上单调递增 (0)<0, è ø=1>0,
() ë0, û ; 2
2 æ ö
分 即函数fx 在区间çx 3π÷上有唯一的零点.
4 () è 0, ø
2
æ ö
当π < x ≤π 时 ,cos x <0,è çx - π ø ÷ sin x ≥0, 函数fx 在区间 é ê êπ 3π ù ú ú上有 个零点.
2 2 ∴ () ë , û 2
2 2
æ ö
从而f′x x çx π÷ x 分
()=cos -è - øsin <0, 15
2 .解 由题意知抛物线的焦点P到两定点A
é ù 18 :(1) ,
即此时函数f ( x ) 在区间 ë ê êπ ,πû ú ú上单调递减. B的距离之和等于点A
,
B到抛物线的准线的
2
é ù 距离之和 等于AB的中点O到准线的距离的
综上所述 函数fx 在区间 ê ê π ú ú上单调 ,
∴ , ( ) ë0, 2 û 2 倍 , 即等于圆x2 + y2 =9 的半径的 2 倍 ,
é ù
递增 , 在区间 ë ê êπ ,πû ú ú上单调递减. 7 分 ∴| PA |+| PB |=6>| AB |=2,∴ 点P在以
2 AB为焦点的椭圆E上 分
æ ö , , 3
(2) f è çπ ø ÷ =1>0, 又f (π)=- π +1<0, 且函 设椭圆E的标准方程为 x2 y2 a b
2 2 a2+b2=1(> >0),
é ù
数f ( x ) 在区间 ë ê ê
2
π ,πû ú ú上单调递减 , 则
2
a
=6,2
c
=2,∴
a
=3,
c
=1,∴
b2
=
a2
-
c2
é ù
函数fx 在区间ê êπ ú ú上存在唯一的零点. =8,
∴ () ë
2
,πû
曲线E的标准方程为
x2 y2
. 分
分 ∴ + =1 8
9 9 8
é ù 设直线MNx my m
当x ê ê 3π ú ú时 记gx f′x x (2) := +2( ≠0),
∈ ëπ, 2 û , ()= ()=cos - 由 {x = my +2,
æ ö
è
çx
-
π
ø
÷
sin
x
, 8
x2
+9
y2
=72,
2
m2 y2 my .
æ ö ∴(8 +9) +32 -40=0
从而g′
(
x
)=-2sin
x
-è
çx
-
π
ø
÷
cos
x
, 设 M x y N x y 则y y
2 (1, 1), (2, 2), 1 + 2 =
æ ö m
且此时 x çx π÷ x -32 yy -40
sin <0,è - øcos <0, m2 ,1 2= m2 ,
2 8 +9 8 +9
数学试题 参考答案 第 页 共 页
5 7æx y ö y 首先 若对数列S a a a a a 依次做
CM 的中点坐标为ç 1-3 1÷ k 1 (2) , 0:1,2,3,4,5
è 2 , 2 ø,CM =x 1+3 , A i +1, A i +2,, A 5( i ∈{1,2,3,4}) 变换 , 得到
分
9 的数列a i 加 1, a i +1 减 1, 其余项不变 ;
CM 的垂直平分线的斜率为 - x y 1+3. 10 分 若对数列中S 0: a 1, a 2, a 3, a 4, a 5 依次做A i,
1 A A i 变换 得到的数列
x
i -1,,1(∈{1,2,3,4}) ,
CM 的垂直平分线方程为y 1+3 中a 减 a 加 其余项不变. 分
∴ =- y i 1,i +1 1, 7
1 可以通过若干次变换使得相邻两数一个加
æ x ö y my x2 ∴
è çx - 1
2
-3 ø ÷ +
2
1 , 即y =- y 1
1
+5x +
2
1 y -
1
9 1, 另一个减 1,
可以通过若干次变换使得第一项变为 第
y ∴ 0,
1
+ , 二项变为a a.
2 1+ 2
x2 y2 x2 同样的可以通过若干次变换分别使得a a
由 1 1 得 1-9 9y 2,3,
+ =1 y =- 1,
9 8 2 1 16 a 均变为 此时即为 . 分
4 0, 0,0,0,0,0 10
my
CM 的垂直平分线方程为y 1+5x 记此时的变换 为B 变换 为B .
∴ =- y - (3) ① 1, ③ 10
1 首先 记T a a a a a T a
, 1= 1+ 3+ 5+ 7+ 9, 2= 2+
1
1
6
y 1 . 11 分 a 4+ a 6+ a 8+ a 10,
每次变换使得T 的值加 或减 或不变 故可
同理CN的垂直平分线方程为y my 2+5x 1 2 2 ,
=- y 以经过若干次变换使得T 此时T
2 1=0, 2=0;
其次 对任意数列S a a a 依次做
1y . 分 , 0:1,2,,10
- 16 2 13 A j -1, A j, A j, A j +1 变换 , 其中j ∈{3,4,,8},
设点Qx y
(0,0), 得到的数列中a
j
减
2,
a
j -2,
a
j +2
均加
1,
其余项
my
则y 1, y 2 是方程y 0=- y +5x 0- 1y , 不变 , 记此变换为B j,
16 依次做A A A 变换 得到的数列中a 减
即y2 mx y y x 的两根 8, 9, 10 , 9
+(16 0+16 0)+80 0=0 , a 加 其余项不变 记此变换为B
ì ï m 1,7 1, , 9,
í ïï y 1+ y 2=-16 mx 0-16 y 0= 8 - m 3 2 2 +9 , 两 式 此时B 1, B 3, B 5, B 7, B 9 只变换a 1, a 3, a 5, a 7,
∴ ï a 且对a a a a a 规则同第 问 且
ïyy x -40
9, 1,3,5,7,9 (2) ,
î 1 2=80 0= m2 , T 分
8 +9 1=0, 15
mx y m y 由 知可以对S 做若干次变换 得到的数
相除得- 0- 0 4 0 m. ∴ (2) 0 ,
x = ,∴x =-5
5 0 5 0 列中a a a a a .
1= 3= 5= 7= 9=0
分
16 同理可以再对S 做若干次变换 得到的数列中
0 ,
k k m 1 a a a a a 则此时得到数列
∴ OQ MN =-5 m=-5, 2= 4= 6= 8= 10=0,
. 分
即直线OQ与MN的斜率之积为定值 . 0,0,,0 17
-5 个
10
分 其他方法酌情给分
17 ( )
其他方法酌情给分
( )
.解 对数列S 依次做A A A 变换即可.
19 :(1) 0 3,4,5
分
4
数学试题 参考答案 第 页 共 页
6 7多维细目表
学科素养 预估难度
题型 题号 分值 必备知识 数学 逻辑 数学 直观 数学 数据
易 中 难
抽象 推理 建模 想象 运算 分析
选择题 集合与简易逻辑
1 5 √ √
选择题 复数
2 5 √ √
选择题 统计与概率
3 5 √ √
选择题 二项式定理
4 5 √ √ √
选择题 平面向量
5 5 √ √ √
选择题 等比数列
6 5 √ √ √
选择题 抛物线方程及其性质
7 5 √ √
选择题 立体几何
8 5 √ √ √
选择题 不等式的性质
9 6 √ √ √
选择题 三角函数的图象及其性质
10 6 √ √
选择题 排列组合与概率
11 6 √ √ √
填空题 双曲线方程及其性质
12 5 √ √ √
填空题 概率分布
13 5 √ √ √
填空题 导数及其应用
14 5 √ √ √
解答题 解三角形
15 13 √ √ √
解答题 立体几何
16 15 √ √ √
解答题 导数及其应用
17 15 √ √ √ √
解答题 椭圆方程及其性质
18 17 √ √ √
解答题 数列与新定义综合
19 17 √ √ √ √
数学试题 参考答案 第 页 共 页
7 7