文档内容
专题 1.2 空间向量的数量积运算【五大题型】
【人教A版(2019)】
【题型1 空间向量数量积的计算】..........................................................................................................................2
【题型2 空间向量的夹角及其应用】......................................................................................................................4
【题型3 利用空间向量的数量积求模】..................................................................................................................6
【题型4 向量垂直的应用】......................................................................................................................................8
【题型5 投影向量的求解】....................................................................................................................................11
【知识点1 空间向量的夹角与数量积】
1.空间向量的夹角
(1)定义:已知两个非零向量a,b,在空间任取一点O,作OA=a,OB=b,则∠AOB叫做向量a,b
的夹角,记作〈a,b〉.
(2)范围:0≤〈a,b〉≤π.
特别地,当〈a,b〉=时,a⊥b.
2.空间向量的数量积
已知两个非零向量a,b,则|a||b|cos 〈a,b〉叫做a,b的数量积,记作
a·b.
定义
即a·b=|a||b|cos〈a,b〉.
规定:零向量与任何向量的数量积都为0.
①a⊥b a·b=0
性质
②a·a=a2=|a|2
⇔
①(λa)·b=λ(a·b),λ∈R.
运算律 ②a·b=b·a(交换律).
③a·(b+c)=a·b+a·c(分配律).
3.空间向量夹角的计算
求两个向量的夹角:利用公式 = 求 ,进而确定 .
学科网(北京)股份有限公司4.空间向量数量积的计算
求空间向量数量积的步骤:
(1)将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入 求解.
【题型1 空间向量数量积的计算】
【例1】(2023秋·高一单元测试)在空间四边形ABCD中,⃗AB·⃗CD+⃗AC·⃗DB+⃗AD·⃗BC等于( )
A.−1 B.0 C.1 D.不确定
【解题思路】令⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c,利用空间向量的数量积运算律求解.
【解答过程】令⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c,
则⃗AB·⃗CD+⃗AC·⃗DB+⃗AD·⃗BC,
,
=⃗a·(⃗c−⃗b)+⃗b·(⃗a−⃗c)+⃗c·(⃗b−⃗a)
=⃗a·⃗c−⃗a·⃗b+⃗b·⃗a−⃗b·⃗c+⃗c·⃗b−⃗c·⃗a=0.
故选:B.
【变式1-1】(2023春·江苏盐城·高二校联考期中)如图,各棱长都为2的四面体ABCD中 ⃗CE = ⃗ED,
⃗AF =2 ⃗FD,则向量⃗BE⋅⃗CF=( )
1 1 1 1
A.− B. C.− D.
3 3 2 2
1 1 2
【解题思路】由向量的运算可得⃗BE= (⃗BC+⃗BD),⃗CF= ⃗BA−⃗BC+ ⃗BD,由向量数量积的定义即可
2 3 3
得到答案.
π
【解答过程】由题得⃗BA,⃗BC夹角,⃗BD,⃗BC夹角,⃗BD,⃗BA夹角均为 ,
3
∵⃗CE=⃗ED,⃗AF=2⃗FD,
1 2
∴⃗BE= (⃗BC+⃗BD),⃗AF= ⃗AD,
2 3
∴⃗CF=⃗BF−⃗BC=⃗BA+⃗AF−⃗BC
学科网(北京)股份有限公司2 2 1 2
=⃗BA+ ⃗AD−⃗BC=⃗BA+ (⃗BD−⃗BA)−⃗BC= ⃗BA−⃗BC+ ⃗BD,
3 3 3 3
∴⃗BE⋅⃗CF= 1 (⃗BC+⃗BD)⋅ (1 ⃗BA−⃗BC+ 2 ⃗BD )
2 3 3
1 1 1 1 1
= ⃗BA⋅⃗BC− ⃗BC2− ⃗BC⋅⃗BD+ ⃗BA⋅⃗BD+ ⃗BD2
6 2 6 6 3
1 1 1 1 1 1 1 1 1
= ×2×2× − ×22− ×2×2× + ×2×2× + ×22=−
6 2 2 6 2 6 2 3 3
故选:A.
【变式1-2】(2023春·陕西西安·高一校考期末)在正三棱锥P−ABC中,O是△ABC的中心,
,则 等于( )
PA=AB=2 ⃗PO⋅(⃗PA+⃗PB)
10 2√6 8√2 16
A. B. C. D.
9 3 3 3
【解题思路】将⃗PA转化为⃗PO+⃗OA,⃗PB转化为⃗PO+⃗OB,由三棱锥是正三棱锥可知PO⊥AO,
PO⊥BO,即可将⃗PO⋅⃗PA转化为|⃗PO|2,⃗PO⋅⃗PB转化为|⃗PO|2,结合勾股定理即可求解.
【解答过程】∵P−ABC为正三棱椎,O为△ABC的中心,
∴PO⊥平面ABC,AO、BO⊂平面ABC,
∴PO⊥AO,PO⊥BO,
△ABC是等边三角形,
1 |AB| 2√3 1 |AB| 2√3
∴⃗PO⋅⃗OA=0,|AO|= ⋅ = ,⃗PO⋅⃗OB=0,|BO|= ⋅ = ,
2 sin60∘ 3 2 sin60∘ 3
故⃗PO⋅⃗PA=⃗PO⋅(⃗PO+⃗OA)=|⃗PO| 2 =|PA| 2 −|OA| 2=4− 4 = 8 ,
3 3
⃗PO⋅⃗PB=⃗PO⋅(⃗PO+⃗OB)=|⃗PO| 2 =|PB2|−|OB| 2=4− 4 = 8 ,
3 3
16
则⃗PO⋅(⃗PA+⃗PB)=⃗PO⋅⃗PA+⃗PO⋅⃗PB= .
3
故选:D.
学科网(北京)股份有限公司【变式1-3】(2023秋·山东菏泽·高二统考期末)在棱长为2的正方体ABCD−A B C D 中,EF是正方
1 1 1 1
体ABCD−A B C D 外接球的直径,点P是正方体ABCD−A B C D 表面上的一点,则⃗PE⋅⃗PF的
1 1 1 1 1 1 1 1
取值范围是( )
A.[−2,0] B.[−1,0] C.[0,1] D.[0,2]
【解题思路】求出正方体ABCD−A B C D 的外接球O的半径R,可得出⃗PE⋅⃗PF=PO2−3,求出OP
1 1 1 1
的取值范围,进而可求得⃗PE⋅⃗PF的取值范围.
【解答过程】设正方体ABCD−A B C D 的外接球的球心为O,设球O的半径为R,
1 1 1 1
则2R=2√3,可得R=√3,所以,OE=OF=√3,
2 2
⃗PE⋅⃗PF=(⃗PO+⃗OE)⋅(⃗PO+⃗OF)=(⃗PO+⃗OE)⋅(⃗PO−⃗OE)=|⃗PO| −|⃗OE|
=PO2−3,
当点OP与正方体ABCD−A B C D 的侧面或底面垂直时,OP的长取最小值,即OP =1,
1 1 1 1 min
当点 与正方体 的顶点重合时, 的长取最大值,即 ,
P ABCD−A B C D OP OP =√3
1 1 1 1 max
所以,1≤OP≤√3,所以,⃗PE⋅⃗PF=PO2−3∈[−2,0].
故选:A.
【题型2 空间向量的夹角及其应用】
【例2】(2023春·高二课时练习)若非零向量 , 满足 , ,则 与 的夹角为
⃑a ⃑b |⃑a|=|⃑b| (2⃑a−⃑b)⋅⃑b=0 ⃑a ⃑b
( )
A.30° B.60° C.120° D.150°
1
【解题思路】设 ⃑a与⃑b的夹角为θ,则由(2⃑a−⃑b)⋅⃑b=0,|⃑a|=|⃑b|,可得cosθ= ,从而可求得 ⃑a与⃑b的夹角
2
【解答过程】设⃑a与⃑b的夹角为θ,
因为(2⃑a−⃑b)⋅⃑b=0,所以2⃑a⋅⃑b=⃑b2,
学科网(北京)股份有限公司所以 ,
2
2|⃑a||⃑b|cosθ=|⃑b|
因为非零向量 , 满足 ,
⃑a ⃑b |⃑a|=|⃑b|
1
所以cosθ= ,
2
π
因为θ∈[0,π],所以θ= ,即θ=60°,
3
故选:B.
【变式2-1】(2023·江苏·高二专题练习)已知空间向量 满足 , ,则
⃑a,⃑b,⃑c ⃑a+⃑b+⃑c=0⃑ |⃑a|=2,|⃑b|=3,|⃑c|=4
⃑a与⃑b的夹角为( )
A.30° B.45°
C.60° D.以上都不对
【解题思路】设⃑a与⃑b的夹角为θ,由 ⃑a+⃑b+⃑c=0⃑,得 ⃑a+⃑b=−⃑c,两边平方化简可得答案
【解答过程】设⃑a与⃑b的夹角为θ,
由 ⃑a+⃑b+⃑c=0⃑,得 ⃑a+⃑b=−⃑c,
两边平方,得⃑a2+2⃑a⋅⃑b+⃑b2=⃑c2,
因为 ,
|⃑a|=2,|⃑b|=3,|⃑c|=4
1
所以4+2×2×3cosθ+9=16,解得cosθ= ,
4
故选:D.
π
【变式2-2】(2023春·高二课时练习)空间四边形OABC中,OB=OC,∠AOB=∠AOC= ,则
3
cos⟨⃑OA,⃑BC⟩的值是( )
1 √2 1
A. B. C.− D.0
2 2 2
【解题思路】利用OB=OC,以及⃑OA⋅⃑BC的数量积的定义化简cos⟨⃑OA,⃑BC⟩的值,
【解答过程】解:∵OB=OC,
所以⃑OA⋅⃑BC=⃑OA⋅(⃑OC−⃑OB)=⃑OA⋅⃑OC−⃑OA⋅⃑OB
π π 1
=|⃑OA|⋅|⃑OC|cos −|⃑OA|⋅|⃑OB|cos = |⃑OA|(|⃑OC|−|⃑OB|)=0
3 3 2
所以cos⟨⃑OA,⃑BC⟩=0,
学科网(北京)股份有限公司故选:D.
【变式2-3】(2023春·高二课时练习)已知⃑e ,⃑e 是夹角为60°的两个单位向量,则⃑a=⃑e +⃑e 与
1 2 1 2
的夹角为( )
⃑b=⃑e −2⃑e
1 2
A.60° B.120°
C.30° D.90°
【解题思路】先求数量积,再求向量的模,然后根据向量夹角公式即可求得.
⃑ ⃑ ⃑ ⃑ ⃑ ⃑ ⃑ ⃑ ⃑ ⃑ ⃑ |⃑ | 1 3
【解答过程】a⋅b=(e +e )⋅(e −2e )=e 2−e ⋅e −2e 2=1−|e | e × −2=− ,
1 2 1 2 1 1 2 2 1 2 2 2
|⃑a|=√ ⃑a2=√(⃑e +⃑e ) 2=√ ⃑e 2+2⃑e ⋅⃑e +⃑e 2=√1+1+1=√3
1 2 1 1 2 2
|⃑b|=√⃑b2=√(⃑e −2⃑e ) 2=√ ⃑e 2−4⃑e ⋅⃑e +4⃑e 2=√1−2+4=√3
1 2 1 1 2 2
3
−
所以 ⃑a⋅⃑b 2 1.
cos⟨⃑a,⃑b⟩= = =−
|⃑a||⃑b| 3 2
所以⟨⃑a,⃑b⟩=120°.
故选:B.
【题型3 利用空间向量的数量积求模】
【例3】(2023春·福建宁德·高二校联考期中)已知单位向量 , , 中, , ,
⃗a ⃗b ⃗c ⃗a⊥⃗b ⟨⃗a,⃗c⟩=⟨⃗b,⃗c⟩=60°
则 ( )
|⃗a−⃗b+2⃗c|=
A.√5 B.5 C.6 D.√6
【解题思路】根据题意,由空间向量的模长公式,代入计算,即可得到结果.
【解答过程】因为 , ,且 , , 为单位向量,
⃗a⊥⃗b ⟨⃗a,⃗c⟩=⟨⃗b,⃗c⟩=60° ⃗a ⃗b ⃗c
则 |⃗a−⃗b+2⃗c|=√(⃗a−⃗b+2⃗c) 2 = √ |⃗a| 2+|⃗b| 2 +4|⃗c| 2 −2⃗a⋅⃗b+4⃗a⋅⃗c−4⃗b⋅⃗c
√ 1 1
= 1+1+4−0+4×1×1× −4×1×1× =√6.
2 2
故选:D.
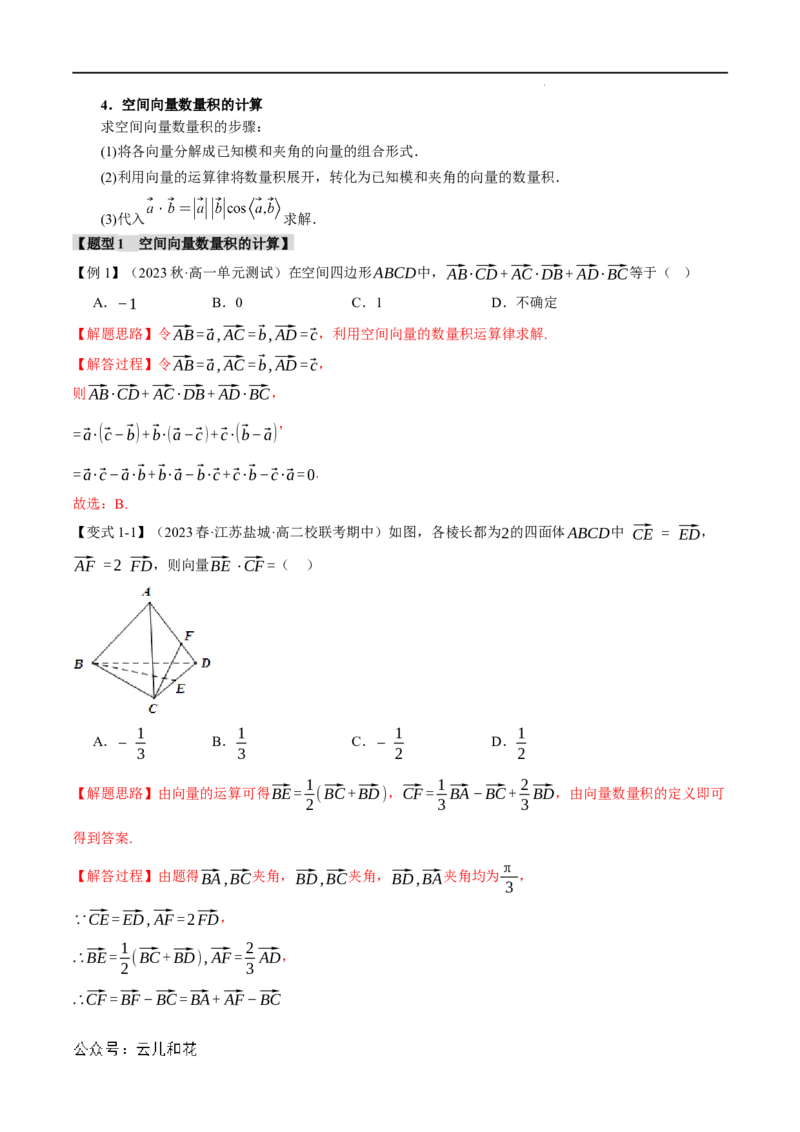
【变式3-1】(2023·江苏·高二专题练习)已知在平行六面体ABCD−A B C D 中,向量⃗AB,⃗AD,
1 1 1 1
学科网(北京)股份有限公司两两的夹角均为 ,且 , , ,则 ( )
⃗A A 60° |⃗AB|=1 |⃗AD|=2 |⃗A A |=3 |⃗AC |=
1 1 1
A.5 B.6 C.4 D.8
【解题思路】利用向量的数量积公式即可求解.
【解答过程】如图,平行六面体ABCD−A B C D 中,
1 1 1 1
向量 、 、 两两的夹角均为 ,
⃗AB ⃗AD ⃗A A 60∘
1
且 , , ,
|⃗AB|=1 |⃗AD|=2 |⃗A A |=3
1
∴⃗AC =⃗AB+⃗BC+⃗CC
1 1
∴ ⃗AC 2=(⃗AB+⃗BC+⃗CC ) 2
1 1
=⃗AB2+⃗BC2+⃗CC 2+2⃗AB·⃗BC+2⃗AB·⃗CC +2⃗BC·⃗CC
1 1 1
=1+4+9+2×1×2×cos60∘+2×1×3×cos60∘+2×2×3×cos60∘
=25.
,
∴|⃗AC |=5
1
故选:A.
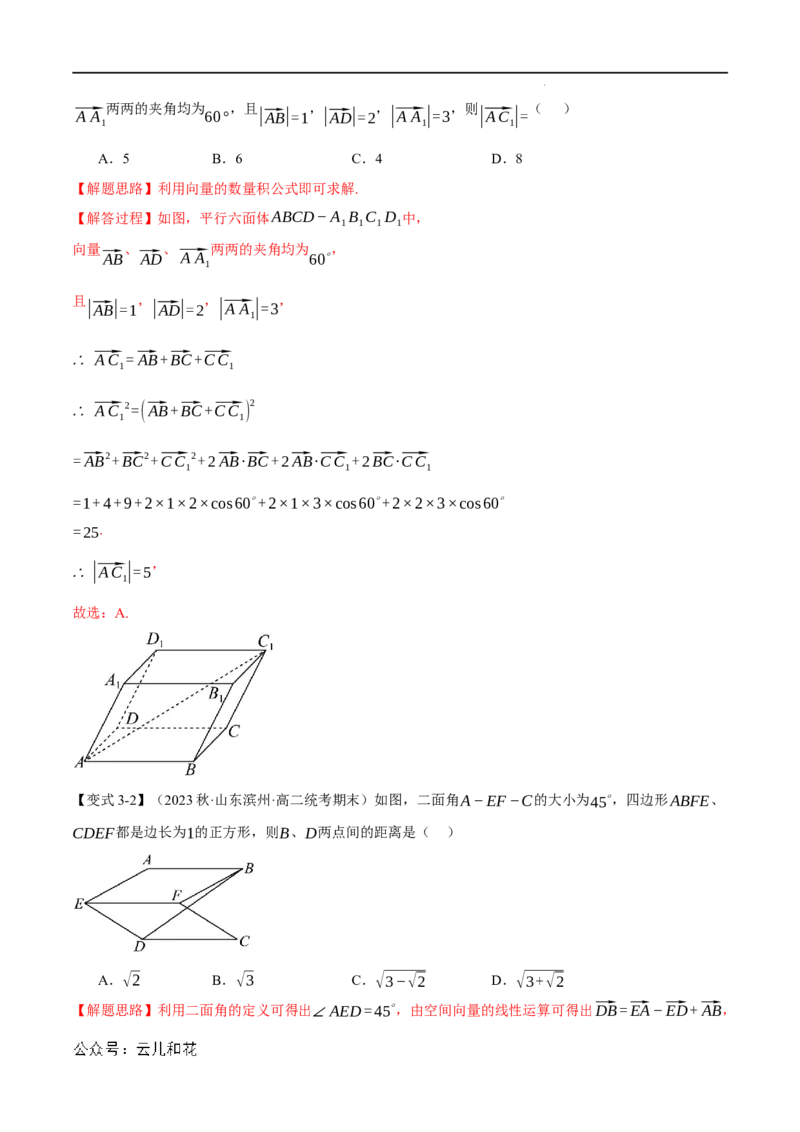
【变式3-2】(2023秋·山东滨州·高二统考期末)如图,二面角A−EF−C的大小为45∘,四边形ABFE、
CDEF都是边长为1的正方形,则B、D两点间的距离是( )
A.√2 B.√3 C.√3−√2 D.√3+√2
【解题思路】利用二面角的定义可得出∠AED=45∘,由空间向量的线性运算可得出⃗DB=⃗EA−⃗ED+⃗AB,
学科网(北京)股份有限公司利用空间向量数量积的运算性质可求得 ,即为所求.
|⃗DB|
【解答过程】因为四边形ABFE、CDEF都是边长为1的正方形,则AE⊥EF,DE⊥EF,
又因为二面角 的大小为 ,即 ,则 ,
A−EF−C 45∘ ∠AED=45∘ ⟨⃗EA,⃗ED⟩=45∘
因为⃗DB=⃗DE+⃗EA+⃗AB=⃗EA−⃗ED+⃗AB,由图易知⃗AB⊥⃗EA,⃗AB⊥⃗ED,
所以,
|⃗DB|=√(⃗EA−⃗ED+⃗AB) 2 =√⃗EA2+⃗ED2+⃗AB2−2⃗EA⋅⃗ED+2⃗EA⋅⃗AB−2⃗ED⋅⃗AB
.
=√1+1+1−2×1×1×cos45∘+0−0=√3−√2
故选:C.
【变式3-3】(2023春·江苏南京·高二校考阶段练习)如图,三棱锥O−ABC各棱的棱长是1,点D是棱
AB的中点,点E在棱OC上,且⃗OE=λ⃗OC,则DE的最小值为( )
1 √2 √3
A. B. C. D.1
2 2 2
【解题思路】首先在△DOC中利用余弦定理求出cos∠DOE,然后由空间向量的运算法则可得
|⃗DE| 2 =|⃗OE−⃗OD| 2,变形可得|⃗DE| 2 =λ2−λ+ 3 ,由二次函数的知识可得答案.
4
√3
【解答过程】根据题意,在△DOC中, OD=CD= ,OC=1,
2
3 3
1+ −
4 4 √3
所以cos∠DOE= =
√3 3
2×1×
2
√3 √3 3 1 2 1
所以|⃗DE| 2 =|⃗OE−⃗OD| 2 =|⃗OE| 2 −2⃗OE⋅⃗OD+|OD| 2=λ2−2×λ× × + =(λ− ) +
2 3 4 2 2
1 1
则λ= 时,|⃗DE| 2取得最小值 ,
2 2
学科网(北京)股份有限公司√2
则|⃗DE|的最小值为 .
2
故选:B.
【题型4 向量垂直的应用】
【例4】(2023春·甘肃武威·高二统考期中)在空间,已知⃗e ,⃗e 为单位向量,且⃗e ⊥⃗e ,若⃗a=2⃗e +3⃗e ,
1 2 1 2 1 2
⃗a=k⃗e −4⃗e ,⃗a⊥⃗b,则实数k的值为( )
1 2
A.-6 B.6
C.3 D.-3
【解题思路】由⃗a和⃗b的数量积为0,解出k的值.
【解答过程】由题意可得 , , ,
⃗a⋅⃗b=0 ⃗e ⋅⃗e =0 |⃗e |=|⃗e |=1
1 2 1 2
所以(2⃗e +3⃗e )⋅(k⃗e −4⃗e )=0,即2k-12=0,得k=6.
1 2 1 2
故选:B.
【变式4-1】(2023·全国·高二专题练习)已知长方体ABCD−A B C D ,下列向量的数量积一定不为0
1 1 1 1
的是( )
A. B. C. D.
⃗AD ⋅⃗B C ⃗BD ⋅⃗AC ⃗AB⋅⃗AD ⃗BD ⋅⃗BC
1 1 1 1 1
【解题思路】当四边形ADD A 为正方形时,可证AD⊥BC可判断A;当四边形ABCD为正方形时,可证
1 1 1 1
AC⊥BD 可判断B;由长方体的性质可证AB⊥AD,分别可得数量积为0,可判断C;可推在 BCD 中,
1 1 1
∠BCD 为直角,可判BC与BD 不可能垂直,可得结论可判断D. △
1 1
【解答过程】选项A,当四边形ADD A 为正方形时,可得AD⊥AD,而AD∥BC,可得AD⊥BC,此时
1 1 1 1 1 1 1 1
有 ,故正确;
⃗AD ⋅⃗B C=0
1 1
选项B,当四边形ABCD为正方形时,可得AC⊥BD,AC⊥BB ,BD∩BB =B,
1 1
平面BBDD,可得AC⊥平面BBDD,故有AC⊥BD,此时有 ,故正确;
BD,BB ⊂ 1 1 1 1 1 ⃗BD ⋅⃗AC=0
1 1
选项C,由长方体的性质可得AB⊥平面ADD A,AD ⊂平面ADD A,可得AB⊥AD,此时必有
1 1 1 1 1 1
学科网(北京)股份有限公司0,故正确;
⃗AB⋅⃗AD =
1
选项D,由长方体的性质可得BC⊥平面CDD C ,CD ⊂平面CDD C ,可得BC⊥CD, BCD 为直角三
1 1 1 1 1 1 1
△
角形,∠BCD 为直角,故BC与BD 不可能垂直,即 ,故错误.
1 1 ⃗BD ⋅⃗BC≠0
1
故选:D.
【变式4-2】(2023春·上海杨浦·高二校考开学考试)设A、B、C、D是空间不共面的四点,且满足,
⃗AD⋅⃗AC=0,⃗AB⋅⃗AD=0,点M为BC的中点,则△AMD是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.不能确定
【解题思路】由题,可得AD⊥平面ABC,后由MA⊂平面ABC,可得答案.
【解答过程】由⃗AD⋅⃗AC=0,⃗AB⋅⃗AD=0,可知AD⊥AC,AD⊥AB.
又AC⊂平面ABC,AB⊂平面ABC,AC∩AB=A,则AD⊥平面ABC.
因M∈BC,BC⊂平面ABC,则MA⊂平面ABC.
故AD⊥MA,即△AMD是直角三角形.
故选:C.
【变式4-3】(2022秋·浙江·高二校联考期中)在如图所示的平行六面体ABCD−A′B′C′D′中,已知
1
AB=A A′=AD,∠BAD=∠BA A′=∠DA A′=60∘,⃗BM= ⃗BC,N为C′D′上一点,且⃗ D′N=λ ⃗ D′C′,
5
若DM⊥AN,则λ=( )
1 1 1 1
A. B. C. D.
2 3 4 5
【解题思路】根据空间向量基本定理,结合空间向量数量积的定义和运算性质进行求解即可.
【解答过程】设 ,
⃗AB=⃗a,⃗AD=⃗b, ⃗ A A′=⃗c
则 ,
⃗AN=⃗ A A′+⃗ A′D′+⃗ D′N=⃗ A A′+⃗AD+λ ⃗ D′C′=⃗ A A′+⃗AD+λ⃗AB=λ⃗a+⃗b+⃗c
学科网(北京)股份有限公司4 4 4
⃗DM=⃗DC+⃗CM=⃗AB+ ⃗CB=⃗AB− ⃗AD=⃗a− ⃗b,
5 5 5
⃗AN⋅⃗DM=(λ⃗a+⃗b+⃗c)⋅ ( ⃗a− 4 ⃗b ) =0,
5
4 4 4
λ⋅⃗a2− λ⋅⃗a⋅⃗b+⃗a⋅⃗b− ⋅⃗b2+⃗c⋅⃗a− ⋅⃗c⋅⃗b=0,
5 5 5
设AB=A A′=AD=m,∠BAD=∠BA A′=∠DA A′=60∘,
4 1 1 4 1 4 1
所以λ⋅m2− ⋅λm2 ⋅ +m2 ⋅ − ⋅m2+m2 ⋅ − ⋅m2 ⋅ =0,
5 2 2 5 2 5 2
1
解得λ= ,
3
故选:B.
【知识点2 向量的投影】
1.向量 的投影
(1)如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平
面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉,向量c称为向量a
在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
(2)如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为
A′,B′,得到A′B′,向量A′B′称为向量a在平面β上的投影向量.这时,向量a,A′B′的夹角就是向量a
所在直线与平面β所成的角.
【题型5 投影向量的求解】
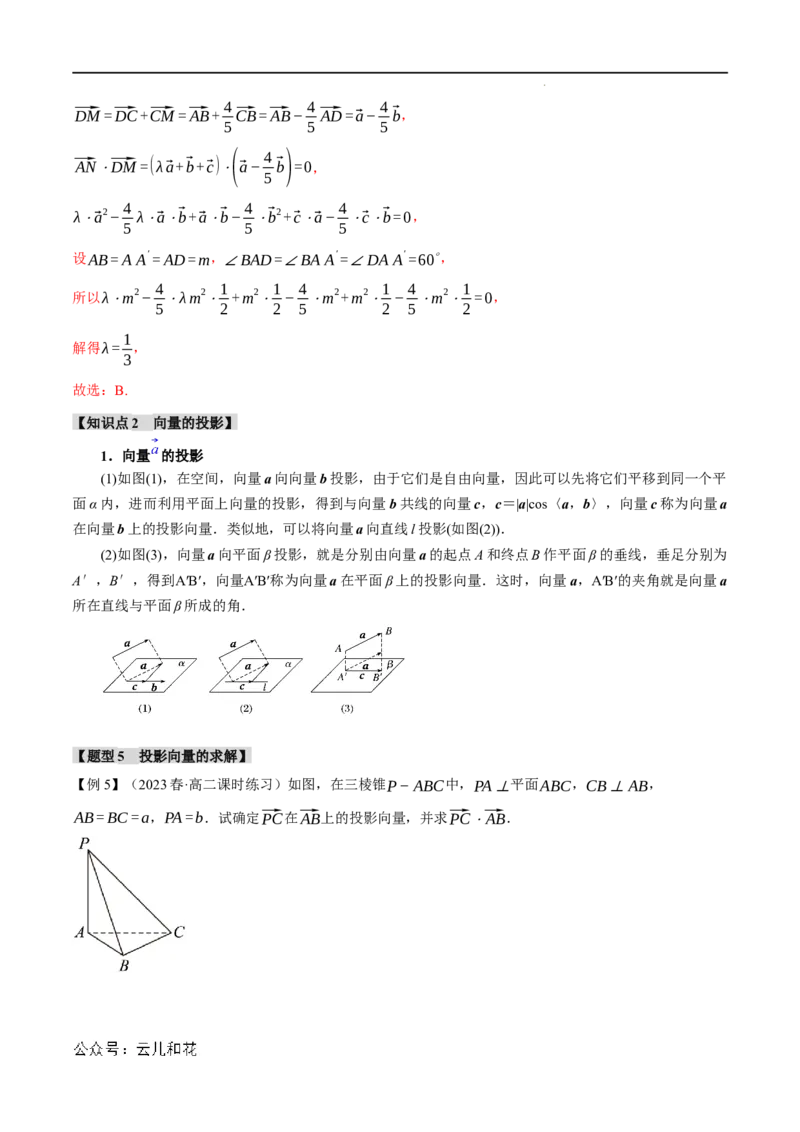
【例5】(2023春·高二课时练习)如图,在三棱锥P−ABC中,PA⊥平面ABC,CB⊥AB,
AB=BC=a,PA=b.试确定⃗PC在⃗AB上的投影向量,并求⃗PC⋅⃗AB.
学科网(北京)股份有限公司【解题思路】由题意可知 , 即可转化为 ,并化简利用数
⃗PC=⃗PA+⃗AB+⃗BC ⃗PC⋅⃗AB (⃗PA+⃗AB+⃗BC)⋅⃗AB
量积公式运算即可求得⃗PC⋅⃗AB的值;由投影向量的定义可得⃗PC在⃗AB上的投影向量为
|⃗PC|⋅cos<⃗PC,⃗AB>⋅
⃗AB
,化简运算即可等于 ⃗AB .
|⃗AB|
【解答过程】∵ PA⊥平面ABC,∴PA⊥AB,
因为 .
⃗PC⋅⃗AB=(⃗PA+⃗AB+⃗BC)⋅⃗AB=⃗PA⋅⃗AB+⃗AB⋅⃗AB+⃗BC⋅⃗AB =0+a2+0=a2
又|⃗AB|=a,
所以⃗PC在⃗AB上的投影向量为:
⃗AB ⃗PC⋅⃗AB ⃗AB ⃗PC⋅⃗AB ⃗AB a2 ⃗AB
,
|⃗PC|⋅cos<⃗PC,⃗AB>⋅ =|⃗PC|⋅ ⋅ = ⋅ = ⋅ =⃗AB
|⃗AB| |⃗PC|⋅|⃗AB| |⃗AB| |⃗AB| |⃗AB| a a
由数量积的几何意义可得: .
⃗PC⋅⃗AB=|⃗AB|⋅|⃗AB|=a2
【变式5-1】(2022·全国·高三专题练习)如图,在长方体ABCD−A′B′C′D′中,已知|AB|=1,|AD|=2,
,分别求向量 在 、 、 方向上的投影数量.
|A A′|=3 ⃑AC′ ⃑AB ⃑AD ⃑A A′
【解题思路】分析可得 ,利用投影数量公式可求得向量 在 、 、 方
⃑AC′=⃑AB+⃑AD+⃑A A′ ⃑AC′ ⃑AB ⃑AD ⃑A A′
向上的投影数量.
【解答过程】解:非零向量 在非零向量 方向上的投影数量为 ⃑a⋅⃑b ⃑a⋅⃑b,
⃑a ⃑b |⃑a|cos<⃑a,⃑b>=|⃑a|⋅ =
|⃑a|⋅|⃑b| |⃑b|
由空间向量的平行六面体法则可得 ,
⃑AC′=⃑AB+⃑AD+⃑A A′
学科网(北京)股份有限公司在长方体 中, ,
ABCD−A′B′C′D′ ⃑AB⋅⃑AD=⃑AB⋅ ⃑A A′=⃑AD⋅ ⃑A A′=0
因此,向量 在 方向上的投影数量为 ⃑AC′ ⋅⃑AB (⃑AB+⃑AD+⃑A A′) ⋅⃑AB ,
⃑AC′ ⃑AB = =|⃑AB|=1
|⃑AB| |⃑AB|
向量 在 方向上的投影数量为 ⃑AC′ ⋅⃑AD (⃑AB+⃑AD+⃑A A′) ⋅⃑AD ,
⃑AC′ ⃑AD = =|⃑AD|=2
|⃑AD| |⃑AD|
向量⃑AC′ 在⃑A A′ 方向上的投影数量为 ⃑AC′ ⋅ ⃑A A′ = (⃑AB+⃑AD+⃑A A′) ⋅ ⃑A A′ =|⃑A A′|=3.
|⃑A A′| |⃑A A′|
【变式5-2】(2023春·高二课时练习)如图,在三棱锥PABC中,PA⊥平面ABC,CB⊥AB, AB=BC=
a, PA=b.试确定⃗PC在直线AB上的投影向量,并求⃗PC⋅⃗AB.
【解题思路】由图形特征,用⃗PA,⃗AB,⃗BC为基底表示⃗PC,计算数量积和投影向量.
【解答过程】因为 .
⃗PC⋅⃗AB=(⃗PA+⃗AB+⃗BC)⋅⃗AB=⃗PA⋅⃗AB+⃗AB⋅⃗AB+⃗BC⋅⃗AB =0+a2+0=a2
又|⃗AB|=a,
所以⃗PC在⃗AB上的投影向量为:
|⃗PC|⋅cos⟨⃗PC,⃗AB⟩⋅
⃗AB
=|⃗PC|⋅
⃗PC⋅⃗AB
⋅
⃗AB
=
⃗PC⋅⃗AB
⋅
⃗AB
=
a2
⋅
⃗AB
=⃗AB .
|⃗AB| |⃗PC|⋅|⃗AB| |⃗AB| |⃗AB| |⃗AB| a a
【变式5-3】(2023春·高二课时练习)如图,在三棱锥P−ABC中,PA⊥平面ABC,CB⊥AB,
AB=BC=a,PA=b.
学科网(北京)股份有限公司(1)确定⃑PC在平面ABC上的投影向量,并求⃑PC⋅⃑AB;
(2)确定⃑PC在⃑AB上的投影向量,并求⃑PC⋅⃑AB.
【解题思路】(1)根据PA⊥平面ABC可得⃑PC在平面ABC上的投影向量,由空间向量的线性运算以及
数量积的定义计算⃑PC⋅⃑AB=(⃑PA+⃑AB+⃑BC)⋅⃑AB的值即可求解;
(2)由投影向量的定义可得⃑PC在⃑AB上的投影向量,由数量积的几何意义可得⃑PC⋅⃑AB的值.
【解答过程】(1)因为PA⊥平面ABC,所以⃑PC在平面ABC上的投影向量为⃑AC,
因为PA⊥平面ABC,AB⊂面ABC,可得PA⊥AB,所以⃑PA⋅⃑AB=0,
因为CB⊥AB,所以⃑BC⋅⃑AB=0,
所以⃑PC⋅⃑AB=(⃑PA+⃑AB+⃑BC)⋅⃑AB=⃑PA⋅⃑AB+⃑AB⋅⃑AB+⃑BC⋅⃑AB
=0+a2+0=a2.
(2)由(1)知:⃑PC⋅⃑AB=a2,|⃑AB|=a,
所以⃑PC在⃑AB上的投影向量为:
⃑AB ⃑PC⋅⃑AB ⃑AB ⃑PC⋅⃑AB ⃑AB a2 ⃑AB ,
|⃑PC|⋅cos⟨⃑PC,⃑AB⟩⋅ =|⃑PC|⋅ ⋅ = ⋅ = ⋅ =⃑AB
|⃑AB| |⃑PC|⋅|⃑AB| |⃑AB| |⃑AB| |⃑AB| a a
由数量积的几何意义可得:⃑PC⋅⃑AB=|⃑AB|⋅|⃑AB|=a2
.
学科网(北京)股份有限公司