文档内容
专题 1.7 空间向量与立体几何全章八类必考压轴题
【人教A版(2019)】
【考点1 空间向量的线性运算】
1
1.(2023·全国·高三对口高考) (⃗a+2⃗b−3⃗c)−3(⃗a−2⃗b−⃗c)=( )
2
5 5 5 3 5 9
A.− ⃗a−4⃗c B.− ⃗a+4⃗b−2⃗c C.− ⃗a+7⃗b+ ⃗c D.− ⃗a−5⃗b− ⃗c
2 2 2 2 2 2
【解题思路】根据向量的线性运算求解即可.
1 5 3
【解答过程】 (⃗a+2⃗b−3⃗c)−3(⃗a−2⃗b−⃗c)=− ⃗a+7⃗b+ ⃗c.
2 2 2
故选:C.
2.(2023春·安徽合肥·高二校考期末)已知⃗a=(1,2,1),⃗b=(2,−4,1),则2⃗a+⃗b等于( )
A.(4,−2,0) B.(4,0,3)
C.(−4,0,3) D.(4,0,−3)
【解题思路】根据向量坐标运算即可.
【解答过程】2⃗a+⃗b=2(1,2,1)+(2,−4,1)=(4,0,3).
故选:B.
3.(2023春·高二课时练习)已知向量⃗a=(−2,−3,1),⃗b=(2,0,3),⃗c=(0,0,2),则⃗a+6⃗b−⃗c的坐标为
(10,−3,17) .
【解题思路】直接利用向量的运算法则计算即可.
【解答过程】向量⃗a=(−2,−3,1),⃗b=(2,0,3),⃗c=(0,0,2),则
⃗a+6⃗b−⃗c=(−2,−3,1)+6(2,0,3)−(0,0,2)=(10,−3,17).
故答案为:(10,−3,17).
4.(2023春·高二课时练习)已知⃗a=(1,−3,8),⃗b=(3,10,−4),求⃗a+⃗b,⃗a−⃗b,3⃗a.
【解题思路】直接根据向量的加减数乘的坐标运算即可得解.
学科网(北京)股份有限公司【解答过程】⃑a+⃑b=(1,−3,8)+(3,10,−4)=(1+3,−3+10,8−4)=(4,7,4),
⃑a−⃑b=(1,−3,8)−(3,10,−4)=(1−3,−3−10,8+4)=(−2,−13,12),
3⃑a=3(1,−3,8)=(3×1,3×(−3),3×8)=(3,−9,24).
5.(2023春·高二课时练习)如图所示,在三棱柱ABC−A B C 中,M是BB 的中点,化简下列各式,
1 1 1 1
并在图中标出化简得到的向量.
(1)⃑CB+⃑BA ;
1
1
(2)⃑AC+⃑CB+ ⃑A A ;
2 1
1 1
(3) ⃑A A − ⃑B B−⃑AC−⃑CB.
2 1 2 1
【解题思路】(1)(2)(3)利用空间向量的加减法的运算法则和几何意义化简.
【解答过程】(1)解:⃑CB+⃑BA =⃑C A .
1 1
1
(2)解:因为M是BB 的中点,所以⃑BM= ⃑BB ,又⃑A A =⃑BB ,
1 2 1 1 1
1
所以⃑AC+⃑CB+ ⃑A A =⃑AB+⃑BM=⃑AM.
2 1
学科网(北京)股份有限公司1 1
(3)解: ⃑A A − ⃑B B−⃑AC−⃑CB
2 1 2 1
1
= (⃑A A +⃑BB )−(⃑AC+⃑CB)=⃑A A −⃑AB=⃑BA
2 1 1 1 1
【考点2 空间向量数量积的应用】
1.(2023春·福建泉州·高二校联考期末)平行六面体ABCD−A B C D 的所有棱长均为1,
1 1 1 1
∠BAD=∠BA A =∠DA A =60°,则AC 的长度为( )
1 1 1
3√2
A. B.√6 C.3 D.6
2
【解题思路】由ABCD−A B C D 为平行六面体,可知AC 为体对角线,由向量的模长公式即可求得
1 1 1 1 1
AC .
1
【解答过程】|⃗AC |=|⃗AB+⃗AD+⃗A A |=√(⃗AB+⃗AD+⃗A A ) 2
1 1 1
= √|⃗AB| 2 +|⃗AD| 2 +|⃗A A | 2 +2|⃗AB||⃗AD|⋅cos60°+2|⃗AB||⃗A A |⋅cos60°+2|⃗A A ||⃗AD|⋅cos60°
1 1 1
学科网(北京)股份有限公司√ 1 1 1
= 1+1+1+2×1×1× +2×1×1× +2×1×1×
2 2 2
=√6,
故选:B.
2.(2023春·甘肃金昌·高二校考期中)如图,在平行六面体ABCD−A B C D 中,AB=2,AD=2,
1 1 1 1
A A =2,∠BA A =∠DA A =60°,∠BAD=90°,则BC 与C A 所成角的余弦值为( )
1 1 1 1 1
√3 √3 √2 √2
A.− B. C.− D.
6 6 4 4
【解题思路】根据空间向量的基本定理和向量的数量积的定义即可求解.
【解答过程】设⃗AB=⃗a,⃗AD=⃗b,⃗A A =⃗c,
1
因为⃗a,⃗b,⃗c向量不共面,故{⃗a,⃗b,⃗c}可构成空间的一组基底,
结合|⃗a|=2,|⃗b|=2,|⃗c|=2,∠BA A =∠DA A =60°,∠BAD=90°,
1 1
1 1
所以⃗a⋅⃗b=0,⃗a⋅⃗c= 2×2× =2,⃗b⋅⃗c=2×2× =2,
2 2
则⃗BC =⃗b+⃗c,⃗C A =−⃗a−⃗b+⃗c,
1 1
可得⃗BC ⋅⃗C A =(⃗b+⃗c)⋅(−⃗a−⃗b+⃗c) =−⃗a⋅⃗b−⃗a⋅⃗c−⃗b2−⃗b⋅⃗c+⃗c⋅⃗b+⃗c2
1 1
=0−2−4+4 =−2,
|⃗BC | =√(⃗b+⃗c) 2 =√⃗b2+2⃗b⋅⃗c+⃗c2 =√4+2×2+4 =2√3,
1
|⃗C A |=√(−⃗a−⃗b+⃗c) 2 =√⃗a2+⃗b2+⃗c2+2⃗a⋅⃗b−2⃗a⋅⃗c−2⃗b⋅⃗c
1
=√4+4+4+0−4−4 =2,
⃗BC ⋅⃗C A −2 √3
所以cos⟨⃗BC ,⃗C A ⟩= 1 1 = =− ,
1 1 |⃗BC ||⃗C A | 2√3×2 6
1 1
学科网(北京)股份有限公司( π]
又因为异面直线所成角的范围是 0, ,
2
√3
所以BC 与C A 所成角的余弦值为 .
1 1 6
故选:B.
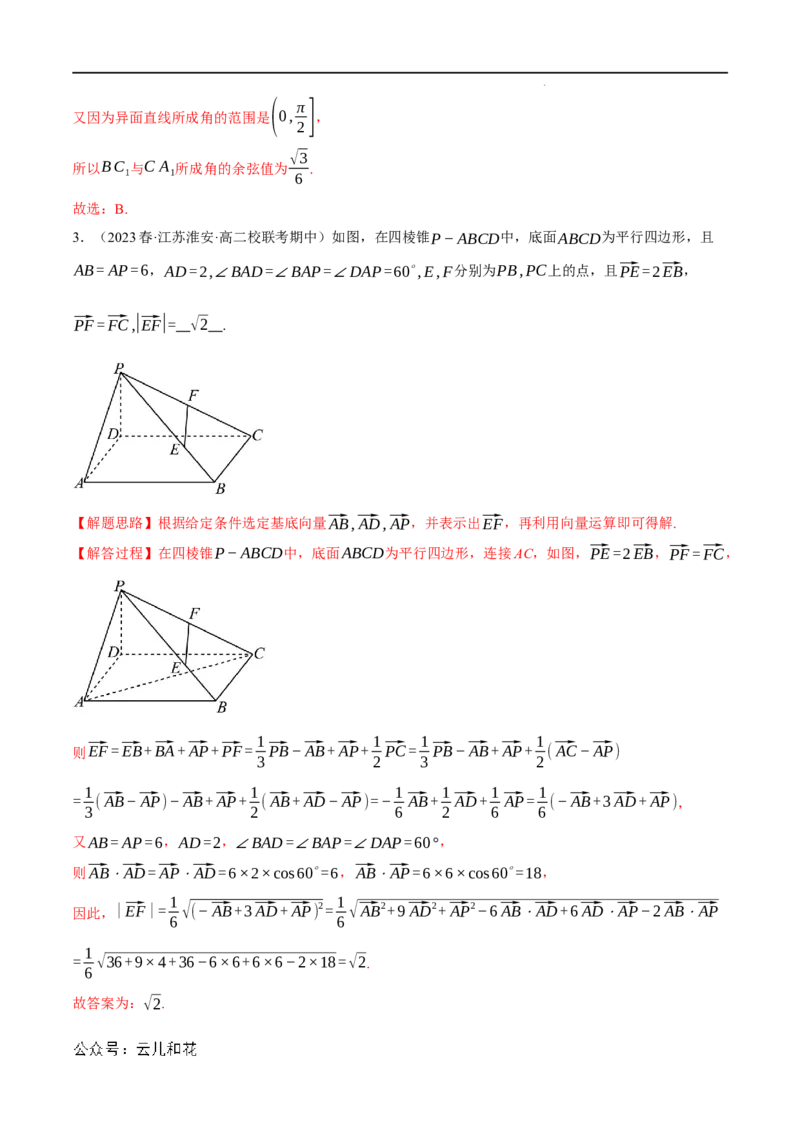
3.(2023春·江苏淮安·高二校联考期中)如图,在四棱锥P−ABCD中,底面ABCD为平行四边形,且
AB=AP=6,AD=2,∠BAD=∠BAP=∠DAP=60∘,E,F分别为PB,PC上的点,且⃗PE=2⃗EB,
⃗PF=⃗FC,|⃗EF|= √2 .
【解题思路】根据给定条件选定基底向量⃗AB,⃗AD,⃗AP,并表示出⃗EF,再利用向量运算即可得解.
【解答过程】在四棱锥P−ABCD中,底面ABCD为平行四边形,连接AC,如图,⃗PE=2⃗EB,⃗PF=⃗FC,
1 1 1 1
则⃗EF=⃗EB+⃗BA+⃗AP+⃗PF= ⃗PB−⃗AB+⃗AP+ ⃗PC= ⃗PB−⃗AB+⃗AP+ (⃗AC−⃗AP)
3 2 3 2
1 1 1 1 1 1
= (⃗AB−⃗AP)−⃗AB+⃗AP+ (⃗AB+⃗AD−⃗AP)=− ⃗AB+ ⃗AD+ ⃗AP= (−⃗AB+3⃗AD+⃗AP),
3 2 6 2 6 6
又AB=AP=6,AD=2,∠BAD=∠BAP=∠DAP=60°,
则⃗AB⋅⃗AD=⃗AP⋅⃗AD=6×2×cos60∘=6,⃗AB⋅⃗AP=6×6×cos60∘=18,
1 1
因此,|⃗EF|= √(−⃗AB+3⃗AD+⃗AP) 2= √⃗AB2+9⃗AD2+⃗AP2−6⃗AB⋅⃗AD+6⃗AD⋅⃗AP−2⃗AB⋅⃗AP
6 6
1
= √36+9×4+36−6×6+6×6−2×18=√2.
6
故答案为:√2.
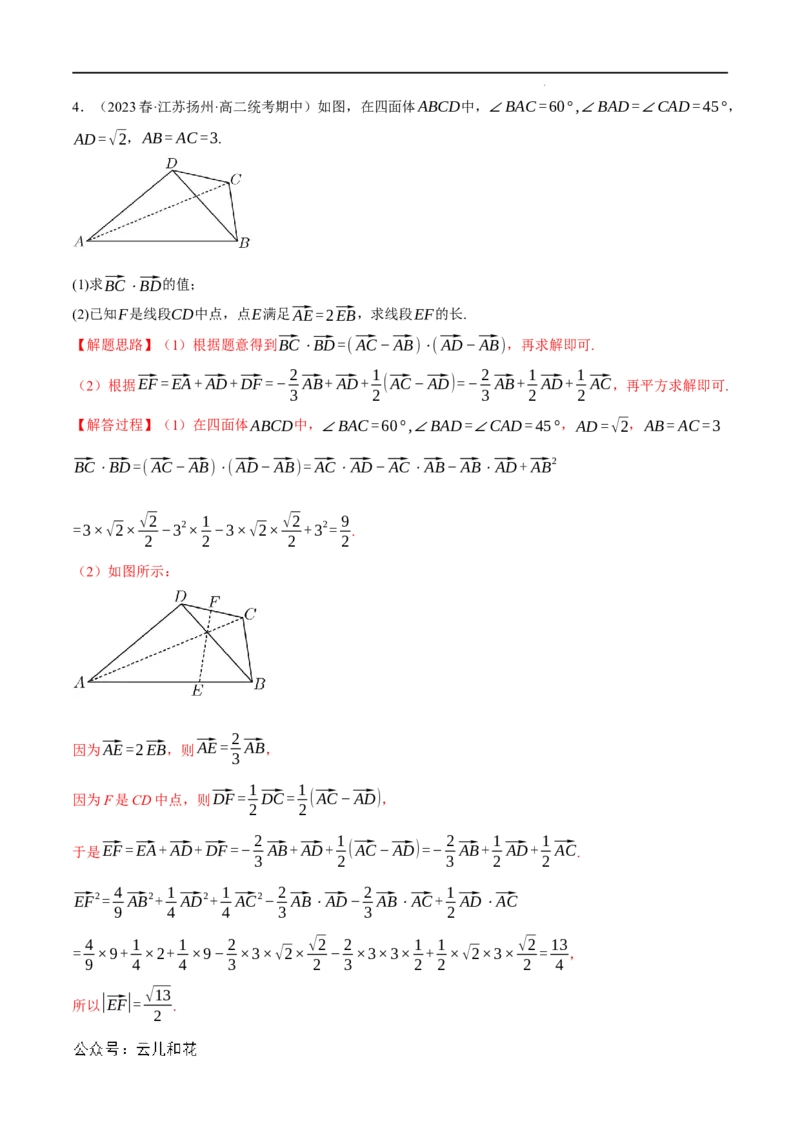
学科网(北京)股份有限公司4.(2023春·江苏扬州·高二统考期中)如图,在四面体ABCD中,∠BAC=60°,∠BAD=∠CAD=45°,
AD=√2,AB=AC=3.
(1)求⃗BC⋅⃗BD的值;
(2)已知F是线段CD中点,点E满足⃗AE=2⃗EB,求线段EF的长.
【解题思路】(1)根据题意得到⃗BC⋅⃗BD=(⃗AC−⃗AB)⋅(⃗AD−⃗AB),再求解即可.
2 1 2 1 1
(2)根据⃗EF=⃗EA+⃗AD+⃗DF=− ⃗AB+⃗AD+ (⃗AC−⃗AD)=− ⃗AB+ ⃗AD+ ⃗AC,再平方求解即可.
3 2 3 2 2
【解答过程】(1)在四面体ABCD中,∠BAC=60°,∠BAD=∠CAD=45°,AD=√2,AB=AC=3
⃗BC⋅⃗BD=(⃗AC−⃗AB)⋅(⃗AD−⃗AB)=⃗AC⋅⃗AD−⃗AC⋅⃗AB−⃗AB⋅⃗AD+⃗AB2
√2 1 √2 9
=3×√2× −32× −3×√2× +32= .
2 2 2 2
(2)如图所示:
2
因为⃗AE=2⃗EB,则⃗AE= ⃗AB,
3
1 1
因为F是CD中点,则⃗DF= ⃗DC= (⃗AC−⃗AD),
2 2
2 1 2 1 1
于是⃗EF=⃗EA+⃗AD+⃗DF=− ⃗AB+⃗AD+ (⃗AC−⃗AD)=− ⃗AB+ ⃗AD+ ⃗AC.
3 2 3 2 2
4 1 1 2 2 1
⃗EF2= ⃗AB2+ ⃗AD2+ ⃗AC2− ⃗AB⋅⃗AD− ⃗AB⋅⃗AC+ ⃗AD⋅⃗AC
9 4 4 3 3 2
4 1 1 2 √2 2 1 1 √2 13
= ×9+ ×2+ ×9− ×3×√2× − ×3×3× + ×√2×3× = ,
9 4 4 3 2 3 2 2 2 4
√13
所以|⃗EF|=
.
2
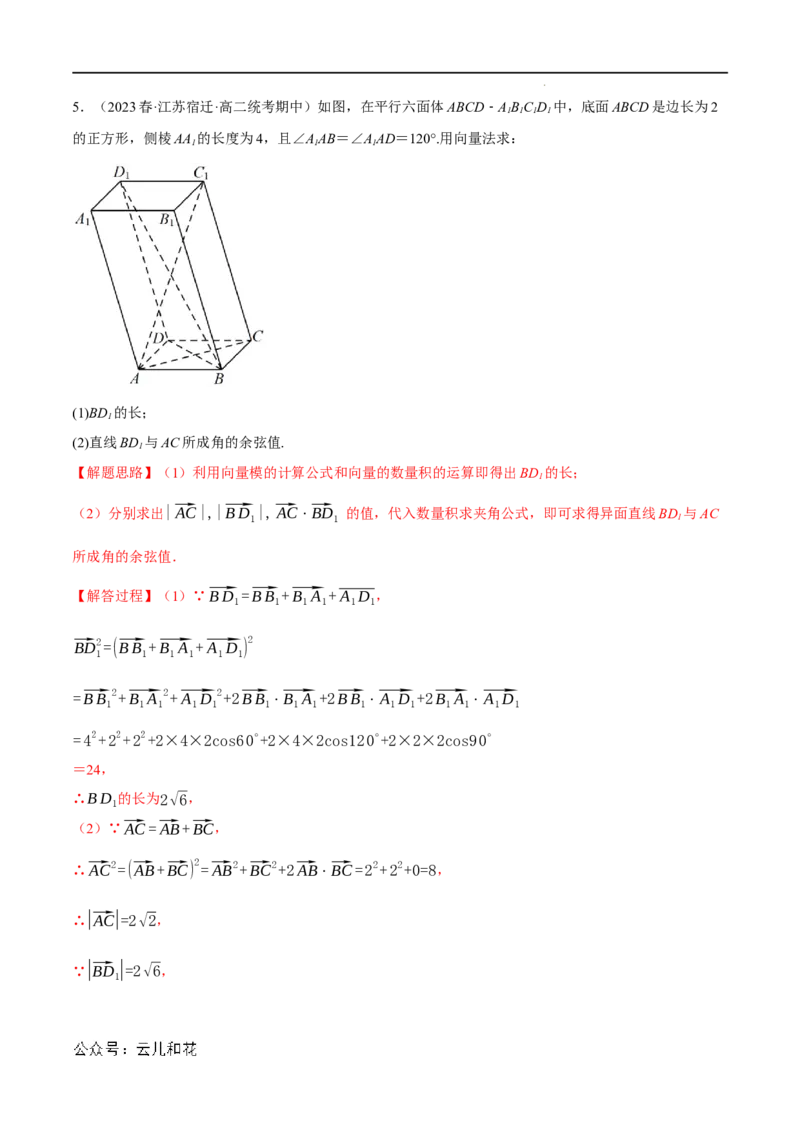
学科网(北京)股份有限公司5.(2023春·江苏宿迁·高二统考期中)如图,在平行六面体ABCD﹣ABC D 中,底面ABCD是边长为2
1 1 1 1
的正方形,侧棱AA 的长度为4,且∠AAB=∠AAD=120°.用向量法求:
1 1 1
(1)BD 的长;
1
(2)直线BD 与AC所成角的余弦值.
1
【解题思路】(1)利用向量模的计算公式和向量的数量积的运算即得出BD 的长;
1
(2)分别求出|⃗AC|,|⃗BD |,⃗AC⋅⃗BD 的值,代入数量积求夹角公式,即可求得异面直线BD 与AC
1 1 1
所成角的余弦值.
【解答过程】(1)∵⃗BD =⃗BB +⃗B A +A D ,
1 1 1 1 1 1
⃗BD2=(⃗BB +⃗B A +⃗A D ) 2
1 1 1 1 1 1
=⃗BB 2+⃗B A 2+⃗A D 2+2⃗BB ⋅⃗B A +2⃗BB ⋅⃗A D +2⃗B A ⋅⃗A D
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
=42+22+22+2×4×2cos60∘+2×4×2cos120∘+2×2×2cos90∘
=24,
∴BD 的长为2√6,
1
(2)∵⃗AC=⃗AB+⃗BC,
∴⃗AC2=(⃗AB+⃗BC) 2 =⃗AB2+⃗BC2+2⃗AB⋅⃗BC=22+22+0=8,
∴|⃗AC|=2√2,
∵|⃗BD |=2√6,
1
学科网(北京)股份有限公司⃗AC⋅⃗BD =(⃗AB+⃗BC)⋅(⃗BB +⃗B A +⃗A D )
1 1 1 1 1 1
=⃗AB⋅⃗BB +⃗AB⋅⃗B A +⃗AB⋅⃗A D +⃗BC⋅⃗BB +⃗BC⋅⃗B A +⃗BC⋅⃗A D
1 1 1 1 1 1 1 1 1 1 ,
=2×4cos120∘+2×2cos180∘+2×2cos90∘+2×4cos120∘+2×2cos90∘+2×2cos0∘
=−8
∴
|cos⟨⃗AC,⃗BD ⟩|=
| ⃗AC⋅⃗BD
1
|
=
| −8 |
=
√12
=
√3
,
1 |⃗AC|⋅|⃗BD | 2√2×2√6 12 3
1
√3
所以直线BD 与AC所成角的余弦值为 .
1 3
【考点3 空间向量基本定理及其应用】
1.(2023春·安徽池州·高二联考阶段练习)已知{⃗a,⃗b,⃗c}是空间的一组基底,其中⃗AB=2⃗a−3⃗b,
⃗AC=⃗a−⃗c,⃗AD=2⃗b+λ⃗c.若A,B,C,D四点共面,则λ=( )
3 3 4 4
A.− B. C. D.−
4 4 3 3
【解题思路】根据题意,设存在唯一的实数对(x,y),使得⃗AB=x⃗AC+ y⃗AD,结合向量的数乘运算和相
等向量的概念计算,即可求解.
【解答过程】由题意,设存在唯一的实数对(x,y),使得⃗AB=x⃗AC+ y⃗AD,
即2⃗a−3⃗b=x(⃗a−⃗c)+ y(2⃗b+λ⃗c),
则2⃗a−3⃗b=x⃗a+2y⃗b+(λy−x)⃗c,
3 4
则x=2,y=− ,λy−x=0,解得λ=− .
2 3
故选:D.
2.(2023春·江苏泰州·高二统考期末)已知三棱柱ABC−A B C 的侧棱长为2,底面ABC是边长为2
1 1 1
的正三角形,∠A AB=∠A AC=60°,若B C和BC 相交于点M.则|⃗AM|=( )
1 1 1 1
A.√3 B.2 C.√5 D.√6
【解题思路】以{⃗AB,⃗AC,⃗A A }为基底表示⃗AM,利用平方的方法求得|⃗AM|.
1
【解答过程】依题意可知M是BC 的中点,
1
1 1 1
所以⃗AM= (⃗AC +⃗AB)= ⃗AC + ⃗AB
2 1 2 1 2
学科网(北京)股份有限公司1 1 1 1 1
= (⃗AC+⃗A A )+ ⃗AB= ⃗AC+ ⃗A A + ⃗AB,
2 1 2 2 2 1 2
所以|⃗AM|=√(⃗AM) 2 = √1 (⃗AC+⃗A A +⃗AB) 2
4 1
1
= √⃗AC2+⃗A A 2+⃗AB2+2(⃗AC⋅⃗A A +⃗AC⋅⃗AB+⃗A A ⋅⃗AB)
2 1 1 1
1
= √4+4+4+2(2⋅2⋅cos60°×3)=√6.
2
故选:D.
3.(2022·湖北十堰·高三校考阶段练习)如图,已知空间四边形OABC,其对角线为OB,AC,M,N
分别为OA,BC的中点,点G在线段MN上,且⃑MG=2⃑GN,若⃑OG=x⃑OA+ y⃑OB+z⃑OC,则x+ y+z=
5
.
6
【解题思路】以⃑OA,⃑OB,⃑OC为一组基向量,首先⃑OG=⃑OM+⃑MG,再将⃑OM,⃑MG逐步地用基向量表示,
最后合并整理得出结果.
【解答过程】由M,N分别为OA,BC的中点,点G在线段MN上,
且⃑MG=2⃑GN,
1 2
所以⃑OG=⃑OM+⃑MG= ⃑OA+ ⃑MN
2 3
1 2
= ⃑OA+ (⃑ON−⃑OM)
2 3
学科网(北京)股份有限公司1 2[1 1 ]
= ⃑OA+ (⃑OB+⃑OC)− ⃑OA
2 3 2 2
1 1 1
= ⃑OA+ ⃑OB+ ⃑OC,
6 3 3
5
则x+ y+z= ,
6
5
故答案为: .
6
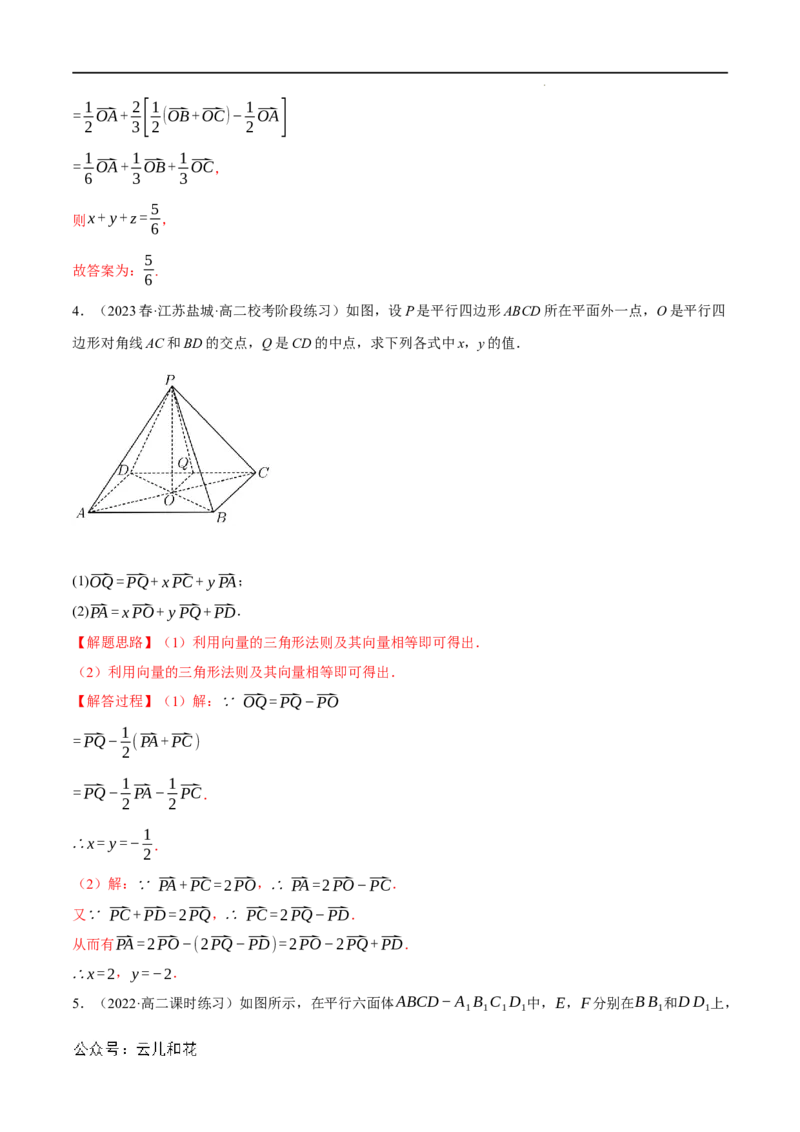
4.(2023春·江苏盐城·高二校考阶段练习)如图,设P是平行四边形ABCD所在平面外一点,O是平行四
边形对角线AC和BD的交点,Q是CD的中点,求下列各式中x,y的值.
(1)⃑OQ=⃑PQ+x⃑PC+ y⃑PA;
(2)⃑PA=x⃑PO+ y⃑PQ+⃑PD.
【解题思路】(1)利用向量的三角形法则及其向量相等即可得出.
(2)利用向量的三角形法则及其向量相等即可得出.
【解答过程】(1)解:∵ ⃑OQ=⃑PQ−⃑PO
1
=⃑PQ− (⃑PA+⃑PC)
2
1 1
=⃑PQ− ⃑PA− ⃑PC.
2 2
1
∴x= y=− .
2
(2)解:∵ ⃑PA+⃑PC=2⃑PO,∴ ⃑PA=2⃑PO−⃑PC.
又∵ ⃑PC+⃑PD=2⃑PQ,∴ ⃑PC=2⃑PQ−⃑PD.
从而有⃑PA=2⃑PO−(2⃑PQ−⃑PD)=2⃑PO−2⃑PQ+⃑PD.
∴x=2,y=−2.
5.(2022·高二课时练习)如图所示,在平行六面体ABCD−A B C D 中,E,F分别在BB 和DD 上,
1 1 1 1 1 1
学科网(北京)股份有限公司1 2
且BE= BB ,DF= DD .
3 1 3 1
(1)证明:A、E、C 、F四点共面.
1
(2)若⃑EF=x⃑AB+ y⃑AD+z⃑A A ,求x+ y+z.
1
1
【解题思路】(1)在CC 上取一点G,使得CG= CC ,连接EG、DG,根据平行六面体的性质
1 3 1
DG//FC 、AE//DG,即可得到AE//FC ,即可得证;
1 1
(2)结合图形,根据空间向量线性运算法则计算可得.
1
【解答过程】(1)证明:在CC 上取一点G,使得CG= CC ,连接EG、DG,
1 3 1
1 2 1
在平行六面体ABCD−A B C D 中,BE= BB ,DF= DD ,CG= CC ,
1 1 1 1 3 1 3 1 3 1
∴DF//C G且DF=C G,BE//CG且BE=CG,
1 1
所以四边形DFC G为平行四边形,四边形BEGC为平行四边形,
1
所以DG//FC ,EG//BC且EG=BC,
1
又AD//BC且AD=BC,
所以EG//AD且EG=AD,
所以四边形AEGD为平行四边形,
所以AE//DG,
所以AE//FC ,
1
∴A、E、C 、F四点共面.
1
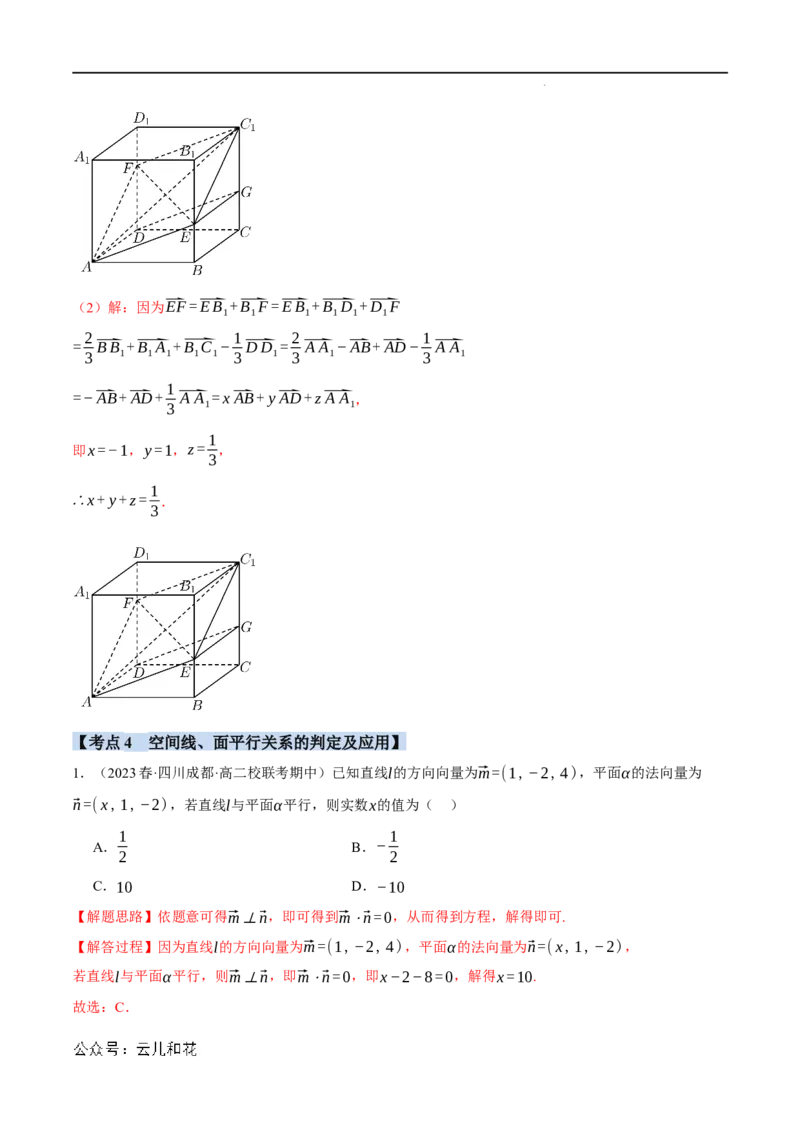
学科网(北京)股份有限公司(2)解:因为⃑EF=⃑EB +⃑B F=⃑EB +⃑B D +⃑D F
1 1 1 1 1 1
2 1 2 1
= ⃑BB +⃑B A +⃑B C − ⃑DD = ⃑A A −⃑AB+⃑AD− ⃑A A
3 1 1 1 1 1 3 1 3 1 3 1
1
=−⃑AB+⃑AD+ ⃑A A =x⃑AB+ y⃑AD+z⃑A A ,
3 1 1
1
即x=−1,y=1,z= ,
3
1
∴x+ y+z= .
3
【考点4 空间线、面平行关系的判定及应用】
1.(2023春·四川成都·高二校联考期中)已知直线l的方向向量为⃗m=(1,−2,4),平面α的法向量为
⃗n=(x,1,−2),若直线l与平面α平行,则实数x的值为( )
1 1
A. B.−
2 2
C.10 D.−10
【解题思路】依题意可得⃗m⊥⃗n,即可得到⃗m⋅⃗n=0,从而得到方程,解得即可.
【解答过程】因为直线l的方向向量为⃗m=(1,−2,4),平面α的法向量为⃗n=(x,1,−2),
若直线l与平面α平行,则⃗m⊥⃗n,即⃗m⋅⃗n=0,即x−2−8=0,解得x=10.
故选:C.
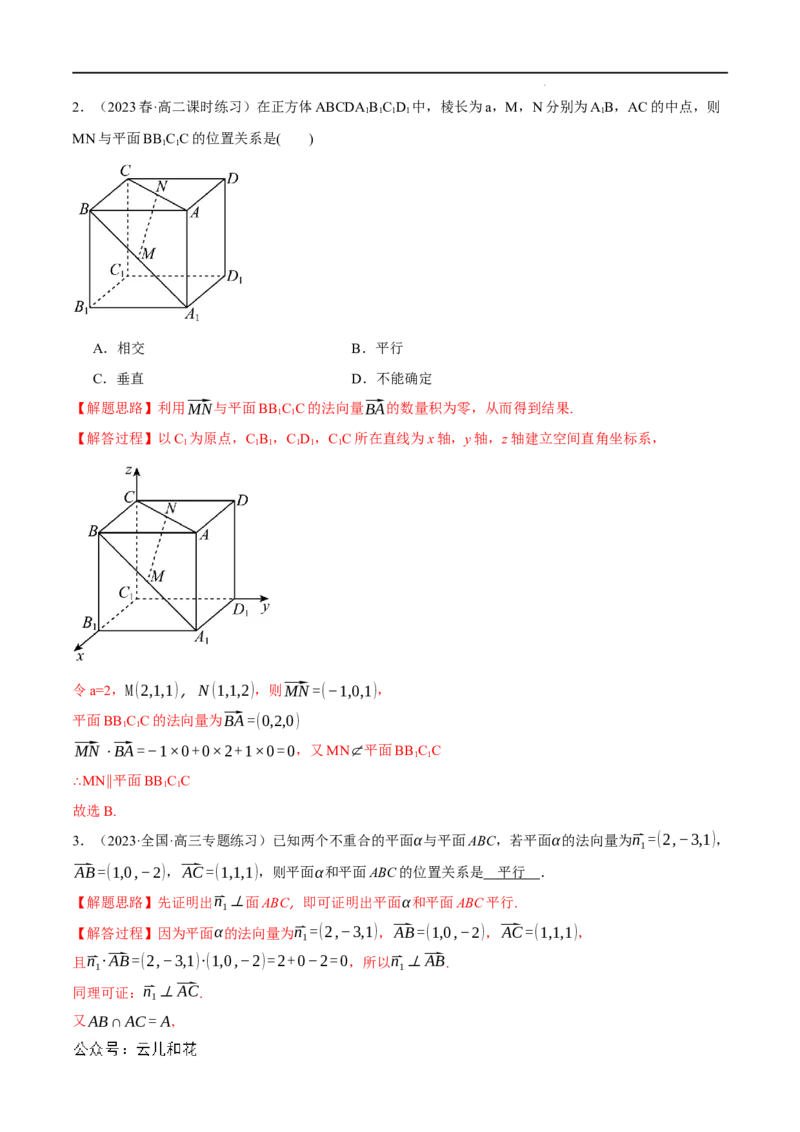
学科网(北京)股份有限公司2.(2023春·高二课时练习)在正方体ABCDAB C D 中,棱长为a,M,N分别为AB,AC的中点,则
1 1 1 1 1
MN与平面BB C C的位置关系是( )
1 1
A.相交 B.平行
C.垂直 D.不能确定
【解题思路】利用⃗MN与平面BB C C的法向量⃗BA的数量积为零,从而得到结果.
1 1
【解答过程】以C 为原点,C B ,C D,C C所在直线为x轴,y轴,z轴建立空间直角坐标系,
1 1 1 1 1 1
令a=2,M(2,1,1),N(1,1,2),则⃗MN=(−1,0,1),
平面BB C C的法向量为⃗BA=(0,2,0)
1 1
⃗MN⋅⃗BA=−1×0+0×2+1×0=0,又MN⊄平面BB C C
1 1
∴MN∥平面BB C C
1 1
故选B.
3.(2023·全国·高三专题练习)已知两个不重合的平面α与平面ABC,若平面α的法向量为⃑n =(2,−3,1),
1
⃑AB=(1,0,−2),⃑AC=(1,1,1),则平面α和平面ABC的位置关系是 平行 .
【解题思路】先证明出⃑n ⊥面ABC,即可证明出平面α和平面ABC平行.
1
【解答过程】因为平面α的法向量为⃑n =(2,−3,1),⃑AB=(1,0,−2),⃑AC=(1,1,1),
1
且⃑n ·⃑AB=(2,−3,1)·(1,0,−2)=2+0−2=0,所以⃑n ⊥⃑AB.
1 1
同理可证:⃑n ⊥⃑AC.
1
又AB∩AC=A,
学科网(北京)股份有限公司所以⃑n ⊥面ABC.
1
又⃑n 为面α的法向量,
1
所以面α//面ABC.
故答案为:平行.
4.(2023·江苏·高二专题练习)在正方体ABCD-ABC D 中,点P在线段AD上,点Q在线段AC上,线
1 1 1 1 1
段PQ与直线AD和AC都垂直,求证:PQ∥BD.
1 1
→
【解题思路】建立空间直角坐标系,利用向量垂直的坐标运算求出
PQ
,再根据共线向量证明即可.
【解答过程】证明:以点D为坐标原点,建立如图所示的空间直角坐标系,设正方体的棱长为1,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),A(1,0,1),D(0,0,1),
1 1
→ → →
∴D A =(1,0,1), AC =(-1,1,0),设 PQ =(a,b,c),
1
→
则¿即¿取 PQ=(1,1,-1).
→
易知BD =(−1,−1,1) ,
1
→ →
∴ PQ= −BD ,
1
学科网(北京)股份有限公司→ →
∴PQ//BD ,
1
即PQ∥BD.
1
5.(2023·全国·高二专题练习)在正方体ABCD−A B C D 中,点E,F分别是正方形A B C D 和正
1 1 1 1 1 1 1 1
方形B C CB的中心.求证:
1 1
(1)AC ⊥平面A BD;
1 1
(2)EF//平面A BD;
1
(3)平面B EF∥平面A BD.
1 1
【解题思路】(1)建立空间直角坐标系,利用向量法证得AC ⊥平面A BD;
1 1
(2)利用向量法证得EF//平面A BD;
1
(3)利用向量法证得平面B EF∥平面A BD.
1 1
【解答过程】(1)设正方体的边长为2,建立如图所示空间直角坐标系,
C (2,2,2),A (0,0,2),B(2,0,0),D(0,2,0),
1 1
⃑A B=(2,0,−2),⃑A D=(0,2,−2),
1 1
⃑AC ⋅⃑A B=0,⃑AC ⋅⃑A D=0,
1 1 1 1
所以AC ⊥A B,AC ⊥A D,
1 1 1 1
由于A B∩A D=A ,所以AC ⊥平面A BD.
1 1 1 1 1
(2)设平面A BD的法向量为⃑n =(x ,y ,z ),
1 1 1 1 1
则¿,故可设⃑n =(1,1,1).
1
E(1,1,2),F(2,1,1),⃑EF=(1,0,−1),
⃑n ⋅⃑EF=0,E,F∉平面A BD,
1 1
所以EF//平面A BD.
1
(3)B (2,0,2),⃑B F=(0,1,−1),
1 1
设平面B EF的法向量为⃑n =(x ,y ,z ),
1 2 2 2 2
则¿,故可设⃑n =(1,1,1).
2
⃑n =⃑n ,
1 2
显然,平面B EF与平面A BD不重合,所以平面B EF∥平面A BD.
1 1 1 1
学科网(北京)股份有限公司【考点5 空间线、面垂直关系的判定及应用】
1.(2022秋·四川达州·高二统考期末)长方体ABCD−A B C D 中,
1 1 1 1
AB=3,BC=4,A A =5,AC∩BD=O,M为CC 中点,则下列选项中与OM垂直的是( )
1 1
A.OA B.BC C.OB D.A C
1 1 1
【解题思路】建立空间直角坐标系,然后利用空间向量逐个分析判断即可.
【解答过程】如图,以D为原点,以DA,DC,DD 所在的直线分别为x,y,z轴建立空间直角坐标系,
1
则D(0,0,0),A(4,0,0),B(4,3,0),C(0,3,0),A (4,0,5),B (4,3,5),C (0,3,5),
1 1 1
因为AC∩BD=O,M为CC 中点,
1
3 5
所以O(2, ,0),M(0,3, ),
2 2
3 5
所以⃗OM=(−2, , ),
2 2
3 9 25 25
对于A,⃗OA =(2,− ,5),则⃗OA ⋅⃗OM=−4− + = ≠0,所以OM与OA 不垂直,所以A错
1 2 1 4 2 4 1
误,
对于B,⃗BC=(−4,0,0),则⃗BC⋅⃗OM=8≠0,所以OM与BC不垂直,所以B错误,
3 9 25
对于C,⃗OB =(2, ,5),则⃗OB ⋅⃗OM=−4+ + ≠0,所以OM与OB 不垂直,所以C错误,
1 2 1 4 2 1
9 25
对于D,⃗A C=(−4,3,−5),则⃗A C⋅⃗OM=8+ − =0,所以⃗A C⊥⃗OM,所以D正确,
1 1 2 2 1
故选:D.
学科网(北京)股份有限公司2.(2023·全国·高三专题练习)已知点P是正方体ABCD−A B C D 的棱CD的中点,给出以下结论:
1 1 1 1
①A P⊥C D;
1 1
②A P⊥BD;
1
③A P⊥BC ;
1 1
④A P⊥平面BC D
1 1
其中正确命题的序号是( )
A.① B.② C.③ D.④
【解题思路】建立空间直角坐标系,根据空间中两个向量垂直则数量积为0逐个判定即可.
【解答过程】
设正方体边长为2,建立如图空间直角坐标系.则⃑A P=(−2,1,−2).
1
对①, ⃑C D=(0,−2,−2),因为⃑A P⋅⃑C D=0−2+4=2,故①错误.
1 1 1
学科网(北京)股份有限公司对②, ⃑BD=(−2,−2,0),因为⃑A P⋅⃑BD=4−2=2,故②错误.
1
对③, ⃑BC =(−2,0,2),因为⃑A P⋅⃑BD=4−4=0,故③正确.
1 1
对④,由②有A P⊥BD不成立,故A P⊥平面BC D不成立.故④错误.
1 1 1
故选:C.
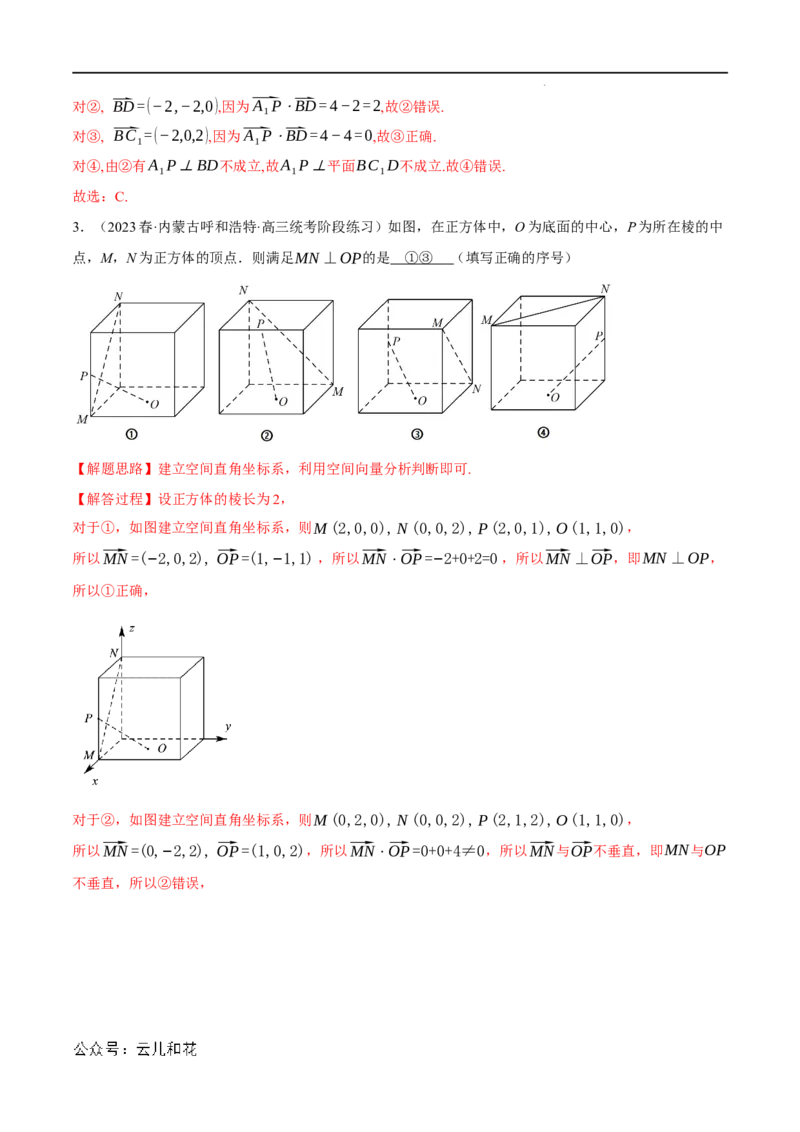
3.(2023春·内蒙古呼和浩特·高三统考阶段练习)如图,在正方体中,O为底面的中心,P为所在棱的中
点,M,N为正方体的顶点.则满足MN⊥OP的是 ①③ (填写正确的序号)
【解题思路】建立空间直角坐标系,利用空间向量分析判断即可.
【解答过程】设正方体的棱长为2,
对于①,如图建立空间直角坐标系,则M(2,0,0),N(0,0,2),P(2,0,1),O(1,1,0),
所以⃗MN=(−2,0,2), ⃗OP=(1,−1,1),所以⃗MN⋅⃗OP=−2+0+2=0,所以⃗MN⊥⃗OP,即MN⊥OP,
所以①正确,
对于②,如图建立空间直角坐标系,则M(0,2,0),N(0,0,2),P(2,1,2),O(1,1,0),
所以⃗MN=(0,−2,2), ⃗OP=(1,0,2),所以⃗MN⋅⃗OP=0+0+4≠0,所以⃗MN与⃗OP不垂直,即MN与OP
不垂直,所以②错误,
学科网(北京)股份有限公司对于③,如图建立空间直角坐标系,则M(2,2,2),N(0,2,0),P(0,0,1),O(1,1,0),
所以⃗MN=(− ⃗O2,P0,=−(−2), ,1,所−以1,⃗1M)N⋅⃗OP=2+0−2=0,所以⃗MN⊥⃗OP,即MN⊥OP,
所以③正确,
对于④,如图建立空间直角坐标系,则M(2,0,2),N(0,2,2),P(0,2,1),O(1,1,0),
所以⃗MN=(−2,2,0), ⃗OP=(−1,1,1),所以⃗MN⋅⃗OP=2+2+0≠0,所以⃗MN与⃗OP不垂直,即MN与
OP不垂直,所以④错误,
故答案为:①③.
4.(2022·全国·高三专题练习)如图,四棱锥P−ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,
∠ABC=60° PA=AB=BC=2,E是PC的中点.
学科网(北京)股份有限公司求证:(1)CD⊥AE;(2)PD⊥平面ABE.
【解题思路】方法一:(1)以A为坐标原点建立空间直角坐标系A−xyz,得到⃗CD、⃗AE,计算得到
⃗CD⋅⃗AE=0,即证明CD⊥AE.
(2)先写出⃗PD坐标,再求出平面ABE的法向量⃗n,验证可知⃗PD//⃗n,即证明PD⊥平面ABE.
方法二:(1)由PA⊥底面ABCD证明PA⊥CD.再结合AC⊥CD可证明CD⊥平面PAC.从而得到
CD⊥AE.
(2)由PA⊥底面ABCD证明PA⊥AB,再结合AB⊥AD证明AB⊥平面PAD,从而得到AB⊥PD;
再证明AE⊥PC.结合CD⊥AE可证AE⊥平面PCD,得到AE⊥PD;最后根据线面垂直的判定即可
以证明PD⊥平面ABE.
【解答过程】方法一 (1)以A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴,建立如图所示
的空间直角坐标系,
( 4√3 ) (1 √3 )
则A(0,0,0),B(2,0,0),C(1,√3,0),D 0, ,0 ,P(0,0,2),E , ,1 ,所以
3 2 2
( √3 ) (1 √3 ) 1 √3 √3
⃗CD= −1, ,0 ,⃗AE= , ,1 ,所以⃗CD⋅⃗AE=−1× + × +0×1=0,所以CD⊥AE.
3 2 2 2 3 2
学科网(北京)股份有限公司( 4√3 ) (1 √3 )
(2)由(1),得⃗PD= 0, ,−2 ,⃗AB=(2,0,0),⃗AE= , ,1 .
3 2 2
2√3
设向量⃗n=(x,y,z)是平面ABE的法向量,则¿,即¿,取y=2,则⃗n=(0,2,−√3),所以⃗PD= ⃗n,所
3
以⃗PD//⃗n,所以PD⊥平面ABE.
方法二 (1)∵PA⊥底面ABCD,∴PA⊥CD.又AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.∵
AE⊂平面PAC,∴CD⊥AE.
(2)∵PA⊥底面ABCD,∴PA⊥AB.又AB⊥AD,PA∩AD=A,∴AB⊥平面PAD,∴
AB⊥PD.由题可得PA=AC=2,由E是PC的中点,∴AE⊥PC.
又CD⊥AE,PC∩CD=C,∴AE⊥平面PCD,∴AE⊥PD.∵AB⊥PD,AE⊥PD,
AB∩AE=A,∴PD⊥平面ABE.
5.(2023秋·湖南娄底·高二校联考期末)如图,在三棱柱 ABC−A B C 中,A A ⊥底面ABC,
1 1 1 1
∠CAB=90∘,AB=AC=2,A A =√3,M 为BC的中点,P 为侧棱 BB 上的动点.
1 1
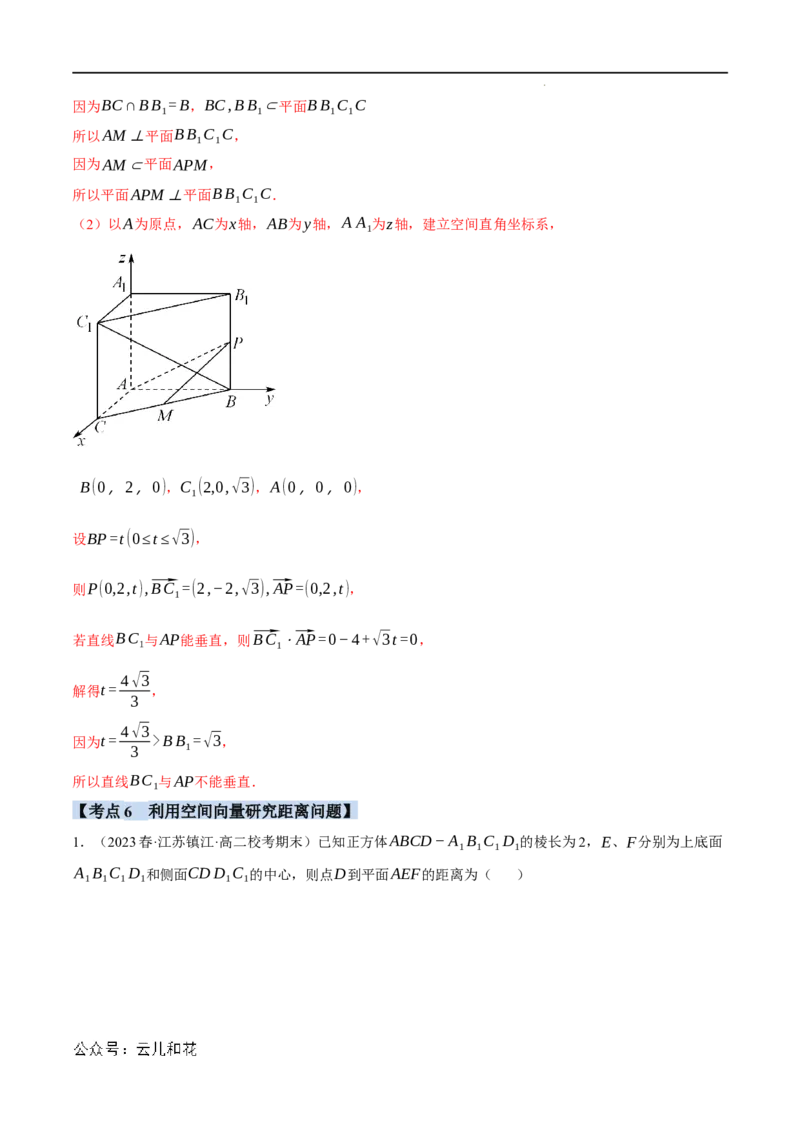
(1)求证:平面APM⊥平面BB C C;
1 1
(2)试判断直线 BC 与AP是否能够垂直.若能垂直,求PB的长;若不能垂直,请说明理由.
1
【解题思路】(1)利用AM⊥BC,AM⊥BB 推出AM⊥平面BB C C,即可证明面面垂直;
1 1 1
(2)建系,写出B,C ,A的坐标,设BP=t(0≤t≤√3),利用直线BC 与AP能垂直,数量积为零,求出
1 1
4√3 4√3
t= ,t= >BB ,不能垂直.
3 3 1
【解答过程】(1)因为在三棱柱 ABC−A B C 中,BB ⊥底面ABC,∠CAB=90∘,AB=AC=2,
1 1 1 1
A A =√3,M 为BC的中点,P 为侧棱 BB 上的动点.
1 1
所以 AM⊥BC,AM⊥BB ,
1
学科网(北京)股份有限公司因为BC∩BB =B,BC,BB ⊂平面BB C C
1 1 1 1
所以AM⊥平面BB C C,
1 1
因为AM⊂平面APM,
所以平面APM⊥平面BB C C.
1 1
(2)以A为原点,AC为x轴,AB为y轴,A A 为z轴,建立空间直角坐标系,
1
B(0,2,0),C (2,0,√3),A(0,0,0),
1
设BP=t(0≤t≤√3),
则P(0,2,t),⃗BC =(2,−2,√3),⃗AP=(0,2,t),
1
若直线BC 与AP能垂直,则⃗BC ⋅⃗AP=0−4+√3t=0,
1 1
4√3
解得t= ,
3
4√3
因为t= >BB =√3,
3 1
所以直线BC 与AP不能垂直.
1
【考点6 利用空间向量研究距离问题】
1.(2023春·江苏镇江·高二校考期末)已知正方体ABCD−A B C D 的棱长为2,E、F分别为上底面
1 1 1 1
A B C D 和侧面CDD C 的中心,则点D到平面AEF的距离为( )
1 1 1 1 1 1
学科网(北京)股份有限公司2√11 √11 √11 4√11
A. B. C. D.
11 11 4 11
【解题思路】建立空间直角坐标系,利用向量法得出点D到平面AEF的距离.
【解答过程】建立如图所示的空间直角坐标系
→
A(0,0,0),E(1,1,2),F(1,2,1),D(0,2,0),⃗AE=(1,1,2),⃗AF=(1,2,1),AD=(0,2,0)
设平面AEF的法向量为⃗n=(x,y,z),¿,令z=−1,得⃗n=(3,−1,−1)
|⃗n⋅⃗AD| 2 2√11
则点D到平面AEF的距离为 = = .
|⃗n| √11 11
故选:A.
2.(2023秋·高二课时练习)正方体ABCD−A B C D 的棱长为1,则平面AB D 与平面BDC 的距
1 1 1 1 1 1 1
离为( )
√2 √3
A.√2 B.√3 C. D.
3 3
【解题思路】将平面AB D 与平面BDC 的距离转化为点B到平面AB D 的距离,建立空间直角坐标
1 1 1 1 1
系,,然后用空间向量求解.
【解答过程】由正方体的性质:AB ∥DC ,D B ∥DB,
1 1 1 1
学科网(北京)股份有限公司AB ∩D B =B ,DC ∩DB=D,
1 1 1 1 1
且AB ⊂平面AB D ,D B ⊂平面AB D ,
1 1 1 1 1 1 1
DC ⊂平面BDC ,DB⊂平面BDC ,
1 1 1
所以平面AB D ∥平面BDC ,
1 1 1
则两平面间的距离可转化为点B到平面AB D 的距离.
1 1
以D为坐标原点,DA,DC,DD 所在的直线分别为x,y,z轴
1
建立空间直角坐标系,如图所示:
由正方体的棱长为1,所以A(1,0,0),B(1,1,0),A (1,0,1),
1
C(0,1,0),B (1,1,1),D (0,0,1)
1 1
所以⃗C A =(1,−1,1),⃗BA=(0,−1,0),
1
⃗AB =(0,1,1),⃗B D =(−1,−1,0).
1 1 1
连接A C,
1
由⃗C A ⋅⃗AB =(1,−1,1)⋅(0,1,1)=1×0+(−1)×1+1×1=0,
1 1
⃗C A ⋅⃗B D =(1,−1,1)⋅(−1,−1,0)=1×(−1)+(−1)×(−1)+1×0=0,
1 1 1
所以⃗C A ⊥⃗AB ⇒C A ⊥AB ,⃗C A ⊥⃗B D ⇒C A ⊥B D ,
1 1 1 1 1 1 1 1 1 1
且AB ∩B D =B ,
1 1 1 1
可知C A ⊥平面AB D ,
1 1 1
得平面AB D 的一个法向量为⃗C A =⃗n=(1,−1,1),
1 1 1
则两平面间的距离:
学科网(北京)股份有限公司|⃗BA⋅⃗n| |0×1+(−1)×(−1)+0×1| 1 √3
d= = = =
.
|⃗n| √12+(−1) 2+12 √3 3
故选:D.
3.(2023·全国·高三专题练习)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,底面ABCD为正方形,
且PA=AB=2,F为棱PD的中点,点M在PA上,且PM=2MA,则CD的中点E到直线MF的距离是
√65
.
5
【解题思路】以点A为坐标原点,AB、AD、AP所在直线分别为x、y、z轴建立空间直角坐标系,计算
出cos∠EFM、sin∠EFM,进而可计算得出点E到直线FM的距离为d=|⃗FE|sin∠EFM.
【解答过程】因为PA⊥平面ABCD,底面ABCD为正方形,
以点A为坐标原点,AB、AD、AP所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系,
( 2)
则点E(1,2,0)、F(0,1,1)、M 0,0, ,
3
2
−
⃗FM= ( 0,−1,− 1) ,⃗FE=(1,1,−1),cos∠EFM= ⃗FM⋅⃗FE = 3 = √30 ,
3 |⃗FM|⋅|⃗FE| √10 15
×√3
3
学科网(北京)股份有限公司√195
所以,sin∠EFM=√1−cos2∠EFM=
,
15
√195 √65
所以,CD的中点E到直线MF的距离d=|⃗FE|sin∠EFM=√3× = .
15 5
√65
故答案为: .
5
4.(2023春·高二单元测试)如图,四棱锥P−ABCD中,底面ABCD为矩形,侧面PAD为正三角形,
AD=2,AB=3,平面PAD⊥平面ABCD,E为棱PB上一点(不与P,B重合),平面ADE交棱PC于点F.
(1)求证:AD//EF;
3√30
(2)若二面角E−AC−B的余弦值为 ,求点B到平面AEC的距离.
20
【解题思路】(1)根据线面平行的判定定理推出AD//平面PBC,再根据线面平行的性质定理可得
AD//EF;
(2)取AD的中点O,连PO,取BC的中点G,连OG,可证PO,AD,OG两两垂直,
以O为原点,OA,OG,OP所在直线为x,y,z轴建立空间直角坐标系,根据题意平面AEC和平面BAC的法
向量,再用点面距公式可求出结果.
【解答过程】(1)因为ABCD为矩形,所以AD//BC,
又AD⊄平面PBC,BC⊂平面PBC,
所以AD//平面PBC,又平面PBC∩平面AEFD=EF,AD在面AEFD内,
所以AD//EF.
(2)取AD的中点O,连PO,取BC的中点G,连OG,则OG⊥AD,
因为侧面PAD为正三角形,所以PO⊥AD,
因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD =AD,PO⊂平面PAD,
所以PO⊥平面ABCD,又OG⊂平面ABCD,所以PO⊥OG,
所以PO,AD,OG两两垂直,
以O为原点,OA,OG,OP所在直线为x,y,z轴建立空间直角坐标系:
学科网(北京)股份有限公司因为AD=2,且侧面PAD为正三角形,所以PO=√3,又AB=3,
所以A(1,0,0),B(1,3,0),C(−1,3,0),P(0,0,√3),⃗AB=(0,3,0),
设⃗PE=t⃗PB,显然t∈(0,1),
所以⃗PB=(1,3,−√3),⃗AP=(−1,0,√3),⃗AC=(−2,3,0),
⃗AE=⃗AP+⃗PE =⃗AP+t⃗PB=(−1,0,√3)+t(1,3,−√3) =(t−1,3t,√3−√3t),
设平面AEC的一个法向量为⃗m=(x,y,z),
√3(3t−1)
则¿,取x=3,则y=2,z= ,
t−1
√3(3t−1)
则⃗m=(3,2, ),
t−1
取平面BAC的一个法向量为⃗n=(0,0,1),
|√3(3t−1)|
|⃗m⋅⃗n| t−1 3√30 3(3t−1) 2 2
则 |cos<⃗m,⃗n>|= = = ,得 =27,解得t= .
|⃗m||⃗n| √ 3(3t−1) 2 20 (t−1) 2 3
9+4+
(t−1) 2
1 √3
所以⃗m=(3,2,−3√3),所以⃗AE=(− ,2, ),⃗BE=⃗AE−⃗AB
3 3
1 √3 1 √3
=(− ,2, )−(0,3,0)=(− ,−1, ),
3 3 3 3
|⃗BE⋅⃗m| |−1−2−3| 3√10
所以点B到平面AEC的距离为 = = .
|⃗m| √9+4+27 10
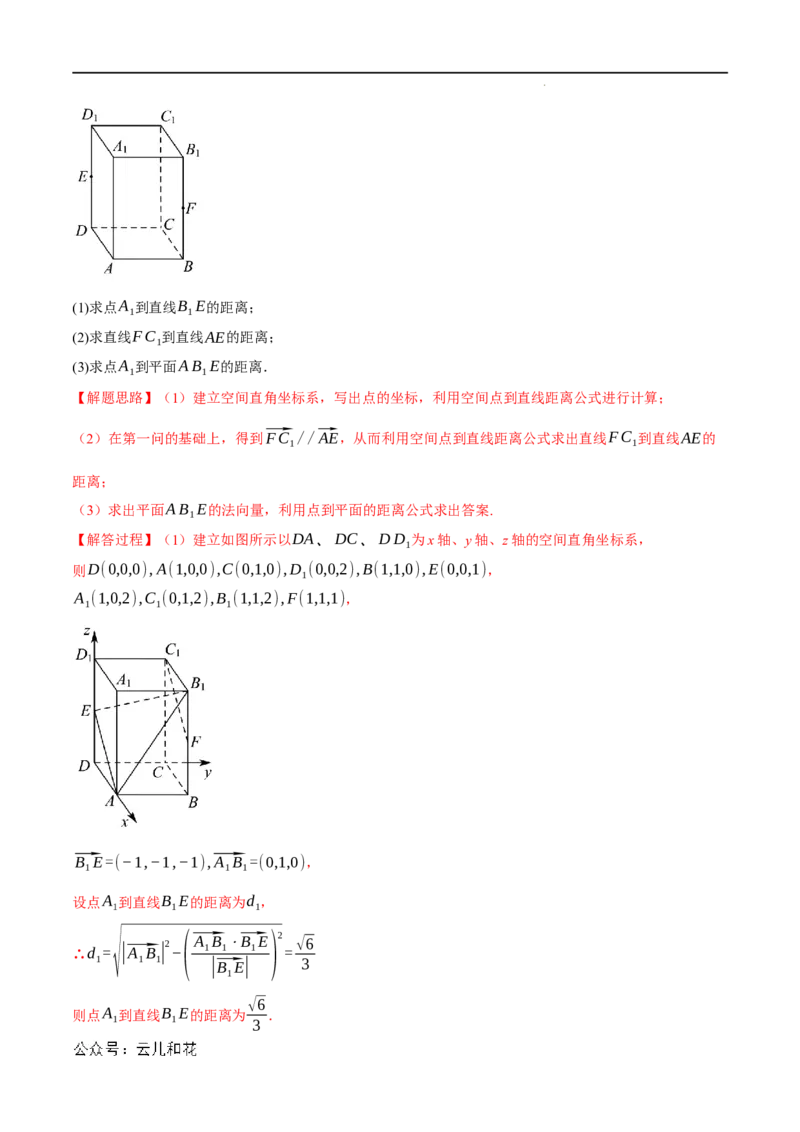
5.(2023春·高二课时练习)如图,在长方体ABCD−A B C D 中,A A=2AB=2BC=2,E为线段
1 1 1 1 1
DD 的中点,F为线段BB 的中点.
1 1
学科网(北京)股份有限公司(1)求点A 到直线B E的距离;
1 1
(2)求直线FC 到直线AE的距离;
1
(3)求点A 到平面AB E的距离.
1 1
【解题思路】(1)建立空间直角坐标系,写出点的坐标,利用空间点到直线距离公式进行计算;
(2)在第一问的基础上,得到⃗FC //⃗AE,从而利用空间点到直线距离公式求出直线FC 到直线AE的
1 1
距离;
(3)求出平面AB E的法向量,利用点到平面的距离公式求出答案.
1
【解答过程】(1)建立如图所示以DA、DC、DD 为x轴、y轴、z轴的空间直角坐标系,
1
则D(0,0,0),A(1,0,0),C(0,1,0),D (0,0,2),B(1,1,0),E(0,0,1),
1
A (1,0,2),C (0,1,2),B (1,1,2),F(1,1,1),
1 1 1
⃗B E=(−1,−1,−1),⃗A B =(0,1,0),
1 1 1
设点A 到直线B E的距离为d ,
1 1 1
∴d = √ |⃗A B | 2 − ( ⃗A 1 B 1 ⋅⃗B 1 E) 2 = √6
1 1 1 |⃗B E| 3
1
√6
则点A 到直线B E的距离为 .
1 1 3
学科网(北京)股份有限公司(2)⃗FC =(−1,0,1),⃗AE=(−1,0,1),故⃗FC //⃗AE
1 1
⃗EF=(1,1,0),
设直线FC 到直线AE的距离为d ,则d 即为F到直线AE的距离;
1 2 2
√ (⃗AE⋅⃗EF) 2 √6
∴d = |⃗EF|2− =
2 |⃗AE| 2
√6
则直线FC 到直线AE的距离为 .
1 2
(3)设平面AB E的法向量为⃗n=(x,y,z),
1
由¿,
令x=1,则y=−2,z=1,所以⃗n=(1,−2,1)
设点A 到平面AB E的距离为d ,
1 1 3
|⃗A B ⋅⃗n| |(0,1,0)⋅(1,−2,1)| √6
∴d = 1 1 = = ,
3 |⃗n| √1+4+1 3
√6
则点A 到平面AB E的距离为 .
1 1 3
【考点7 利用空间向量求空间角】
1.(2023春·重庆沙坪坝·高一校考期末)如图,平行六面体ABCD−A B C D 中,AB=2,AD=3,
1 1 1 1
π
A A =3,∠BAD=∠BA A =∠DA A = ,则B C与BD 所成角的大小为( )
1 1 1 3 1 1
π π π 2π
A. B. C. D.
4 3 2 3
【解题思路】设⃗AB=⃗a,⃗AD=⃗b,⃗A A =⃗c,表示出⃗B C=⃗b−⃗c,⃗BD =⃗b+⃗c−⃗a,计算⃗B C⋅⃗BD =0,
1 1 1 1 1
即可求得答案.
学科网(北京)股份有限公司【解答过程】设⃗AB=⃗a,⃗AD=⃗b,⃗A A =⃗c,则|⃗a|=2,|⃗b|=3,|⃗c|=3,
1
π
三向量⃗AB=⃗a,⃗AD=⃗b,⃗A A =⃗c的夹角皆为 ,
1 3
由题意可得⃗B C=⃗BC−⃗BB =⃗b−⃗c,⃗BD =⃗AD −⃗AB=⃗b+⃗c−⃗a,
1 1 1 1
故⃗B C⋅⃗BD =(⃗b−⃗c)⋅(⃗b+⃗c−⃗a)=⃗b2−⃗b⋅⃗a−⃗c2+⃗a⋅⃗c
1 1
π π
=9−2×3×cos −9+2×3×cos =0,
3 3
π
即⃗B C⊥⃗BD ,所以B C与BD 所成角的大小为 ,
1 1 1 1 2
故选:C.
π
2.(2023·浙江·校联考二模)在平行四边形ABCD中,角A= ,AB=√3,AD=1,将三角形ABD沿BD
6
翻折到三角形A′BD,使平面A′BD⊥平面BCD.记线段A′C的中点为M,那么直线A′D与平面BDM所
成角的正弦值为( )
√6 √3 √2 √3
A. B. C. D.
4 3 2 2
π 2π
【解题思路】由余弦定理,则BD=AD=1,∠DBA=∠A= ,∠ADB= ,以D为原点建立空间直
6 3
角坐标系,利用向量法解决线面角问题.
π
【解答过程】A= ,AB=√3,AD=1,由余弦定理,
6
π
BD2=AB2+AD2−2AB⋅AD⋅cosA=√3 2+12−2×√3×1×cos =1,
6
π 2π
则BD=AD=1,∠DBA=∠A= ,∠ADB=
,
6 3
2π
平面A′BD⊥平面BCD,∠A′DB=∠ADB= ,DC=AB=√3,A′D=AD=BD=1,
3
以D为原点,DB所在直线为y轴,平面ABD内垂直于DB的直线为x轴,垂直于平面ABD的直线为z轴,
学科网(北京)股份有限公司建立如图所示的空间直角坐标系,
则D(0,0,0),A
(√3
,−
1
,0
)
,B(0,1,0),C
(
−
√3
,
3
,0
) ,A′(
0,−
1
,
√3)
,M
(
−
√3
,
1
,
√3)
,
2 2 2 2 2 2 4 2 4
⃗ DA′= ( 0,− 1 , √3) ,⃗DB=(0,1,0),⃗DM= ( − √3 , 1 , √3) ,
2 2 4 2 4
设平面BDM的一个法向量为⃗n=(x,y,z),则有¿,
令x=1,有y=0,z=1,即⃗n=(1,0,1),
√3
cos⃗n, ⃗ DA′=
⃗n⋅ ⃗ DA′
=
2
=
√6
,
|⃗n|⋅
|⃗ DA′| 1×√2 4
√6
所以直线A′D与平面BDM所成角的正弦值为 .
4
故选:A.
3.(2023·全国·高三专题练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多
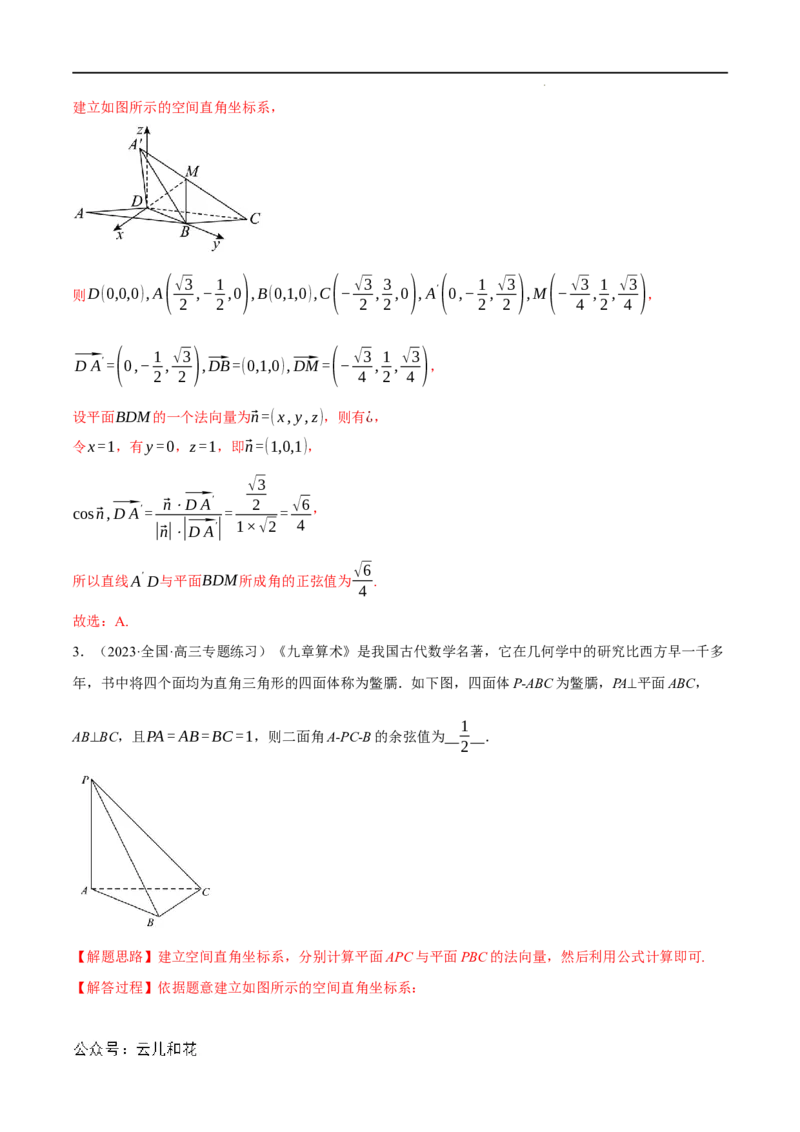
年,书中将四个面均为直角三角形的四面体称为鳖臑.如下图,四面体P-ABC为鳖臑,PA⊥平面ABC,
1
AB⊥BC,且PA=AB=BC=1,则二面角A-PC-B的余弦值为 .
2
【解题思路】建立空间直角坐标系,分别计算平面APC与平面PBC的法向量,然后利用公式计算即可.
【解答过程】依据题意建立如图所示的空间直角坐标系:
学科网(北京)股份有限公司A(0,0,0),B(1,0,0),P(0,0,1),C(1,1,0),
所以⃑AC=(1,1,0),⃑AP=(0,0,1),⃑BC=(0,1,0),⃑PB=(1,0,−1).
设平面APC的法向量为⃑n =(x ,y ,z )
1 1 1 1
¿,∴¿
不妨设y =1,则x =−1,⃑n =(−1,1,0)
1 1 1
设平面PBC的法向量为⃑n =(x ,y ,z )
2 2 2 2
¿,∴¿
不妨设x =1,则z =1,y =0,⃑n =(1,0,1)
2 2 2 2
|⃗n ⋅⃗n | 1 1
设A−PC−B为α,则cosα=|cos⟨⃗n ,⃗n ⟩|= 1 2 = = .
1 2 |⃗n||⃗n | √2⋅√2 2
1 2
1
故答案为: .
2
8√2
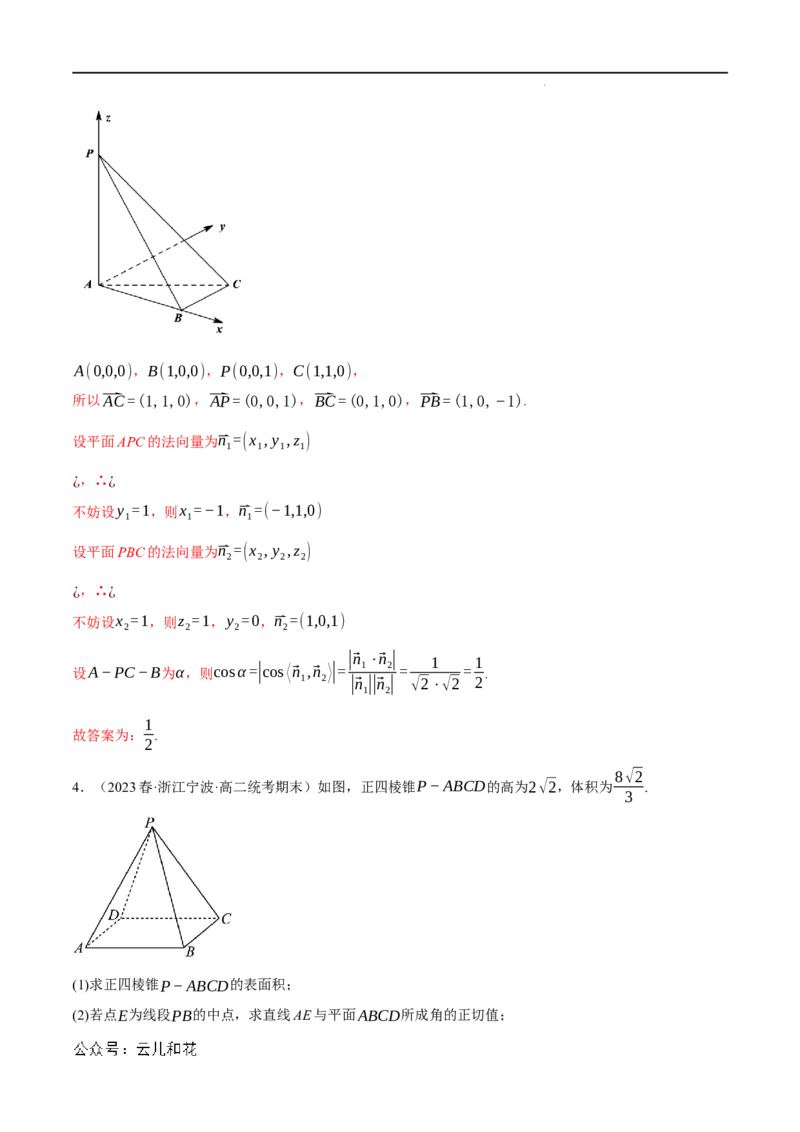
4.(2023春·浙江宁波·高二统考期末)如图,正四棱锥P−ABCD的高为2√2,体积为 .
3
(1)求正四棱锥P−ABCD的表面积;
(2)若点E为线段PB的中点,求直线AE与平面ABCD所成角的正切值;
学科网(北京)股份有限公司(3)求二面角A−PB−C的余弦值.
【解题思路】(1)先由棱锥的体积公式求得底面边长t=2,再利用正四棱锥的性质求得PC,PB,从而求
得S ,进而求得该正四棱锥的表面积;
△PBC
(2)结合(1)中结论建立空间直角坐标系,利用空间向量夹角余弦的坐标表示,结合三角函数的基本关
系式即可得解;
(3)分别求得平面APB与平面PBC的法向量,再利用空间向量夹角余弦的坐标表示即可得解.
【解答过程】(1)连接AC∩BD=O,连接PO,如图,
因为在正四棱锥P−ABCD中,底面ABCD是正方形,则AC⊥BD,且O是AC与BD的中点,PO⊥底
面ABCD,
8√2
因为正四棱锥P−ABCD的高为2√2,体积为 ,则PO=2√2,
3
,设底面ABCD边长为t,则S =t2 ,
ABCD
1 8√2 1
所以由V = S ⋅PO得 = t2×2√2,解得t=2,
P−ABCD 3 ABCD 3 3
因为PO⊥底面ABCD,OC⊂底面ABCD,故PO⊥OC,
1
在Rt△POC中,OC= AC=√2,则PC=√PO2+OC2=√10,同理PB=√10,
2
1
所以在△PBC中,PB=PC=√10,BC=2,则S = ×2×√10−1=3,
△PBC 2
同理:S =S =S =S =3,
△PAB △PAD △PCD △PBC
所以正四棱锥P−ABCD的表面积为S=S +4S =4+4×3=16.
ABCD △PBC
(2)由(1)可得,以O为原点,⃗OA,⃗OB,⃗OP为x,y,z轴,建立空间直角坐标系,如图,
则A(√2,0,0),C(−√2,0,0),B(0,√2,0),D(0,−√2,0),P(0,0,2√2),
学科网(北京)股份有限公司( √2 ) ( √2 )
因为点E为线段PB的中点,所以E 0, ,√2 ,则⃗AE= −√2, ,√2 ,
2 2
易知平面ABCD的一个法向量为⃗n =(0,0,1),
0
π
设直线AE与平面ABCD所成角为θ,则0<θ< ,
2
|⃗AE⋅⃗n |
√2 2
sinθ=|cos⟨⃗AE,⃗n ⟩|= 0 = =
所以 0 |⃗AE||⃗n | √ 1 3,
0 2+ +2×1
2
√5 2 2√5
故cosθ=√1−sin2θ= ,tanθ= = ,
3 √5 5
2√5
所以直线AE与平面ABCD所成角的正切值为 .
5
(3)由(2)知⃗AB=(−√2,√2,0),⃗PB=(0,√2,−2√2),⃗BC=(−√2,−√2,0),
设平面APB的一个法向量为⃗m=(a,b,c),则¿,
取b=2,则a=2,c=1,故⃗m=(2,2,1),
设平面PBC的一个法向量为⃗n=(x,y,z),则¿,
取y=2,则x=−2,z=1,故⃗n=(−2,2,1),
π
设二面角A−PB−C为φ,则由图形可知 <φ<π ,
2
|⃗m⋅⃗n| 1 1
所以cosφ=−|cos⟨⃗m,⃗n⟩|=− =− =− ,
|⃗m||⃗n| √9×√9 9
1
所以二面角A−PB−C的余弦值为− .
9
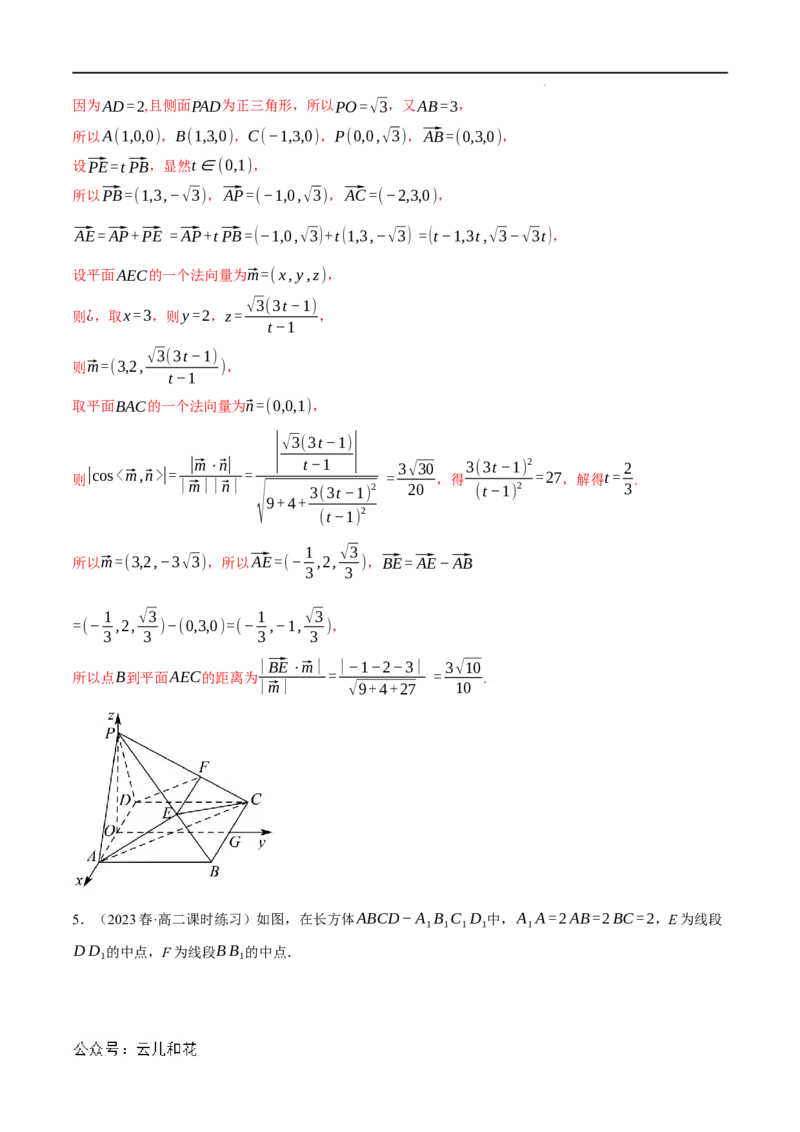
5.(2023春·河南·高三阶段练习)如图,在四棱锥P−ABCD中,底面ABCD是直角梯形,AD⊥CD,
1
AB//CD,AB=2,AD=CD=1,PC⊥底面ABCD,E是AC的中点,⃗PF= ⃗PD.
3
学科网(北京)股份有限公司(1)证明:平面PBC⊥平面ACF.
√10
(2)若直线PE与平面PAB所成角的正弦值为 ,且PC>CD,求平面ACF与平面PAB夹角的余弦值.
15
【解题思路】(1)由余弦定理求出BC2=2,由勾股定理逆定理得到线线垂直,进而得到线面垂直,证明
出面面垂直;
(2)建立空间直角坐标系,设出点的坐标P(0,0,a),利用线面角的大小列出方程,求出a,从而利用空间
向量求出面面角的余弦值
【解答过程】(1)因为PC⊥底面ABCD,AC⊂平面ABCD,所以PC⊥AC.
因为AD=CD=1,AD⊥CD,所以AC=√AD2+CD2=√2,∠CAD=45°.
又AB//CD,AB=2,
所以∠BAC=45°,BC2=AB2+AC2−2AB⋅ACcos∠BAC=2,
则BC2+AC2=AB2,故AC⊥BC.
因为PC∩BC=C,PC,BC⊂平面PBC,所以AC⊥平面PBC.
又AC⊂平面ACF,所以平面PBC⊥平面ACF.
(2)取AB中点N,连接CN,
因为底面ABCD是直角梯形,AD⊥CD,AB//CD,AB=2,AD=CD=1,
所以CN⊥AB,
因为PC⊥底面ABCD,CD,CN⊂平面ABCD,所以PC⊥CN,PC⊥CD,
以C为坐标原点,CN,CD,CP所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
(1 1 )
则A(1,1,0),B(1,−1,0),E , ,0 ,
2 2
( 1 2a)
设P(0,0,a)(a>1),则F 0, , ,
3 3
⃗PE= (1 , 1 ,−a ) ,⃗PA=(1,1,−a),⃗AB=(0,−2,0).
2 2
学科网(北京)股份有限公司设平面PAB的法向量为⃗m=(x ,y ,z ),
1 1 1
则¿,解得y =0,
1
令z =1,得x =a,故⃗m=(a,0,1).
1 1
√10
因为直线PE与平面PAB所成角的正弦值为 ,
15
|1 |
a−a
2 √10
所以 = ,
√ 1 15
a2+ ×√a2+1
2
√2
解得a=2或a= (舍去),则⃗m=(2,0,1),
4
则⃗CA=(1,1,0),⃗CF= ( 0, 1 , 4) .
3 3
设平面ACF的法向量为⃗n=(x ,y ,z ),
2 2 2
则¿,
令z =1,则y =−4,x =4,得⃗n=(4,−4,1).
2 2 2
⃗m⋅⃗n 9 3√165
cos⟨⃗m,⃗n⟩= = = ,
|⃗m||⃗n| √5×√33 55
3√165
故平面ACF与平面PAB夹角的余弦值为 .
55
【考点8 利用空间向量研究存在性问题】
1.(2023·全国·高三专题练习)如图,在多面体ABCDES中,SA⊥平面ABCD,四边形ABCD是正方
形,且DE//SA,SA=AB=2DE,M,N分别是线段BC,SB的中点,Q是线段DC上的一个动点(含端
点D,C),则下列说法正确的是( )
A.存在点Q,使得NQ⊥SB
B.存在点Q,使得异面直线NQ与SA所成的角为60∘
学科网(北京)股份有限公司4
C.三棱锥Q−AMN体积的最大值是
3
D.当点Q自D向C处运动时,二面角N−MQ−A的平面角先变小后变大
【解题思路】以A为坐标原点可建立空间直角坐标系,设Q(m,2,0)(0≤m≤2),根据向量垂直的坐标表
示和异面直线所成角的向量求法可确定m是否有解,从而知AB正误;利用体积桥可知V =V ,
Q−AMN N−AMQ
设DQ=m(0≤m≤2),可求得S 的最大值,由此可求得体积的最大值,知C错误;利用向量法求二面
△AMQ
角余弦关于参数m的表达式,结合二次函数、余弦函数的性质判断二面角的变化情况,判断D.
【解答过程】以A为坐标原点,⃗AB,⃗AD,⃗AS正方向为x,y,z轴,可建立如图所示空间直角坐标系,
设DE=1,则SA=AB=2;
∴A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),E(0,2,1),S(0,0,2),N(1,0,1),M(2,1,0);
对于A,假设存在点Q(m,2,0)(0≤m≤2),使得NQ⊥SB,
则⃗NQ=(m−1,2,−1),又⃗SB=(2,0,−2),
∴⃗NQ⋅⃗SB=2(m−1)+2=0,解得:m=0,
即点Q与D重合时,NQ⊥SB,A正确;
对于B,假设存在点Q(m,2,0)(0≤m≤2),使得异面直线NQ与SA所成的角为60∘,
∵⃗NQ=(m−1,2,−1),⃗SA=(0,0,−2),
|⃗NQ⋅⃗SA| 1 1
∴|cos<⃗NQ,⃗SA>|= = =
,方程无解;
|⃗NQ|⋅|⃗SA| √(m−1) 2+5 2
∴不存在点Q,使得异面直线NQ与SA所成的角为60∘,B错误;
对于C,连接AQ,AM,AN;
学科网(北京)股份有限公司设DQ=m(0≤m≤2),
m
∵S =S −S −S −S =2− ,
△AMQ ▱ABCD △ABM △QCM △ADQ 2
∴当m=0,即点Q与点D重合时,S 取得最大值2;
△AMQ
1
又点N到平面AMQ的距离d= SA=1,
2
1 2
∴(V ) =(V ) = ×2×1= ,C错误;
Q−AMN max N−AMQ max 3 3
对于D,由上分析知:⃗NQ=(m−1,2,−1),⃗NM=(1,1,−1),
⃗m⋅⃗NQ=(m−1)x+2y−z=0
若⃗m=(x,y,z)是面NMQ的法向量,则{ ,
⃗m⋅⃗NM=x+ y−z=0
令x=1,则⃗m=(1,2−m,3−m),
而面AMQ的法向量⃗n=(0,0,1),
⃗m⋅⃗n 3−m
所以 cos<⃗m,⃗n>= = ,令t=3−m∈[1,3],
|⃗m||⃗n| √1+(2−m) 2+(3−m) 2
t 1
cos<⃗m,⃗n>= =
1 1
则 √1+(t−1) 2+t2 √ 1 1 2 3 ,而 ∈[ ,1],
√2⋅ ( − ) + t 3
t 2 4
1
由Q从D到C的过程,m由小变大,则t由大变小,即 由小变大,
t
所以cos<⃗m,⃗n>先变大,后变小,由图知:二面角恒为锐角,
故二面角先变小后变大,D正确.
故选:AD.
2.(2023·全国·高三专题练习)如图,在棱长为1的正方体ABCD−A B C D 中,P为棱BB 的中点,
1 1 1 1 1
Q为正方形BB C C内一动点(含边界),则下列说法中正确的是( )
1 1
A.若D Q//平面A PD,则动点Q的轨迹是一条线段
1 1
学科网(北京)股份有限公司B.存在点Q,使得D Q⊥平面A PD
1 1
C.当且仅当点Q落在C 处时,三棱锥Q−A PD的体积最大
1 1
√6 √2
D.若D Q= ,那么点Q的轨迹长度为 π
1 2 4
【解题思路】选项A:利用面面平行证明线面平行,得到动点轨迹;选项B:利用向量法证明线面垂直,
判断动点是否存在;选项C:利用向量法求点到平面距离,计算棱锥体积;选项D:利用方程判断轨迹形状
并求轨迹长度.
【解答过程】取B C 、C C中点E、F,连接D E、D F、EF、PF,
1 1 1 1 1
由PF//BC //A D 且PF=BC =A D 知A PFD 是平行四边形,∴D F//A P,
1 1 1 1 1 1 1 1 1 1
∵D F⊂平面A PD,A P⊂平面A PD,D F//平面A PD,同理可得EF//平面A PD,
1 1 1 1 1 1 1
∵EF∩D F=F,EF,D F⊂平面D EF,
1 1 1
∴平面A PD//平面D EF,则Q点的轨迹为线段EF,A选项正确;
1 1
如图,建立空间直角坐标系,
( 1)
则A (1,0,0),P 1,1, ,D(0,0,1),设Q(x,1,z),0≤x,z≤1,
1 2
则⃗A D=(−1,0,1),⃗A P= ( 0,1, 1) ,⃗D Q=(x,1,z).
1 1 2 1
设⃗m=(a,b,c)为平面A PD的一个法向量,
1
( 1 )
则¿即¿得¿取c=1,则⃗m= 1,− ,1 .
2
若D Q⊥平面A PD,则⃗D Q//⃗m,即存在λ∈R,使得⃗D Q=λ⃗m,则¿,解得x=z=−2∉[0,1],故
1 1 1 1
不存在点Q使得D Q⊥平面A PD,B选项错误;
1 1
△A PD的面积为定值,∴当且仅当Q到平面A PD的距离d最大时,三棱锥Q−A PD的体积最大.
1 1 1
学科网(北京)股份有限公司d=
|⃗A
1
Q⋅⃗m|
=
2|
x+z−
3|
,
|⃗m| 3 2
3 2
①x+z≤ ,d=1− (x+z),则当x+z=0时,d有最大值1;
2 3
3 2 1
②x+z> ,d= (x+z)−1,则当x+z=2时,d有最大值 ;
2 3 3
综上,当x+z=0,即Q和C 重合时,三棱锥Q−A PD的体积最大,C选项正确;
1 1
√6
D C ⊥平面BB C C,∴D C ⊥C Q,D Q=√D C2+C Q2= ,
1 1 1 1 1 1 1 1 1 1 1 2
√2 √2 π √2
∴C Q= ,Q点的轨迹是半径为 ,圆心角为 的圆弧,轨迹长度为 π,D选项正确.
1 2 2 2 4
故选:ACD.
3.(2023春·江苏常州·高二统考期中)如图,直角梯形ABCD与等腰直角三角形ABP所在的平面互相垂
直,且AB//CD,AB⊥BC,AP⊥PB,AB=2,BC=CD=1.
(1)求证:AB⊥PD;
(2)求直线PC与平面ABP所成角的余弦值;
AE
(3)线段PA上是否存在点E,使得PC//平面EBD?若存在,求出 的值;若不存在,请说明理由.
AP
【解题思路】(1)取AB的中点为O,利用线面垂直的判定、性质推理作答.
(2)以O为原点建立空间直角坐标系,利用空间向量求出线面角的正弦作答.
(3)确定点E的位置,利用空间位置关系的向量证明推理判断作答.
【解答过程】(1)取AB的中点为O,连接DO,PO,由PA=PB,得PO⊥AB,
又四边形ABCD为直角梯形,且AB⊥BC,AB//CD,AB=2,BC=CD=1,
则四边形OBCD为正方形,DO⊥AB,又DO∩PO=O,DO,PO⊂平面POD,
因此AB⊥平面POD,又PD⊂平面POD,
所以AB⊥PD.
学科网(北京)股份有限公司(2)PO⊥AB且PO⊂平面PAB,又平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,
则PO⊥平面ABCD,DO⊂平面ABCD,有PO⊥DO,即有OA,OD,OP两两垂直,
以点O为原点,OD、OA、OP分别为x、y、z轴的空间直角坐标系O−xyz,
由等腰直角△PAB,AB=2,BC=CD=1,得OA=OB=OD=OP=1,
则O(0,0,0),A(0,1,0),B(0,−1,0),C(1,−1,0),D(1,0,0),P(0,0,1),
即⃗PC=(1,−1,−1),平面PAB的一个法向量为⃗OD=(1,0,0),设直线PC与平面PAB所成的角为θ,
|⃗PC⋅⃗OD| √3 √6
因此sinθ=|cos⟨⃗PC,⃗OD⟩|= = ,即cosθ=√1−sin2θ= ,
|⃗PC|⋅|⃗OD| 3 3
√6
所以所求直线PC与平面ABP所成角的余弦值为 .
3
AE 2
(3)线段PA上存在点E,且当 = 时,使得PC//平面EBD.
AP 3
由⃗PE= 1 ⃗PA= ( 0, 1 ,− 1) ,得E ( 0, 1 , 2) ,则⃗EB= ( 0,− 4 ,− 2) ,⃗BD=(1,1,0),
3 3 3 3 3 3 3
设平面EBD的法向量为⃗n=(x,y,z),则¿,令y=−1,得⃗n=(1,−1,2),
又⃗PC⋅⃗n=1×1+(−1)×(−1)+(−1)×2=0,则⃗PC⊥⃗n,而PC⊄平面EBD,因此PC//平面EBD,
AE 2
所以点E满足 = 时,有PC//平面EBD.
AP 3
4.(2023秋·湖南株洲·高三校联考期末)图1是直角梯形ABCD,AB∥CD,∠D=90°,四边形ABCE
是边长为4的菱形,并且∠BCE=60°,以BE为折痕将△BCE折起,使点C到达C 的位置,且
1
AC =2√6,如图2.
1
学科网(北京)股份有限公司(1)求证:平面BC E⊥平面ABED;
1
2√15
(2)在棱DC 上是否存在点P,使得P到平面ABC 的距离为 ?若存在,求出直线EP与平面ABC 所
1 1 5 1
成角的正弦值.
【解题思路】(1)作出辅助线,得到AF⊥BE,C F⊥BE,且AF=C F=2√3,由勾股定理逆定理求出
1 1
AF⊥C F,从而证明出线面垂直,面面垂直;
1
(2)建立空间直角坐标系,利用空间向量求解出点P的坐标,从而得到线面角.
【解答过程】(1)取BE的中点F,连接AF,C F,
1
因为四边形ABCE是边长为4的菱形,并且∠BCE=60°,
所以△ABE,△BEC 均为等边三角形,
1
故AF⊥BE,C F⊥BE,且AF=C F=2√3,
1 1
因为AC =2√6,所以AF2+C F2=AC 2 ,
1 1 1
由勾股定理逆定理得:AF⊥C F,
1
又因为AF∩BE=F,AF,BE⊂平面ABE,
所以C F⊥平面ABED,
1
因为C F⊂平面BEC ,
1 1
所以平面BC E⊥平面ABED;
1
学科网(北京)股份有限公司(2)以F为坐标原点,FA所在直线为x轴,FB所在直线为y轴,FC 所在直线为z轴,建立空间直角坐
1
标系,
则F(0,0,0),A(2√3,0,0),B(0,2,0),C (0,0,2√3),D(√3,−3,0),E(0,−2,0),
1
设P(m,n,t),⃗DP=λ⃗DC ,λ∈[0,1],
1
故(m−√3,n+3,t)=λ(−√3,3,2√3),
解得:m=√3−√3λ,n=3λ−3,t=2√3λ,
故P(√3−√3λ,3λ−3,2√3λ),
设平面ABC 的法向量为⃗v=(x,y,z),
1
则⃗AB=(−2√3,2,0),⃗AC =(−2√3,0,2√3),
1
故¿,
令x=1,则y=√3,z=1,故⃗v=(1,√3,1),
其中⃗C P=(√3−√3λ,3λ−3,2√3λ−2√3)
1
|⃗C P⋅⃗v| |(√3−√3λ,3λ−3,2√3λ−2√3)⋅(1,√3,1)|
2√15
则d= 1 = = ,
|⃗v| √1+3+1 5
1 3
解得:λ= 或 (舍去),
2 2
(√3 3 ) (√3 1 )
则⃗EP= ,− ,√3 −(0,−2,0)= , ,√3 ,
2 2 2 2
设直线EP与平面ABC 所成角为θ,
1
| (√3 1 ) |
, ,√3 ⋅(1,√3,1)
|⃗EP⋅⃗v| 2 2 √15
则sinθ=|cos⟨⃗EP,⃗v⟩|= = = ,
|⃗EP|⋅|⃗v| √3 1 5
+ +3×√1+3+1
4 4
学科网(北京)股份有限公司√15
直线EP与平面ABC 所成角的正弦值为 .
1 5
2π
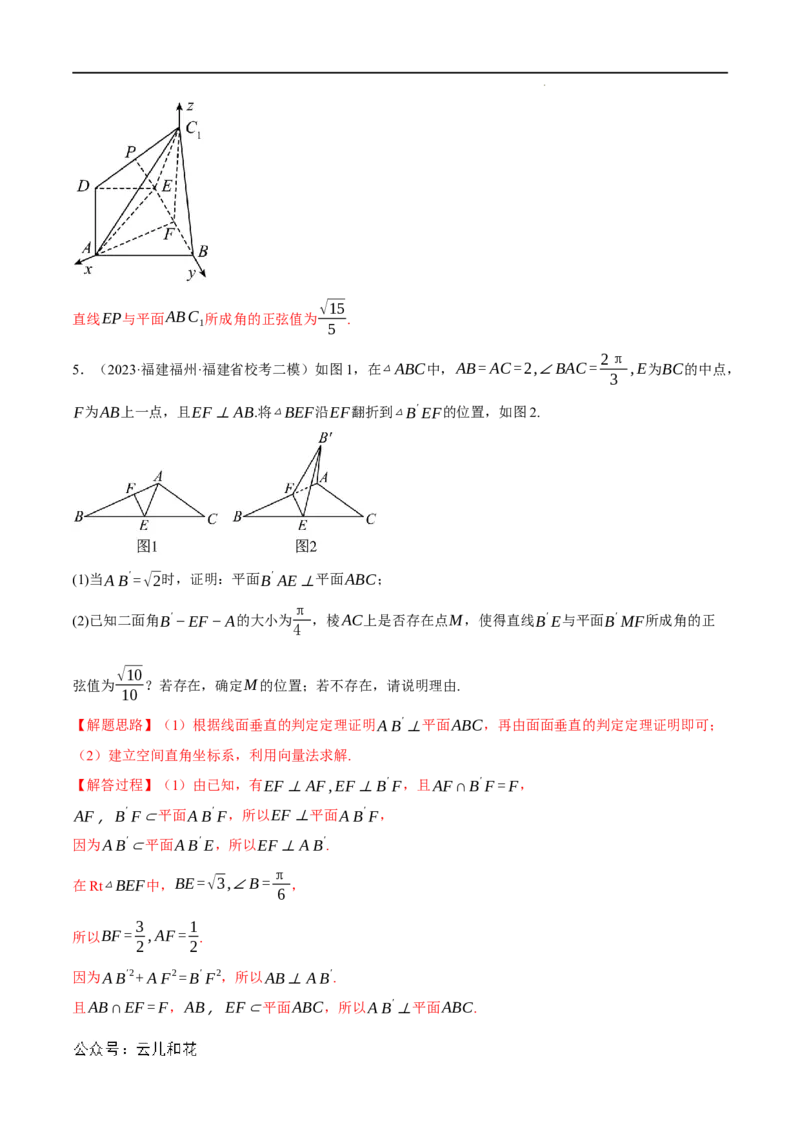
5.(2023·福建福州·福建省校考二模)如图1,在△ABC中,AB=AC=2,∠BAC= ,E为BC的中点,
3
F为AB上一点,且EF⊥AB.将△BEF沿EF翻折到△B′EF的位置,如图2.
(1)当AB′=√2时,证明:平面B′ AE⊥平面ABC;
π
(2)已知二面角B′−EF−A的大小为 ,棱AC上是否存在点M,使得直线B′E与平面B′MF所成角的正
4
√10
弦值为 ?若存在,确定M的位置;若不存在,请说明理由.
10
【解题思路】(1)根据线面垂直的判定定理证明AB′⊥平面ABC,再由面面垂直的判定定理证明即可;
(2)建立空间直角坐标系,利用向量法求解.
【解答过程】(1)由已知,有EF⊥AF,EF⊥B′F,且AF∩B′F=F,
AF,B′F⊂平面AB′F,所以EF⊥平面AB′F,
因为AB′ ⊂平面AB′E,所以EF⊥AB′.
π
在Rt△BEF中,BE=√3,∠B= ,
6
3 1
所以BF= ,AF=
.
2 2
因为AB′2+AF2=B′F2,所以AB⊥AB′.
且AB∩EF=F,AB,EF⊂平面ABC,所以AB′⊥平面ABC.
学科网(北京)股份有限公司因为AB′ ⊂平面AB′E,所以平面AB′E⊥平面ABC.
(2)由(1)EF⊥AF,EF⊥B′F,
π
所以∠AFB′为二面角B′−EF−A的平面角,∠AFB′=
,
4
2π
因为AB=AC=2,∠BAC= ,E为BC的中点,
3
1 3 3 1 √3
所以BE=ABsin60°= BC=√3,BF=B′F=BEcos30°= ,AF=2− = ,EF=BEsin30°= ,
2 2 2 2 2
3√2
B′Fsin45°=B′Fcos45°=
,
4
如图,以F为坐标原点,分别以⃗FB、⃗FE为x轴、y轴正方向建立空间直角坐标系F−xyz.
则F(0,0,0),A
(
−
1
,0,0
)
,C
(
−
3
,√3,0
) ,B′(
−
3√2
,0,
3√2)
,E
(
0,
√3
,0
)
.
2 2 4 4 2
设⃗AM=λ⃗AC,λ∈[0,1],
则⃗FM=⃗FA+⃗AM= ( −λ− 1 ,√3λ,0 ) , ⃗ FB′= ( − 3√2 ,0, 3√2) , ⃗ B′E= (3√2 , √3 ,− 3√2) .
2 4 4 4 2 4
设平面B′MF的一个法向量⃗m=(x,y,z),
由¿,得¿,
2λ+1
(
2λ+1
)
令x=1,则y= ,z=1,所以⃗m= 1, ,1 .
2√3λ 2√3λ
√10
因为直线B′E与平面B′MF所成角的正弦值为 ,
10
| √3 |
(2λ+1)
所以| cos ⟨ ⃗m, ⃗ B′E ⟩| = | ⃗m⋅ ⃗ B′E | = 2 = √10,
|⃗m|⃗ B′E| √3⋅√12λ2+12λ2+(2λ+1) 2 10
1 1
解得λ= 或λ=− (舍).
2 6
学科网(北京)股份有限公司√10
因此,当点M为AC中点时,直线B′E与平面B′MF所成角的正弦值为 .
10
学科网(北京)股份有限公司