文档内容
2024 届高三级 11 月四校联考
数学 答案
简答:1、A 2.D 3.C 4.D 5.A 6.B 7.D 8.C 9. BD 10.ACD 11.BD 12.ABC
21 ( 45)
13.−1 7+4√3 6; 22,
2 2
14. 15. 16.
详解:3.C解:因为y=−ax+4是减函数,且f (x)是R上单调函数,根据题意,f (x)为R上的单调减函数;
{ 00等价于g(x+ )>g(− ),则x+ >− ,解得x>− ,所以不等式
4 2 6 2 6 3
π 1 2π
f(x+ )cos3x− >0的解集为(− ,+∞).故选D.
2 4 3
ωx 1 √3 √3 1 √3 1 √3
8.C解:f(x)=√3sin2 + sinωx− = (1−cosωx)+ sinωx− = sinωx− cosωx
2 2 2 2 2 2 2 2
π π 3π ωπ π π 3ωπ π (π 3π)
=sin(ωx− ),若 0,解得0<ω⩽1,
2 3 2 3 2 ω
ωπ π
{ kπ⩽ −
2 3 2 2 8
又 (k∈Z),解得2k+ ⩽ω⩽ k+ (k∈Z),
3ωπ π 3 3 9
(k+1)π⩾ −
2 3
2 2 8
{2k+ ⩽ k+
3 3 9 4 1
由 (k∈Z),解得− 0
3 9
2 8 2
所以k=0或k=−1,当k=0时, ⩽ω⩽ ,当k=−1时,结合0<ω⩽1,可得0<ω⩽ ,
3 9 9
2 2 8
∴ω∈(0, ]∪[ , ].故选C.
9 3 9
9.BD解:A选项中,a =−2,q=1/3满足{a }单调递增,故A错误;
1 n
a
B选项中,若a >0,00且 n =q∈(0,1),所以{a }单调递减,故B正确;
1 n a n
n−1
1
C选项中,若a =1,q= ,则a 0,ω>0,|φ|< )的部分图象知,
2
11π π 2π
最小正周期T= −(− )=π,∴ω= =2,且A=2. ……………2分
12 12 T
π π π
又(− ,0)在图像上,可得2⋅(− )+φ=kπ,k∈Z,∴φ= +kπ,k∈Z
12 12 6
π π
又∵|φ|< , ∴φ= , ……………4分
2 6
2024届高三级11月四校联考数学答案
第 页,共 页
4 1π
∴f (x)=2sin(2x+ ) ; ……………5分
6
(II)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,
π π
得到y=g(x)=2sin[2(x+θ)+ ]=2sin(2x+2θ+ )的图象, ……………6分
6 6
5π 5π π
若y=g(x)图象的一个对称中心为( ,0),则2· +2θ+ =kπ,k∈Z.……………8分
6 6 6
kπ 11π
即θ= − ,k∈Z ……………9分
2 12
π
∵θ>0,∴取k=2,θ的最小值为 . ……………10分
12
18.解:(1)设数列{a }的公差为d,d≠0,
n
由a =2,且a ,a ,a 成等比数列,可得a2=a a , ……………1分
1 1 3 9 3 1 9
即(2+2d) 2=2(2+8d),解得d=2或d=0(舍去) ……………3分
∴a =2n. ……………4分
n
1 1
(2)由(1)得 − =2n, ……………5分
b b
n n−1
1 1 1 1
∴ − =2(n−1),⋯, − =2×2,
b b b b
n−1 n−2 2 1
1 1 1
将它们累加得: − =n2+n−2, =n2+n. ……………7分
b b b
n 1 n
1
∴b = ,n≥2, ……………8分
n n2+n
1
易知n=1时,b = 也符合上式, ……………9分
1 2
1 1 1 1
所以b = = = − ,n∈N∗, ……………10分
n n2+n n(n+1) n n+1
1 1 1 1 1 1 n
所以S =1− + − +⋯+ − =1− = . ……………12分
n 2 2 3 n n+1 n+1 n+1
2024届高三级11月四校联考数学答案
第 页,共 页
5 1解:(1)证明:取AD的中点O,连接OB,OP,BD, ……………1分
∵19.PA=PD,∴OP⊥AD,∵BD=AB,∴OB⊥AD, ……………2分
又OP∩OB=O,OP、OB⊂平面POB,则AD⊥平面POB, ……………3分
∵PB⊂平面POB,∴AD⊥PB. ……………4分
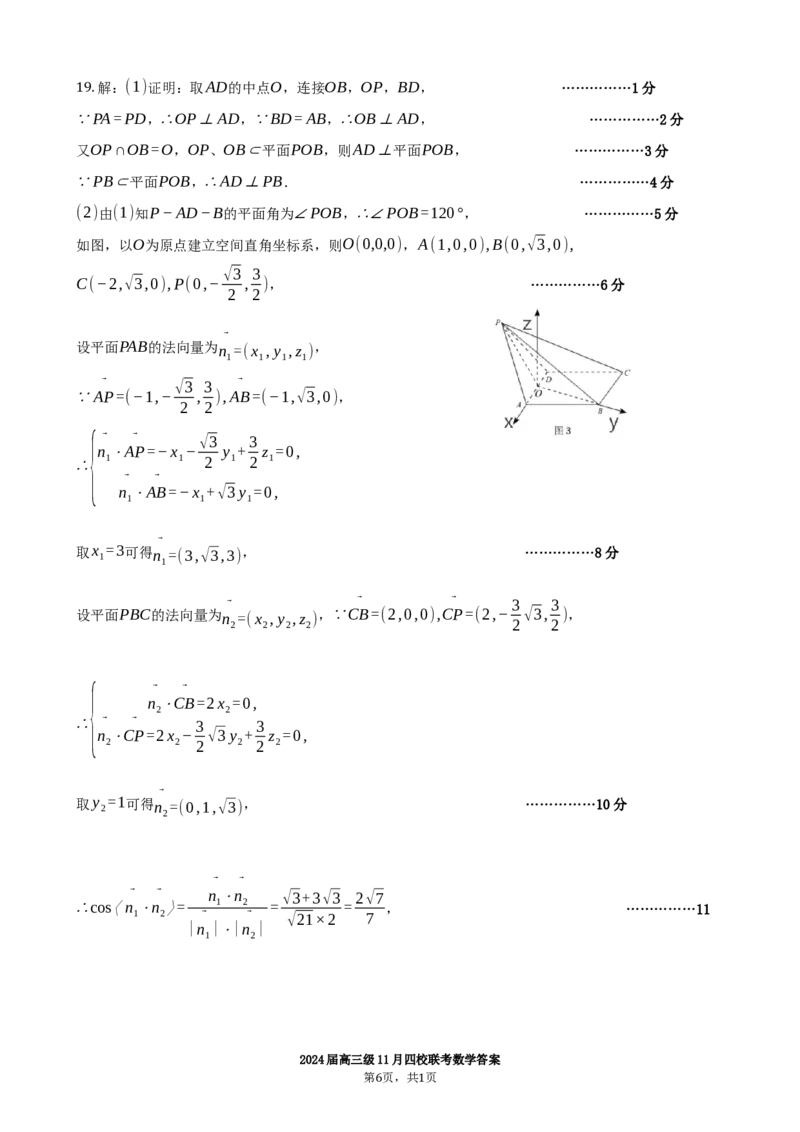
(2)由(1)知P−AD−B的平面角为∠POB,∴∠POB=120°, ……………5分
如图,以O为原点建立空间直角坐标系,则O(0,0,0),A(1,0,0),B(0,√3,0),
√3 3
C(−2,√3,0),P(0,− , ), ……………6分
2 2
⃗
设平面PAB的法向量为n =(x ,y ,z ) ,
1 1 1 1
⃗ √3 3 ⃗
∵AP=(−1,− , ),AB=(−1,√3,0),
2 2
{ ⃗ ⃗ √3 3
n ⋅AP=−x − y + z =0,
∴ 1 1 2 1 2 1
⃗ ⃗
n ⋅AB=−x +√3 y =0,
1 1 1
取x
1
=3可得n ⃗ =(3,√3,3) , ……………8分
1
⃗ ⃗ ⃗ 3 3
设平面PBC的法向量为n =(x ,y ,z ) ,∵CB=(2,0,0),CP=(2,− √3, ),
2 2 2 2 2 2
⃗ ⃗
{
n ⋅CB=2x =0,
2 2
∴ ⃗ ⃗ 3 3
n ⋅CP=2x − √3 y + z =0,
2 2 2 2 2 2
取y
2
=1可得n ⃗ =(0,1,√3) , ……………10分
2
⃗ ⃗
⃗ ⃗ n ⋅n √3+3√3 2√7
∴cos〈n ⋅n 〉= 1 2 = = , ……………11
1 2 ⃗ ⃗ √21×2 7
|n |⋅|n |
1 2
2024届高三级11月四校联考数学答案
第 页,共 页
6 1分
√ (2√7) 2 √21
故二面角A−PB−C的正弦值为 1− = . ……………12分
7 7
解: , , ……………1分
20.
又 函数 在 处的切线平行于 轴,
x
则 ,即 ,解得 ……………2分
此时 ,令 ,解得 ,
当 时 , 单调递增 ……………3分
;
当 时 , 单调递减 ……………4分
.
的单调递增区间为 ,单调递减区间为 ……………5分
令 , , , ……………6分
令 ,得
当 时 , 单调递增当 时 , 单调递减,
;
故 在 处取得极大值 ……………8分
2024届高三级11月四校联考数学答案
第 页,共 页
7 1又 , ……………9分
要使 在 上有两个零点,只需 ,即 , ……………11分
解得 故实数 的取值范围为 ……………12分
a
( π)
21、解:(1)因为线段AA′与线段BC交于点D(异于B,C),所以B,C∈ 0, ,
2
π 2π (π π)
又因为∠BAC= ,所以C= −B∈ , , ……………1
3 3 6 2
分
(√3 )
即tanC∈ ,+∞ , ……………2分
3
(2π )
sin −C
由正弦定理,AC sinB 3 1 √3 ,
= = = +
AB sinC sinC 2 2tanC
……………4分
1 √3 (1 ) AC (1 )
+ ∈ ,2 即 的取值范围为 ,2 . ……………
2 2tanC 2 AB 2
6分
(2)易知AA′=2AD,
1 1
又由三角形ABC的面积S= BC⋅AD= AB⋅AC⋅sin∠BAC,
2 2
√3
可得AD= AB⋅AC, ……………7分
4
由余弦定理,得BC2=4=AB2+AC2−2AB·AC·cos∠BAC≥2AB·AC−AB·AC=AB·AC,…………9
2024届高三级11月四校联考数学答案
第 页,共 页
8 1分
解得AB·AC≤4,当且仅当AB=AC=2时,等号成立, ……………10分
√3
所以AD= AB⋅AC≤√3, ……………11分
4
即AA′的最大值为2√3. ……………12分
AC (1 )
答:(1) 的取值范围为 ,2 ;(2)AA′的最大值为2√3.
AB 2
22.(1)当 时,函数 , ; ………………1分
时, ;
当 时, , ; ………………2分
时,令 ,则 增, ………………3分
存在 ,又 ,
时, , 减,有 , 时, , 增,亦有
,
所以 时,恒有 ,即 ;
即当 时, , ………………5分
又 , ,即当 时, , ……6分
(2)因 ,当 时, , ………………7分
令 , , , ,
2024届高三级11月四校联考数学答案
第 页,共 页
9 1, . ………………8分
又 , ,即当 时, . ………………9分
(3) 由(2)知,当 时,有 当且仅当 时等号成立,
, ……………………10分
则 , ……………………11分
故 . ………………12分
2024届高三级11月四校联考数学答案
第 页,共 页
10 1