文档内容
2025 年 1 月“长沙市联考”考前猜想卷
数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需
改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在
本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共 58 分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知集合A= { x y=ln(1−x)} ,B= { y y=e1−x } ,则AB=( )
A.(−∞,1) B.(0,1) C.(1,+∞) D.∅
【答案】B
【知识点】交集的概念及运算、求指数型复合函数的值域、求对数型复合函数的定义域
【分析】化简集合A,B,结合集合的交集运算定义求结论.
【详解】因为A={ x∣y=ln(1−x)}={x∣x<1},B= { y∣y=e1−x} ={ y∣y>0 },
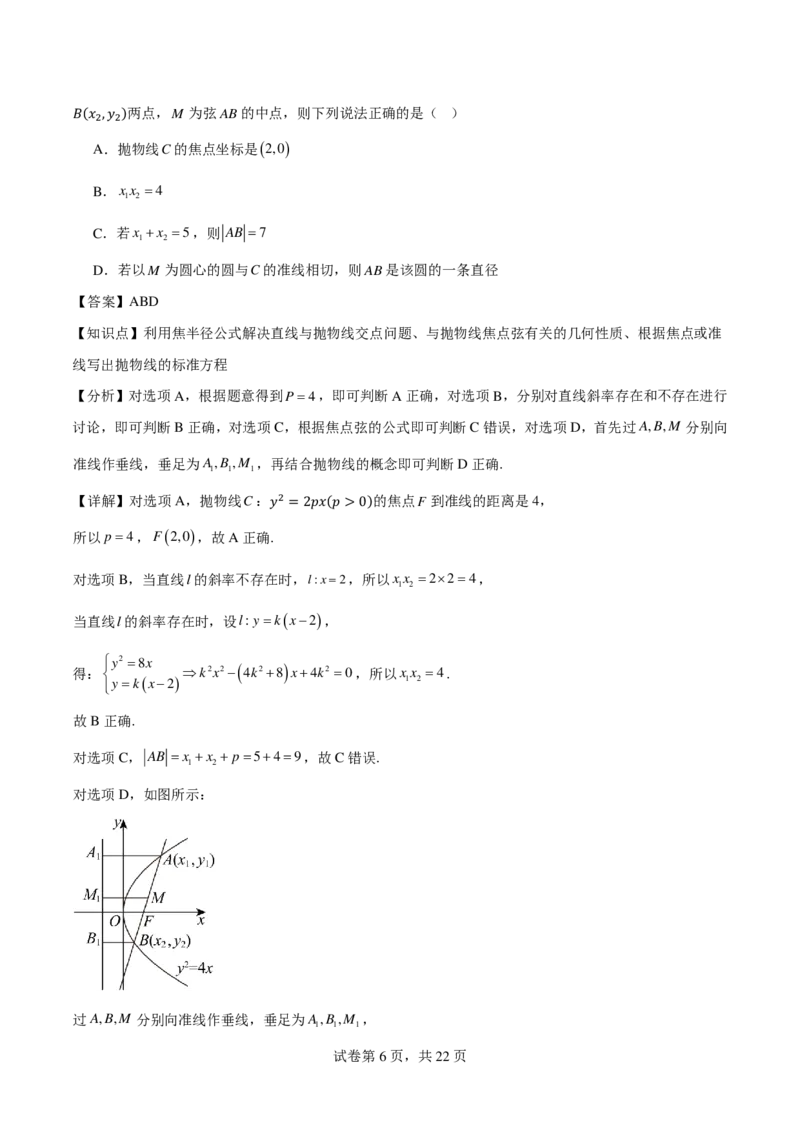
所以A∩B={x∣00) 𝐴𝐴(𝑝𝑝1,𝑦𝑦1)
试卷第5页,共22页
学科网(北京)股份有限公司两点,M 为弦AB的中点,则下列说法正确的是( )
𝐵𝐵(𝑝𝑝 A 2,.𝑦𝑦2 抛 ) 物线C的焦点坐标是(2,0)
B.xx =4
1 2
C.若x +x =5,则 AB =7
1 2
D.若以M 为圆心的圆与C的准线相切,则AB是该圆的一条直径
【答案】ABD
【知识点】利用焦半径公式解决直线与抛物线交点问题、与抛物线焦点弦有关的几何性质、根据焦点或准
线写出抛物线的标准方程
【分析】对选项A,根据题意得到P=4,即可判断A正确,对选项B,分别对直线斜率存在和不存在进行
讨论,即可判断B正确,对选项C,根据焦点弦的公式即可判断C错误,对选项D,首先过A,B,M 分别向
准线作垂线,垂足为A,B,M ,再结合抛物线的概念即可判断D正确.
1 1 1
【详解】对选项A,抛物线C: 的焦点F到准线的距离是4,
2
所以p=4,F(2,0),故A正确𝑦𝑦
.
=2𝑝𝑝𝑝𝑝(𝑝𝑝>0)
对选项B,当直线l的斜率不存在时,l:x=2,所以xx =2×2=4,
1 2
当直线l的斜率存在时,设l:y=k(x−2),
得:
y2 =8x
⇒k2x2− ( 4k2+8 ) x+4k2 =0,所以xx =4.
y=k(x−2) 1 2
故B正确.
对选项C, AB =x +x + p=5+4=9,故C错误.
1 2
对选项D,如图所示:
过A,B,M 分别向准线作垂线,垂足为A,B,M ,
1 1 1
试卷第6页,共22页因为 AA = AF , BB = BF ,
1 1
MM
所以 AB = AF + BF = AA + BB = 1 ,
1 1 2
即:以AB为直径的圆与C的准线相切,故D正确.
故选:ABD
π
10.已知 f (x)=2sin2 ωx+ −1(ω>0),则( )
6
π
A.若 f (x )=1, f (x )=−1,且 x −x = ,则ω=2
1 2 1 2 min 2
π
B.∃ω∈(0,2),使得 f (x)的图象向左平移 个单位长度后所得图象关于原点对称
6
3 π 2π
C.当ω= 时,函数y= f (x)+m(m∈R ),x∈− , 恰有三个零点x、、x x ,且x 0,b>0,
2 1 2 1 2b a 2b a
所以 + = + (a+b)=2+1+ + ≥3+2 ⋅ =3+2 2,
a b a b a b a b
2b a 2 1
当且仅当 = ,即a=2− 2,b= 2−1时等号成立,所以 + 的最小值为3+2 2.
a b a b
故答案为:3+2 2.
4 2
13.已知某家族有A、B两种遗传性状,该家族某位成员出现A性状的概率为 ,出现B性状的概率为 ,
15 15
试卷第10页,共22页7
A、B两种遗传性状都不出现的概率为 .则该成员在出现A性状的条件下,出现B性状的概率为 .
10
3
【答案】
8
【知识点】计算条件概率、利用互斥事件的概率公式求概率、利用对立事件的概率公式求概率
【分析】首先需要定义事件,根据题意得出P(A)和P(B),利用概率公式计算出P(AB),最后根据条件概
率公式计算即可.
【详解】记事件A为该家族某位成员出现A性状;事件B为该家族某位成员出现B性状,由题意得:
P(A)= 4 ,P(B)= 2 ,又P ( A∩B ) = 7 ,
15 15 10
则P(A∪B)=1−P ( A∩B ) =1− 7 = 3 ,且P(A∪B)=P(A)+P(B)−P(AB),
10 10
4 2 3 1 1
则P(AB)=P(A)+P(B)−P(A∪B)= + − = ,因此P(AB)= ,
15 15 10 10 10
1
则P(B|A)=
P(AB)
= 10 = 3 .
P(A) 4 8
15
3
故答案为: .
8
1
14.已知函数 f (x)=lnx+x2−ax有两个极值点m,n,且m∈
,1
,则 f (m)− f (n)的取值范围是
2
3 3
【答案】
ln2− , −ln2
4 4
【知识点】由导数求函数的最值(不含参)、根据极值点求参数
【分析】求 f′(x),根据m,n是 f (x)的两个极值点可得m,n为方程2x2−ax+1=0的两个根,结合韦达定理可
得 f (m)− f (n)=ln ( 2m2) −m2+ 1 ,令t=m2,构造函数g(t)分析单调性可得g(t)的值域,即得
4m2
f (m)− f (n)的取值范围.
【详解】∵ f (x)=lnx+x2−ax,∴ f′(x)= 1 +2x−a= 2x2−ax+1 ,
x x
∴m,n为方程2x2−ax+1=0的两个根,
1 a 1 1
∴mn= ,m+n= ,∴n= ,a=2(m+n)=2m+ ,
2 2 2m m
m
∴ f (m)− f (n)=lnm+m2−am−lnn−n2+an=ln +m2−n2−a(m−n)
n
=ln m +m2−n2−2(m+n)(m−n)=ln m − ( m2−n2)
n n
试卷第11页,共22页
学科网(北京)股份有限公司代入n= 1 可得: f (m)− f (n)=ln ( 2m2) −m2+ 1 ,
2m 4m2
1 1
设t=m2,∵m∈
,1
,∴t∈
,1
,
2 4
设g(t)=ln2t−t+ 1 ,则 g′(t)= 1 −1− 1 = −(2t−1)2 ≤0 ,
4t t 4t2 4t2
1
∴g(t)在
,1
上单调递减,
4
1 3 3
∵g = −ln2,g(1)=ln2− ,
4 4 4
3 3 3 3
∴g(t)∈ ln2− , −ln2 ,即 f (m)− f (n)的取值范围是 ln2− , −ln2 .
4 4 4 4
3 3
故答案为: ln2− , −ln2 .
4 4
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
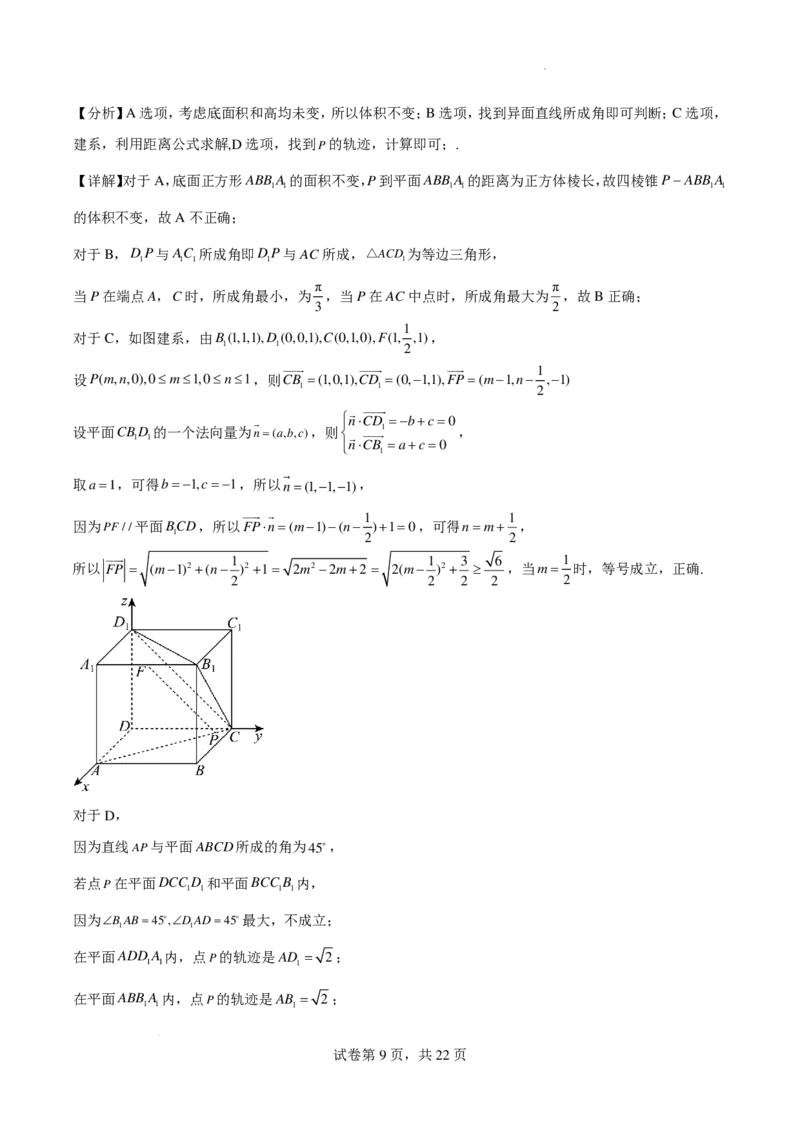
15.如图PA⊥平面ABCD,PA= AC =4,BC =2,AB=2 3.
(1)若AD//平面PBC,证明:AD⊥PB;
π
(2)若AD=2,∠ACD= ,求平面PBD和平面PDC夹角的余弦值.
6
【答案】(1)证明过程见解析;
285
(2) .
19
【知识点】证明线面垂直、面面角的向量求法、线面垂直证明线线垂直、线面平行的性质
【分析】(1)由勾股定理逆定理得到BC⊥AB,由线面垂直得到PA⊥BC,从而证明出线面垂直,得到BC
⊥PB,再由线面平行的性质得到AD//BC,证明出结论;
(2)建立空间直角坐标系,求出所需点的坐标和向量坐标,求出两个平面的法向量,利用法向量的夹角余
弦公式即可求出面面角的夹角余弦值.
【详解】(1)因为AC =4,BC =2,AB=2 3,故BC2+ AB2 = AC2,
试卷第12页,共22页所以BC⊥AB,
又PA⊥平面ABCD,BC⊂平面ABCD,
所以PA⊥BC,
因为ABPA= A,AB,PA⊂平面APB,
所以BC⊥平面APB,
因为PB⊂平面APB,
所以BC⊥PB,
因为AD//平面PBC,AD⊂平面ABCD,平面ABCD ∩平面PBC=BC,
所以AD//BC,
因为BC⊥PB,
所以AD⊥PB;
1 π
(2)由(1)知,BC⊥AB,又BC = AC,故∠CAB= ,
2 6
π
因为AD=2,∠ACD= ,
6
CD2+AC2−AD2
在ACD中,由余弦定理得cos∠ACD= ,
2CD⋅AC
CD2+42−22 3
即 = ,解得CD=2 3,
2CD⋅4 2
因为CD2+AD2 = AC2,所以CD⊥AD,
3 1
过点D作DH ⊥AC于点H,则DH = AD= 3,AH = AD=1,
2 2
以A为坐标原点,AC,AP所在直线分别为y,z轴,建立如图所示的空间直角坐标系,
则D ( − 3,1,0 ) ,B ( 3,3,0 ) ,P(0,0,4),C(0,4,0),
( ) ( )
故PB= 3,3,−4 ,PD= − 3,1,−4 ,PC=(0,4,−4),
设平面PBD的法向量为m=(x,y,z),
试卷第13页,共22页
学科网(北京)股份有限公司 m ⊥ P B m ⋅ P B =(x,y,z)⋅ ( 3,3,−4 ) = 3x+3y−4z=0
则 m ⊥ P D ,所以 m ⋅ P D =(x,y,z)⋅ ( − 3,1,−4 ) =− 3x+y−4z=0 ,
2 3 2 3
令y=2,则z=1,x=− ,故m=
− ,2,1
,
3 3
设平面PDC的法向量为n=(a,b,c),
n⋅PC =(a,b,c)⋅(0,4,−4)=4b−4c=0
则 m ⋅ P D =(a,b,c)⋅ ( − 3,1,−4 ) =− 3a+b−4c=0 ,
( )
令b=1,则c=1,a=− 3,则n= − 3,1,1 ,
设平面PBD和平面PDC夹角为θ,
2 3 ( )
− ,2,1⋅ − 3,1,1
m⋅n 3 285
则 cosθ= cos m,n = = = .
m⋅ n 4 19
+4+1× 3+1+1
3
16.为进一步提升人才选拔的公正性,某省拟在三年内实现高考使用新高考全国Ⅰ卷,为测试学生对新高考
试卷的适应性,特此举办了一次全省高三年级数学模拟考试(满分150分),其中甲市有10000名学生参加
考试.根据成绩反馈,该省及各市本次模拟考试成绩X都近似服从正态分布N
( µ,σ2)
.
(1)已知本次模拟考试甲市平均成绩为97.5分,成绩位于(97.5,130.5]区间内的学生共有4772人.甲市学生A
的成绩为114分,试估计学生A在甲市的大致名次;
(2)在参加该省本次模拟考试的学生中随机抽取500人作为研究样本,随机变量Y为本次考试数学成绩在
(µ−3σ,150]之外的人数,求P(Y ≥1)的概率及随机变量Y的数学期望.
附:参考数据:0.9987500 ≈0.5218,0.9987499 ≈0.5225
参考公式:若X ∼N
( µ,σ2)
,有P(µ−σ< X <µ+σ)=0.6826,P(µ−2σ< X <µ+2σ)=0.9544,
P(µ−3σ< X <µ+3σ)=0.9974.
【答案】(1)1587名
(2)0.0013,0.65
【知识点】二项分布的均值、指定区间的概率、正态分布的实际应用
【分析】(1)考试成绩X 近似服从正态分布N
( µ,σ2)
,根据概率公式计算出概率后可得名次;
(2)求出事件B:在样本中抽取的学生在本次考试中数学成绩在(µ−3σ,150]之外的概率,随机变量Y服从
试卷第14页,共22页二项分布,即Y ∼B(500,0.0013),由公式P(Y ≥1)=1−P(Y =0)计算出概率,再由二项分布的期望公式计算
出期望.
【详解】(1)已知本次模拟考试成绩X 近似服从正态分布N
( µ,σ2)
,
由题意可得µ=97.5,
4772 P(µ−2σ< X <µ+2σ)
=0.4772= ,,
10000 2
∴µ+2σ=130.5,即97.5+2σ=130.5,解得σ=16.5,
甲市学生A在该次考试中成绩为114分,且114=µ+σ,
1−P(µ−σ< X <µ+σ)
又 =0.1587,即P(X ≥µ+σ)=0.1587,
2
∴10000×1587=1587,
答:学生A在甲市本次考试的大致名次为1587名.
(2)设事件B:在样本中抽取的学生在本次考试中数学成绩在(µ−3σ,150]之外,
由于成绩在(µ−3σ,µ+3σ)之内的概率为0,9974,
0.9974
∴P(B)=0.5− =0.0013,
2
∴随机变量Y服从二项分布,即Y ∼B(500,0.0013),
∴P(Y ≥1)=1−P(Y =0)=1−0.9987500 ≈1−0.5218=0.4782,
Y的数学期望为E(Y)=np=500×0.0013=0.65.
17.已知函数 f (x)=(x−2)( ex−ax ) ,a∈R.
(1)求函数y= f (x)的图象经过的所有的定点坐标,并写出函数y= f (x)的一条以上述一个定点为切点的切
线;
(2)讨论函数y= f (x)的单调性;
(3)当a=0时,证明: f (x+2)(lnx+x−1)+e2 ≥0.
【答案】(1)y= ( e2−2a ) (x−2)(或y =(2a−1)x−2)
(2)答案见详解
(3)证明见详解
【知识点】利用导数证明不等式、含参分类讨论求函数的单调区间、求在曲线上一点处的切线方程(斜率)
试卷第15页,共22页
学科网(北京)股份有限公司【分析】(1)分析可知定点的坐标为(2,0)和(0,−2),求导,根据导数的几何意义求切线方程;
(2)求导,分类讨论a的符号,和两根大小,利用导数判断原函数单调性;
(3)分析可知原不等式等价于ex( xlnx+x2−x ) +1≥0,构建函数g(x)=ex( xlnx+x2−x ) +1,利用导数结
合最值分析证明.
【详解】(1)因为 f (2)=0, f (0)=−2,其他函数值均与a有关,
所以 f(x)的图象经过的所有定点的坐标为(2,0)和(0,−2),
又因为 f′(x)=ex−ax+(x−2) ( ex−a ) =(x−1) ( ex−2a ) ,
若以(2,0)为切点,则切线斜率为 f′(2)=e2−2a,切线方程为y= ( e2−2a ) (x−2);
若以(0,−2)为切点,则切线斜率为 f′(0)=2a−1,切线为y =(2a−1)x−2;
所以切线方程为y= ( e2−2a ) (x−2)(或y =(2a−1)x−2).
(2)因为 f′(x)=(x−1) ( ex−2a ) ,
①当a≤0时,ex −2a>0恒成立,
所以当x<1时, f′(x)<0, f(x)在(−∞,1)单调递减,
当x>1时, f′(x)>0, f(x)在(1,+∞)单调递增;
②当a>0时,由 f′(x)=0,得x =1或x =ln(2a).
1 2
e
当ln(2a)=1,即a= 时, f′(x)≥0恒成立,则 f(x)在R上单调递增,
2
e
当ln(2a)>1时,即a> 时,当x<1时, f′(x)>0, f(x)在(−∞,1)单调递增;
2
当1ln(2a)时, f′(x)>0, f(x)在(ln(2a),+∞)单调递增;
e
当ln(2a)<1时,即00, f(x)在(−∞,ln(2a))单调递增;
当ln(2a)< x<1时, f′(x)<0, f(x)在(ln(2a),1)单调递减;
当x>1时, f′(x)>0, f(x)在(1,+∞)单调递增;
综上所述:当a≤0时, f(x)在(−∞,1)单调递减,在(1,+∞)单调递增;
e
当0 时, f(x)在(−∞,1)单调递增,在(1,ln(2a))单调递减,在(ln(2a),+∞)单调递增.
2
(3)当a=0时, f(x+2)(lnx+x−1)+e2 ≥0⇔ex( xlnx+x2−x ) +1≥0.
令g(x)=ex( xlnx+x2−x ) +1,则g′(x)=ex( xlnx+x2−x+lnx+1+2x−1 ) =ex(x+1)(lnx+x)
1
令h(x)=lnx+x,h′(x)= +1,则h(x)在(0,+∞)上单调递增.
x
1 1
又因为h(1)=1>0,h =−1+ <0,
e e
1 1
所以存在t∈ ,1,使得h(t)=lnt+t =0,即lnt =−t,即et = .
e t
当x∈(0,t)时,h(x)<0,g′(x)<0,g(x)单调递减;
当x∈(t,+∞)时,h(x)>0,g′(x)>0,g(x)单调递增.
所以g(x)≥g(t)=et( tlnt+t2−t ) +1=0.
所以ex( xlnx+x2−x ) +1≥0也即 f(x+2)(lnx+x−1)+e2 ≥0.
【点睛】方法点睛:利用导数证明不等式的基本步骤
(1)作差或变形;
(2)构造新的函数h(x);
(3)利用导数研究h(x)的单调性或最值;
(4)根据单调性及最值,得到所证不等式.
特别地:当作差或变形构造的新函数不能利用导数求解时,一般转化为分别求左、右两端两个函数的最值
问题.
x2 y2 1
18.已知椭圆Γ: + =1(a>b>0)的左、右焦点分别为F,F ,离心率e= ,点D在椭圆上,且DF ⋅FF =0,
a2 b2 1 2 2 1 1 2
3
DF = .
1 2
(1)求椭圆Γ的方程;
(2)过点F的动直线l与椭圆Γ交于A,B两点(不与椭圆的左、右顶点重合).
1
π
①当l的倾斜角为 时,求△ABF 的面积;
3 2
②点P为椭圆Γ的右顶点,直线PA、PB分别与y轴相交于点M、N,求证以MN为直径的圆被x轴截得的
弦长为定值.
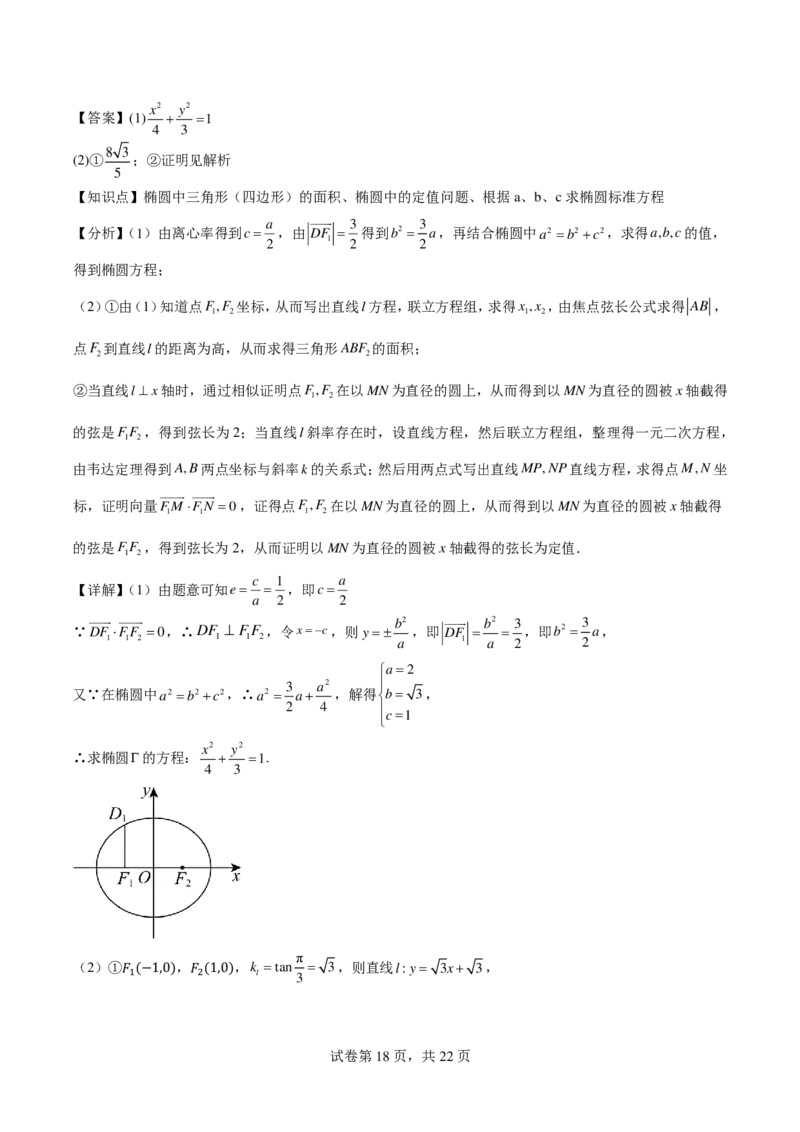
试卷第17页,共22页
学科网(北京)股份有限公司x2 y2
【答案】(1) + =1
4 3
8 3
(2)① ;②证明见解析
5
【知识点】椭圆中三角形(四边形)的面积、椭圆中的定值问题、根据a、b、c求椭圆标准方程
a 3 3
【分析】(1)由离心率得到c= ,由 DF = 得到b2 = a,再结合椭圆中a2 =b2+c2,求得a,b,c的值,
2 1 2 2
得到椭圆方程;
(2)①由(1)知道点F,F 坐标,从而写出直线l方程,联立方程组,求得x,x ,由焦点弦长公式求得 AB ,
1 2 1 2
点F 到直线l的距离为高,从而求得三角形ABF 的面积;
2 2
②当直线l⊥x轴时,通过相似证明点F,F 在以MN为直径的圆上,从而得到以MN为直径的圆被x轴截得
1 2
的弦是FF ,得到弦长为2;当直线l斜率存在时,设直线方程,然后联立方程组,整理得一元二次方程,
1 2
由韦达定理得到A,B两点坐标与斜率k的关系式;然后用两点式写出直线MP,NP直线方程,求得点M,N坐
标,证明向量FM⋅FN =0,证得点F,F 在以MN为直径的圆上,从而得到以MN为直径的圆被x轴截得
1 1 1 2
的弦是FF ,得到弦长为2,从而证明以MN为直径的圆被x轴截得的弦长为定值.
1 2
c 1 a
【详解】(1)由题意可知e= = ,即c=
a 2 2
b2 b2 3 3
∵DF ⋅FF =0,∴DF ⊥ FF ,令x=−c,则y=± ,即 DF = = ,即b2 = a,
1 1 2 1 1 2 a 1 a 2 2
a=2
3 a2
又∵在椭圆中a2 =b2+c2,∴a2 = a+ ,解得b= 3,
2 4
c=1
x2 y2
∴求椭圆Γ的方程: + =1.
4 3
π
(2)① , ,k =tan = 3,则直线l:y= 3x+ 3,
l 3
𝐹𝐹1(−1,0) 𝐹𝐹2(1,0)
试卷第18页,共22页y= 3x+ 3
8
联立方程组
x2
+
y2
=1
,解得x
1
=−
5
,x
2
=0,
4 3
( )2 8 16
焦点弦长 AB = 1+ 3 x −x =2× = ,
1 2 5 5
3−0+ 3
点F 到直线l的距离d = = 3,
2 ( )2
1+ 3
1 8 3
∴S = AB ⋅d =
ABF2
2 5
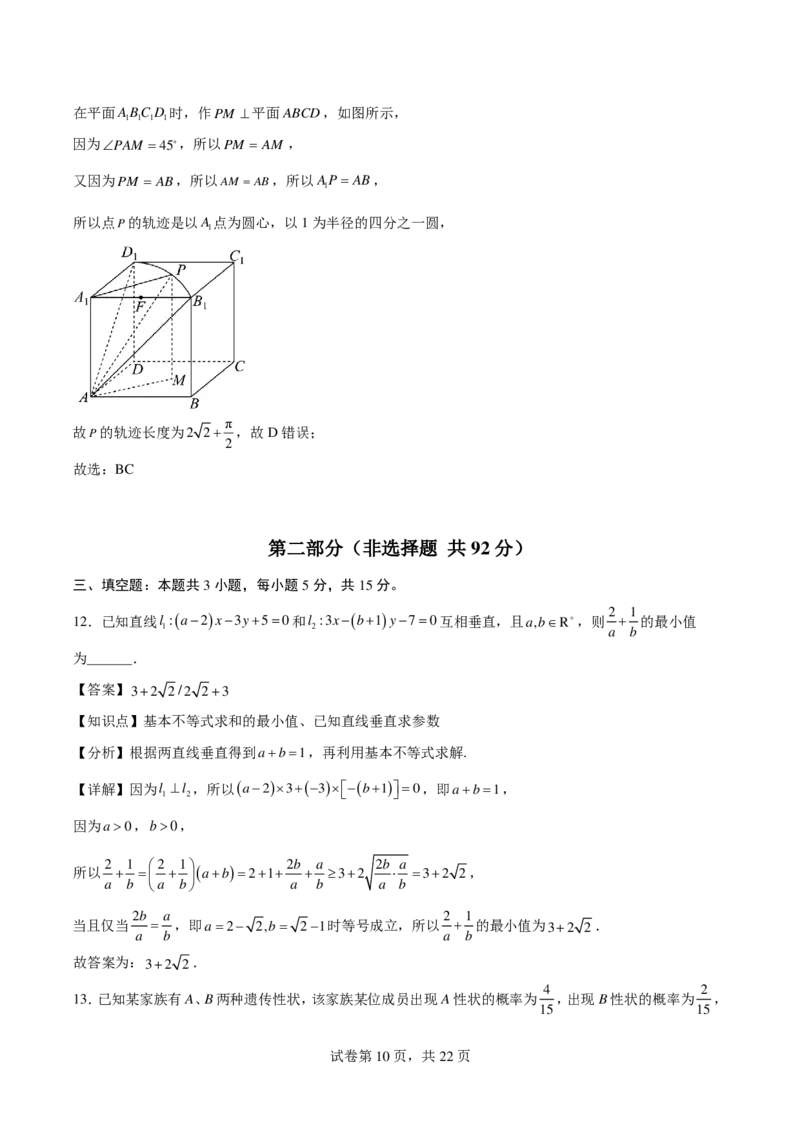
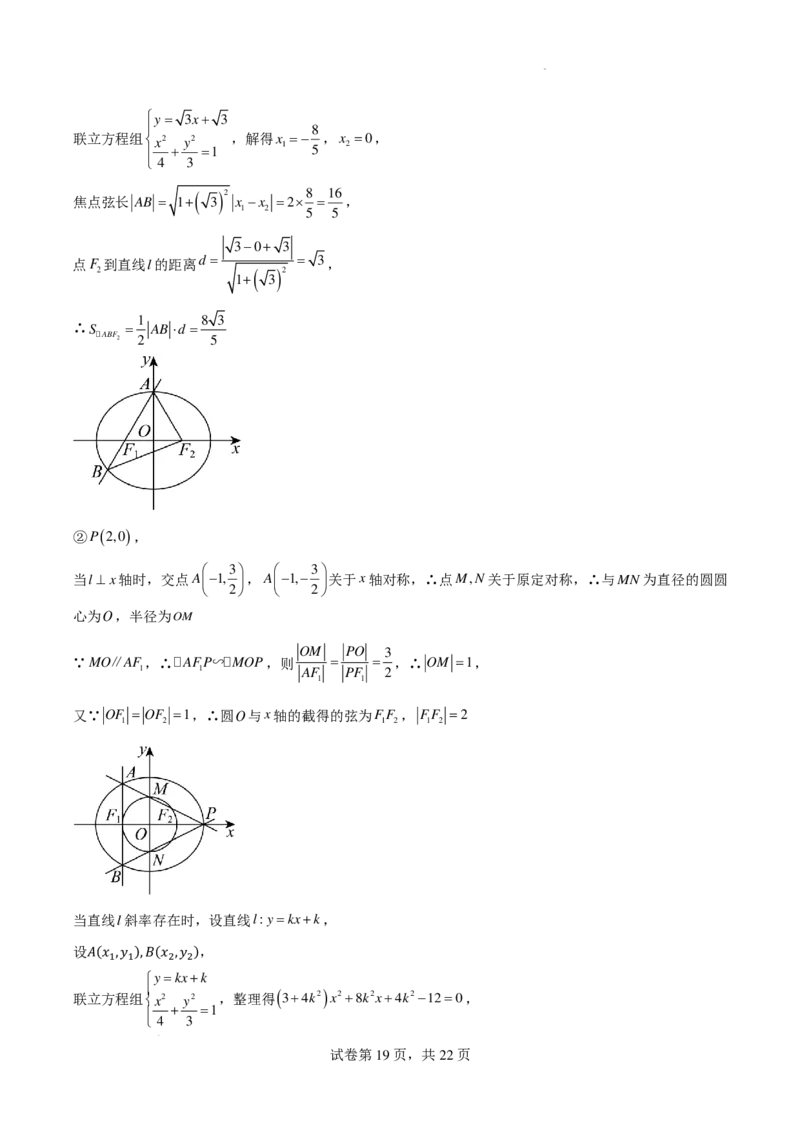
②P(2,0),
3 3
当l⊥x轴时,交点A−1, ,A−1,− 关于x轴对称,∴点M,N关于原定对称,∴与MN为直径的圆圆
2 2
心为O,半径为OM
OM PO 3
∵MO∥AF,∴AFP∽MOP,则 = = ,∴OM =1,
1 1 AF PF 2
1 1
又∵OF = OF =1,∴圆O与x轴的截得的弦为FF , FF =2
1 2 1 2 1 2
当直线l斜率存在时,设直线l:y=kx+k,
设 ,
𝐴𝐴(𝑝𝑝1,𝑦𝑦1),𝐵𝐵 y (𝑝𝑝 =2, k 𝑦𝑦 x2+ ) k
联立方程组 x2 y2 ,整理得 ( 3+4k2) x2+8k2x+4k2−12=0,
+ =1
4 3
试卷第19页,共22页
学科网(北京)股份有限公司8k2 4k2−12
则x +x =− ,xx = ,
1 2 3+4k2 1 2 3+4k2
−9k2
y y =k2(xx +x +x +1)= ,
1 2 1 2 1 2 3+4k2
y−y x−x 2y 2y
直线PM : 1 = 1 ,令x=0,则y= 1 ,M0, 1
0−y 1 2−x 1 2−x 1 2−x 1
y−y x−x 2y 2y
直线PN: 2 = 2 ,令x=0,则y= 2 ,N0, 2
0−y 2 2−x 2 2−x 2 2−x 2
2y 2y
则FM =1, 1 ,FN =1, 2 ,
1 2−x 1 2−x
1 2
2y 2y 4y y
则FM⋅FN =1+ 2 ⋅ 1 =1+ 1 2
1 1 2−x 2−x 4−2(x +x )+xx
2 1 1 2 1 2
−9k2
4× 3+4k2 −36k2
即F
1
M⋅F
1
N =1+
8k2 4k2−12
=1+
12+16k2+16k2+4k2−12
=1−1=0
4−2− +
3+4k2
3+4k2
即FM ⊥FN,同理可证FM ⊥F N ,
1 1 2 2
即点F,F 在以MN为直径的圆上,又∵F,F 在x轴上,
1 2 1 2
∴以MN为直径的圆被x轴截得的弦为FF , FF =2,
1 2 1 2
综上所述:以MN为直径的圆被x轴截得的弦长为定值2.
(a +a ++a )−a
19.已知项数为m(m∈N*,m≥2)的数列{a }为递增数列,且满足a ∈N*,若b = 1 2 m n ,
n n n m−1
且b ∈N*,则称{b }为{a }的“伴随数列”.
n n n
(1)数列4,10,16,19是否存在“伴随数列”,若存在,写出其“伴随数列”,若不存在,说明理由;
(2)若{b }为{a }的“伴随数列”,证明:b >b >>b ;
n n 1 2 m
(3)已知数列{a }存在“伴随数列” {b },且a =1,a =2025,求m的最大值.
n n 1 m
试卷第20页,共22页【答案】(1)存在,“伴随数列”是15,13,11,10
(2)见解析
(3)m的最大值为45
【知识点】判断数列的增减性、数列新定义、累加法求数列通项
【分析】(1)根据定义求出{b }即可;
n
(2)证明b −b >0即可得出;
n n+1
(3)首先证明a =1,a =2025的伴随数列是存在的,最小的m=2,然后确定m得到范围,求m得到最大
m
值,由(2)知a −a =m−1(n=1,2,...n−1),利用累加法可得a −1=(m−1)2,得出m−1≤ 2024,从而m≤45,
n+1 n m
2024
(m是整数)又由b −b = ∈N*知m−1是2024的正约数,这样得出m得到最大值为45,构造数列
1 m m−1
a =44n−43(n=1,2,...,44),a =2025,它存在伴随数列,从而得证.
n 45
4+10+16+19−4 4+10+16+19−10
【详解】(1)b = =15,b = =13,
1 4−1 2 4−1
4+10+16+19−16 4+10+16+19−19
b = =11,b = =10,均为正整数,
3 4−1 4 4−1
所以数列4,10,16,19存在“伴随数列”,且其“伴随数列”是15,13,11,10.
(2)因为数列{a }存在“伴随数列” {b },
n n
所以a −a >0(1≤n≤m−1),且b ,b ∈N*,
n+1 n n n+1
(a +a +...+a )−a (a +a +...+a )−a a −a
所以b −b = 1 2 m n − 1 2 m n+1 = n+1 n ∈N*,
n n+1 m−1 m−1 m−1
所以b −b >0,即b >b ,
n n+1 n n+1
所以b >b >b >...>b .
1 2 3 m
(3)①因为a =1,a =2025,其中m≥2,
1 m
(1+2025)−1 (1+2025)−2025
当m=2时,a =1,a =2025,有b = =2025 b = =1,均为正整数,
1 2 1 2−1 2 2−1
即当m=2时,数列1,2025存在“伴随数列”:2025,1,
因此m的最小值为2;
②一方面,由(2)知,a −a =(m−1)(b −b )≥m−1(n=1,2,...n−1),
n+1 n n n+1
于是a −1=(a −a )+(a −a )+...+(a −a )≥(m−1)+(m−1)+...+(m−1)=(m−1)2,
m m m−1 m−1 m−2 2 1
试卷第21页,共22页
学科网(北京)股份有限公司所以(m−1)2 ≤2024⇒m≤45 ( m∈N*) ,
另一方面,由数列{a }存在“伴随数列” {b },知
n n
(a +a +...+a )−a (a +a +...+a )−a a −a 2024
b −b = 1 2 m 1 − 1 2 m m = m 1 = ∈N*,
1 m m−1 m−1 m−1 m−1
所以m−1是2024的正约数,2024=2×2×2×11×23
m−1取2,4,8,11,22,23,44,46,88,92,184,253,506,1012,2024,
即m取3,5,9,12,23,24,45,47,89,93,185,254,507,1013,2025,
综合上述m=45为最大值,取a =44n−43(n=1,2,...,44),a =2025,
n 45
当1≤n≤44时,
(a +a +...+a )−a (1+45+89+...+1893+2025)−(44n−43)
b = 1 2 m n − =994−n∈N*,符合条件,
n 45−1 44
(a +a +...+a )−a (1+45+89+...+1893+2025)−2025
当n=45,b = 1 2 m n − =947∈N*,符合条件
n 45−1 44
因此m的最大值为45.
【点睛】关键点点睛:本题考查数列的新定义,解题关键是理解新定义, 新定义求解,在求m的最大值时,
注意数列与不等式的综合应用,解题时分两个方面,两方面确定满足题意的伴随数列存在,至少m=2是可
以的,另一方面,确定m得到最大值,利用累加法估计出m得到范围,再由伴随数列的性质得出m满足的
性质,由这两个确定出m得到最大值,但要构造出一个满足题意的数列,它的项数是m,且存在伴随数列.
试卷第22页,共22页