云南省三校联考（四）数学-答案(1)_2023年11月_0211月合集_2024届云南省三校高三高考备考实用性联考卷（四）_云南省三校2024届高三高考备考实用性联考卷（四）数学

2024 届云南三校高考备考实用性联考卷（四） 数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项符合题目要求） 题号 1 2 3 4 5 6 7 8 答案 D A B A A D B C 【解析】 1．由a 2a 3得a 32(a 3)，而a 34，故{a 3}是首项为4，公比为2的等 n1 n n1 n 1 n 比数列，所以a 32n1，即a 2n13，故选D． n n 2．先将其余三人全排列，共有A3种情况，再将 A 和 B 插空，共有A2种情况，所以共有 3 4 A2A3 12672种情况，故选A． 4 3 (2i)2 (34i)(1i) 1 7 1 7 3．由(1i)z(2i)2，可得z    i，所以z  i，故z在复 1i (1i)(1i) 2 2 2 2  1 7 平面内对应的点  ，  位于第二象限，故选B．  2 2 x3≥0， 4．题意可知 解得3≤x6，所以A{xN*|3≤x6}{3，4，5}，所以集合 A 6x0， 的真子集个数为23 17，故选A． x1 5．根据题意，构造函数 f(x)x1lnx，则 f(x) ，当x≥1时， f(x)≥0，所以 f(x) x 在区间 [1，) 上单调递增，因此可得 f(1.3) f(1)0 ，即 f(1.3)1.31ln1.3 0.3ln1.30，所以0.3ln1.3，又指数函数y2x为单调递增，可得20.3 2ln1.3，即bc．因 为a40.2 20.4 20.3 b，所以cba，故选A． π π 2π π   π 4  π  π 6．∵为锐角，   ，sin cos  ，cos2 2cos2   6 6 3 3   6 5  3  6 7 1 ，故选D． 25 数学参考答案·第1页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}      (t1)t120， 7．若a与b的夹角为钝角，则ab0且a与b不共线，所以 解得1t2 (t1)2t 0， 2   且t ，所以“1t2”是“a与b的夹角为钝角”的必要不充分条件，故选B． 3 8．由棱柱的定义可知①错；侧棱延伸后必须交于同一点，所以②错；由三角形两边之和大于 6 6 第三边，高相同，所以③对；外接球半径为R a，V  πa3，所以④对，故选C． 4 8 二、多项选择题（本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有 多项是符合题目要求的．全部选对的得5分，部分选对的得2分，有选错的得0分） 题号 9 10 11 12 答案 ABD AC ACD AC 【解析】 a b 9．对于A选项，由sinAsinB，根据正弦定理得  （r 为△ABC外接圆半径），即ab， 2r 2r 则AB，故A正确；对于B，由余弦定理知b2 a2 c2 2accosB，9a2 c2 ac，因 为a0，c0，所以9a2 c2 ac≥3ac ，ac≤3，当且仅当ac时等号成立，因为 1 3 3 3 S  acsinB ac，所以S 的最大值为 ，故B正确；对于C，由正弦定理 △ABC 2 4 △ABC 4 3 8 a b bsinA 2 2 3 得  ，则sinB   1，又ba，则B A60，知满足条 sinA sinB a 10 5 件的三角形只有一个，故 C 错误；对于 D， tanC tan[π(AB)]tan(AB) tanAtanB  ， 所 以 tanAtanBtanC(tanAtanB1) ， 所 以 tanAtanBtanC 1tanAtanB tanC(tanAtanB1)tanC tanAtanBtanC 0，所以tanA，tanB，tanC三个数有 0 个或2个为负数，又因A，B，C最多一个钝角，所以tanA0，tanB0，tanC 0，即 A，B，C都是锐角，所以△ABC一定为锐角三角形，故D正确，故选ABD． 3 3 3 3 4 4 2 10．由题意，P(B)  ，P(B )  ，P(B )   ，P(A|B) 1 334 10 2 334 10 3 334 10 5 1 80%， P(A|B )70%，P(A|B )75% ， 则 P(A)P(B)P(A|B)P(B )P(A|B ) 2 3 1 1 2 2 P(AB ) P(B )P(A|B )0.75，故A正确；由P(A)P(A|B ) 3 ，则P(AB )P(A)P(B )， 3 3 3 P(B ) 3 3 3 数学参考答案·第2页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}3 3 7 所以 A 与B 相互独立，故 B 错误；因为P(B ) ，所以P(B )1  ，所以 3 2 10 2 10 10 30.840.75 7  P(B A) P(A|B )P(B ) 34 10 P(B |A) 2  2 2  0.72，故C正确；由题意这次 2 P(A) P(A) 0.75 零件抽检中，1号、2号、3号车间生产零件合格数之比为8:7:10，所以从这次抽检的合 8 8 格零件中随机抽取一个，则该零件来自 1 号车间的概率为  ，该零件来自 2 8710 25 7 7 10 10 2 号车间的概率为  ，该零件来自3号车间的概率为   ，所以 8710 25 8710 25 5 该零件来自3号车间的概率最大，故D错误，故选AC． 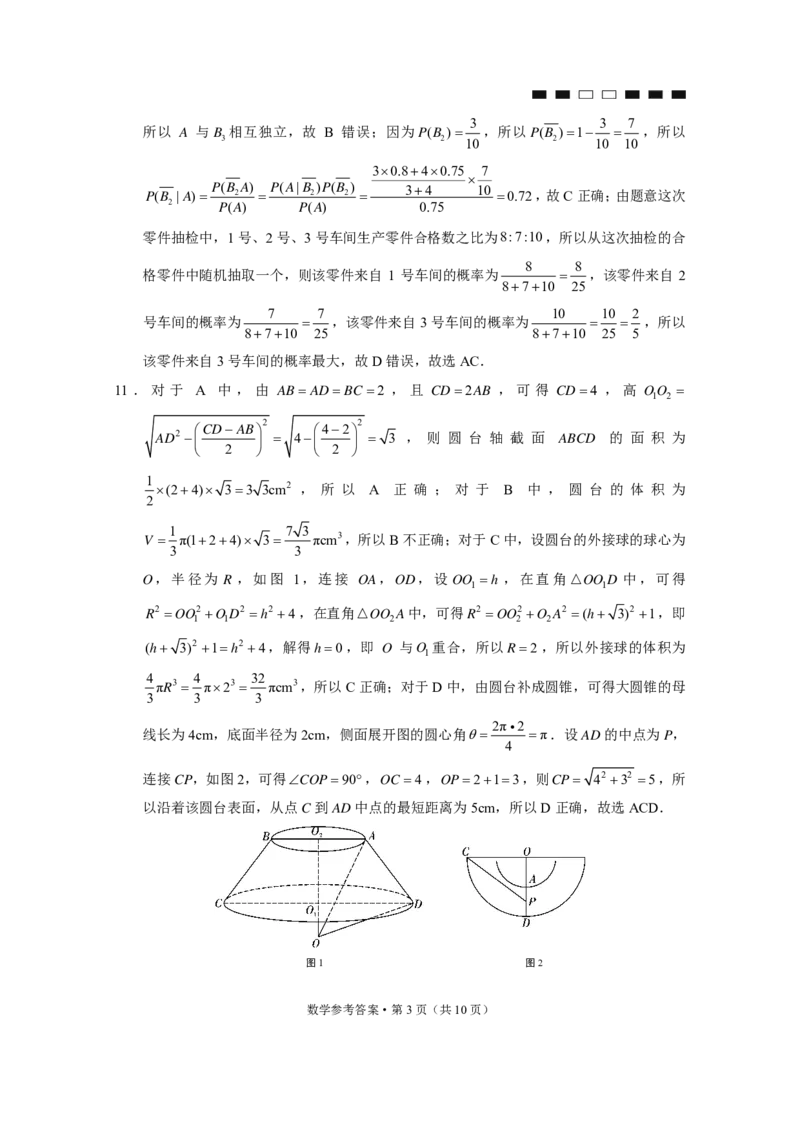11 ． 对 于 A 中 ， 由 AB ADBC 2 ， 且 CD2AB ， 可 得 CD4 ， 高 OO  1 2 2 2 CDAB 42 AD2    4   3 ， 则 圆 台 轴 截 面 ABCD 的 面 积 为  2   2  1 (24) 33 3cm2 ， 所 以 A 正 确 ； 对 于 B 中 ， 圆 台 的 体 积 为 2 1 7 3 V  π(124) 3 πcm3，所以B不正确；对于C中，设圆台的外接球的球心为 3 3 O，半径为 R ，如图 1，连接 OA，OD，设 OO h ，在直角△OOD 中，可得 1 1 R2 OO2 OD2 h2 4，在直角△OO A中，可得R2 OO2 O A2 (h 3)2 1，即 1 1 2 2 2 (h 3)2 1h2 4，解得h0，即 O 与O 重合，所以R2，所以外接球的体积为 1 4 4 32 πR3  π23  πcm3，所以C正确；对于D中，由圆台补成圆锥，可得大圆锥的母 3 3 3 2π2 线长为4cm，底面半径为2cm，侧面展开图的圆心角 π．设AD的中点为P， 4 连接CP，如图2，可得COP90，OC 4，OP213，则CP 42 32 5，所 以沿着该圆台表面，从点C到AD中点的最短距离为5cm，所以D正确，故选ACD． 图1 图2 数学参考答案·第3页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}12．对于 A，由 f(x)g(x)4 ，得 f(x2)g(x2)4 ，又 f(x)g(x2)4 ，所以 f(x2) f(x)，则 f(x)的图象关于直线x1对称，选项A正确；对于B，由于 f(x) 的图象关于点(0，2)对称，则 f(x) f(x)4，由选项A的结论可知，f(x2) f(x)， 则 f(x2) f(x)4，所以 f(x4) f(x2)4，则 f(x) f(x4)，所以函数 f(x)的 一个周期为 4，因为 f(x2) f(x)4，所以 f(1) f(3)4， f(2) f(4)4 ，所以 2004  f(k)501[f(4) f(1) f(2) f(3)]50184008 ，选项 B 错误；对于 C，由 k1 f(x) f(x4)，及 f(x)g(x)4，得g(x)g(x4)，则函数g(x)的一个周期为 4， π  4 选项C正确；对于D，取 f(x)sin x2，g(x) ，满足题设要求，但 2  π  sin x2 2  16 g(1)g(1) ，与g(x)的图象关于点(0，2)对称矛盾，则选项D错误，故选AC． 3 三、填空题（本大题共4小题，每小题5分，共20分） 题号 13 14 15 16  1 3   3 5 答案  ，  18   1，   15  10 10  5  【解析】     13．因为向量 a(5，2) ，b(1，3) ，所以向量 a 在向量b 上的投影向量的坐标为：      ab b 56 b 1  1 3  |a|        (1，3) ，  ． |a||b| |b| (1)2 32 (1)2 32 10  10 10 S n1 14．等差数列{a }的公差为d ，由等差数列前 n 项和公式可知 n a  d ；可得 n n 1 2 S S S  S S S  n1  n d为定值，所以 n 为等差数列，又 9  6 3，即 n 是以10为首项， n1 n  n  9 6  n  S 公差为1的等差数列，所以 9 10812，从而S 18． 9 9 b 2 5 15．根据题意，可得  ，即 5b2a ，平方的 5b2 4a2 ，又 a2 b2 c2 ，所以 a 5 c 3 5 5(c2 a2)4a2，即5c2 9a2，所以1  ． a 5 数学参考答案·第4页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}f(x ) f(2)(x ) f(n)(x ) 1 16．T (x) f(x ) 0 (xx ) 0 (xx )2  0 (xx )n，因为 f(x) ， n 0 1! 0 2! 0 n! 0 x f(1)1 ， 所 以 f(x)x2 f(2)(x)2x3 ， f(3)(x)6x4 ， f(4)(x)24x5 ， f(5)(x)120x6 ，又 f(1)1!， f(2)(1)2!， f(3)(1)63!， f(4)(1)244!， f(5)(1)1205!．所以T (x)1(x1)(x1)2 (x1)3(x1)4 (x1)5，故x3的系 5 数为C0 C1 C2 15． 3 4 5 四、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分10分） 5π π 解：（1）由题意可得A2，T 2  π，0，  6 3 2π 因为T  ，所以2．  π  π  π  因为A ，2 在 f(x)的图象上，所以 f  2sin2 2， 3  3  3  2π π π 所以 2kπ (kZ)，所以2kπ (kZ)． 3 2 6 π π  π 因为|| ，所以只有 满足要求，故 f(x)2sin2x  ． 2 6  6 …………………………………………………………………（5分）  π π π  π π （2）因为x  ， ，所以2x   ， ．      12 6 6  3 6 π π π  π  当2x  ，即x 时， f(x)取得最小值，最小值为 f   3． 6 3 12  12  π π 因为存在x  ， ，使得不等式 f(x)≤2a3成立，所以 f(x) ≤2a3，   12 6   min 3 3 即2a3≥- 3，解得a≥ ， 2  3 3  即a的取值范围为 ，． ……………………………………（10分）  2   18．（本小题满分12分） （1）证明：S na nn2，则S (n1)a n1(n1)2，n≥2， n n n1 n1 两式相减得a na (n1)a 12n1，n≥2， n n n1 数学参考答案·第5页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}因此(n1)a (n1)a 2(n1)，n≥2， n n1 所以a a 2，n≥2， n n1 故{a }是以a 1为首项，2为公差的等差数列． n 1 ∴a 12(n1)2n3，nN*． ………………………………………（6分） n （2）解：当n为奇数时，b a 2n3，当n为偶数时，b n2n． n n n ∴T (b b b )(b b b ) 20 1 3 19 2 4 20 (1335)(24442 643 20410) (135)10  (24442 643 20410) 2 170(24442 643 20410)， 设A 24442 643 20410，① 10 则4A 242 443 644 20411，② 10 ①−②，得3A 2(442 43 44 410)20411 10 24(1410)  20411 14 584118  3 584118 ∴A  ． 10 9 584118 故T 170 ，nN*． …………………………………（12分） 20 9 19．（本小题满分12分） 解：（1）设样本平均数的估计值为x， 则x 10(400.01500.02600.03700.024800.012900.004)． 解得：x 62．所以样本平均数的估计值为62． 前三组的频率和为0.10.20.30.6， 前四组的频率和为0.10.20.30.240.84， 第四组的频率为0.24， 0.70.6 25 415 所以70%分位数为65 1065  ． …………………（4分） 0.24 6 6 数学参考答案·第6页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}（2）因为学生的初试成绩X近似服从正态分布N(，2)，其中62，14． 所以26221490． 1 所以P(x≥90)P(x≥2) (10.9545)0.02275． 2 所以估计能参加复试的人数为0.022758000182人． ……………………………（8分） 1 1 （3）由该学生获一等奖的概率为 可知：a2b ． 8 8 3 1 3 则Pa2(1b)C1a(1a)ba2 2ab a2   ． 2 8 4a 8 1 3 令P f(a)a2   ，0a1． 4a 8 1 8a3 1 f(a)2a  ． 4a2 4a2 1 1 当0a 时， f(a)0；当 a1时， f(a)0． 2 2  1 1  所以 f(a)在区间 0，  上是减函数，在区间  ，1 上是增函数．  2 2  1 1 1 3 3 3 所以 f(a) min  f  2    4  2  8  8 ．所以P的最小值为 8 ． …………………………………………………………………（12分） 20．（本小题满分12分） （1）证明：∵BF⊥平面ACE，AE平面ACE，∴BF⊥AE， ∵二面角DABE为直二面角，且交线为AB，CB⊥AB，CB平面ABCD， ∴CB⊥平面ABE，AE平面ABE ∴CB⊥AE，BCBF B，BC，BF 平面BCE， ∴AE⊥平面BCE． ……………………………………………………………（4分） （2）解：以线段AB的中点为原点O，OE，AB所在直线分别为x轴，y轴，过点O平行 于AD的直线为z轴，建立如图3所示的空间直角坐标系， ∵AE⊥平面BCE，BE平面BCE，∴AE⊥BE， 在Rt△AEB中，AB4，O为AB的中点， ∴OE2，∴A(0，2，0)，E(2，0，0)，C(0，2，4)，   所以AE(2，2，0)，AC(0，4，4)，  设平面AEC的一个法向量为n(x，y，z)， 图3 数学参考答案·第7页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}  AEn0， 2x2y0， 则  即 ACn0， 4y4z0，  取x1，得n(1，1，1)，  又平面BAC的法向量为m(1，0，0)，     mn 1 3 ∴cos=     ， |m||n| 3 3 设二面角BACE的平面角为， 2  3 6 则sin 1   ，   3 3   6 ∴二面角BACE的正弦值为 ． ………………………………………（8分） 3 （3）解：∵AD∥z轴，AD4，  ∴AD(0，0，4)，   |ADn| 4 4 3 ∴点D到平面ACE的距离：d     ． ………………………（12分） |n| 3 3 21．（本小题满分12分） 1 解：（1）因为a1，所以 f(x) e2x 3ex 2x， 2 可得 f(x)e2x 3ex 2(ex 1)(ex 2)， 令 f(x)0ex(1，2)，即x(0，ln2)， 令 f(x)0x(，0)或x(ln2，)， 因此函数 f(x)的单调递减区间为(0，ln2)，单调递增区间为(，0)和(ln2，)． …………………………………………………………………（5分） （2）由题意可得 f(x)e2x 3aex 2a2 (ex a)(ex 2a)， 因为a0，所以令 f(x)0ex(a，2a)，即x(lna，ln2a)， 令 f(x)0x(，lna)或x(ln2a，)， 即函数 f(x)在(lna，ln2a)上单调递减，在(，lna)和(ln2a，)上单调递增，   5 f(lna)2lna a2 0，  5 e2    2 ae4， ，  2   f(ln2a)(2ln2a4)a2 0，   数学参考答案·第8页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}1 1 当x时， ex 3a f(x) e2x 3aex 2a2x0， 2 2 1 1 当x时， ex 3a f(x) e2x 3aex 2a2x0， 2 2 即函数 f(x)存在三个零点从小到大分布在区间(，lna)，(lna，ln2a)，(ln2a，)上，  5 e2  故实数a的取值范围为e4， ． ………………………………………（12分）  2    22．（本小题满分12分） 解：（1）依题意得c2，则F(2，0)，F (2，0)，而P(2， 2)， 1 2 于是2a|PF ||PF | 42 2 02 2 4 2， 1 2 从而a2 2 ．又a2 b2 c2，解得b2， x2 y2 所以椭圆C 的方程为  1． ………………………………………（4分） 1 8 4 （2）如图，设FA直线交椭圆于另一点B，F B直线交椭圆于另一点A， 1 2   由FAF B，故FA∥F B， 1 2 1 2 由椭圆对称性，|BF ||BF |，|AF ||AF |，且四边形ABAB为平行四边形． 2 1 1 2 （ⅰ）由题意，直线AB的斜率不为0，设直线AB：xty2， xty2， 由 消去x整理得(t2 2)y2 4ty40， x2 2y2 8， 4t 4 设A(x，y )，B(x，y )，则y  y  ，y y  ， 1 1 2 2 1 2 t2 2 1 2 t2 2     由FA3F BFA3FB y 3y （*），带入上式， 1 2 1 1 1 2 6t 2t 解得：y  ，y  ， 1 t2 2 2 t2 2 12t2 4   故  ，由于3，|FA||F B|，所以t0， (t2 2)2 t2 2 1 2 所以t 1，故FA的斜率为1． 1 xty2， （ⅱ）由 消去x整理得y2 ty20，由(t)2 80得t2 8． y2  x， 4 2(t2 1) 所以|AB| 1t2 | y  y | 1t2 (y  y )2 4y y  ， 1 2 1 2 1 2 t2 2 数学参考答案·第9页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}4 AB与BA间的距离d  （即点F 到AB的距离）， 2 t2 1 1 1 4 2(t2 1) 4 8 2 t2 1 故S  S     ， AF1F2B 2 ABAB 2 t2 2 t2 1 t2 2 1 令 t2 1s[1，3)，函数ys 在区间[1，3)上单调递增， s 1  10 所以ys   2，  ， s  3  8 2 t2 1 8 2s 8 2 12 2  则S     ，4 2， AF 1 F 2 B t2 2 s2 1 s 1   5  s 12 2  所以四边形AFF B的面积的取值范围为 ，4 2． ……………………（12分） 1 2  5   数学参考答案·第10页（共10页） {#{QQABBQAEogigAABAABgCQwXwCkMQkAGACCoORFAAsAIAgRNABCA=}#}