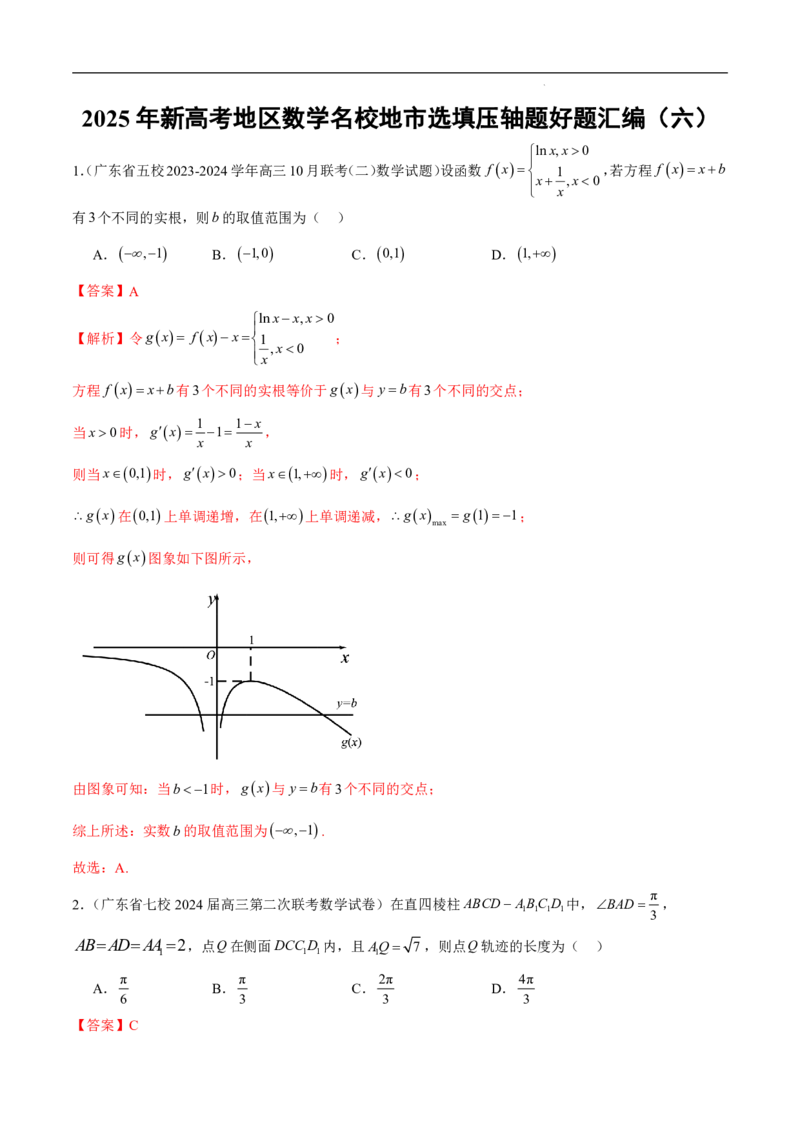2025年新高考地区数学名校地市选填压轴题好题汇编（六）（解析版）_2024-2025高三（6-6月题库）_2024年11月试卷_11272025年新高考地区数学名校地市选填压轴题好题汇编（六）

年新高考地区数学名校地市选填压轴题好题汇编（六） 2025 lnx,x0  1．（广东省五校2023-2024学年高三10月联考（二）数学试题）设函数 f x 1 ，若方程 f xxb x ,x0  x 有3个不同的实根，则b的取值范围为（ ） A．,1 B．1,0 C．0,1 D．1, 【答案】A lnxx,x0  【解析】令gx fxx1 ；  ,x0 x 方程 f xxb有3个不同的实根等价于gx与yb有3个不同的交点； 1 1x 当x0时，gx 1 ， x x 则当x0,1时，gx0；当x1,时，gx0； gx在0,1上单调递增，在1,上单调递减，gx  g11； max 则可得gx图象如下图所示， 由图象可知：当b1时，gx与yb有3个不同的交点； 综上所述：实数b的取值范围为,1 . 故选：A. 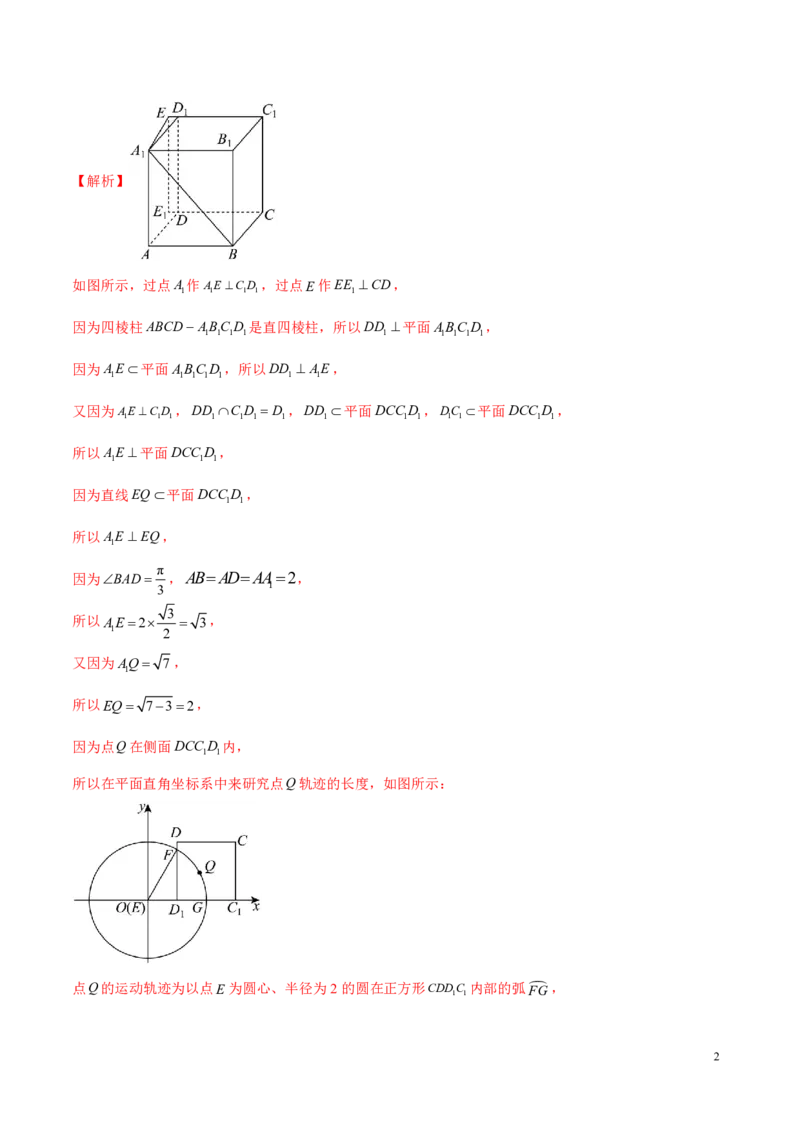π 2．（广东省七校2024届高三第二次联考数学试卷）在直四棱柱ABCD ABCD 中，BAD ， 1 1 1 1 3 ABADAA 2，点Q在侧面DCCD 内，且AQ 7，则点Q轨迹的长度为（ ） 1 1 1 1 π π 2π 4π A． B． C． D． 6 3 3 3 【答案】C 学科网（北京）股份有限公司【解析】 如图所示，过点A作AECD ，过点E作EE CD， 1 1 1 1 1 因为四棱柱ABCD ABCD 是直四棱柱，所以DD 平面ABCD ， 1 1 1 1 1 1 1 1 1 因为AE平面ABCD ，所以DD  AE， 1 1 1 1 1 1 1 又因为AECD ，DD CD D ，DD 平面DCCD ，DC 平面DCCD ， 1 1 1 1 1 1 1 1 1 1 1 1 1 1 所以AE 平面DCCD ， 1 1 1 因为直线EQ 平面DCCD ， 1 1 所以AE EQ， 1 π 因为BAD ，ABADAA 2， 3 1 3 所以AE2  3， 1 2 又因为AQ 7 ， 1 所以EQ 732， 因为点Q在侧面DCCD 内， 1 1 所以在平面直角坐标系中来研究点Q轨迹的长度，如图所示： 点Q的运动轨迹为以点E为圆心、半径为2的圆在正方形CDDC 内部的弧 FG ， 1 1 21 π 显然ED 2 1，OF 2，所以FOG ， 1 2 3 π 2π 所以FG 2 . 3 3 故选：C. 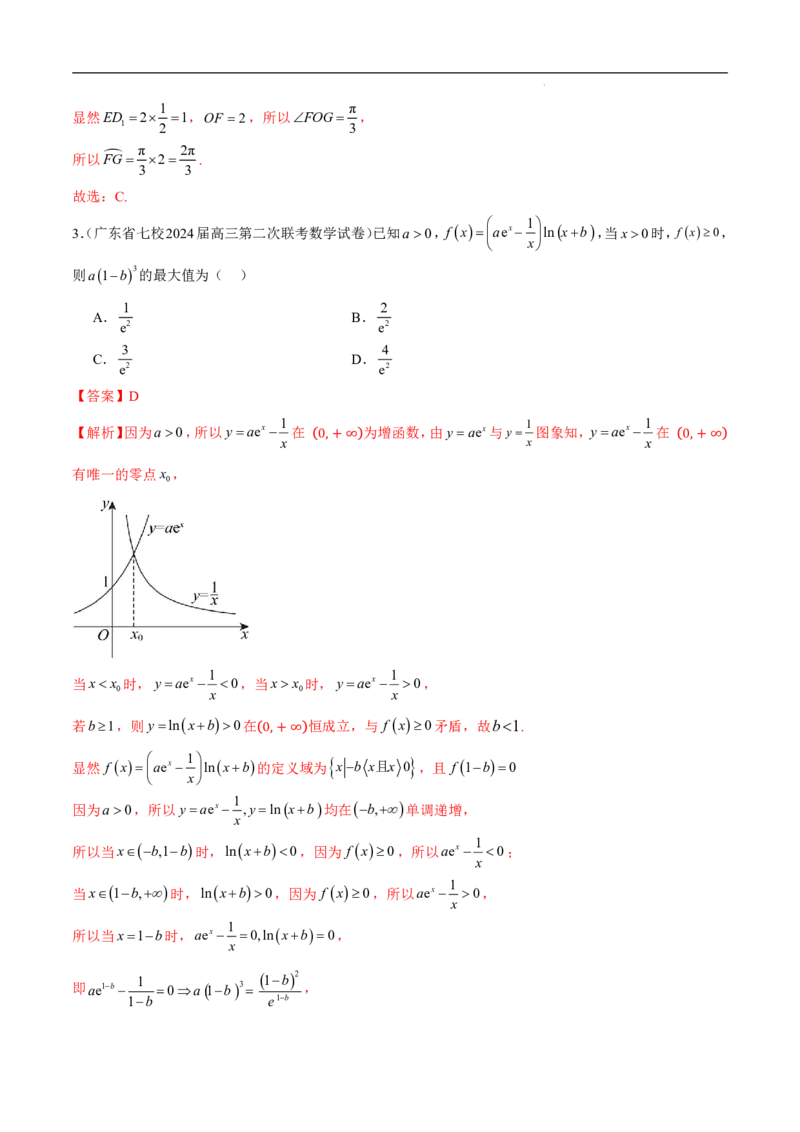 1 3．（广东省七校2024届高三第二次联考数学试卷）已知a0，f xaex lnxb，当x0时，f x0，  x 则a1b3的最大值为（ ） 1 2 A． B． e2 e2 3 4 C． D． e2 e2 【答案】D 1 1 1 【解析】因为a0，所以yaex 在 为增函数，由y aex与y 图象知，yaex 在 x x x 0,+∞ 0,+∞ 有唯一的零点x ， 0 1 1 当xx 时，yaex 0，当xx 时，yaex 0， 0 x 0 x 若b1，则ylnxb0在 恒成立，与 f x0矛盾，故b1. 显然 f x  aex  1 lnxb的 0, 定 + 义 ∞ 域为  x b x且x 0  ，且 f 1b0  x 1 因为a0，所以yaex ,ylnxb均在b,单调递增， x 1 所以当xb,1b时，lnxb0，因为 f x0，所以aex 0； x 1 当x1b,时，lnxb0，因为 f x0，所以aex  0， x 1 所以当x1b时，aex  0,lnxb0， x 1 1b2 即 ae1b 0a1b3 ， 1b e1b 学科网（北京）股份有限公司x2 2xx 令gx ，得gx ， ex ex 所以当x0,2时，gx0，gx x2 单调增， ex 当x2,时，gx0，gx x2 单调减， ex 4 故gx g2 ， e2 1b2 4 所以 a1b3  ，当且仅当1b2即b1时等号成立； e1b e2 故选：D x2 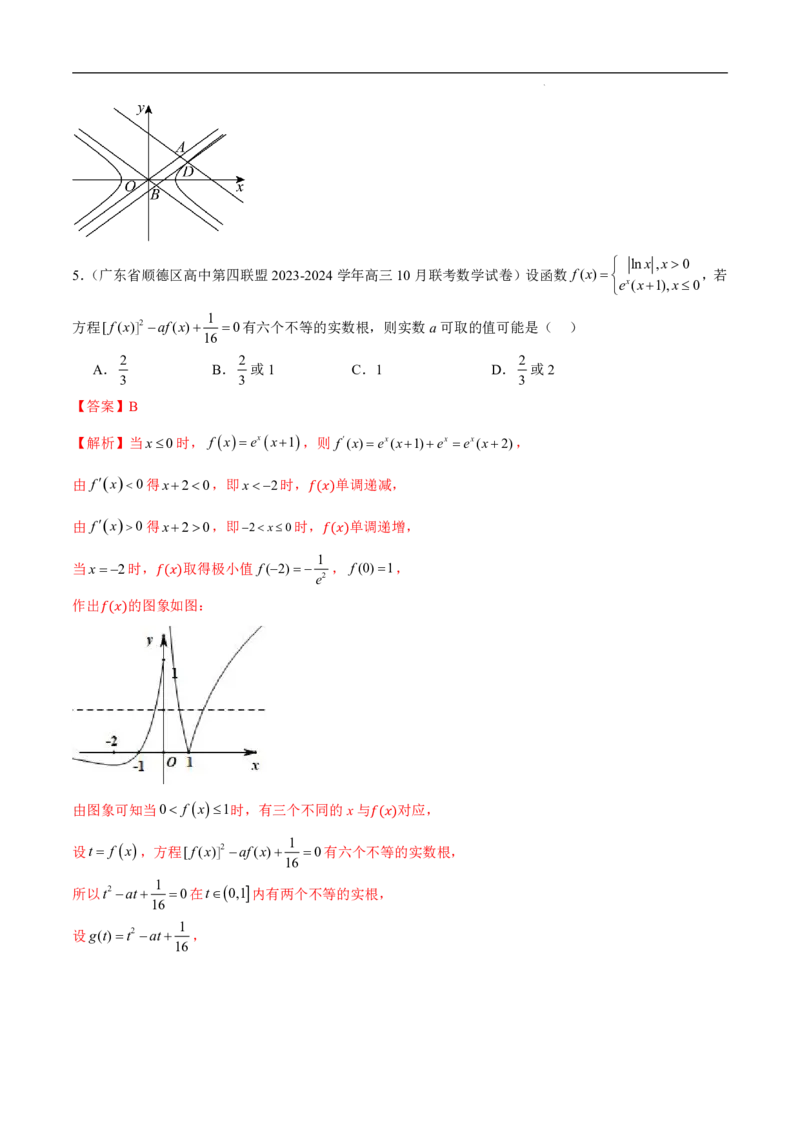4．（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知D为双曲线C:  y2 1右支上一点， 4 过点D分别作C的两条渐近线的平行线，与另外一条渐近线分别交于点A,B，则 DA DB （ ） 5 5 A．2 B． 5 C． D． 4 2 【答案】C 1 【解析】设坐标原点为O,Dx ,y ，易知C的渐近线的方程为y x， 0 0 2  1  1 y x, x x y   2   2 0 0 联立 解得 ，  yy  1 xx ,  y 1 x  1 y  0 2 0  4 0 2 0 1 1 1  1 1 1  不妨取A x y , x  y ，同理可得B x  y , x  y ， 2 0 0 4 0 2 0 2 0 0 4 0 2 0 2 2 1   1 1  5 1 5 1 则OA   x y   x  y   x y ,OB  x  y ， 2 0 0  4 0 2 0 2 2 0 0 2 2 0 0 因为四边形OADB是平行四边形， 5 1 5 1 5 1 于是 DA DB  OB OA  x  y  x  y  x2  y2 ， 2 2 0 0 2 2 0 0 4 4 0 0 x2 5 由于点D在C上，所以 0 y2 1，因此 DA DB  ，故C正确. 4 0 4 故选：C． 4 lnx ,x0 5．（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）设函数 f(x) ，若 ex(x1),x0 1 方程[f(x)]2af(x) 0有六个不等的实数根，则实数a可取的值可能是（ ） 16 2 2 2 A． B． 或1 C．1 D． 或2 3 3 3 【答案】B 【解析】当x0时， f xexx1，则 f(x)ex(x1)ex ex(x2)， 由 f ¢(x)<0得x20，即x2时， 单调递减， ( ) 由 f ¢(x)>0得x20，即2x0时， 单调递增， 1 ( ) 当x2时， 取得极小值 f(2) ， f(0)1， e2 作出 的图象 ( 如)图： ( ) 由图象可知当0 f x1时，有三个不同的x与 对应， 1 ( ) 设t f x，方程[f(x)]2af(x) 0有六个不等的实数根， 16 1 所以t2at 0在t0,1 内有两个不等的实根， 16 1 设g(t)t2at ， 16 学科网（北京）股份有限公司 1 0  16 g(0)0    1 g(1)0 1a 0   16 1 17 所以 0    a ，  a  a24 1 0 2 16  0 1  16  2  a  0 1  2 2 则实数a可能是 或1. 3 故选：B． x2 y2 6．（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）已知椭圆E：  1的左右 16 4 2  3 1 顶点分别为A，A ，圆O 的方程为x12y   ，动点P在曲线E上运动，动点Q在圆O 上运动， 1 2 1   1  2  4 若△AA P的面积为4 3，记 PQ 的最大值和最小值分别为m和n，则mn的值为（ ） 1 2 A． 7 B．2 7 C．3 7 D．4 7 【答案】B 【解析】椭圆E： x2  y2 1中，A(4,0),A (4,0)，设P(x ,y )，因△AAP的面积为4 3， 1 2 0 0 1 2 16 4 1 则 |AA || y |4| y |4 3，解得y  3或y  3，当y  3时，x 2，当y  3时，x 2， 2 1 2 0 0 0 0 0 0 0 0 即点P(2, 3)或P(2, 3)或P(2, 3)或P(2, 3)， 3 1 3 1 圆O :(x1)2 (y )2  圆心O(1, )，半径r ， 1 2 4 1 2 2 7 31 39 3 7 7 31 39 3 7 此时|PO | 或|PO | 或|PO | 或|PO | ，显然r    ， 1 2 1 2 1 2 1 2 2 2 2 2 3 7 又点Q在圆O 上运动，则有|PQ| |PO | r  r ， 1 max 1 max 2   7   此时点P 2, 3 ，|PQ| |PO | r  r ，此时P 2, 3 ， min 1 min 2 3 7 7 即m r,n r ，所以mn2 7 . 2 2 故选：B 7．（广东省肇庆市肇庆中学2024届高三10月月考数学试卷）已知函数 f xasin2xcos2x0图 π a  象的对称轴方程为xkπ ，kZ．则 f  π（ ） 4 4  62 2 A． B． C． 2 D． 2 2 2 【答案】C π 【解析】当a0时， f xcos2x，又函数对称轴为xkπ ，kZ ， 4 2π 1 则函数周期T  2π， ，函数 f xcosx，对称轴为xkπ，kZ，与题干不符； 2 2 1 当a0时， f xasin2xcos2x a2 1sin 2x，其中tan ， a π 2π 1 由函数 f x图象的对称轴方程为xkπ kZ，得 f x的最小正周期T  2π，所以 ， 4 2 2 所以 f xasinxcosx， π  π  由函数 f x图象的对称轴方程为xkπ kZ，得 f 2kπ x f xkZ， 4  2   π  π  π 令x0，得 f 2kπ  f 0kZ，即asin2kπ cos2kπ 1kZ，得a1，  2  2  2  π a  π π π 所以 f xsinxcosx 2sinx ，则 f  π f   2sin   2．  4 4  4 4 4 故选：C． 8．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）若x，y0，x y1，则 3x y的取值 范围为（ ） A．  1, 3  B．1,2 C．  3,2  D．   1 , 3   2  【答案】B 【解析】因为x y1，设x=cos2a,y=sin2a，  π 又由x，y0，不妨取 0, ，    2 π 所以 3x+ y = 3cos2a+ sin2a= 3cosa+sina=2sin a+ ， 3  π π π 5π 因为 0, ，所以a+ Î , ，    2 3 3 6 π 所以2sin a+ Î[1,2]， 3 所以 3x y的取值范围为1,2， 故选：B. 9．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）已知抛物线C：x2 4y的焦点为F ，过点F 学科网（北京）股份有限公司1 的直线与C相交于M ，N 两点，则2 MF  NF 的最小值为（ ） 2 9 7 A． B．4 C． D．3 2 2 【答案】A 【解析】 由抛物线C的方程为x2 4y，焦点坐标为 ， 0,1 设直线l的方程为：ykx1,Mx,y ,Nx ,y ， 1 1 2 2 x2 4y 联立方程 ，整理得x24kx40，则x x 4k,xx 4， ykx1 1 2 1 2 x2 x2 故y y  1  2 1， 1 2 4 4 p p 又 MF  y   y 1， NF  y   y 1， 1 2 1 2 2 2 1 1 1 5 1 5 9 则2 MF  NF 2y 1 y 12y  y  2 2y  y   ， 2 1 2 2 1 2 2 2 1 2 2 2 2 1 1 9 当且仅当y  ,y 2时等号成立，故2 MF  NF 的最小值为 . 1 2 2 2 2 故选：A. 10．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）从重量分别为1，2，3，4，…，10克的砝 码（每种砝码各2个）中选出若干个，使其总重量恰为9克的方法总数为m，下列各式的展开式中x9的系 数为m的选项是（ ） A．1x 1x2 1x3   1x10 B．1x12x13x  110x C．1x2 1x22 1x32 1x42   1x102 D．1x2 1xx22 1xx2x32   1xx2x102 【答案】C 8【解析】一个砝码有，9一种情况，C1 2种情况， 2 两个砝码有1,8，2,7，3，6，4,5几种情况C1C1416种 2 2 三个砝码有，1,1,7，1,2,6，1,3,5，1,4,4，2,2,5，2,3,4几种情况3C1 3C1C1C1 30种 2 2 2 2 四个砝码有，1,1,2,5，1,1,3,4，1,2,2,4，1,2,3,3，4C1C1 16种， 2 2 五个砝码有，1,1,2,2,3，C1 2种， 2 总计m66种. 对A，选项x9系数为8，故不符合，所以A错误； 对B，x9的系数是选9个带x的，其他的1个括号选常数项，可得C9 1066，故B错误； 10 对C，1x2 1x22 1x32 1x42   1x102 1x 1x2 1x3 1x4   1x101x 1x2 1x3 1x4   1x10 x9系数为x9单独组成，其他为常数，则有C1 2种，系数为2 2 x9有两项组成，系数为x与x8组成，其他为常数，C1C1 4，系数为4， 2 2 x9系数为x2与x7组成，其他为常数，C1C1 4，系数为4， 2 2 x9系数为x3与x6组成，其他为常数， C1C1 4，系数为4， 2 2 x9系数为x4与x5组成，其他为常数， C1C1 4，系数为4， 2 2 同理x9由三项组成x,x,x7，x,x2,x6，x,x3,x5，x,x4,x4，x2,x2,x5，x2,x3,x4几种情况，其他项为常数，则 系数为3C1 3C1C1C1 30 2 2 2 2 同理x9由四项组成x,x,x2,x5，x,x,x3,x4，x,x2,x2,x4，x,x2,x3,x3几种情况，其他为常数，则系数4C1C1 16， 2 2 同理x9由五项组成x,x,x2,x2,x3其他项为常数，则系数为C1 2， 2 综上x9系数为m66，故C正确； 对D， 1x2 1xx22 1xx2x32   1xx2x102 1x 1xx2 1xx2x3   1xx2x10  学科网（北京）股份有限公司1x 1xx2 1xx2x3   1xx2x10 ， x5系数直接有x5一项，其他是常数项，可有2C1 12种情况，系数为12， 6 x5有x与x4组成，其他是常数项，可有2C1C1 10860, 9 6 故D错误. 故选：C 11．（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）在平面直角坐标系xOy中，已知直线 1 l:ykx 与圆C:x2 y2 1交于A,B两点，则VAOB的面积的最大值为（ ） 2 1 3 3 A．1 B． C． D． 2 2 4 【答案】D 1  1 【解析】根据题意可得直线l:ykx 恒过点E0, ，该点在已知圆内， 2  2 圆C:x2 y2 1的圆心为C0,0，半径r 1，作CDl于点D，如下图所示： 1 CD 1 易知圆心C到直线l的距离为 CD  CE  ，所以cosDCB  ， 2 CB 2  π π π 又DCB0, ，可得DCB  , ；  2 3 2 2π  因此可得ACB2DCB  ,π，  3  1 1 2π 3 所以VAOB的面积为S  CA CB sinACB 11sin  . AOB 2 2 3 4 故选：D 12．（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）设函数 f x  x2axb  lnx，若 f x0， 则a的最小值为（ ） A．2 B．1 C．2 D．1 【答案】B 10【解析】函数 f(x)定义域为(0,)，而0 x1lnx0，x1lnx0，x1lnx0， 要使 f x0，则二次函数yx2axb，在0x1上y0，在x1上y0， 所以x1为该二次函数的一个零点，易得ba1， 则y x2ax(a1)(x1)[x(a1)]，且开口向上， 所以，只需(a1)0a10a1，故a的最小值为1. 故选：B 13．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）在平面直角坐标系中，双曲线 x2 y2 C:  1  a0,b0 的左､右焦点分别为F,F ,A为双曲线右支上一点，连接AF 交y轴于点B，若 a2 b2 1 2 1 AB  AF ，且AF  AF ，则双曲线的离心率为（ ） 2 1 2 A． 1 2 B． 2 2 C． 5 D． 6 【答案】B 【解析】设 AB  AF m0，则 AF 2am， BF 2a， 2 1 1 AF OF 因为BOFF ,AF  AF ，则cosAFF  1  1 ， 1 2 1 2 1 2 FF BF 1 2 1 2am c c2 c2 即  ，整理可得m 2a，则 AF  ， 2c 2a a 1 a c2  2 c2  2 又因为 AF 2 AF 2  FF 2，即    2a 2c2， 1 2 1 2  a   a  整理可得e44e220，解得e2 2 2或e2 2 2（舍去）， 所以双曲线的离心率为 e 2 2 . 故选：B. 14．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）已知函数 f xcosxax在 学科网（北京）股份有限公司 π 区间 0, 单调递增，则实数a的取值范围是（ ）    6  1  3 1   3  A．,  B．  ,  C．  , D． ,   2  2  2   2  【答案】A 【解析】因为 f xcosxax，则 fxsinxa，  π 由题意可得 fxsinxa0对任意x 0, 恒成立，    6  π 即sinxa对任意x  0,  恒成立，  6  π  1  1 又因为x  0,  ，则sinx   ,0  ，可得a ，  6  2  2  1 所以实数a的取值范围是, .  2 故选：A.  1 15．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）已知函数 f xlnxax   x 有两个极值点x ,x ，则 f x x 的取值范围是（ ） 1 2 1 2  3  3   3  3  A．0,ln2  B．ln2 , C．0,2ln2  D．ln2 ,  4  2   2  4  【答案】D 1  1  ax2xa 【解析】由题意可知： f x的定义域为0,，且 fx a1  ， x  x2  x 由题意可知：ax2 xa0有两个不相等的正根x ,x ， 1 2 1 显然a0，即x2 x10有两个不相等的正根x ,x ， a 1 2  1 Δ 40  a2   1 1 则x x   0，解得0a ，  1 2 a 2 x x 10 1 2   1 1 1  可得 f x x  f   ln a aa 2lna1 ， 1 2 a a a  1 1 2a21 令gaa2lna1,0a ，则ga2a  0， 2 a a  1 1 3 可知ga在0, 内单调递减，则gag  ln2 ，  2 2 4 12且当a趋近于0时，ga趋近于，  3   3  即ga的值域为ln2 ,，所以 f x x 的取值范围是ln2 ,.  4  1 2  4  故选：D. 16．（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）已知aR，设函数 x22ax2a, x1, f(x) 若关于x的不等式 f(x)0在R上恒成立，则a的取值范围为 xalnx, x1, A．0,1 B． 0,2  C．  0,e  D．1,e 【答案】C 【解析】先判断a0时，x22ax2a0在(,1]上恒成立；若xalnx0在(1,)上恒成立，转化为 x a 在(1,)上恒成立．∵ f(0)0，即a0， lnx （1）当0a1时， f(x) x22ax2a(xa)22aa2 2aa2 a(2a)0， 当a1时， f(1)10， 故当a0时，x22ax2a0在(,1]上恒成立； x 若xalnx0在(1,)上恒成立，即a 在(1,)上恒成立， lnx x lnx1 令g(x) ，则g'(x) ， lnx (lnx)2 当xe,函数单增，当0 xe,函数单减， 故gx gee，所以ae．当a0时，x22ax2a0在(,1]上恒成立； min 综上可知，a的取值范围是[0,e]， 故选C． 17．（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）已知函数 f x f x,xR， f 5.51，函数gxx1 f x，若gx1为偶函数，则g0.5的值为（ ） A．3 B．2.5 C．2 D．1.5 【答案】D 【解析】因为函数gx1为偶函数，可gx的图象关于x1对称，所以gx g2x， 由gxx1 f x，可得x1 f x1x f 2x， 学科网（北京）股份有限公司即 f x f 2x0，所以函数 f x关于(1,0)对称， 又因为 f x f x，所以 f x是定义在R上的偶函数， 所以 f xf 2xf(x2)， 所以 f x4 f[(x2)2]f(x2)[f(x)] f(x)，即 f(x4) f(x)， 所以函数 f x是周期为4的周期函数， 所以 f(5.5) f(1.54) f(1.5) f(2.5) f(2.5)1， 则g(0.5)g(2.5)(2.51)f(2.5)1.5. 故选：D. 18．（湖北省新八校协作体2023-2024学年高三10月联考数学试题）已知函数 f x的定义域为R， y f x2ex是偶函数，y f x4ex是奇函数，则 f x的最小值为（ ） A．e B．2 2 C．2 3 D．2e 【答案】C 【解析】因为y f x2ex是偶函数，所以 f x2ex  f x2ex，即 f(x) f(x)2ex2ex①， 又因为y f x4ex是奇函数，所以 f(x)4ex f(x)4ex，即 f(x) f(x)4ex4ex②， 联立①②可得 f(x)ex3ex， 1 由基本不等式得 f(x)ex3ex 2 3，当且仅当ex 3ex，即x ln3时等号成立， 2 所以 f x的最小值为2 3， 故选：C． lnx  ,x0 19．（湖北省新八校协作体2023-2024学年高三10月联考数学试题）已知函数 f x   x ，若函数  ex  ,x0  x xk gx f x 恰有2个零点，则实数k的取值范围是（ ） x A．1,e B．，1 e， C．[1,1) D．，11， 【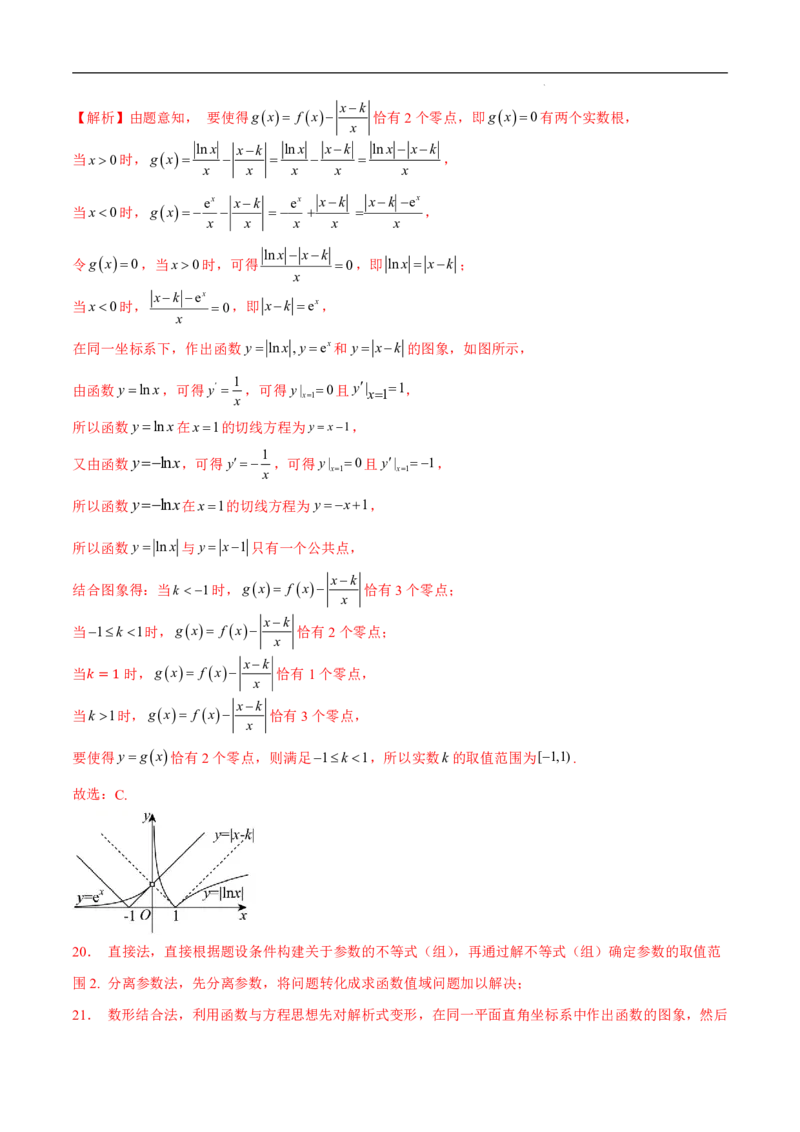答案】C 14xk 【解析】由题意知， 要使得gx f x 恰有2个零点，即gx0有两个实数根， x lnx xk lnx xk lnx  xk 当x0时，gx     ， x x x x x ex xk ex xk xk ex 当x0时，gx     ， x x x x x lnx  xk 令gx0，当x0时，可得 0，即 lnx  xk ； x xk ex 当x0时， 0，即 xk ex， x 在同一坐标系下，作出函数y lnx,yex和y xk 的图象，如图所示， 1 由函数ylnx，可得y  x ，可得y| x1 0且y| x1 1， 所以函数ylnx在x1的切线方程为yx1， 1 又由函数ylnx，可得y ，可得y| 0且y| 1， x x1 x1 所以函数ylnx在x1的切线方程为yx1， 所以函数y lnx 与y x1只有一个公共点， xk 结合图象得：当k 1时，gx f x 恰有3个零点； x xk 当1k 1时，gx f x 恰有2个零点； x xk 当 时，gx f x 恰有1个零点， x =1 xk 当k 1时，gx f x 恰有3个零点， x 要使得ygx恰有2个零点，则满足1k 1，所以实数k的取值范围为[1,1). 故选：C. 20． 直接法，直接根据题设条件构建关于参数的不等式（组），再通过解不等式（组）确定参数的取值范 围2. 分离参数法，先分离参数，将问题转化成求函数值域问题加以解决； 21． 数形结合法，利用函数与方程思想先对解析式变形，在同一平面直角坐标系中作出函数的图象，然后 学科网（北京）股份有限公司数形结合求解. 结论拓展：与ex和lnx相关的常见同构模型 ①aea blnbealnea blnb，构造函数 f xxlnx或gxxex； ea b ea b x ex ②    ，构造函数 f x 或gx ； a lnb lnea lnb lnx x ③ea ablnbea lnea blnb，构造函数 f xxlnx或gxexx. 22．（河南省七校联考2024届高三第二次联合教学质量检测数学试题）如图所示，直线ykxm与曲线 相切于  x, f x  ,  x , f x  两点，其中x x ．若当x0,x 时，fxk，则函数 f xkx在 = 1 1 2 2 1 2 1 上的极大值点个数为（ ） 0,+ ∞ A．0 B．1 C．2 D．3 【答案】D 【解析】 根据图象，可分别作出 f x斜率为k的另外三条切线：ykxm i1,2,3，切点分别为x ,x ,x ， i 5 3 4 如图所示：当x0,x x ,x x ,x 时， fxk；当xx,x x ,x x ,时， fxk； 1 3 2 4 5 1 3 2 4 5 设gx f xkx，则gx fxk， gx在0,x ,x ,x ,x ,x 上单调递增，在x,x ,x ,x ,x ,上单调递减， 1 3 2 4 5 1 3 2 4 5 gx f xkx有x x ，xx 和xx 三个极大值点. 1 2 5 故选：D.  π 23．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）将函数 f(x)cosx (06)  6 π 的图象向右平移 个单位长度得到函数g(x)的图象，若g(x)是奇函数，则 f(x)在区间(0,π)内的极值点个 6 数为（ ） 16A．1 B．2 C．3 D．4 【答案】D 【解析】若g(x)是奇函数，则g(x)图象关于(0,0)对称， π 由题意得g(x)的图象向左移 个单位长度得到函数 f(x)的图象， 6  π    故 f(x)的图象关于 ,0对称， f(x)cosx ，  6   6       则cos  0，则   k,kZ，  6 6 6 6 2 解得6k2,kZ，又因为06， 则当k 1时，ω=4.   f(x)cos4x ，x(0,π)，  6 π π 25π 令t 4x  , ， 6 6 6  π 25π 则htcost在 , 极值点的个数与 f(x)在区间(0,π)内的极值点个数相同. 6 6  π 25π 而函数htcost在 , 内的所有极值点为π,2π,3π,4π，共4个. 6 6  故 f(x)在区间(0,π)内的极值点个数也为4个. 故选：D. 24．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知函数 f x的定义域为R, f x1 为奇函数， f x2为偶函数，则 f 1 f 2L f 16（ ） A．0 B．16 C．22 D．32 【答案】B 【解析】因为 f x1为奇函数，则 f 01，且函数 f(x)的图象关于 中心对称，即 f x f x2， 0,1 因为 f x2为偶函数，所以 f x2 f 2x，则 f x4 f x， 所以 f x f x42， f x4 f x82，所以 f x f x8，故 f x的周期为8， 因为 f 1 f 52, f 2 f 62, f 3 f 72, f 4 f 82， 所以 f 1 f 2 f 162 f 1 f 2 f 8  16， 故选：B. 25．（河南省部分名校2023-2024学年高三10月月考数学试卷）已知函数 f x及其导函数 的定义域均 ' 学科网（北京）股份有限公司20 为 ，若 f x f x2x, f x的图象关于直线x1对称，且 f 20，则 f(20)f(i)（ ） i1 A．10 B．20 C．10 D．20 【答案】A 【解析】 f(x)的图象关于直线x1对称，则 f(x) f(2x)， 所以 f(x)f(2x)，又 f(x) f(x)2x，则 f(x)f(x)2， 所以f(2x)f(x)2，从而 f(2x) f(x)2， 因此{f(2n)}及{f(2n1)}是公差为2的等差数列，其中nN， 又在 f(x)f(2x)中令x1得 f(1)f(1)，即得 f(1)0， 在 f(x)f(x)2中令x0得 f(0)f(0)2，则 f(0)1，因此 f(2)1， 于是 f(1) f(3) f(5) f(19)0241890， f(2) f(4) f(20)1319100， 20 所以 f(i)190， i1 又由 f(x) f(2x)及 f x f x2x得 f(2x) f(x)2x， 从而 f(2x) f(x)2x，而 f(2)0 所以 f(20) f(18)36 f(16)3236 f(2)483236 180， 20 所以 f(20) f(i)180(190)10， i1 故选：A． 26．（河南省部分名校2024届高三月考（一）数学试题）VABC与△ABD都是边长为2的正三角形，沿公 共边AB折叠成三棱锥且CD长为 3 ，若点A，B，C，D在同一球O的球面上，则球O的表面积为（ ） 13 208π 112π 52 A． π B． C． D． π 9 9 3 9 【答案】D 【解析】设AB的中点为E，正VABC与正△ABD的中心分别为N ，M ，如图， 18根据正三角形的性质有M ，N 分别在DE，CE上，OM 平面ABD，ON 平面ABC， 因为VABC与△ABD都是边长为2的正三角形，则DE CE  3，又CD 3， 则CDE是正三角形， 又ABDE，AB^CE，CEDE E ，CE,DE平面CDE， 所以AB平面CDE，所以O在平面CDE内， 1 3 故EM EN  ED ，易得RtMEO≌RtNEO， 3 3 故MEONEO30， 2 ME 2 2 13 故OE  ，又EB=1，故球O的半径OB 12   ， cos30 3 3 3 2  13 52π 故球O的表面积为S 4π   ．    3  9 故选：D． 27．（河南省部分名校2024届高三月考（一）数学试题）已知函数 f x及其导函数 fx在定义域均为R且 Fxex2f x2是偶函数，其函数图象为不间断曲线且x2 fx f x  0，则不等式 xf lnxe3f 3的解集为（ ） A．  0,e3 B．  1,e3 C．  e,e3 D．  e3,  【答案】C 【解析】由x2 fx f x  0,得x fx2 f x2  0, 则当 时,得 fx2 f x20, >0 Fxex2f x2ex2fx2ex2 f x2 fx2  ， 学科网（北京）股份有限公司则当 时,Fx0,得函数Fx在0,上单调递增, >0 因为xf lnxe3f 3 ,所以Flnx2F1 , 由于Fxex2f x2是偶函数,则F  lnx2 F1 , 而函数Fx在0,上单调递增,得 lnx2 1, 得1lnx21, 得e xe3, 故选：C. 28．（多选题）（广东省五校2023-2024学年高三10月联考（二）数学试题）若x，y满足x2  y2 xy1， 则（ ） A．xy1 B．xy2 C．x2 y2 2 D．x2 y2 1 【答案】BC ab 2 a2b2 xy 2 【解析】因为ab   （a,bÎR），由x2  y2 xy1可变形为，xy213xy3  ，  2  2  2  解得2 x y 2，当且仅当x y1时，x y2，当且仅当x y1时，x y2，所以A错误，B 正确； 由x2  y2 xy1可变形为 x2y2 1xy x2y2 ，解得x2 y2 2，当且仅当x y1时取等号，所以 2 C正确； 2  y 3 y 3 因为x2  y2 xy1变形可得 x   y21，设x cos, ysin，所以  2 4 2 2 1 2 5 2 1 1 1 xcos sin,y sin，因此x2y2 cos2 sin2 sincos1 sin2 cos2 3 3 3 3 3 3 3 4 2  π 2  3 3   sin2   ,2  ，所以当x ,y 时满足等式，但是x2 y2 1不成立，所以D错误． 3 3  6 3  3 3 故选：BC． 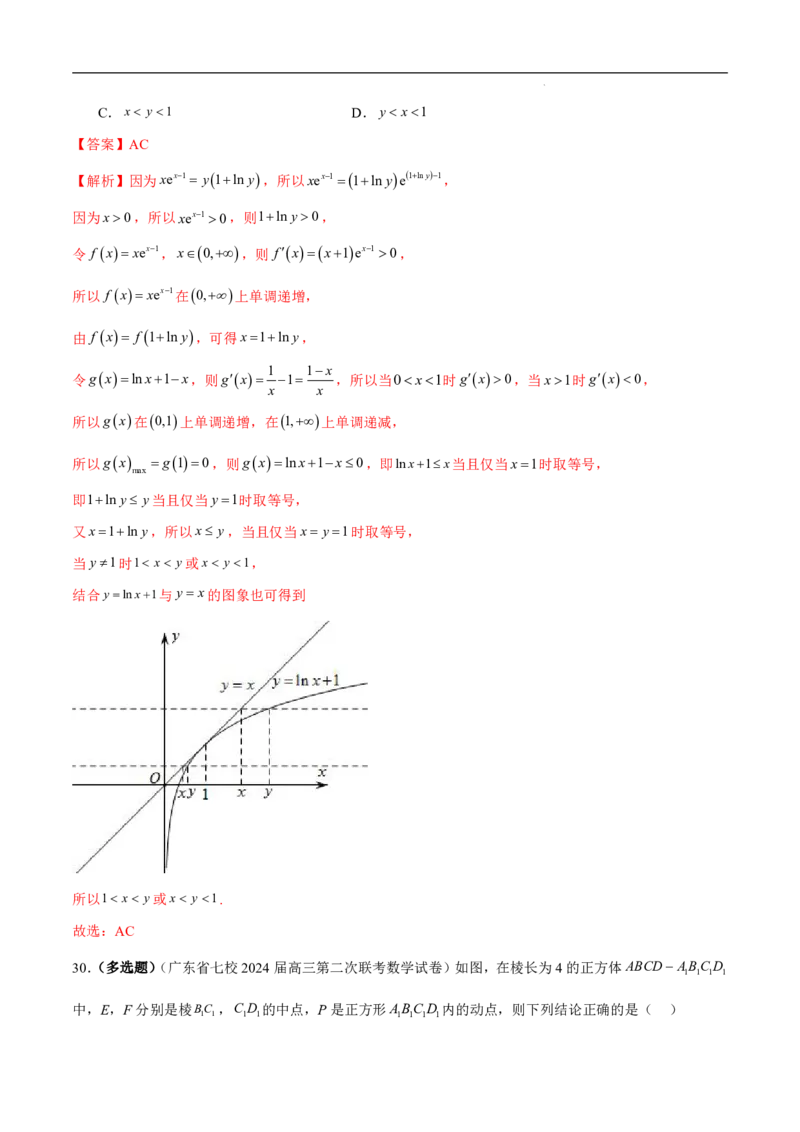29．（多选题）（广东省五校2023-2024学年高三10月联考（二）数学试题）若正实数x，y满足xex1  y1lny， 则下列不等式中可能成立的是（ ） A．1 x y B．1 yx 20C．x y 1 D．y x1 【答案】AC 【解析】因为xex1  y1lny，所以xex11lnye 1lny1， 因为x0，所以xex10，则1lny0， 令 f x xex1，x0,，则 fxx1ex10， 所以 f x xex1在0,上单调递增， 由 f x f 1lny，可得x1lny， 1 1x 令gxlnx1x，则gx 1 ，所以当0x1时gx0，当x1时gx0， x x 所以gx在0,1上单调递增，在1,上单调递减， 所以gx g10，则gxlnx1x0，即lnx1x当且仅当x1时取等号， max 即1lny y当且仅当y1时取等号， 又x1lny，所以x y，当且仅当x y1时取等号， 当y1时1 x y或x y 1， 结合ylnx1与y x的图象也可得到 所以1 x y或x y 1. 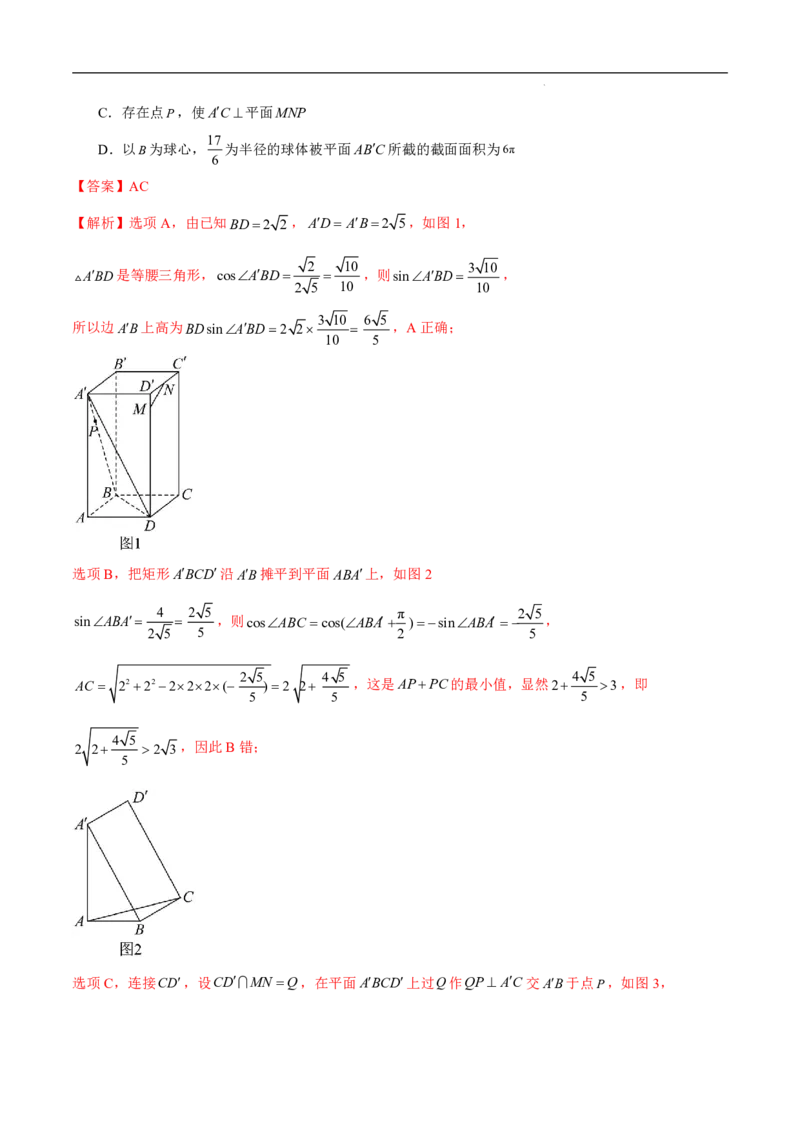故选：AC 30．（多选题）（广东省七校2024届高三第二次联考数学试卷）如图，在棱长为4的正方体ABCD ABCD 1 1 1 1 中，E，F分别是棱BC ，C D 的中点，P是正方形ABCD 内的动点，则下列结论正确的是（ ） 1 1 1 1 1 1 1 1 学科网（北京）股份有限公司A．若DP//平面CEF，则点P的轨迹长度为2 2 B．若DP//平面CEF，则三棱锥PDEF的体积为定值 C．若AP 17，则点P的轨迹长度为2 D．若P是棱AB 的中点，则三棱锥PCEF 的外接球的表面积是 1 1 【答案】ABD 【解析】对A选项，如图， 分别取AD ，AB 的中点N，M， 1 1 1 1 则易得MN//EF，MN//DB，DN//CE， MNDN N，EFCEE， MN,DN 平面MNDB，EF,CE平面CEF 从而易得平面MNDB//平面CEF， 又P是正方形ABCD 内的动点，且DP//平面CEF， 1 1 1 1 ∴P点的轨迹为线段NM，又MN 2 2，∴A选项正确； 对B选项，由A选项分析可知P点的轨迹为线段NM，MN//EF， ∴三角形PEF的面积为定值，又D到平面PEF的距离也为定值， ∴三棱锥PDEF的体积为定值，∴B选项正确； 对C选项，如图，若AP 17，又AA 4，且AA 平面ABCD ， 1 1 1 1 1 1 22则AP AP2 AA2  17 16 1， 1 1 ∴P点的轨迹是正方形ABCD 内以A为圆心，1为半径的四分之一圆弧， 1 1 1 1 1 1  ∴P的轨迹长度为 21 ，∴C选项错误； 4 2 对D选项，如图， 若P是棱AB 的中点，取PF 的中点G，AC的中点H， 1 1 则FEPE，∴G到E，F，P的距离相等，又GH 平面PEF， ∴三棱锥PCEF 的外接球的球心O在GH 上， 设GOt，则OH 4t，又PG2，HC2 2， 设三棱锥PCEF 的外接球的半径为R，则POCOR， ∴在RtPGO与RtHCO中，根据勾股定理可得： R2 22t2   2 2 2 4t2，解得t  5 ， 2 25 41 ∴R2 4t2 4  ， 4 4 ∴三棱锥PCEF 的外接球的表面积是4R2 41，∴D选项正确. 故选：ABD. 31．（多选题）（广东省七校2024届高三第二次联考数学试卷）已知抛物线C:x2 4y的焦点为F，A，B，P   为抛物线C上的点，cosFA,FB1，若抛物线C在点A，B处的切线的斜率分别为k ,k ，且两切线交于 1 2 点M．N为抛物线C的准线与y轴的交点．则以下结论正确的是（ ） 学科网（北京）股份有限公司  π A．若 AF  BF 4，则 AFBF 1 B．直线PN的倾斜角 4 C．若k k 2，则直线AB的方程为xy10 D．|MF |的最小值为2 1 2 【答案】BCD     【解析】由题cosFA,FB1，则向量FA,FB的夹角为π，故F，A，B三点共线， 设AB:ykx1，与C的方程联立得x24kx40，设Ax,y ,Bx ,y ， 1 1 2 2 则x x 4k，xx 4，故y  y 4k2 2, y y 1， 1 2 1 2 1 2 1 2 由抛物线的定义得|AF| y 1,|BF| y 1， 1 2  故 AF  BF  y y 24k244，k 0， FA·FB4 ，所以A错误； 1 2  x2  π 设Px , 0 ，N(0,1)，当x 0时，直线PN倾斜角大于等于 ，  0 4  0 2 x2 0 1 π 当x 0 0时， k PN  4 x  x 4 0  x 1 2 x 4 0  x 1 1 ，所以直线PN的倾斜角 4 ，B正确； 0 0 0 记直线AB的斜率为k，令 f(x) 1 x2，则 f(x) 1 x，则k  fx  1 x,k  fx  1 x ， 4 2 1 1 2 1 2 2 2 2 x2x2 2 1 又 k  y 2 y 1  4  1 x x  ，所以k 1 k 2 2k，所以k 1，又直线AB过点F(0,1)，故直线AB的方 x x x x 4 2 1 2 1 2 1 程为xy10,C正确； x x2 x x2 MA:yy  1xx ，又y  1 ，所以MA:y 1 x 1 ， 1 2 1 1 4 2 4 x x2 x x xx  同理MB:y 2 x 2 ，联立解得M 1 2 , 1 2 ，即M(2k,1)，又F(0,1)， 2 4  2 4  所以|MF| 4k242，当k 0时，等号成立，所以 MF 的最小值为2，D正确； 故选:BCD. 2432．（多选题）（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知函数 f x不是常函数， 且图象是一条连续不断的曲线，记 f x的导函数为 fx，则（ ） A．存在 f x和实数t，使得 fxtf x B．不存在 f x和实数t，满足 f x f t f 2x C．存在 f x和实数t，满足 f  xt tf x D．若存在实数t满足 fx f xt，则 f x只能是指数函数 【答案】AC 【解析】令 f xax，则存在实数lna使得 fxaxlna，A正确； 存在t2, f xlog x, f x f tlog xlog 2log 2x f 2x，故B错误； a a a a 令 f xlog x，则 f  xt log xt tlog xtf x，C正确； a a a  π 若 f xsinx， fxcosxsinx ，故D错误．  2 故选：AC． 33．（多选题）（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知F1,0，圆M :(x1)2 y2 1， 点P为圆M 上一动点，以PF 为直径的圆N 交y轴于A,B两点，设Ax ,y ,Bx ,y ,Px ,y ，则（ ） A A B B P P 1 3 A．当点N 在y轴上时， PF  5 B． MN 的取值范围是  ,  2 2 1 C．y y  x D．cosAFP A B P BF 【答案】ACD 【解析】 当N 在y轴上时， x x 1，则 x x 2x 1,y 1，则 PF  5，故A正确； N F P F P P 学科网（北京）股份有限公司1 设Nx ,y 且x 1，则P2x 1,2y ，代入得x2  y2  ， N N N N N N N 4 1 1 3 可得N 在以坐标原点O为圆心、 为半径的圆上运动，又圆N 交y轴于A,B，故 MN   , ，故B错误； 2 2 2 以PF 为直径的圆N 的方程可写为xx x1yyy 0， P P 令x0，可得x yyy 0，即y2 y yx 0， P P P P 则y ,y 分别为方程的两根，由韦达定理得y y  x ，故C正确； A B A B P AF 1 要证cosAFP  ，即证 PF  FA FB ， PF BF FA FB  y2 1 y2 1 y2y2   y2 y2 1 14x ， A B A B A B P PF  x 12y2  14x ， P P P 1 所以 PF  FA FB ，即cosAFP ，故D正确． BF 故选：ACD． 34．（多选题）（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）设函数 f x2x33ax21，则（ ） A．存在a，b，使得xb为曲线y f x的对称轴 B．存在a，使得点  1, f 1 为曲线y f x的对称中心 C．当a0时，xa是 f x的极大值点 D．当a1时， f x有三个零点 【答案】BCD 【解析】对于选项A，假设存在这样的a,b，使得xb为 f(x)的对称轴， 即存在这样的a,b使得 f(x) f(2bx)， 即2x33ax212(2bx)33a(2bx)21， 因为等式右边22bx3展开式含有x3的项为2C32b0x3 2x3， 3 可知等式左右两边x3的系数不相等，原等式不可能恒成立， 于是不存在这样的a,b，使得xb为 f(x)的对称轴，故A错误； 对于选项B：因为 f(1)33a， 26若存在a，使得(1,33a)为 f(x)的对称中心，则 f(x) f(2x)66a， 且 f(x) f(2x)2x33ax212(2x)33a(2x)21(126a)x2(12a24)x1812a， 126a0  可得66a(126a)x2(12a24)x1812a，则12a240 ，解得a2，  1812a66a 所以存在a2使得(1, f(1))是 f(x)的对称中心，故B正确； 对于选项C：因为 f(x)6x(xa)， 若a0，当x(a,0)时， f(x)0，当x(,a)时， f(x)0， 可知 f(x)在(a,0)内单调递减，在(,a)内单调递增， 所有 f(x)在xa处取到极大值，xa是 f x的极大值点，C选项正确； 对于选项D，由题意可知： f(x)的定义域为R，且 f(x)6x26ax6x(xa)， 因为a1，当x,0a,时， f(x)0；x(0,a)时， f(x)0； 可知 f(x)在,0,a,上单调递增，在(0,a)上单调递减， 则 f(x)在x0处取到极大值，在xa处取到极小值， 且 f(0)10， f(a)1a3 0， f 113a 0, f 2a4a31 0， 则 f(x)在,0,(0,a),a,上各有一个零点， 所以当a1时， f(x)有三个零点， 故D正确； 故选：BCD. 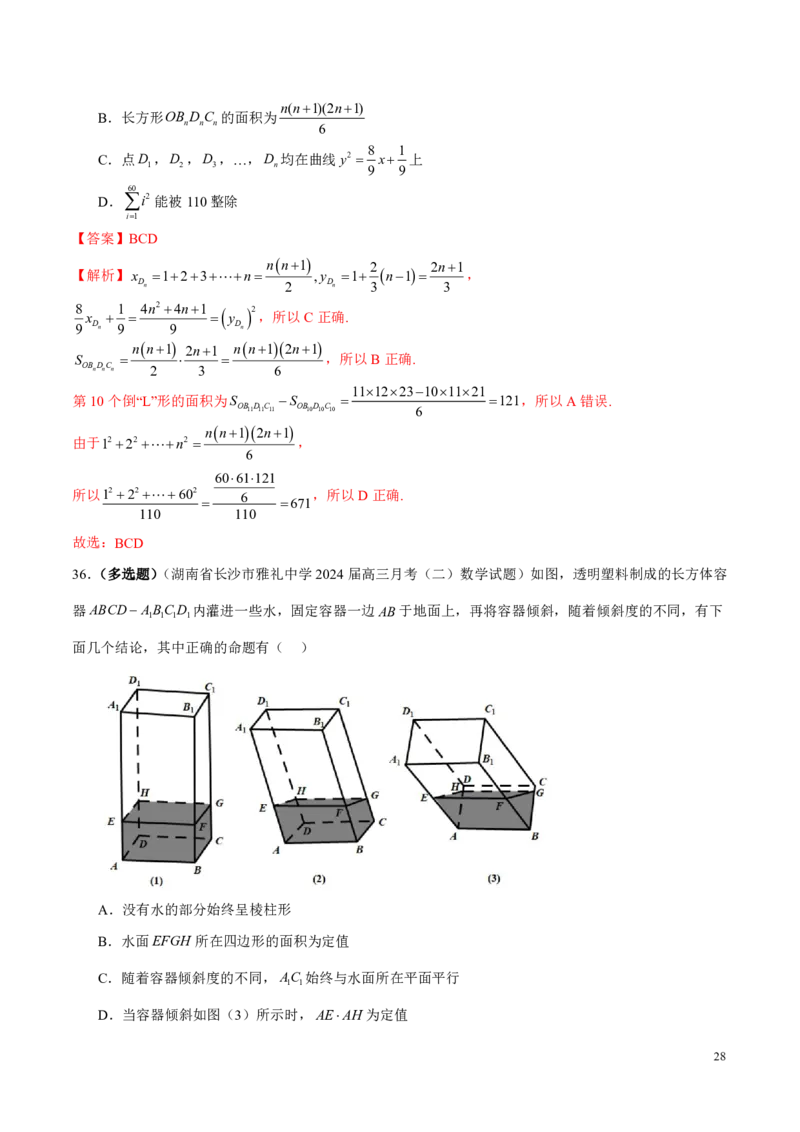35．（多选题）（广东省肇庆市肇庆中学2024届高三10月月考数学试卷）如图，在平面直角坐标系xOy中， 点B ，B ，B ，…，B 均在x轴正半轴上，点C ，C ，C ，…，C 均在y轴正半轴上．已知OB 1，BB 2， 1 2 3 n 1 2 3 n 1 1 2 2 B B 3，…，B B n(n2)，OC 1，CC C C C C  (n2)，四边形OBDC ，OB DC ， 2 3 n1 n 1 1 2 2 3 n1 n 3 1 1 1 2 2 2 OB DC ，…，OB DC 均为长方形．当n2时，记B B DC C 为第n1个倒“L”形，则（ ） 3 3 3 n n n n1 n n n n1 A．第10个倒“L”形的面积为100 学科网（北京）股份有限公司n(n1)(2n1) B．长方形OB DC 的面积为 n n n 6 8 1 C．点D ，D ，D ，…，D 均在曲线y2  x 上 1 2 3 n 9 9 60 D．i2 能被110整除 i1 【答案】BCD nn1 2 2n1 【解析】x 123n ,y 1 n1 ， Dn 2 Dn 3 3 8 x  1  4n24n1   y 2 ，所以C正确. 9 Dn 9 9 Dn nn1 2n1 nn12n1 S    ，所以B正确. OBnDnCn 2 3 6 111223101121 第10个倒“L”形的面积为S S  121，所以A错误. OB11D11C11 OB10D10C10 6 nn12n1 由于1222n2  ， 6 6061121 所以1222602 6 ，所以D正确.  671 110 110 故选：BCD 36．（多选题）（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）如图，透明塑料制成的长方体容 器ABCD ABCD 内灌进一些水，固定容器一边AB于地面上，再将容器倾斜，随着倾斜度的不同，有下 1 1 1 1 面几个结论，其中正确的命题有（ ） A．没有水的部分始终呈棱柱形 B．水面EFGH 所在四边形的面积为定值 C．随着容器倾斜度的不同，AC 始终与水面所在平面平行 1 1 D．当容器倾斜如图（3）所示时，AEAH为定值 28【答案】AD 【解析】由于AB始终在桌面上，因此倾斜过程中，没有水的部分，是以左右两侧的面为底面的棱柱，A正 确； 图（2）中水面面积比（1）中水面面积大，B错； 图（3）中AC 与水面就不平行，C错； 1 1 图（3）中，水体积不变，因此△AEH面积不变，从而AEAH为定值，D正确． 故选：AD． 37．（多选题）（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）已知奇函数 f x在R上单调递 增， fx gx，gx f x，若 f 2x2f xgx，则（ ） A．gx的图象关于直线x0对称 B．g2xg2x f2x C．g00或1 D．g2x f2x1 【答案】ABD 【解析】对于A，由 f x为 上的奇函数，则 f 00， f x f x0， 则 fx fx0，所以gxgx0，即gx为偶函数，因此关于直线x0对称，故A正确； 对于B，由 f 2x2f xgx，则两边同时求导得：2f2x2fxgx2f xgx，即 g2xg2x f2x，故B正确； 由gx f x f xgx0，则2gxgx2f x fx0，即g2x  f2x  0，即     g2x f2x  0，   则g2x f2xC（C为常数），设hxg2x f2xC（C为常数）， 对于C，由g2xg2x f2x，则g0g20 f20，即g0 g01  0，解得g00或g01， 当g00，则h0g20 f200，则hxg2x f2x0，即 f xgx， 又gx为偶函数，则 f x即是奇函数也是偶函数，与 f x在 上单调递增矛盾， 学科网（北京）股份有限公司因此g00不符合题意，则g01，故C错误； 对于D，当g01时，则h0g20 f201，则hxg2x f2x1，即g2x f2x1，故D 正确； 故选：ABD. 38．（多选题）（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）已知函数 f(x)sinxacosx(xR,0)的最大值为2，其部分图象如图所示，则（ ） A．a0  π B．函数 f x 为偶函数  6 C．满足条件的正实数存在且唯一 D． f(x)是周期函数，且最小正周期为π 【答案】ACD 【解析】由函数 f(x)sinxacosx 1a2sin(x)，且tana， 因为函数 f x的最大值为2，可得 1a2 2 ，解得a 3， 又因为 f(0)a0，所以a 3，所以A正确；  π f xsinx 3cosx2sinx   3 π π π π 因为 f  2sin  1，且函数 f x在 的附近单调递减， 4 4 3 4 π π 5 所以   π2kπ,kZ，所以28k,kZ， 4 3 6 T π π 2π π 又因为  ，可得T  ，所以  ，解得04，所以2， 2 4 2  2 π 此时 f(x)2sin(2x )，其最小正周期为T π，所以C、D正确； 3  π   π π 设Fx f x  2sin2x    2sin2x ，  6   6 3 30Fx2sin[2(x)]2sin2xFx，所以 为奇函数， π 即函数 f(x )为奇函数，所以B不正确. 6 故选：ACD. 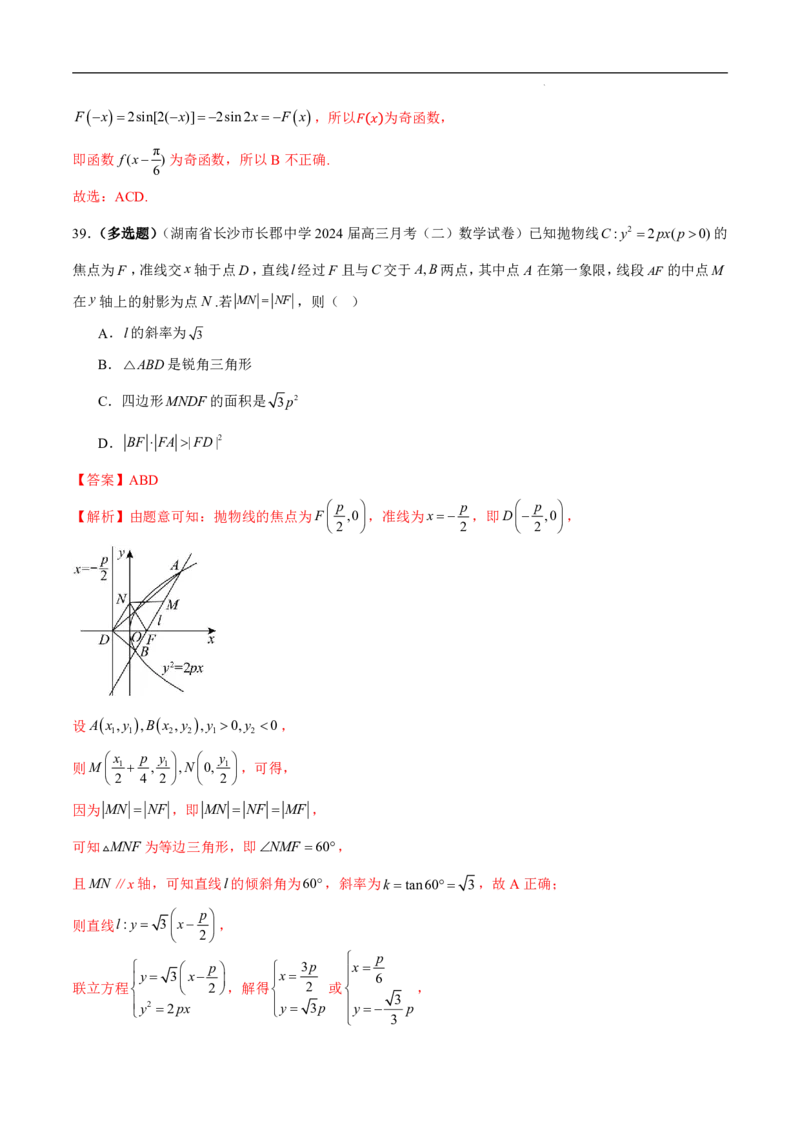39．（多选题）（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）已知抛物线C:y2 2px(p0)的 焦点为F ，准线交x轴于点D，直线l经过F 且与C交于A,B两点，其中点A在第一象限，线段AF的中点M 在y轴上的射影为点N .若 MN  NF ，则（ ） A．l的斜率为 3 B．△ABD是锐角三角形 C．四边形MNDF的面积是 3p2 D． BF  FA |FD|2 【答案】ABD  p  p  p  【解析】由题意可知：抛物线的焦点为F ,0，准线为x ，即D ,0，  2  2  2  设Ax,y ,Bx ,y ,y 0,y 0， 1 1 2 2 1 2 x p y   y  则M 1  , 1,N0, 1，可得，  2 4 2   2  因为 MN  NF ，即 MN  NF  MF ， 可知MNF为等边三角形，即NMF 60， 且MN∥x轴，可知直线l的倾斜角为60，斜率为k tan60 3，故A正确；  p 则直线l:y  3x ，  2  p  y 3  x p   x 3p   x 6 联立方程  2 ，解得 2 或 ，    3 y2 2px y 3p y p  3 学科网（北京）股份有限公司3p   p 3   3   3  即A , 3p，B  , p  ，则M  p, p  ,N  0, p  ，  2   6 3   2   2  7 2 8 可得 DF  p, AD  7p, BD  p, FA 2p, FB  p, AB  p， 3 3 3 在△ABD中， BD  AD  AB ，且 BD 2 AD 2 AB 2 0， 可知ADB为最大角，且为锐角，所以△ABD是锐角三角形，故B正确； 1 3 1 3 3 四边形MNDF的面积为S  S S   p p  p p p2，故C错误； MNDF △BDF △MNF 2 2 2 2 2 4 因为 FB  FA  p2, FD  p2，所以 BF  FA |FD|2，故D正确； 3 故选：ABD. 40．（多选题）（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）已知abc，且 2abc0，则（ ） c a A．a0,c0 B．  2 a c a2c C．ac0 D． 1 ab 【答案】ABD 【解析】对于A：因为abc，且2abc0， 若c0，则abc0，则2abc0，不合题意，所以c0； 若a0，则0abc，则2abc0，不合题意，所以a0； 综上所述：a0,c0，故A正确； 对于C：因为abc，则abac，可得2abc2ac， 即02ac，可得ac0，故C错误； 对于B：由选项AC可知：a0c，且ac0，得ac2 0， c a 即a2c2 2ac，且ac0，所以  2，故B正确； a c 对于D：因为a2cab2abccc0，可得a2cab， 又因为2abcabac0，可得abac0， a2c 所以 1，故D正确； ab 故选：ABD. 3241．（多选题）（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）设,是锐角三角 形的两个内角，且，则下列不等式中正确的有（ ） A．sinsin1 B．tantan1 1  C．coscos 2 D． tantan 2 2 【答案】ACD 【解析】因为,是锐角三角形的两个内角，且， π π π π 可得：0 ，且 ，  ， 2 2 4 2 π π π π  对于选项A：因为 ，且0  ，则sinsin cos， 2 2 2 2   π 可得sinsinsincos 2sin ，  4 π π π π 3π 2  π 因为  ，则   ，可得 sin 1， 4 2 2 4 4 2  4  π 所以sinsin 2sin 1，故A正确；  4 tantan 对于选项B：因为tan 0， 1tantan 且tan,tan0，即tantan0， 则1tantan0，即tantan1，故B错误； π π  对于选项C：因为 ，则coscos sin， 2 2   π 则coscoscossin 2sin  ，  4 2  π 由选项A可知： sin 1， 2  4  π 所以coscos 2sin   2 ，故C正确；  4  tan 对于选项D：因为 1 tan 2 ， 2  1tan2 2 π  π 又因为0 ，则0  ， 2 2 4   可得0tan 1，即01tan2 1， 2 2 学科网（北京）股份有限公司 tan 所以 1 tan 2 tan  ，故D正确； 2  2 1tan2 2 故选：ACD 42．（多选题）（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）设函数 f(x)2x33ax21， 则（ ） A．当a0时，直线y1是曲线y f(x)的切线 1 B．若 f(x)有三个不同的零点x,x ,x ，则x x x  1 2 3 1 2 3 2 C．存在a,b，使得xb为曲线y f(x)的对称轴 a D．当x  时， f x在xx 处的切线与函数y f x的图象有且仅有两个交点 0 2 0 【答案】ABD 【解析】A选项，当a0时， f x2x31， 令 fx6x2 0解得x0，且 f 01， 此时 f x在x0处的切线方程为y10，即y1，正确. B选项， f(x)2x33ax21, fx6x26ax6xxa， 要使 f x有三个零点，则a0， 若 f(x)2x33ax21有三个不同的零点x,x ,x ， 1 2 3 则 f x2xx xx xx  1 2 3 2x32x x x x2xx x x xx x2xx x ， 1 2 3 1 2 2 3 1 3 1 2 3 1 通过对比系数可得2xx x 1 xx x  ，正确. 1 2 3 1 2 3 2 C选项，若存在a,b，使得xb为曲线y f(x)的对称轴， 则 f x f 2bx，即2x33ax2122bx33a2bx21， 即2x33ax2 16b324b2x12bx22x312ab212ab3ax2， 即x33bx26b2x  4b23ab3a  b0，此方程不恒为零， 所以不存在符合题意的a,b，使得xb为曲线y f(x)的对称轴，错误. 34a D选项，当x  时， f(x)2x33ax21, fx6x26ax， 0 2 则 f(x )2x33ax21, fx 6x26ax ， 0 0 0 0 0 0 所以 f x在xx 处的切线方程为y  2x33ax21    6x26ax xx ， 0 0 0 0 0 0 y  6x26ax xx   2x33ax21  ， 0 0 0 0 0  y  6x26ax xx   2x33ax21  由 0 0 0 0 0 ， y2x33ax21 消去y得2x33ax212x33ax21  6x26ax xx ①， 0 0 0 0 0 由于2x32x3 2  x3x3 2xx  x2xx x2 ， 0 0 0 0 0 3ax23ax2 3a  x2x2 3axx xx ， 0 0 0 0 所以①可化为2xx  x2xx x2 3axx xx   6x26ax xx 0， 0 0 0 0 0 0 0 0 提公因式xx 得xx 2  x2xx x2 3axx   6x26ax 0， 0 0  0 0 0 0 0  化简得xx 2x22x 3ax  4x23ax 0， 0  0 0 0  3a4x 进一步因式分解得xx 22x4x 3a0，解得x x ,x  0 ， 0 0 1 0 2 2 a 由于x  ，所以2x -a¹0， 0 2 0 3a4x 6x 3a 32x a 所以x x  x  0  0  0 0，所以x x ， 1 2 0 2 2 2 1 2 a 所以当x  时， f x在xx 处的切线与函数 的图象有且仅有两个交点，正确. 0 2 0 故选：ABD = 43．（多选题）（湖北省新八校协作体2023-2024学年高三10月联考数学试题）设函数 f x的定义域为R，  π f x 为奇函数， f xπ为偶函数．当x0,π时， f xcosx，则下列结论正确的有（ ）  2 7π A． f x在3π,4π上单调递减 B． f  0  2   5  C．点 π,0是函数 f x的一个对称中心 D．方程 f xlgx0有5个实数解  2  【答案】BCD  π  π  π 【解析】因为 f x 为奇函数，所以 f x f x ，即 f xf xπ，  2  2  2 学科网（北京）股份有限公司因为 f xπ为偶函数，所以 f xπ f xπ， 所以 f(xπ)f(x)，即 f(xπ)f(x) f(x2π) f(x)，则 f(x)周期为2π， 由 f xπ f xπ得， f(x)的一条对称轴为直线xπ， 因为当x 0,π 时， f xcosx，所以当xR时， f xcosx， 对于A， f x在π,2π上单调递增，所以 f x在3π,4π上单调递增，故A错误； 7π 7π 对于B， f  cos 0，故B正确；  2  2  5   5   5  对于C，由 f  πcos π0得，点 π,0是函数 f x的一个对称中心，故C正确；  2   2   2  对于D，在同一直角坐标系中作出ycosx,ylgx的图象，如图所示， 因为ycosx与ylgx有5个交点，所以方程 f xlgx0有5个实数解，故D正确； 故选：BCD． 44．（多选题）（湖北省新八校协作体2023-2024学年高三10月联考数学试题） 表示不超过x的最大整数， 例如，[0.5]1， 1.1 1，已知函数 f x x ，下列结论正确的有（ ） 1  1 A．若x0,1，则 f x   f x  4  4 B． f xy f x f y C．设gx f  2 5x   f   x2  ，则 20 gk401 20 k1   14 40 D．所有满足 f m fn m,n  0, 的点m,n组成的区域的面积和为   3  9 【答案】AD 【解析】A选项，由题x0,1时， f x0， f x1， 1 1 3  1 则 f x 1  0  f x  ，故A正确； 4 4 4  4 36B选项，取x2.5，y3.5，则 f xy f 665 f 2.5 f 3.5， 故B错误； C选项， 5 2.2362 5 4.472，则当x0时， f  2 5x   f 4x， 则 20 f  2 5k   20 f 4k4880 (480)20 840， 2 k1 k1 又 f   x2  0，则 20 gk 20 f  2 5k   20 f   k2  840 401 ，故C错误； 20 k1 k1 k1 20 D选项，由题要使 f m f n，则m,n 0,1，或m,n 1,2，或m,n 2,3，  14 或m,n 3,4，或m,n 4, ，所表示区域如下图阴影部分所示：    3  2 则m,n区域面积为：4   14 4    40 ，故D正确.  3  9 故选：AD 45．（多选题）（河南省七校联考2024届高三第二次联合教学质量检测数学试题）已知函数 f x的定义域 为R，且满足 f x f y f x y2xy1, f 13，则下列结论正确的是（ ） A． f 421 B．方程 f xx有整数解 C． f x1是偶函数 D． f x1是偶函数 【答案】A 【解析】对于A，因为函数 f(x)的定义域为R，且满足 f(x) f(y) f(x y)2xy1, f(1)3， f(0)1 取x y0，得： f(0) f(0) f(0)01，则 f(0)1 取x y1，得 f(1) f(1) f(2)21，则 f(2)7， 取x y2，得 f(2) f(2) f(4)81，则 f(4)21，故A正确； 对于B，取y1，得 f(x) f(1) f(x1)2x1，则 f(x1) f(x)2x2， 学科网（北京）股份有限公司当 时，有： f( x)>1f(x1)2(x1)2, f(x1) f(x2)2(x2)2,, f(2) f(1)22， 以上各式相加得 f x f 1  2x12  x1 2x1x2x2x1x2x2， 2 所以 f xx2x1,x1， 而 f x f x22x2，故当x1时，有 f x22x2 f xx2x1 x2x1,x1  所以 f x3,x1 ,  1,x1  所以当x1时，令 f(x) x2x1 x，得x22x10，此方程无解， 当x1时，31，也无解，当 时，11，也无解，故B错误. 对于C,若 f x1是偶函数，则 应 = 有 −1 f 0 f 2，而 f 01 f 27，故C错误; 对于D,若 是偶函数，则应有 f 0 f 2， 由 f(x) f (y ) −1 f(x y)2xy1,， f(0)1， f(2)7 取x2,y2，得 f(2) f(2) f(0)81,所以 f(2)3 而 f 01 f 23，故D错误; 故选：A 46．（多选题）（河南省七校联考2024届高三第二次联合教学质量检测数学试题）如图，在长方体 1 ABCDABCD中，ABBC2，AA4，N 为棱CD中点，DM  ，P为线段AB上一动点，下列结 2 论正确的是（ ） 6 5 A．线段DP长度的最小值为 5 B．存在点P，使APPC 2 3 38C．存在点P，使AC平面MNP 17 D．以B为球心， 为半径的球体被平面ABC所截的截面面积为6π 6 【答案】AC 【解析】选项A，由已知BD2 2，AD AB2 5，如图1， 2 10 3 10 ABD是等腰三角形，cosABD  ，则sinABD ， 2 5 10 10 3 10 6 5 所以边AB上高为BDsinABD 2 2  ，A正确； 10 5 选项B，把矩形ABCD沿AB摊平到平面ABA上，如图2 4 2 5 π 2 5 sinABA  ，则cosABC cos(ABA  )sinABA  ， 2 5 5 2 5 2 5 4 5 4 5 AC  2222222( )2 2 ，这是APPC的最小值，显然2 3，即 5 5 5 4 5 2 2 2 3，因此B错； 5 选项C，连接CD，设CDMN Q，在平面ABCD上过Q作QP AC交AB于点P，如图3， 学科网（北京）股份有限公司1 π 长方体中易知AB//CD，由已知DM  ，DN 1，又DD4,DC2且MDN DDC ， 2 2 因此 DDC DNM ，则DNM MDQ， π 所以DMQMDQDMQDNM  ，所以DCMN， 2 又长方体中BC与侧面DCCD垂直，MN 侧面DCCD，因此BCMN， BC与CD是平面BCDA内两条相交直线，因此MN 平面BCDA，又AC 平面BCDA，所以MN  AC， PQMN Q，且PQ,MN 平面PMN，所以AC平面PMN，C正确； 选项D，设ACBDO，连接OB，作BH OB，垂足为H，如图4， 由BB 平面ABCD，AC平面ABCD得BB AC， 又正方形ABCD中，ACBD， BDBB  B ，BD,BB平面BDDB， 所以AC平面BDDB，而BH 平面BDDB，所以ACBH， ACBO O，AC,BO 平面ABC，所以BH 平面ABC， 4 2 4 由已知BO 2，BB4，则BH   ， 42( 2)2 3 17 4 5 平面ABC截球所得截面圆半径为r，则r ( )2( )2  ， 6 3 2 5 25π 所以截面圆面积为S π( )2  ，D错． 2 4 40故选：AC． 47．（多选题）（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知函数 1 f(x)sin2x ，则（ ） sinxcosx A． f(x)为奇函数 B． f(x)的值域为(,2 2][2 2,) 3π C． f(x)的图象关于直线x 对称 4 D． f(x)以π为周期 【答案】ACD 2 【解析】 f xsin2x ， sin2x kπ  kπ  sin2x0，则2xkπx ，kZ，则函数的定义域为x x ,kZ，函数的定义域关于原点对称， 2  2  且满足 f xf x，所以函数是奇函数，故A正确； 2 设tsin2x1,0  0,1 ，yt 在区间0,1 单调递减，y 3,，因为函数是奇函数，所以函数的值 t 域是,3  3,，故B错误； f   3π x  sin3π2x 2  sin2x 2  f x  ，所以函数 f x关于x 3π 对称，故C正确；  2  sin 3π2x sin2x 4 2 2 f xπsin2x2π sin2x2π sin2x sin2x  f x ，所以函数 f x的周期为π，故D正确. 故选：ACD 48．（多选题）（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知对任意x0，不等 式exax32ax2lnx0恒成立，则实数a的可能取值为（ ） e A．1 B． C．e D．e2 2 【答案】ABC ex 【解析】由x0，exax32ax2lnx0可化为 ax2alnx0， x2 则又可化为 ex a  xlnx2 0 ex aln ex 0， x2 x2 x2 ex ex(x2) 令(x) ，则(x) ，令(x)0，得x2， x2 x3 学科网（北京）股份有限公司当0x2时，(x)0，则(x)在(0,2)单调递减； 当x2时，(x)0，则(x)在(2,)单调递增； e2 故(x) (2) ，且当x，(x). min 4 ex e2  再令t  ，则t  ,， x2  4  e2  则关于t的不等式talnt0在 ,恒成立，  4  t e2  即a 在 ,恒成立， lnt  4  t e2  令h(t) ，t  ,， lnt  4  lnt1 则h(t) ，由h  (t)0解得te， (lnt)2 e2 e2  当 te时，h(t)0，则h(t)在 ,e单调递减； 4  4  当t e时，h(t)0，则h(t)在(e,)单调递增； 所以h(t) h(e)e， min t e2  要使a 在 ,恒成立，则ae. lnt  4  故选：ABC. 1 49．（多选题）（河南省部分名校2023-2024学年高三10月月考数学试卷）已知函数 f x 1，则下列 lnx 说法正确的是（ ） A． f x的图象无对称中心 1 B． f x f   2 x 1 C． f x的图象与gx 1的图象关于原点对称 lnx D． f x的图象与hxex1的图象关于直线y x对称 【答案】BC 42【解析】选项A，由已知 f(x)的定义域是{x|x0且x1}， 假设 f x的图象有对称中心(x ,y )，取P(x,y)，其中x2x ，P关于点(x ,y )的对称点是Q(2x x,2y y)， 0 0 0 0 0 0 0 但2x x不在 f(x)的定义域内，即Q不是 f(x)图象上的点，与对称性矛盾，因此假设错误，所以A正确； 0 1 1 1 1 1 f(x) f( ) 1 1  22 选项B， x lnx 1 lnx lnx ，B正确； ln x 选项C，设P(x,y)是 f(x)图象关于原点对称的图象上任一点，它关于原点的对称点为Q(x,y)在 f(x)的 图象上， 1 1 因此y 1，即y 1， ln(x) ln(x) 所以 f(x)的图象上任一点关于原点的对称点在g(x)的图象上， 同理可证g(x)的图象上任一点关于原点的对称点都在 f(x)的图象上，C正确； 选项D，由y ln 1 x 1得lnx y 1 1 ， xey 1 1 ，所以 f(x)的图象关于直线y x对称的图象的函数式为 yex 1 1 ， D错， 故选：BC． 1 50．（多选题）（河南省部分名校2023-2024学年高三10月月考数学试卷）记函数 f xex  的零点为x ， x 0 则下列说法正确的是（ ） A．x lnx 0 0 0 1 3 B．x  ,  0 2 4 3 C．当x 时， f x x1 2 1 D．x 0 为函数 gx ex xlnx的极值点 x1 【答案】BC 1 1 【解析】A选项，由题ex0  0ex0   x lnx  x lnx 0，故A错误； x x 0 0 0 0 0 0 1 B选项， fxex  0，则 f x在 上单调递增，即 f x在 上有唯一零点x . x2 0 1 1 3 3 4 0,+∞ 03,+∞ 3 又 f  e2 20， f  e4  ，因e2.718，则e3 2.7183 16e4 2 f  0. 2 4 3 4 1 3 则由零点存在性定理，x  , ，故B正确； 0 2 4 学科网（北京）股份有限公司1 C选项，令hx f xx1ex x 1， . x 1 ∈ 0,+∞ 则gxex 1 0，得gx在 上单调递增， x2 3 3 19 0,+∞ 3 3 h e2  ，由B选项分析e3 2.7183 16e2 4h 0， 2 6 2 3 3 则当x 时，hx f xx1h 0 f x x1，故C正确； 2 2  1 1 y 1 1  1 1 1 D选项，设yex lny ，两边求导得   y yex  ex. x y x2 x2   x2  1 1  1  1 1  1 1  ex xlnx1 1  ex0 x lnx 1 则 gx  x x2  ， gx   x 0 x 0 2  0 0 . x12 0 x 12 0  1 1  1  1 1  1 由A选项分析， 1  ex0 x lnx 11  ex01 ，  x x 2  0 0  x x 2  0 0 0 0 又ex0  1 ，则ex0 x 1， 1 e2x0    ex0x ex0 e2x0  e 1 x0    x  1 1   e x0  1 x0. x 0 0 x 0 2 0  0 x 0  又由B分析，x 0  x 1 2 x 0  x 1 2 x 0  x 1 13，又 e x0  x 1 0 1 ，则    x 0  x 1 1    e x0  x 1 0 3， 0 0 0 0  1 1  1 1 得  1 x 0  x 0 2   ex0 120，则x 0 不为函数 gx ex x   x 1 lnx的极值点，D错误. 故选：BC 51．（多选题）（河南省部分名校2024届高三月考（一）数学试题）已知定义在实数集R上的函数 f x， 1 其导函数为 fx，且满足 f x y f x f yxy， f 10, f1 ，则（ ） 2 A． f x的图像关于点1,0成中心对称 3 B． f2 2 C． f 202410122023 2024 D．  f(k)10122024 k1 【答案】BCD 【解析】对A：令x y0，则有 f 0 f 0 f 00，即 f 00， 44令x y1，则有 f 2 f 1 f 11，又 ，故 f 21， f x不关于 对称，故A错误； 1 =0 1,0 对于B，令y1，则有 f x1 f x f 1x f xx， 两边同时求导，得 fx1 fx1， 1 3 令x1，则有 f2 f11 1 ，故B正确； 2 2 对C：令y1，则有 f x1 f x f 1x，即 f x1 f xx， 则 f 2024 f 2024 f 2023 f 2023 f 2022 f 1 f 1 202312023 2023202210 10122023，故C正确； 2 对D：令y1，则有 f x1 f x f 1x，即 f x1 f xx， 则 fx1 fx1，即 fx1 fx1， 1 1 1 又 f1 ，故 fk k1k ， 2 2 2 1 1  2024 2024 则2  024 fk 2 2 10122024 ，故D正确. 2 k1 故选：BCD. π 52．（多选题）（河南省部分名校2024届高三月考（一）数学试题）设函数 f(x)的定义域为R， f(x )为 4 π π π 4 奇函数， f(x )为偶函数，当x( , ]时， f(x)cos x，则（ ） 4 4 4 3 3π A． f(x4π) f(x) B． f(x)的图象关于直线x 对称 4 3π C． f(x)在区间( ,2π)上为增函数 D．方程 f(x)lgx0仅有4个实数解 2 【答案】ACD π π 【解析】因为 f(x )为奇函数，所以 f(x)的图象关于点( ,0)中心对称， 4 4 π π 因为 f(x )为偶函数，所以 f(x)的图象关于直线x 对称． 4 4 π 可画出y f(x)的部分图象大致如下（图中x轴上相邻刻度间距离均为 ）： 4 学科网（北京）股份有限公司对于A，由图可知 f(x)的最小正周期为2π，所以 f(x4π) f(x)，故A正确． 3π 对于B， f(x)的图象关于点( ,0)中心对称，故B错误． 4 3π 对于C，由图可知 f(x)在区间( ,2π)上单调递增，故C正确． 2 3π 5 1 7π 1 5π 对于D，lg lg  ，lg lg5 ，lg 1，lg4πlg101， 4 2 2 4 2 2 由图可知，曲线ylgx与y f(x)的图象有4个交点，所以方程 f(x)lgx0仅有4个实数解，故D正确． 故选：ACD. 53．（广东省五校2023-2024学年高三10月联考（二）数学试题）已知函数 f(x)的定义域为(0,)，其导 函数为 f(x)，若xf(x)10. f(e)2，则关于x的不等式 f(ex) x1的解集为 . 【答案】(1,) 1 xf(x)1 【解析】令函数g(x) f(x)lnx,x0，则g(x) f(x)  0，因此函数g(x)在(0,)上单调 x x 递减， g(e) f(e)lne1，因此 f(ex) x1 f(ex)x1 g(ex) g(e)，即ex e，解得x1， 所以不等式 f(ex) x1的解集为(1,). 故答案为：(1,) 54．（广东省七校2024届高三第二次联考数学试卷）已知函数 f(x) 3x1 ，数列a 满足a 1，a 2， 3x1 n 1 2 a a  nN* ， f a  f a a 0，则 2  024 a  . n3 n 2 3 4 i i1 【答案】3 【解析】由题意可知： f(x)的定义域为R， 3x1 3x1 3x1 13x 且 f(x) f(x)    0，即 f(x)f(x)， 3x1 3x1 3x1 13x 可知 f(x)为定义在R上的奇函数； 3x1 2 且 f(x) 1 ， 3x1 3x1 因为y3x在R上单调递增，可知 f(x)在R上单调递增； 46综上所述： f(x)在R上单调递增，且为奇函数. 因为 f a  f a a 0，则 f a a f a  f a ， 2 3 4 3 4 2 2 可得a a a ，即a a a 0， 3 4 2 2 3 4 由a a  nN* 可知：3为数列a 的周期，则a a a 0， n3 n n n n1 n2 2024 且202436742，所以a a a 3. i 1 2 i1 故答案为：3.  π 55．（广东省七校2024届高三第二次联考数学试卷）函数 f x8lnsinxsin22x在区间0, 上的零点个  2 数为 个． 【答案】0 【解析】 f x8lnsinxsin22x8lnsinx1cos22x 8lnsinx1(12sin2x)2 8lnsinx4sin2x4sin4x， 令tsinx(0,1)，则 f(t)8lnt4t24t4， 8 88t216t4 8(2t21)(1t2) 则 f(t) 8t16t3   0， t t t 所以 f(t)在(0,1)上单调递增，所以 f(t) f(1)8ln1412414 0，  π 所以函数 f x8lnsinxsin22x在区间0, 上的零点个数为0个.  2 故答案为：0. 56．（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知正数a,b满足2a1b14，则ab 的最小值为 ． 3 【答案】2 2  2 4 2 1 【解析】由题意可得2a1 ，故a  ，又b0， b1 b1 2 2 1 2 3 2 3 3 所以ab  b b1 2 b1  2 2 ， b1 2 b1 2 b1 2 2 2 1 当且仅当 b1，即b 21,a 2 时取等号． b1 2 3 故答案为：2 2  ． 2 学科网（北京）股份有限公司sinacos cos3 57．（广东省（上进联考）2024届高三10月阶段检测考数学试题）若关于的方程  在 cosasin sin3  π 区间0, 上有且仅有一个实数解，则实数a ．  4 【答案】2 2 【解析】等号左边的分子和分母同时除以cos，等号右边的分子和分母同时除以cos3， 1tan4 分离出参数a (0tan1)， tan3tan x41  x21  x44x21  设 f x (0 x1), fx ， x3x  x3x 2  31 则当x0, 时， fx0, f x单调递增，  2   31  当x ,1时， fx0, f x单调递减，  2  且x0时， f x,x1时， f x，且方程有唯一解，  31 1(2 3)2 a f   2 2 故  2  31   ．  2 31 2 故答案为：2 2. x2 y2 58．（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）椭圆  1ab0的离 a2 b2 51 x2 y2 心率e满足e ，则称该椭圆为“黄金椭圆”．若  110m0是“黄金椭圆”，则m ； 2 10 m “黄金椭圆”C: x2  y2 1ab0两个焦点分别为Fc,0、F c,0（c0），P为椭圆C上的异于顶点 a2 b2 1 2 PM 的任意一点，点M是PFF 的内心，连接PM并延长交FF 于N，则  ． 1 2 1 2 MN 51 【答案】 5 55 2 x2 y2 51 10m 【解析】因为  110m0是“黄金椭圆”，故  ，故m5 55， 10 m 2 10 48连接F M,FM ，因为M 为内心，故F M,FM 为角平分线， 2 1 2 1 PF PM PF PF  PF PM 2a a 2 51 由角平分线性质，有 2   1 ，故 2 1      ， NF NM NF NF  NF NM 2c c 51 2 2 1 2 1 51 故答案为：5 55， . 2 59．（广东省肇庆市肇庆中学2024届高三10月月考数学试卷）若存在实数t，对任意的x∈(0，s]，不等式(lnx －x＋2－t)(1－t－x)≤0成立，则整数s的最大值为 ．(ln3≈1.099，ln4≈1.386) 【答案】2 【解析】令 f(x)lnxx2，g(x)1x， 1 [f(x)t][g(x)t]0， f(x) 1， x 令 f(x)0x1， ∴当0x1时， f(x)0 ， f(x)单调递增； 当x1时， f(x)0， f(x)单调递减，  f(x)  f(1)1，分别作出 f(x)，g(x)大致图象如下： max ylnxx2 1 1 1 联立  x ，即A ,1 ， y1x e e e 1 1 设B(x ,y )，0s x ，令lnxx21 ，即lnxx1 0， 0 0 0 e e 1 令h(x)lnxx1 ，知h(x)在(1,)上单调递减， e 学科网（北京）股份有限公司1 1 1 1 1 h(2)ln221 0.307 0，h(3)ln32 1.0992 0.901 0， e e e e e x (2,3)，∴整数s的最大值为2． 0 故答案为：2 60．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）如图，VABC中，AB6，AC2BC，D 为AB中点，则tanBDC的取值范围为 .  4 【答案】0,   3 【解析】 以D为坐标原点，AB所在的直线为x轴，AB的中垂线为y轴建立如图所示的平面直角坐标系， 则A3,0，D0,0，B3,0， 设Cx,y，又AC2BC，则C在第一象限或者第四象限，结合对称性，不妨设C在第一象限， 则 x32y2 2 x32y2 ，整理得x52 y2 16且y0， y 又tanBDC ，结合图象知，tanBDC 0， x y2 x210x9  1 2 1 则tan2BDC   9  10 1， x2 x2  x x 1 5 16 当  时，tan2BDC取最大值为 ， x 9 9 4  4 则0tanBDC ，即tanBDC的取值范围为0,  ， 3  3  4 故答案为：0, .  3 61．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）小军和小方两人先后在装有若干黑球的黑 50盒子与装有若干白球的白盒子（黑球数少于白球数）轮流取球，规定每次取球可以从某一盒子中取出任意 多颗（至少取1颗），或者在两个盒子中取出相同颗数的球（至少各取1颗），最后不能按规则取的人输.已知 两盒中共有11个球，且两人掷硬币后决定由小军先手取球.小方看了眼黑盒中的球，对小军说：“你输了！” 若已知小方有必胜策略，则黑盒中球数为 . 【答案】4 【解析】设黑球数为m，白球数为n，由mn11，mn，则m,n可能有以下几种情况： ①1,10，小军可先手在白盒子中取8颗球，此时两盒球数为1,2，则小方必不可能全部取完，小方后手取 球后可能为 ， ，1,1， ，此时无论何种情况小军都可全部取完，故小军有必定获胜的策略， 0,2 0,1 1,0 不符合题意； ②2,9，小军可先手在白盒子中取8颗球，此时两盒球数为 ，同①进行分析可知，小军有必定获胜的 2,1 策略，不符合题意； ③3,8，小军可先手在白盒子中取3颗球，此时两盒球数为3,5，小方取球后，若两盒中球数一样或有一 盒取空，则小军可全部取完，小军必胜； 若两盒中球数不一样，且均不为0，则一定是以下三种情况之一： （1）两盒球数为3,4； （2）有一盒中只有一个球，另一盒中多于两个球，即1,3，3,1，1,5； （3）有一盒中有两个球，另一盒中多于两个球，即2,4，3,2，2,5； 无论为哪种情况，小军都可将其取为1,2或 ，知此时小军必胜，不符合题意； 2,1 ④4,7，若小军只从白盒中取球， 则两盒球数为4,1，4,2，4,3时，由③的推理过程知，小方必胜；符合题意. 若两盒球数为4,6时，小方可将球数转为3,5，知小方必胜； 若两盒球数为4,5时，小方可将球数转为1,2，知小方必胜； 若两盒球数为4,4时，知小方必胜 若小军从黑盒中取出了球，则黑盒中球数3，白盒中球数黑盒中球数3，从而由③推理过程知小方必胜； ⑤5,6，小军可将球数转化为1,2，小军必胜，不符合题意； 学科网（北京）股份有限公司因此小方有必胜策略，则黑盒中球数为4， 故答案为：4. 62．（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）小澄玩一个游戏：一开始她在2个盒子A,B 中分别放入3颗糖，然后在游戏的每一轮她投掷一个质地均匀的骰子，如果结果小于3她就将B中的1颗糖 放入A中，否则将A中的1颗糖放入B中，直到无法继续游戏．那么游戏结束时B中没有糖的概率 是 ． 1 【答案】 17 【解析】设A中有k颗糖，B中有6k颗糖，游戏结束时B中没有糖的概率为a k 0,1,,6 . k 1 2 1 1 2 显然a  a ，a  a  ,a  a  a 1k 5， 0 3 1 6 3 5 3 k 3 k1 3 k1 可得a a 2a a ，则a a 25a a 26a ， k1 k k k1 6 5 1 0 0 a a 26a a 25a 26a a 22a 26a   27 1  a ， 6 5 0 4 0 0 1 0 0 0 同理a a 22a 25a   261  a ， 5 1 0 0 0   27 1  a  2 261  a  1 ，解得a  1  1 0 3 0 3 0 385 255 a   241  a 15 1  1 . 3 0 255 17 1 故答案为： 17 63．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）在如图所示的直角梯形ABCD    中，AB∥CD,AB1,BCCD2,ABBC.P为梯形ABCD内一动点，且AP1，若APABAD，则   的最大值为 . 2 5 【答案】 /1.25 4 【解析】如图，以A为坐标原点，建立平面直角坐标系， 52则A0,0,B1,0,D1,2， 1 π 且AP1，可知点P在标准单位圆上，可设Pcos,sin,0,tan ,πα ， 2 2    可得APcos,sin,AB1,0,AD1,2，    若APABAD,2，  1 cos sin cos   2 可得 ，解得 ， 2sin  1 sin  2   1  1 3 5 则 cos sin sincos sin cos， 2  2  4 4 4 4 3  π 其中cos ,sin ,0, ， 5 5  2 3 4 当且仅当2π，即2π，sinsin ,coscos 时， 5 5  5 cos1，此时为第四象限角，符合题意， 取到最大值 2 4 5 故答案为： . 4 64．（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）掷一个质地均匀的骰子，向上的点数 不小于3得2分，向上的点数小于3得1分，反复掷这个骰子，（1）恰好得3分的概率为 ；（2） 恰好得n分的概率为 ．（用与n有关的式子作答） 13 3 4  2 n1 【答案】    27 5 15  3 4 2 【解析】（1）掷一个质地均匀的骰子，向上的点数不小于3的概率  , 6 3 2 1 掷一个质地均匀的骰子，向上的点数小于3的概率  . 6 3 因为一次得2分，另一次得1分或三次得1分时恰好得3分， 2 1 1 2 12 1 13 所以恰好得3分的概率等于C1   +C0  = = . 2 3 3 3 3 27 27 学科网（北京）股份有限公司（2）令P表示“恰好得n分”的概率，不出现n分的唯一情况是得到n1分以后再掷出一次不小于3的情况， n 因为“不出现n分”的概率是1P ，所以“恰好得到n1分”的概率是P . n n1 2 2 因为“掷一次得2分”的概率是 ，所以有1P  P ， 3 n 3 n1 2 即P  P 1，则构造等比数列P ， n 3 n1 n 2 2 5 5 3 设P  P ，即P  P  ，则 1， ， n 3 n1 n 3 n1 3 3 5 3 2 3 所以P   P  ， n 5 3 n1 5 1 3 1 3 4  3 4 2 又P  ，P     ，所以P  是首项为 ，公比为 的等比数列， 1 3 1 5 3 5 15  n 5 15 3 n1 n1 3 4  2 3 4  2 即P     ，P     . n 5 15  3 n 5 15  3 n1 3 4  2 故恰好得n分的概率为    . 5 15  3 13 3 4  2 n1 故答案为：（1） ；（2）    . 27 5 15  3 65．（湖北省新八校协作体2023-2024学年高三10月联考数学试题）任意一个三次多项式函数 f xax3bx2cxd的图象都有且仅有一个中心对称点为  x，f x  ，其中x 是 的根， 0 0 0 ″ ″ =0 是 的导数.若函数 f xx3 px2xq图象的中心对称点为1，2，存在x1,，使得 ' ex mxelnx1  f xx33x2e  xe成立，则m的取值范围为 . 【答案】[e,) 【解析】 f xx3 px2xq， f(x)3x22px1， f(x)6x2p， 又 f(x)的图象的对称中心点(1,2)， f(1)62p0 p3 所以 ，解得 ，所以 f(x) x33x2x1， f(1)1 p1q2 q1 不等式ex mxelnx1f xx33x2exe为exmxelnx1(x1e)xe，   exelnx (x1e) 因为x(1,)，所以m ， lnx1 令g(t)et t1，则g(t)et 1， 54当t0时，g(t)0，g(t)递减，t0时，g(t)0，g(t)递增， 所以g(t) g(0)0，所以et t1， 从而exelnx xelnx1，当且仅当xelnx0，即xe时等号成立， exelnx (x1e) xelnx1(x1e) exelnx (x1e) 所以  e，所以 的最小值是e， lnx1 lnx1 lnx1 所以me． 故答案为：[e,)． 66．（河南省七校联考2024届高三第二次联合教学质量检测数学试题）南宋数学家杨辉为我国古代数学研 究做出了杰出贡献，他的著名研究成果“杨辉三角”记录于其重要著作《详解九章算法》，该著作中的“垛积术” 问题介绍了高阶等差数列，以高阶等差数列中的二阶等差数列为例，其特点是从数列的第二项开始，每一 项与前一项的差构成等差数列.若某个二阶等差数列的前4项为1，3，7，13，则该数列的第15项为 ． 【答案】211 【解析】设数列为a  ,根据题意a a 2,a a 4,,a a 2n1,n2， n 2 1 3 2 n n1 n122n2 则累加可得a a 242n1 nn1, n 1 2 所以a n2n1，故a 211. n 15 故答案为：211. 67．（河南省七校联考2024届高三第二次联合教学质量检测数学试题）在平面直角坐标系xOy中，A、B分 别为x、y轴上的点，2OA  OB ，则以原点为顶点且经过A、B两点的抛物线的准线斜率为 . 【答案】  1 2 3 【解析】设抛物线C:y2 2px， OB 2a， OA a，BOx，BOy，如图所示， 1 1 1 1  π  π  则B 2acos,2asin，A acos ,asin ，即A asin,acos， 1 1  2  2  1 学科网（北京）股份有限公司4a2sin2 4pacos 又A,B 在C上 ， 1 1 a2cos22pasin 1 1 tan3 ，故tan 3 ， 2 2 π  π 又 ，,0, ，所以tan 3 2， 2  2 故逆时针旋转后,A,B 分别旋转到x,y轴上的点A,B， 1 1 1 此时抛物线对称轴斜率为tan 3 2，而准线与对称轴垂直，故 k 2  3. l 故答案为：  1 . 2 3 68．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知a,b均为正实数，且2a3bab， 1 3 则  的最小值为 . a3 b2 【答案】 2 【解析】由2a3bab，得ab2a3b0， 则ab2a3b6(a3)(b2)6， 由已知a0,b0，则2aab3bb(a3)0，所以a3， 且3bab2aa(b2)0，所以b2. 所以a30,b20， 1 3 1 3 3 故  2  2  2， a3 b2 a3 b2 6 1 3 当且仅当  ，即a3 2,b23 2时等号成立， a3 b2 1 3 所以  的最小值为 2 a3 b2 故答案为： 2. 69．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知曲线yex上有不同的两点P和 Q，若点P,Q关于直线y x的对称点P,Q在曲线y=kx2-x上，则实数k的取值范围为 . 【答案】0,1 【解析】曲线yex与ylnx关于直线y x对称， 又点P,Q关于直线y x的对称点P,Q在曲线y=kx2-x上， 56lnx 曲线ylnxx0与y=kx2-x有2个交点，即lnxkx2x有2个不同的实根，即方程 kx1有2个 x 不同的实根， lnx 1lnx 设函数hx ，则hx ， x x2 当0xe时， ， 在0,e上单调递增，当xe时， ， 在e,+上单调递增， ' ' ℎ1 >0 ℎ ℎ <0 ℎ hx he ，再根据当x0时，hx，当x时，hx0， max e 作出 的大致图象，如图， ℎ  lnx  由于直线ykx1过定点0,1，当直线ykx1与 的图象相切时，设切点为x , 0，此时  0 x  0 ℎ lnx 0 1 1lnx x ， k  0  0 x2 x 0 0 即2lnx x 10，可得x 1，此时切线的斜率为1， 0 0 0 由图可知，0k1时，直线ykx1与 的图象有2个交点， 实数k的取值范围为 ， ℎ 故答案为： . 0,1 70．（河南省部 0,1 分名校2023-2024学年高三10月月考数学试卷）若函数 f xsinxax的图象上存在A,B两 π 点使得 f x在A处的切线与在B处的切线的夹角为 ，则实数a的取值范围是 . 4 【答案】[ 2, 2] 【解析】 f(x)cosxa， f(x) a1， f(x) a1， max min 设斜率最大与斜率最小的两条切线的夹角为， a1(a1) 2 2 tan  ，由题意tan 1，解得 2a 2 ． 1(a1)(a1) a2 a2 故答案为：[ 2, 2]． 学科网（北京）股份有限公司a2b2 71．（河南省部分名校2023-2024学年高三10月月考数学试卷）已知ab0，则 的最小值为 . abb2 【答案】2 22 a2 1 【解析】 a2b2  b2 ，令 a tt 1，所以t10， abb2 a b 1 b 则 a2b2  t21  t12 2t  t12 2t1 2 t 1  2 22 t1 2 22 22， abb2 t1 t1 t1 t1 t1 2 a 当且仅当t1 ，即t 21，  21时取等号. t1 b a2b2 所以 的最小值为2 22. abb2 故答案为：2 22. x2 y2 72．（河南省部分名校2024届高三月考（一）数学试题）已知双曲线  1(a,b0)的左焦点为F ，过 a2 b2   2π 坐标原点O作直线与双曲线的左右两支分别交于A,B两点，且 FB 4FA,AFB ，则双曲线的渐近线 3 方程为 ． 2 【答案】y x 3 【解析】双曲线的右焦点为F ，连接AF ,BF ， 2 2 2 由A,B关于原点对称，F,F 也关于原点对称，可知四边形FAFB是平行四边形， 2 2   2π   π 又 FB 4 FA ，AFB ，则有 FB 4F B ，FBF  ， 3 2 2 3    8a  2a 又由双曲线的定义得 FB  F B 2a，解得 FB  , F B  ， 2 3 2 3 再由余弦定理：FF2 FB2FB22FBFBcosFBF ， 2 2 2 2 64 4 8 2 π 52 c2 13 即4c2  a2 a22 a acos  a2，得  ， 9 9 3 3 3 9 a2 9 b c2a2 13 2 再由   1 ， a a2 9 3 2 故渐近线方程为：y x， 3 582 故答案为：y x. 3 学科网（北京）股份有限公司