答案_2024年5月_01按日期_11号_2024届浙江省县域教研联盟高三下学期二模_浙江省县城教研联盟2023-2024学年高三下学期模拟考试数学试题

2023-2024 学年第二学期浙江省县域教研联盟高三年级模拟考试 数学参考答案 一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题 目要求的。 题号 1 2 3 4 5 6 7 8 答案 B D C A B C A B 1．因为A(4,)，B(,5)，所以AB(4,5)，选B． 2．设zabi，则abi2(abi)3i ，解得a 1,b1，故z 1i，对应的点在第四象限，选D． 3．含x2y的项为：C2x2( y)2 6x2y ，选C． 4 1 V 4．一斛米的体积为V  (2525022550)3652500 (cm3) ，一斗米的体积为 10500 (cm3)，选A． 3 5 3 2 2 b 5 5．sinA ，sinB ，则sinC sin(AB) ，故  ，又有bc2 10，所以b 5,c2 2 ， 10 2 5 c 2 2 3 5 bsinA 10 a   3，选B． sinB 2 2 6．取PF 中点M，则 FM b,OM a ，FP 2b, F P 2a，由双曲线定义可知 1 1 1 2 b b FP  F P 2a，所以2b4a，即 2，e 1( )2  5 ，选C． 1 2 a a 2 2 7．设abd，cbd ，abcb(b2 d2)2，所以d2 b2  (b0)，构造函数 f(b)b2  ， b b 2(b3 1) f(b) ，当b(,1)时， f(b)单调递减，当b(1,0)时， f(b)单调递增，所以 f(b)的最 b2 小值为 f(1)3，d2[3,)，d(, 3][ 3,) ，选A． y2 y 2   (y y )2 8．设点A( 1 ,y ),B( 2 ,y )，则OAOB 1 2  y y 4，设l:xmyt ，联立直线与抛物线方程得 1 2 1 2 4 4 16   y2 4my4t 0，y y 4t ，所以OAOBt24t 4，解得t 2，所以直线l与x轴的交点为P(2,0)， 1 2 O,D关于l对称，所以 OP  DP 2，D的轨迹方程为：(x2)2  y2 4，所以 DF r PF 1， DF r PF 3， DF (1,3]，选B． 高三数学参考答案 第 1 页（共 6 页） {#{QQABQY6AogioAIBAARgCAwGyCEMQkBAACIoOxBAEoAAACBFABAA=}#}二、选择题：本大题共3小题，每小题6分，共18分。在每小题给出的四个选项中，有多项符合题目要 求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 题号 9 10 11 答案 AB ACD BCD     2    2 2 2     9．(ab)a a ab110，A对； ab  a  b 2ab1427， ab  7 ，B对；  2 2 2      2ab 4 a  b 4ab44412 ， 2ab 2 3 ， 2b 4，C错；   1 a在b上的投影向量为 b，D错；综上答案为AB． 4    10．2时， f(x )cos2x ，因为cos2(x)cos(2x)cos2x ，所以 f(x )关于x 对称，A 6 6 2    4   1 对；2时，由0 x 可得 2x  ，此时cos(2x )的最大值为cos  ，B错； 2 3 3 3 3 3 2     若 f( )0，则   k,kZ，所以16k,kZ，且0，所以的最小值为1，C 6 6 3 2    2   对；因为 f(x)在( , )上单调递减，所以  ,  ，所以01，D对； 3 3 6 3 3 3 综上答案为ACD． 11．令x1,y0，则 f(1) f(1) f(0) f(1)f(0) ，代入 f(1)1得2f(0)0，即 f(0)0，A错； 由 f(0)0可得0 f(x) f(x) f(x)f(x) ，若存在x使得 f(x)1，则上式变为01，显然不成 x x x x x 立，所以 f(x)1，又 f(x)  f(  )  2f( ) f 2( )[f( )1]2 1，所以 f(x)1， 2 2 2 2 2 将0 f(x) f(x) f(x)f(x) 整理为 f(x)(1 f(x))f(x)， 由于1 f(x)0，所以 f(x)f(x)0，B对； f(x) f(x) f(x) 2(f(x) f(x) f(x)f(x)) 令g(x) ，则g(x)g(x)   0 ， f(x)2 f(x)2 f(x)2 (f(x)2)(f(x)2) 所以g(x)为奇函数，C对； f(n1)1 当nN*时， f(n1) f(n) f(1) f(n)f(1)2f(n)1， 2， f(n)1 所以{f(n)}为首项是2，公比为2的等比数列，所以 f(n)12n， n x n n n 由 f(x)1[f( )1]2可知(f( )1)2 2n，因为 f( )1，所以 f( )22 1(nN*)， 2 2 2 2 5 2k1 5 2k1 2(125) 11 11 所以 f( ) (2 2 1) 522  2 522 ，D对；综上答案为BCD． 2 12 k1 k1 高三数学参考答案 第 2 页（共 6 页） {#{QQABQY6AogioAIBAARgCAwGyCEMQkBAACIoOxBAEoAAACBFABAA=}#}三、填空题：本大题共3小题，每小题5分，共15分。 5 7 21 12． 13． 14． 3 9 7 567789 (57)2 (67)2 (87)2 (97)2 5 12．x  =7，s2   ． 6 6 3 sin 1 7 13．由题意得8 3cos，8sin3(1sin2) ，解得sin ，所以cos212sin2 ． cos 3 9 14．方法一：因为MN∥平面ABD，由线面平行性质定理可知MN∥IF ， IM AI m 设AI m(0m2)，因为EA平分BAC，所以   ， MC AC 2 MN MC 2  所以   ，又IF  m2 12mcos  m2 m1， IF IC m2 3 2 2 m2 m1 所以MN  IF  ，令m2t，t（2,4]，则 m2 m2 1 1 21 1 5 4 21 MN 2 7( )25( )1 ，当  ，即m 时MN 有最小值 ． t t 7 t 14 5 7 方法二：过点M 作MG∥AB交AC 于点G，连接GN ，由题意得GN∥AD，  所以MGN BAD ，设MGm(0m1)， 3 GN 2m 2m 则MG AGm，  ，所以GN  ， AF 2 2 1 7 4 3 4 21 所以MN  MG2GN22MGGN  (m )2 ，当m 时，MN 有最小值 ． 2 4 7 7 7 7 四、解答题：本大题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（13分） 解 （1）因为{a }为等差数列，由S 49，得a 7或a 3d 7， ...............2分 n 7 4 1 由a 2 a a ，得(7d)2 (72d)(710d) 或(a 4d)2 (a d)(a 13d) ， ...............4分 5 2 14 1 1 1 化简(7d)2 (72d)(710d) 得d2 2d 0，因为d 0，所以d 2． 所以a a (n4)d 2n1（nN*）． ...............6分 n 4 （2）由a 2n1知a 1,a 5，又{a b }为公比是3的等比数列， n 1 3 n n 所以a b (a b )9，即a b 3， ...............8分 3 3 1 1 1 1 所以a b 33n13n，b 3n (2n1)， .............10分 n n n 3(13n) (12n1)n 3n13 所以T    n2． .............13分 n 13 2 2 高三数学参考答案 第 3 页（共 6 页） {#{QQABQY6AogioAIBAARgCAwGyCEMQkBAACIoOxBAEoAAACBFABAA=}#}16．（15分） C1A3 18 3 A3 3 解 （1）记事件“1号球不在1号盒中”为A，则P(A) 3 3   或1 3  ． .................4分 A4 24 4 A4 4 4 4 （2）X 的取值为0,1,2,4，且X Y 4， 9 3 8 1 C2 1 1 1 P(X 0)  ；P(X 1)  ；P(X 2) 4  ，P(X 4)  ， ...............8分 A4 8 A4 3 A4 4 A4 24 4 4 4 4 3 1 1 1 所以E(X)0 1 2 4 1，E(Y)E(4X)4E(X)3， .............12分 8 3 4 24 3 1 5 1 X 0和4时XY 0，P(XY 0)   ，X 1时XY 3，P(XY 3) ， 8 24 12 3 1 5 1 1 X 2时XY 2，P(XY 4) ，E(XY)0 3 4 2 ， 4 12 3 4 所以E(X)E(Y)E(XY)． .............15分 （2）的解法二：Y 4X ，则E(Y)4E(X) ， ...............6分 E(X)E(Y)E(X)(4E(X))4E(X)(E(X))2， ...............8分 又E(XY)E(X(4X))E(4X X 2)4E(X)E(X 2) ， .............12分 所以E(X)E(Y)E(XY) E(X2)(E(X))2 D(X)， 由题意可知D(X)0，故E(X)E(Y)E(XY) 成立． .............15分 17．（15分） 解 （1）因为平面AEC 平面ABCD，且平面AEC平面ABCD AC ， BD AC，BD平面ABCD， 所以BD平面AEC，所以BD AE， ...............4分 又因为AP AB，E为PB中点，所以AE PB，又PBBDB， 所以AE 平面PBD． ...............6分 （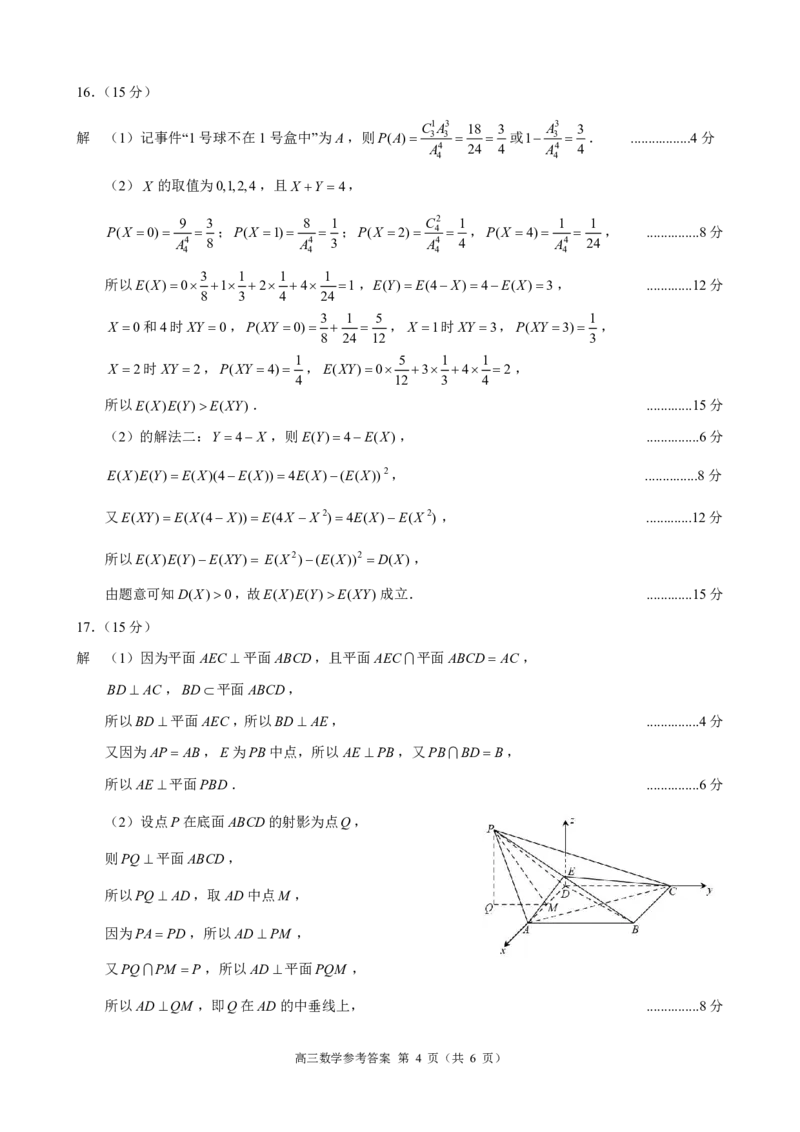2）设点P在底面ABCD的射影为点Q， 则PQ平面ABCD， 所以PQ AD，取AD中点M ， 因为PAPD，所以ADPM ， 又PQPM P，所以AD平面PQM ， 所以ADQM ，即Q在AD的中垂线上， ...............8分 高三数学参考答案 第 4 页（共 6 页） {#{QQABQY6AogioAIBAARgCAwGyCEMQkBAACIoOxBAEoAAACBFABAA=}#}如图建立空间直角建系，不妨取AB2，则设P为(1,a,b)，a2 b2 3，A(2,0,0)，B(2,2,0)， 3 a2 b  1 a2 b  所以E( , , )，AE ( , , )，DB(2,2,0)， 2 2 2 2 2 2   由（1）可知AEDB0，计算得a1，b 2 ，所以P(1,1, 2)， .............12分    又CB(2,0,0)，CP(1,3, 2)，设平面PBC 的法向量为m(x,y,z)，则   mCB0 2x0    ，即 ，取m(0, 2,3)， mCP0 3y 2z0   22 所以sin cos AB,m  ． .............15分 11 18．（17分） 解 （1）因为 f(x)aax (axb)axlna ， f(0)e ablnae 所以 ，即 ，所以ae，b0． ...............6分 f(0)0 b0 （2）当b1时， f(x)[(alna)xlnaa]ax， 因为 f(x)存在极小值点，所以alna0，解得a1， ...............8分 lnaa lnaa lnaa lna 1 此时x  ，所以x lna ，即lnax 0  ，ax 0 e a ， 0 0 alna a a lnaa lna 1 a ( lna 1) 所以 f(x )(ax 1)ax 0 (a 1)e a ( )e a ， 0 0 alna lna lna et1 令t g(a) ，则 f(x ) h(t) ， .............12分 0 a t 1lna 因为g(a) ，所以当1ae时，g(a)单调递增，当ae时，g(a)单调递减， a2 1 1 又a1时，lna0，所以g(a)0，所以0 g(a) g(e) ，即0t ， .............15分 e e (1t)et1 1 1 1 因为h(t) ，所以当t(0, ]时，h(t)单调递增，所以h(t)h( )ee． .............17分 t2 e e 高三数学参考答案 第 5 页（共 6 页） {#{QQABQY6AogioAIBAARgCAwGyCEMQkBAACIoOxBAEoAAACBFABAA=}#}19．（17分） 7 解 （1）取C 上任意一点为A(x,y)(x0,y 0)，经过( )变换后得到C 上的对应点为B(x,y)， 0 1 4  2  2 x (x y) x (x y) 7  2  2 由题意可知( )为： ，变形后得 ， ...............4分 4  2  2 y (x y) y (x y)    2  2 2 2 2 即A( (xy), (xy)) ，将点A的坐标代入C 的方程得x2 y2 3，x (x y)0， 0 2 2 2 所以C 的方程为：x2 y2 3(x0)． ...............6分 1 （2）因为C ,C 均经过点(2,1)，所以(2,1)为它们的公共点， 1 2 所以不妨取M(2,1),N(2,1)，则l :x2y，l :x2y， ...............8分 OM ON x 2 y 2 x 2 设C 上的动点P为(x ,y )，则有 0  0 1，移项得y 2 b2(1 0 )，记为（i）式， 2 0 0 a2 b2 0 a2 4 1 又因为C 过点M(2,1)，所以  1，记为（ii）式， ...............10分 2 a2 b2  1 y y  (xx ) x 2y x 2y x 2y x 2y 联立 0 2 0 得x 0 0 ,y 0 0 ，所以H( 0 0, 0 0)，  x2y 2 4 2 4 x 2y x 2y x 同理得G( 0 0, 0 0) ，则 GH 2 (2y )2( 0)2， ...............12分 0 2 4 2 4 记直线OM 与直线ON 的夹角为，计算得sin ， 5 GH 5 x 由题意可知 2r b，所以 GH 为定值2b，所以 GH 2 (2y )2( 0)2 4b2 ，记为（iii）式， sin 2 0 2 x 2 x a2 16b2 将（i）式代入（iii）式得4b2(1 0 )( 0)2 4b2，即x 2( )0恒成立， a2 2 0 4a2 5 所以a4b，与（ii）式联立解得a2 5，b ， ...............14分 2 5 S 2S  x y x y  4y 0 2 x 0 2  5 4 x 0 2 ，因为0 x 2 5，x  2， 四边形OGPH △OHG H G G H 4 4 0 0 5 5 x 2 4 0 所以0 5，四边形OGPH 面积的取值范围为(0,5]． ..............17分 4 高三数学参考答案 第 6 页（共 6 页） {#{QQABQY6AogioAIBAARgCAwGyCEMQkBAACIoOxBAEoAAACBFABAA=}#}